调洪演算解析解法
陈起红
(余姚市江河水利建筑设计有限公司,浙江 余姚 315400)
1 问题的提出
调洪演算在水利计算中广泛应用,由于水位、下泄流量、蓄水量三者之间存在非线性关系,不能直接求解,故一般用图解法、试算法等,随着计算机的应用,数值计算也较方便。但采用解析解法,用一般函数直接计算更方便。调洪演算是一阶常微分方程,如中间变量用水位或下泄流量,除了假定与成线性关系可以求解外,一般没有解析解。本文采用蓄水量为中间变量,通过假定是的一元两次方程关系,可以得出函数解。可在水库调洪演算或洪水预报中应用。
2 调洪演算解析解法
调洪演算计算方程如下:

式中:I为时段入库流量(m3/s);q为下泄流量(m3/s);w为蓄水量(m3);t为时间(s),若假设:

式中:a,b,c为系数。
把式(2)代入式(1)得:



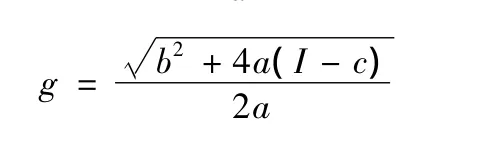

式中:w0为初始值,m3;t为计算时段长,s。
计算出w后,可由式(2)求得q,再推出库水位。
若t时段内q不连续,先算出至蓄水量w1的时间,可分为t=t1+t2,先算出至w1的时间。
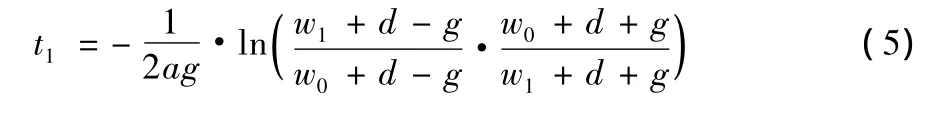
再由初始值w1及t2算出时段末的W。
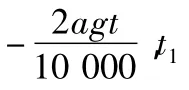
为建立q与w的一元二次方程,可用最小二乘法进行数值拟合。
令:M=∑[q-(aw2+bw+c)]2
根据以下方程式求出a,b,c:
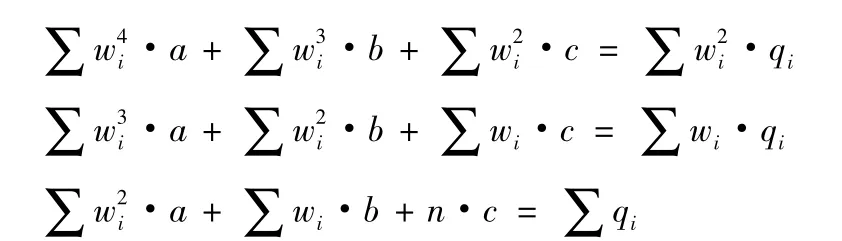
式中n为个数。
若下泄流量随水位有不同的运行方式或者为提高计算精度,可分段拟合。
3 算例
某水库堰顶高程59.98m,堰宽B=70m,M=1.77。不同水位的水库库容曲线及下泄流量见表1。

表1 不同水位蓄水量和下泄流量表
分2种方案,方案1采用库水位59.98~63.50m整段拟合,方案2采用59.98~61.50m和61.5~63.50m两段拟合。各个方案计算成果见表2。
调洪计算成果见表3。

表2 各方案系数表

表3 各方案调洪演算成果表
从以上分析看,采用解析解法与数值计算的成果比较接近。
4 结语
调洪演算为一阶常微分方程,通过采用中间变量 (蓄水量),假设与非线性关系为一元二次方程,实际是求解黎卡提 (Riccati)方程,若时段内入库流量为常量时,有函数解,可直接求出计算结果。此计算方法可在水库调洪演算和洪水预报中应用。
[1]吴王城.工程水文学[M].北京:水利电力出版社,1985.
[2]周义仑,靳祯,秦军林.常微分方程及其应用[M].北京:科学出版社,2013.
[3]同济大学数学教研室.高等数学 [M].北京:高等教育出版社,1989.

