拟合法和平差法在点云中建立物体曲面的比较
段存宏
(中国人民解放军 61175部队,山东 淄博 255000)
拟合法和平差法在点云中建立物体曲面的比较
段存宏
(中国人民解放军 61175部队,山东 淄博 255000)
使用3D激光扫描仪的目的是获取物体的表面形状.现在大多使用拟合的方法对点云数据进行处理来建立曲面.以约束球为例对以最小二乘为准则的拟合法和平差法进行了讨论,拟合法虽然有一定的优点,但同时也存在不能对数据进行精度评定的不足,而平差法正好弥补了这一缺陷.除此之外,平差法还可求出参数的点位中误差,进而可画出误差椭球,丰富了点云数据的处理过程,使点云数据的处理结果趋于形象化,为点云处理提供了新的思路.
拟合法;平差法;物体曲面;点云处理
高速3D激光扫描仪和拥有持续扫描探测坐标的测量仪正在更多的应用到采集物体表面点数据的实践中.由于这些点数据具有很高的密度,所以通常被称作点云[1].利用空间三维点云数据建立曲面有许多可行的算法,这些算法包括Hoppe的水平集算法[2],Bernardini的球旋转算法,Amenta的外壳算法[3]等.在测量中一般使用曲面拟合法,对点云数据自由参数的曲面拟合是计算机辅助设计和计算机制图中遇到的基本问题[4].
一般的曲线和曲面的拟合方法的目的是通过点云得到一个近似的物体表面形状[5],没有进行结果的精度评定.在测量中,对测量结果进行精度评定是重要的一步,它可以直观的表现出测量结果的好坏以及是否达到工程要求.通过基于多因素决定的最小二乘准则,通常能得到关于结果精度和准确性的可靠信息[6].以最小二乘为准则的拟合法能够把误差的影响降到最小,但这种方法存在着许多不足之处.拟合法采用的是多项式,如果待求参数存在非独立项,则参数之间只有满足相应的关系才能得到预期的拟合面,而拟合没有对相关项的约束;观测值是带有误差的,拟合没有考虑观测值误差的影响.平差法是依据最小二乘准则,由一系列带有观测误差的测量数据来求定未知量的最佳估值及精度.本研究以约束球为例对拟合法与附有参数的条件平差法进行了比较,得到了比较严谨的结论.文中把半径已知的球称为约束球,半径未知的球称为自由球.
1 球面拟合原理

根据文献[8],用X={Xi,i=1,…,m}表示一系列形成目标曲面的数据点,用S(u,v,P)表示B样条曲面,其中P={P0,…,Pn}为曲面S(u,v,P)的控制点,u,v为曲面S(u,v,P)的参数.拟合的准则为
(1)
式中d(S,Xi)是Xi到S(u,v)的垂直距离,d(S,Xi)=‖Xi-S(ui,vi)‖,fs是P的一个二次函数.
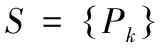
(u,v,w)为球心坐标,r为球的半径,k点应满足方程:
(2)
展开式(2),两边同除-(u2+v2+w2-r2),并用A,B,C,D表示系数得到
(3)
由A,B,C,D计算u,v,w,r公式为
(4)
根据上述拟合原理用EEXLT程序(平台为IDL语言)对点云数据进行处理,得到约束球未知参数u,v,w,r的值.
2 约束球的三个位置特征参数确定
在扫描点的过程中,只能得到物体表面的点的数据.在将规则物体作为标靶时,往往需要确定该物体的其他参数.因此,把该参数作为未知参数参与平差过程,这就是在测量工作中经常用到的附有未知参数的条件平差.
平差的数学模型为
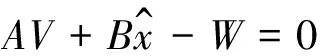
(5)

依据最小二乘准则min= VTV最终可得
(6)
(7)


(8)
(9)
式中
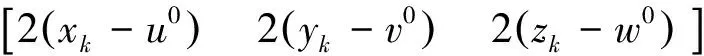
(10)
(11)
(12)

对于n(n>4)个点组成方程
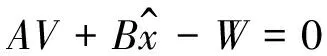
(13)
系数阵A的形式为
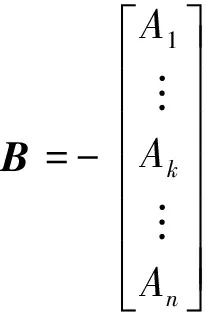
其中•表示1×3的0矩阵,球心坐标和点云三维坐标的改正数可由公式(6)、(7)得到,所以约束球的三个位置特征参数得到确定.
球心坐标的点位中误差公式为
(14)
式中Quu、Qvv、Qww可由

根据Cardan解法可以求出误差椭球的三个特征值,进而可以求出主轴向量画出误差椭球来形象表示圆心坐标在各个方向上的误差.
3 实验分析
3.1 实验数据
本实验数据是由3D激光扫描仪得到的四组球面测量数据,在进行本实验前须先对扫描数据进行剔除粗差很大的噪声点的预处理工作.
3.2 参数结果对比及分析
通过用EEXLT程序(平台为IDL语言)对数据分别进行处理,完成约束球的拟合与平差过程,得到的参数差值(平差参数值-拟合参数值)见表1.
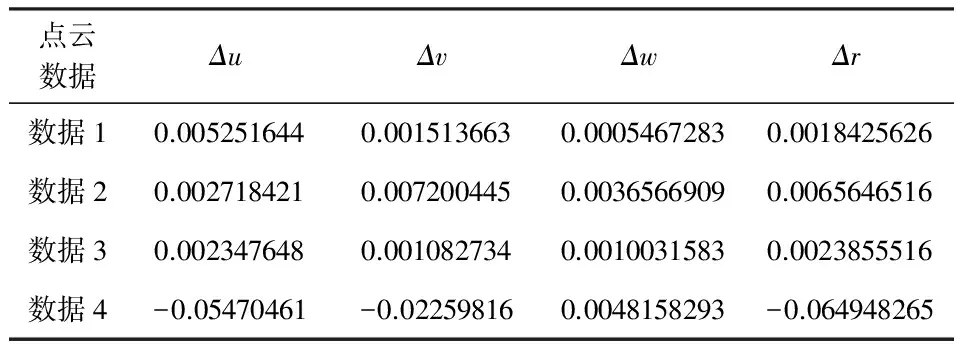
表1 3D激光扫描数据差值表 m
从数据差值表中可以看出拟合得到的约束球的四参数与平差得到的相差不大.原因是在进行实验前对数据进行了大量的预处理工作,除去了误差大的点,使用的是数据误差都比较小.
3.3 平差法进行精度评定
使用拟合法无法对参数结果进行精度评定,而平差法可以.使用平差法时可用中误差σ做为评定精度指标,但前提是数据只存在偶然误差,而在实际测量过程中还存在着系统误差和粗差,所以需要验证该实验数据是否大致符合偶然误差的四个性质.将点在geomegic软件中打开,并且导入拟合球面数据将其封装得到图1~4.

图1 3D激光扫描数据1

图2 3D激光扫描数据2

图3 3D激光扫描数据3
图4 3D激光扫描数据4
由图可证实偶然误差的两个性质:在一定观测条件下,误差的绝对值有一定的限制;绝对值较小的误差比绝对值较大的误差出现的概率大.对于性质3(绝对值相等的正负误差出现的概率相等)和性质4(偶然误差的数学期望为0)可由表2(n1为拟合球面上的点,n2为拟合球面下的点数,N为总点数)看出,所以用中误差σ可以较好的地表示计算精度.
表2 3D激光扫描数据点数表

点云数据n1n2Nn1Nn2NE(Δ)数据1126862120.594339620.405660380.001815数据23935459380.418976550.58102345-0.00122数据32681524200.638095240.36190476-0.00073数据458721300.446153850.55384615-0.00637
使用拟合法和平差法都可对数据进行处理,处理结果由表1可以看出相差不大,但平差法可以对结果数据进行精度评定.可计算出球心坐标的点位中误差.
表3 参数的点位中误差

点云数据点位中误差点云数据点位中误差数据10.0000075数据30.00000147数据20.00000132数据40.00000242
引用Cardan解法可以得到结果数据的误差椭球,可以看出圆心坐标在各个方向上的误差,为了形象展示立体效果,用geomagic封装,如图5~8所示.

图5 数据1处理结果的误差椭球
图6 数据2处理结果的误差椭球

图7 数据3处理结果的误差椭球

图8 数据4处理结果的误差椭球
4 结论
通过理论分析与实验证明可得到以下结论:
1) 在测量数据存在较小系统误差的情况下,通过拟合方法得到的结果与平差得到的相当;在测量数据存在较大系统误差的情况下,拟合法得到的结果比平差法得到的要精确一些.
2) 平差方法具有拟合法所不具备的一些特征.由平差法可求出参数的点位中误差,进而可画出误差椭球,丰富了点云数据的处理过程,使点云数据的处理结果趋于形象化.
3) 在实际的测量过程中系统误差不可避免的会出现,这对使用平差法有一定的影响,所以在使用平差法前要对数据进行更加精确的预处理.
[1]DaoS,OuY.Onthenormalvectorestimationforpointclouddatafromsmoothsurfaces[J].Computer-AidedDesign(PEG),2005, 3 (7) :1071-1079.
[2] 张睿智. 结合模糊理论的灰度不均匀图像水平集分割算法研究[D]. 南京: 南京理工大学,2014.
[3] 牛玉美. 基于CUDA的可视外壳并行计算方法研究[D].青岛:中国石油大学,2011.
[4]PengBB,WenP,WangA.Arevisittofittingparametricsurfacestopointclouds[J].Computers&Graphics(PEG),2012,36(1):534-540.
[5]SimonF,Fittingcurvesandsurfacestopointcloudsinthepresenceofobstacles[J],ComputerAidedGeometricDesign.(PEG),2009,26(1): 192-202.
[6] 潘国荣, 房鹤飞, 唐杭. 基于等效全最小二乘准则的稳健球面拟合方法[J].测绘通报, 2013,S1:99-102.
(编辑:刘宝江)
The comparison research of fitting and the compensation oferrors in setting the object surface in the point cloud
DUAN Cun-hong
(61175 Troops,The Chinese People′s Liberation Army,Zibo 255000,China)
The purpose of using a 3D laser scanner is to obtain the shape of the object surface. Now the fitting method is mostly used to process point cloud data to create the surface. In this study, we took the restraint ball as an example, and developed the scientific and deeply discussion on fitting method and the compensation of errors, based on the rule of the least squares. Although there are certain advantages of the fitting method, it can’t give the accuracy judgement of the data at the same time. However, the compensation of errors make up the disadvantage. Besides, the second method can also make out the point error of the parameters, then draw out the error ellipsoid. It enriches the process of point cloud data, make the processing result of point cloud data tend to be visualized, and provides a new way of thinking for point cloud processing.
fitting; the compensation of errors; the object surface; point cloud processing
2015-01-30
段存宏, 男, 275503036@qq.com
1672-6197(2015)06-0039-04
P
A

