跑步机上行走与平地行走膝关节运动差异性研究

赵凌燕，黄守刚，隋立明，李金

(哈尔滨工程大学 机电工程学院, 黑龙江 哈尔滨 150001)

跑步机上行走与平地行走膝关节运动差异性研究

赵凌燕，黄守刚，隋立明，李金

(哈尔滨工程大学 机电工程学院, 黑龙江 哈尔滨 150001)

为了解人在跑步机上行走与在地面行走的差异性，基于多元信息融合算法，通过对20名健康男性青年在平地行走和跑步机上行走时膝关节转角及步态相位的数据对比分析，发现了二者之间的共性和差异性，并对曲线进行了模型分析，结果表明在跑步机上行走较在平地行走稳定性差，膝关节转角波动范围是平地上行走的2～3倍以上。为了保证跑步机上行走的平稳性，人主观上通过使摆动腿提前着地，减小摆动时间，从而增加双脚同时与跑台的接触时间来保持行走的平衡性和稳定性，摆动腿着地时刻的膝关节弯曲角度明显大于平地上行走。Gauss扩展函数只适合于对平地行走时膝关节的转角曲线进行模型分析，跑步机上行走时膝关节转角曲线可采用Fourier函数建立数学模型。以上结论在康复器械、宇航员训练和体育研究领域具有一定的应用价值。

膝关节转角；相位；跑步机；步态；数学模型

近年来，国内外相关机构在人体运动生物学领域进行了大量的科学研究，其中有关步态特征的研究方法往往基于跑步机平台进行测量实验，将实验数据作为人体正常步态数据进行科学研究[1-4]。然而人在跑步机上的步态与人在平地上的步态是否具有完全一致性的问题，到目前为止国内外仍没有较深入的研究成果[5-7]。从客观上分析跑步机上行走与平地行走的区别主要表现为以下几个方面：1)平地行走时与足底的接触物，即地面是绝对静止的，而跑步机上行走时跑台是以恒定速度运动的；2)平地行走时行走方向、速度、加速度受人主观意识控制，而在跑步机上行走时行走方向、速度、加速度受跑步机被动约束，不可以主观控制；3)平地行走时，周围景物相对人的运动速度与行走速度大小相等，方向相反，可以依靠视觉反馈来判断行走速度，而在跑步机上行走时周围景物与人相对静止，人只能依靠肢体的运动感知行走速度。由于存在以上客观条件的不同，本文针对人在跑步机上行走与平地行走时膝关节转角及步态相位特征的差异这一问题展开如下研究。

1 研究方法

本文采用多样本实验测量的方法对跑步机上行走与平地行走时膝关节转角及步态相位进行分析。选用加拿大NEODYN公司开发的穿戴式实时无线传感动作捕捉及力学评估系统(functional assessment of biomechanics system，FAB)和无线步态相位检测系统，通过采用多元信息融合算法进行人体动态动作捕捉，其特点是精度高，体积小，穿戴方便，数据通过无线传输，可进行室内外长距离行走下的不间断数据采集。

一个完整的步态周期是指从一侧足跟着地到该足跟再次着地，由支撑相和摆动相构成，支撑相是指脚与地面相接触的时期，双脚同时着地的时期称为双支撑期，只有一只脚着地的时期称为单支撑期；摆动相为脚离开地面的时期，时间上与另一只脚的单支撑期相同。本文的研究均以人体下肢的右侧系统为参考，即右足跟着地时刻为步态周期的起始时刻[8]。

膝关节的屈伸是指膝关节沿冠状轴的运动，按照国际惯例膝关节转角定义为小腿相对于同侧大腿沿冠状轴向身体后侧旋转的角度[9]，如图1所示，qk即为膝关节转角。

图1 膝关节转角示意图Fig. 1 Schematic diagram of knee joint angle

2 数据处理及特征分析

选择20名健康男性青年作为实验对象，身高在165～185cm，无体重限制。测试者首先在平地上沿直线以自然速度行走，有效时间为2min，然后让测试者在跑步机上以主观感觉最接近平地行走状态的速度行走，记录行走速度，有效行走时间仍为2min。测试者在实验之前需进行必要的跑步机行走训练，以避免不适应所造成的误差。

2.1 膝关节转角数据对比及特征分析

图2所示为随机抽取11个样本对象在平地行走和跑步机上行走的膝关节转角的原始曲线。观察曲线特征可知，人在跑步机上行走与在平地行走时膝关节的转角变化规律既有相似性，又有差异性。

图2 多样本膝关节转角原始曲线Fig. 2 Original curves of multiple samples' knee joint angle

相似性主要表现在转角曲线都有2个波峰，前波峰幅值明显小于后波峰幅值，单个波峰出现在步态周期的相位位置大致相同、幅值相似。差异性主要表现在步态周期起始时刻，跑步机上的膝关节转角明显比平地上的转角大。

图3为随机抽取6个样本对象在有效采样时间内取100个步态周期的膝关节转角曲线。由图观察可知：跑步机上行走时膝关节的转角分布相对分散，即幅值和相位变化范围都明显大于平地行走时膝关节转角曲线。

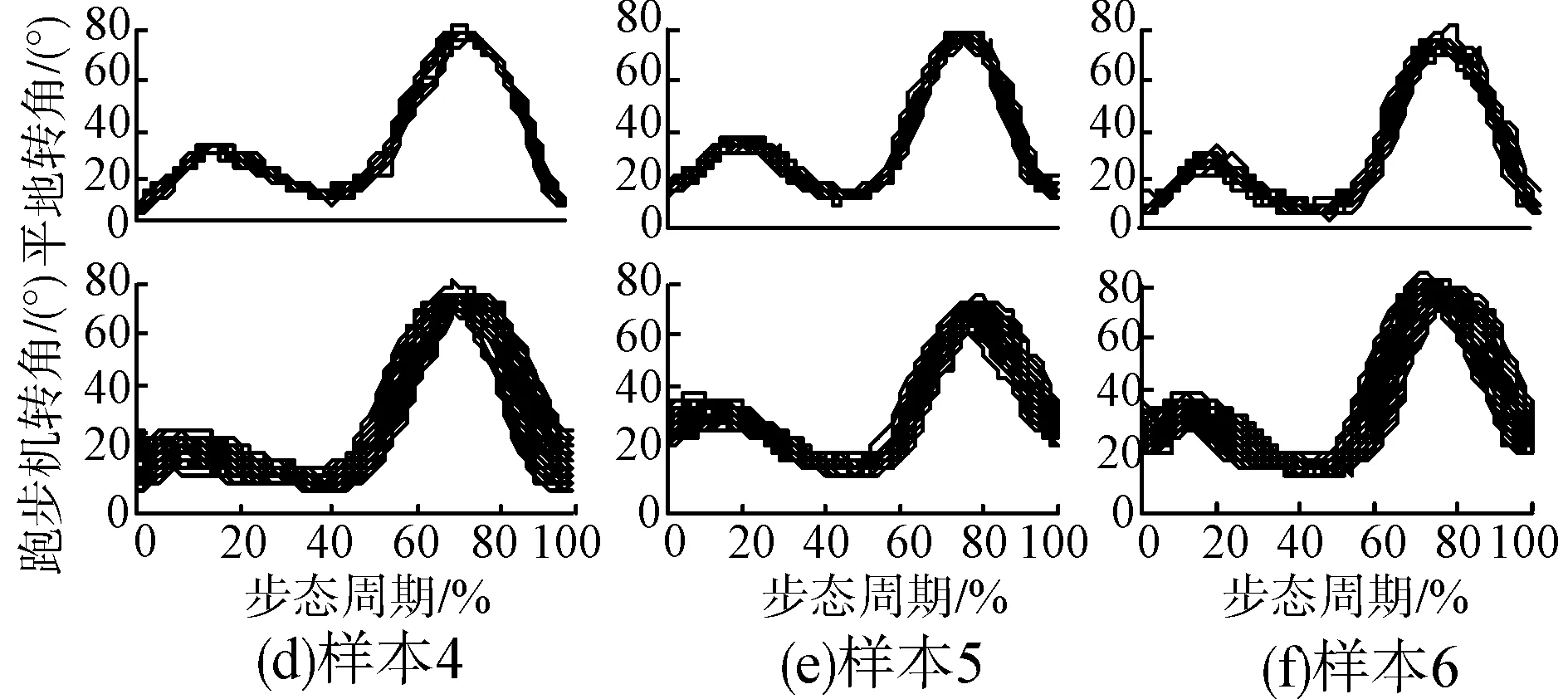
图3 6个样本的膝关节转角对比曲线

(1)

(2)

表1给出了跑步机上行走与平地行走时膝关节的转角幅值波动范围(wT、wG)以及标准差(ST、SG)。由此可知：人在跑步机上行走时膝关节的转角幅值波动范围是平地行走时的2～3倍以上，标准差是平地行走时的1.38～2.87倍。

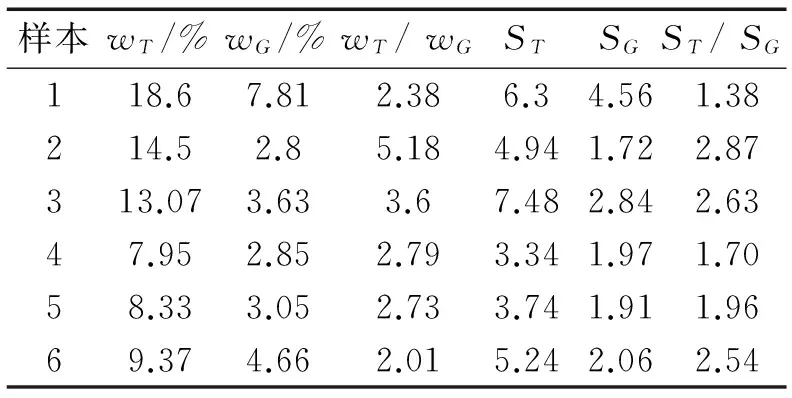
表1 膝关节转角波动范围及标准差

对图3所示的每100条曲线数据加权平均得膝关节转角平均曲线如图4所示。由图观察可知每个样本的平均曲线均有一个显著特征：在步态起始时刻，跑步机上行走时膝关节的转角明显大于平地行走时膝关节的转角。此特征表明：在跑步机上行走时的足跟着地时刻，小腿相对大腿向后弯曲程度较平地行走时大，小腿没能完全伸直，此特征是否会对步态有影响，将在后续工作中给予研究和证实。

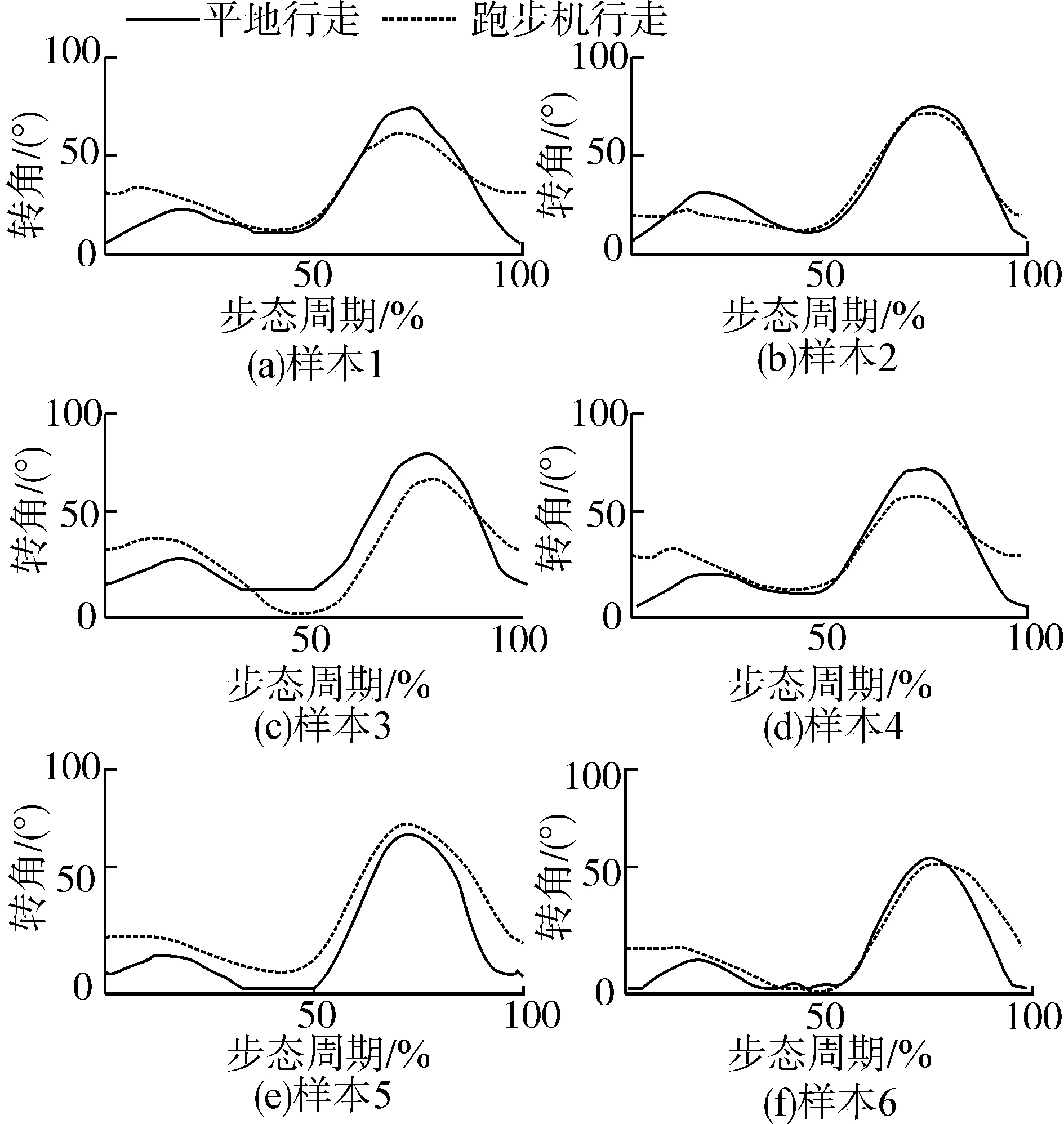
图4 6个样本的膝关节转角平均曲线Fig. 4 Average curve of 6 samples' knee joint angle

2.2 步态相位数据对比及特征分析

图5所示为随机抽取的一个样本在平地上行走和跑步机上行走的100个步态周期内足跟、足趾与接触面的接触状态，“0”表示接触，“1”表示离开。

图5 足跟、足趾与接触面接触状态Fig. 5 Contact state between heel, toes and contact surface

图6为加权平均后的曲线。t0为右足跟着地时刻，也是步态周期的起始时刻，t1为左足趾离地时刻，t2为右足趾着地时刻，t3为右足跟离地时刻，t4为左足跟着地时刻，t5为右足趾离地时刻，t6为左足趾着地时刻，t7为左足跟离地时刻，t'0为右足跟再次着地时刻，即为下个步态周期的起始时刻。由图6可知，该样本在平地和跑步机上行走时，足跟与接触面的接触状态无明显差异，而足趾与接触面的接触状态有明显差异：1)跑步机上行走时t1和t5时刻较平地行走向后推移，即跑步机上足趾离地时刻滞后与平地行走；2)跑步机上行走时t2和t6时刻明显超前于平地行走的t2和t6时刻，即跑步机上行走时，足趾紧随同侧足跟着地而着地。

图7所示为该样本的步态相位饼图，由图可知，跑步机上t2已经超前于t1，t6已经超前于t5，已经不再符合正常人的步态时序[9]。

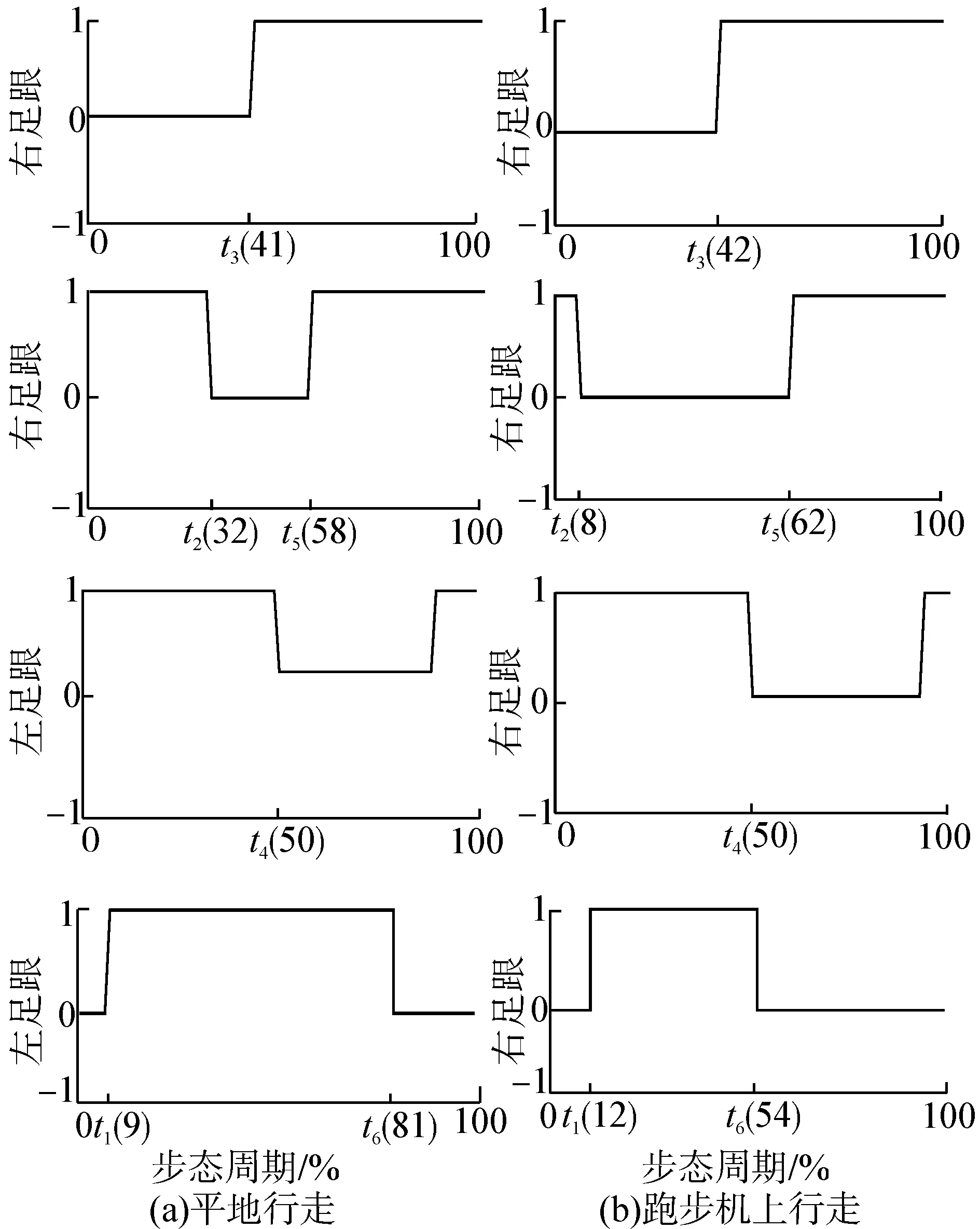
图6 足跟、足趾与接触面接触状态平均曲线Fig. 6 Average curve of contact state between heel, toes and contact surface

为了验证以上结论是否具有普遍性意义，表2给出了随机挑选的6个样本分别在跑步机上和平地上行走时的相位数据，下脚标T表示跑步机上行走的数据，G表示平地行走的数据，PSL为左侧下肢摆动期，PSR为右侧下肢摆动期。由表中数据可知：在跑步机上行走时6个样本左、右侧下肢的摆动期均比平地行走的摆动期小2%～5%，左右足趾着地时刻(t6_T、t2_T)明显超前于平地行走的足趾着地时刻(t6_G、t2_G)。由此可见，样本为了适应跑步机环境，本能的减小了单侧下肢的摆动期时间，进而增加了双支撑期时间。

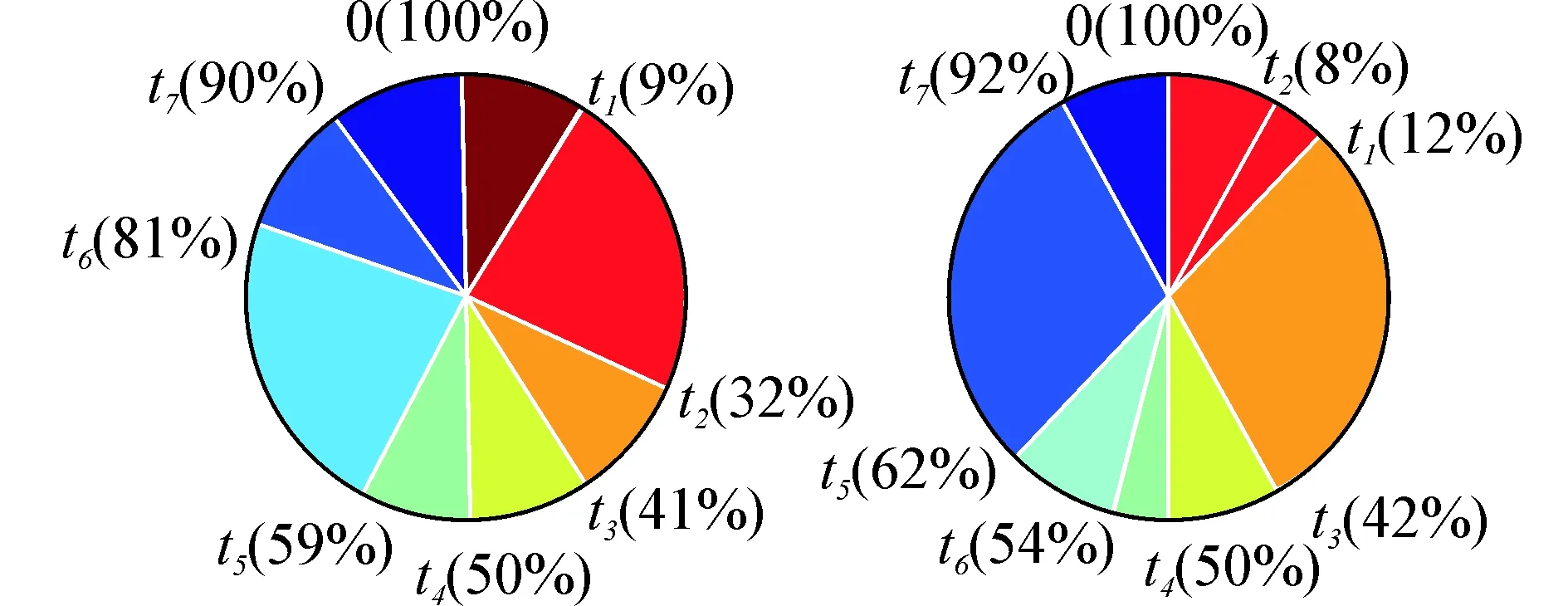
图7 相位饼图Fig. 7 Pie chart of phase

表2 6个样本在跑步机上和平地行走时的相位

3 膝关节转角数学模型分析

由上文分析可知，人在平地行走和跑步机上行走的膝关节转角曲线均为双峰曲线，本文采用Gauss扩展函数对其建模，如下：

(3)

式中：自变量t为步态周期百分比，a1、b1、c1、a2、b2、c2为拟合系数。

对图4中的6组平地行走时膝关节转角原始数据和6组跑步机上行走时膝关节转角原始数据分别采用上式进行曲线拟合，结果如图8和图9所示。拟合标准差及拟合优度如表3所示，其中SG、RG为平地行走的标准差及校正后的拟合优度，ST、RT为跑步机行走的标准差及校正后的拟合优度。

如图8和表3所示，用Gauss扩展函数模型拟合平地行走时膝关节转角曲线，标准差较小，拟合优度接近1，表明拟合曲线可以跟随并表征原始数据曲线变化特征，即可以采用Gauss扩展函数对平地行走膝关节转角曲线进行数学建模。

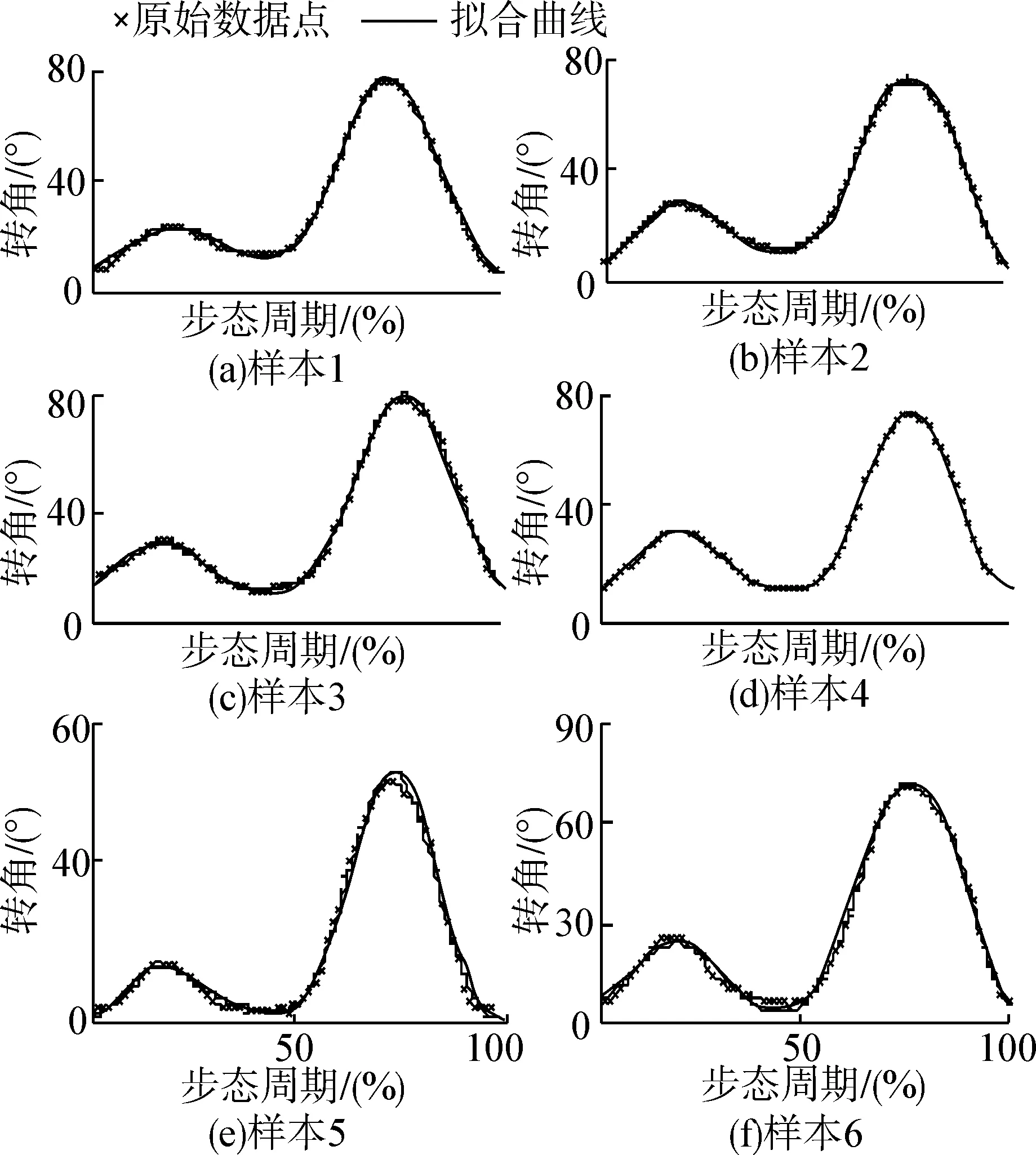
图8 平地行走膝关节转角Gauss函数拟合曲线Fig. 8 Gauss function fitting curve of the knee joint angle during walking on the ground

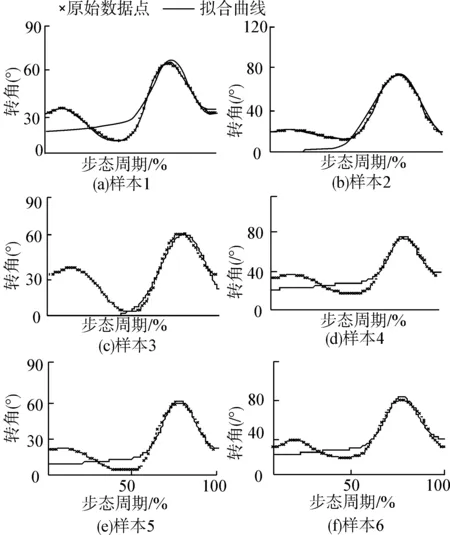
图9 跑步机上行走膝关节转角Gauss函数拟合曲线Fig. 9 Gauss function fitting curve of the knee joint angle during walking on a treadmill

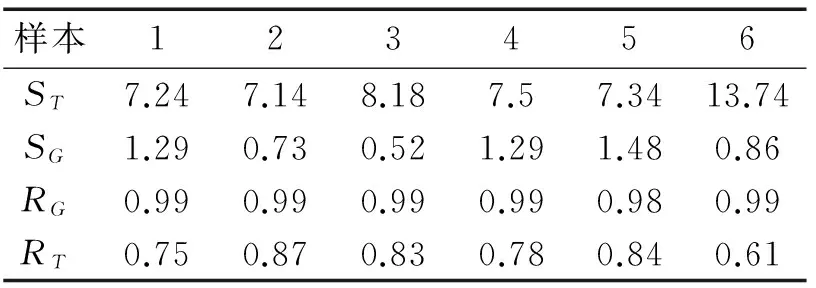
表3 Gauss函数模型拟合标准差及优度

如图9和表3所示，用式(3)所示函数对跑步机上行走时膝关节的转角曲线进行拟合，不仅标准差较大，而且拟合优度很小，第一个波峰处拟合曲线明显不能跟随原始数据曲线的变化，而第二个波峰拟合效果很好，说明用Gauss函数不能较好的表征跑步机上行走膝关节的转角变化特征。故采用Fourier函数扩展模型对跑步机上行走时膝关节的转角曲线进行拟合，如下：

f(t)=a0+a1cos(wt)+b1sin(wt)+a2cos(2wt)+

b2sin(2wt)+a3cos(3wt)+b3sin(3wt)

(4)

式中：自变量t为步态周期百分比，a0、a1、b1、a2、b2、a3、b3、ω为拟合系数。

对图4中6组跑步机上行走时膝关节转角原始数据采用式(4)进行曲线拟合，如图10。如表4，标准差较小，拟合优度接近1，表明拟合曲线可跟随并表征原始数据曲线变化特征，即可采用Fourier扩展函数对跑步机行走时膝关节转角曲线进行建模。

图10 跑步机上行走膝关节转角Fourier函数拟合曲线Fig. 10 Fourier function fitting curve of the knee joint angle during walking on treadmill

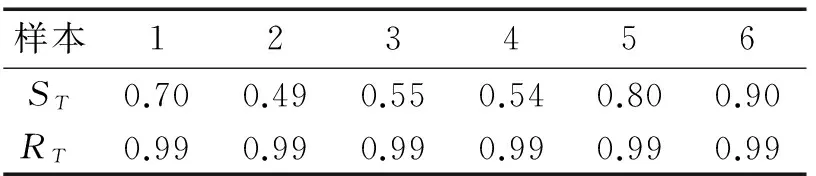
表4 Fourier函数拟合标准差及优度

4 结论

本文通过对多样本在平地行走和跑步机上行走时膝关节转角及步态相位的数据对比分析得到以下结论：

1)人在平地行走和在跑步机上行走时膝关节转角幅值和相位无明显差异性，但在跑步机上行走时膝关节转角稳定性较差，波动范围是平地行走的2～3倍以上；

2)人在跑步机上行走足跟着地时刻膝关节转角明显大于平地行走时，即：小腿没能完全向前伸直时足跟就已经着地；

3)跑步机上行走时，足趾着地时刻明显较平地行走时提前，即足跟着地和同侧足趾着地时间间隔明显变短；

4)跑步机上行走时摆动期，或单支撑期明显小于平地行走；

5)Gauss扩展函数模型只适用于平地行走膝关节转角曲线，采用Fourier函数可以对跑步机上行走时膝关节转角曲线进行数学建模。

以上结论表明，人在跑步机上行走较在平地行走稳定性差，为了保证行走的稳定性，人主观上通过使摆动腿提前着地，进而缩短摆动时间，增加双脚同时与跑台接触的时间来保持行走的平衡性和稳定性。这在康复评定、宇航员训练和体育研究领域具有一定的应用价值。

[1]宋雅伟, 孙文, 寇恒静. 步态运动学及动力学的研究方法[J]. 中国组织工程研究与临床康复, 2010, 14(3): 321-324. SONG Yawei, SUN Wen, KOU Hengjing. Research methods of gait kinematics and kinetics[J]. Journal of Clinical Rehabilitative Tissue Engineering Research, 2010, 14(3): 321-324.

[2]郑秀瑷. 现代运动生物力学[M]. 北京: 国防工业出版社, 2002: 79-81.

[3]张彦龙, 马志君, 于潇. 跑步机坡度与运动时膝关节力学关系分析[J]. 牡丹江师范学院学报:自然科学版,2011(1): 52-54.

[4]李建微, 李晓雯, 陈崇成. 跑步机平台下人体运动参数分析[J]. 现代计算机, 2012(7): 10-14. LI Jianwei, LI Xiaowen, CHEN Chongcheng. Analysis of sport parameters of human on running machine[J]. Modern Computer, 2012(7): 10-14.

[5]SALIM M S, MAKNOH F N, OMAR N, et al. A biomechanical analysis of walking and running on a treadmill in different level of inclined surfaces[C]//International Conference on Biomedical Engineering. Penang, 2012: 308-312.

[6]YABE Y, WATANABE H, TAGA G. Treadmill experience alters treadmill effects on perceived visual motion[J]. PLoS One, 2011, 6(7): e21642.

[7]LOVECCHIO N, GALANTE D, TURCI M, et al. Quantitative analysis of rotational movements of knee in healthy subjects during treadmill barefoot walking[J]. The Open Sports Medicine Journal, 2008, 2(1): 28-33.

[8]郭险锋. 步态分析[EB/OL]. (2007-06). http://wenku.baidu.com/view/7ecfd659312b3169a451a425.html.

[9]王令军. 康复机器人样机研制及步态控制研究[D]. 哈尔滨: 哈尔滨工程大学, 2010: 17-19. WANG Lingjun. Research on rehabilitative robot prototype and gait control[D]. Harbin: Harbin Engineering University, 2010: 17-19.

Differences between knee movements
walking on flat ground and on a treadmill

ZHAO Lingyan，HUANG Shougang，SUI Liming，LI Jin

(School of Mechanical and Electrical Engineering, Harbin Engineering University, Harbin 150001, China)

To examine the difference between walking on the ground and on a treadmill, the knee joint angle and gait phases of 20 healthy men were analyzed by multi-information fusion algorithm, then the similarities and differences between walking on the ground and the treadmill were discovered. Model analysis of the curves were conducted showing that walking on a treadmill has less stability than walking on the ground, and the fluctuation range of the knee joint angle is 2 to 3 times more than walking on flat ground. In order to ensure stable walking on a treadmill, the experimentees put their swinging feet down ahead of time, reducing the swing time, so the contact time between their feet and the treadmill was increased to keep balance and stability. The bending angle of knee joints when swinging feetland on the treadmill shows to be obviously larger than walking on the ground. Concluding, the Gauss expansion function is only suitable for model analysis of the knee joint angle curve while walking on flat ground. The knee joint angle curve while walking on a treadmill can better be mathematically modelled by Fourier function. This has design and application value in rehabilitation equipment, astronaut training, and sports research.

knee joint angle；phase；treadmill；gait；mathematical model;knee movement

2014-07-10.

时间：2015-07-27.

国家自然科学基金资助项目(61203358/F0306);中央高校基本科研业务费专项资金资助项目(HEUCF150703).

赵凌燕(1981-),女，讲师，博士.

赵凌燕, E-mail：zly6668837@163.com.

10.3969/jheu.201407026

TP272

A

1006-7043(2015)09-1259-05

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.U.20150727.1143.001.html