非线性参数拟合的桥梁概率地震需求模型研究

袁万城 ，袁新哲，庞于涛，沈国煜

(同济大学 土木工程防灾国家重点实验室，上海 200092)

非线性参数拟合的桥梁概率地震需求模型研究

袁万城 ，袁新哲，庞于涛，沈国煜

(同济大学 土木工程防灾国家重点实验室，上海 200092)

针对云图法建立概率地震需求模型时部分工程需求参数(EDP)与地震动强度参数(IM)间不满足对数线性回归关系假设的问题，建立某三跨混凝土连续梁桥的3D有限元模型。采用IDA方法建立桥梁概率地震需求模型，并以IDA分析结果为基准，在同一地震动参数下，采用基于不同拟合方式的云图法建立概率地震需求模型并得到了结构在不同破坏状态下的易损性曲线。研究表明，当EDP与IM之间的数量关系不满足云图法对数线性关系基本假设时，选择恰当的非线性参数拟合方式可以显著提高云图法建立概率地震需求模型的精度。

概率地震需求模型；云图法；IDA分析；非线性拟合；易损性分析；连续桥梁

美国太平洋地震工程研究中心(PEER)在2005年提出新一代基于性能的地震工程研究框架。其中，概率性的地震需求分析作为该框架的重要一环，其核心在于建立概率地震需求模型。概率地震需求模型通常被假设为对数正态分布模型[1]，可以用2种方法来建立：云图法和IDA分析方法。云图法假设工程需求参数EDP的均值与地震动参数IM之间满足对数线性关系，而模型对数标准差在整个IM范围内保持不变[2]。IDA分析方法通过将地震波调幅至不同强度，统计EDP在不同IM时的分布特性来建立概率地震需求模型。近年来，国内外学者对云图法和IDA方法进行了广泛的研究与运用：Kevin Mackie等[3]利用云图法对结构进行非线性动力时程分析，来获得结构的概率地震需求模型；冯清海[4]运用IDA分析方法对特大桥梁的地震易损性与地震风险概率进行了分析；Payam Tehrani[5]等运用快速IDA算法对不同地震类型作用下的连续四跨直梁桥地震反应进行了分析研究。一般来说，在使用云图法建立概率地震需求模型时，为了保证其分析精度，需要对所选取的IM参数的有效性进行评估，确保其与EDP均值服从云图法对数线性关系的假设。Luco Nicolas等[6]研究了速度脉冲型地震IM参数与剪切型多自由度体系顶层非线性变形需求的相关性，分析了不同IM参数的有效性。但这种IM参数有效性评估的方法只适用于特定的地震类型和结构类型，由于地震动的强烈不确定性和结构类型的多样性，IM参数的有效性也是不确定的。因此，通过改变EDP与IM参数之间的回归拟合方式解决EDP与IM参数之间的非线性对数关系问题，可以提高云图法建立概率地震需求模型的精度。

1 概率地震需求模型与易损性分析

1.1 概率地震需求模型

桥梁结构地震风险分析中最主要的步骤是建立桥梁结构的地震易损性曲线，而桥梁结构的地震易损性曲线建立的关键步骤是进行概率地震需求分析，得到概率地震需求模型。分别可以采用云图法和IDA分析方法来得到桥梁结构的概率地震需求模型。

对于云图法而言，重点在于运用能量法则进行统计回归分析得到桥梁结构构件的地震峰值响应与地震动强度参数的关系。其基本步骤[7]为：选取可以反映结构所在场地区域地质情况的地震动纪录；建立结构三维有限元模型；进行非线性时程分析，得到IM与EDP的样本；通过能量法则，对样本进行回归分析得到结构构件的概率地震需求模型。根据能量法则，IM与EDP的均值μD一般服从对数线性关系：

(1)

式中：a、b为回归参数，两边取对数后方便运用最小二乘法进行拟合，其拟合方差可由下式计算：

(2)

式中：n为非线性时程次数，EDPi为结构的地震峰值响应。得到模型均值和方差后，即可得到相应的概率地震需求模型：

(3)

IDA分析方法与云图法的主要区别在于IDA通过统计结构需求在不同地震动强度下的分布特性，获得模型均值和方差，然后即可由式(3)建立结构的概率地震需求模型。云图法基于对数线性关系假设建立的概率地震需求模型具有高度相似性，而IDA分析方法统计在不同地震动强度下结构响应分布特性，可以视为一种更加精确的概率地震需求模型建立方法。因此，以IDA分析结果为基准，可以比较不同拟合方式下的云图法建立概率地震需求模型的精度，研究非线性拟合方式下的概率地震需求模型。

1.2 地震易损性分析

概率地震需求模型中，结构的地震需求与地震动输入强度息息相关，而结构的能力通常用来定义不同的损伤状态函数[8]。对于一个特定的损伤状态，结构构件的失效概率Pf可由桥梁结构的地震需求Sd与结构的能力Sc表示：

(4)

由于地震需求Sd与结构的能力Sc均假设为对数正态分布，因而失效概率Pf可用标准正态分布函数表示为

(5)

式中：βc与βd分别为能力与需求的对数正态分布的方差。由于IDA分析方法并不需要假定特定级别的地震动强度下的地震响应的概率分布函数的类型，因而IDA方法在计算结构损伤概率的时候相对简单，可由下式计算：

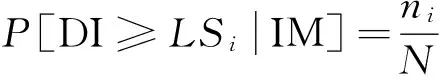
(6)

式中:ni为超过极限状态函数的IDA曲线的数目，N为IDA曲线的总数，DI为损伤指标，LSi为给定损伤指标的极限状态值。基于IDA易损性分析结果，得到采用不同拟合方式的云图法下桥梁结构响应的概率地震需求模型，并建立桥梁构件的易损性曲线，研究不同拟合方式对易损性分析精度的影响。

2 计算模型及地震波选取

2.1 模型简介

以一座三跨混凝土连续梁桥为例，墩截面采用正方形柱，截面为1.5m×1.5m，墩高为8m，跨径布置为3m×38m。图1给出了混凝土桥梁的总体布置图。主梁采用C50预应力混凝土，桥墩混凝土为C40，钢筋采用HRB335，纵向配筋率为0.8%，配箍率0.5%。使用OpenSees建立桥梁3D非线性有限元模型，上部结构在地震作用下基本保持弹性，使用线弹性梁柱单元模拟，墩柱采用弹塑性纤维单元模拟，用碰撞单元考虑地震作用下主梁与桥台的碰撞效应。为简化起见，本例中不考虑桩土共同作用，假定墩底固结。分别选取桥梁墩台位移aD固定支座位移aZ和桥墩截面曲率aQ为需求参数，建立其在同一地震动参数下的概率地震需求模型。

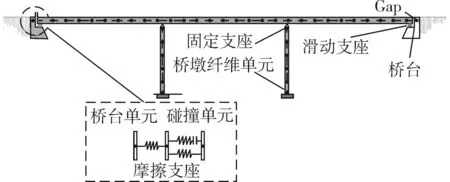
图1 混凝土连续梁桥总体布置图Fig. 1 Overall layout of RC continuous beam bridge

2.2 地震波选取

从PEER强震记录数据库中选取了40条地震波，这些波的震级为6.0～6.7，并且各条地震波的震中距均大于10 km，地震持时均取为30 s。图2给出了40条波阻尼为5%的伪加速度反应谱曲线以及反应谱概率分布。考虑云图法模型精度受样本点数目影响，对选取的40条地震波进行调幅处理，得到80条地震波输入来增加样本点数目，避免因样本点数目较少而带来的分析误差。在进行IDA分析时，对选取的40条地震波进行0.1g-1.0 g的调幅处理，来统计结构响应在不同地震动强度下的分布特性。

(a) 1#

(b) 2#图2 地震波反应谱及概率分布图Fig. 2 Response spectrum and probability distribution of 40 seismic waves

地震动可以通过PGA、PGV、SA(T)等强度指标来描述。Padgett等[9]通过对地震动参数进行效率、可适用性以及危害的可计算性评价表明：PGA是比较适合的地震动强度指标。因此，本文选用PGA作为地震动强度参数。由于选取的研究模型为三跨混凝土连续梁桥，桥型较简单，地震波输入时只考虑了沿纵桥向的单方向输入。

3 计算分析

3.1 云图法与IDA分析结果

分别采用基于对数线性假设的云图法和IDA方法得到桥梁墩台位移aD，固定支座位移aZ和桥墩截面曲率aQ响应均值与PGA的对数回归曲线，如图3所示。从图中对比结果可以发现，墩台位移aD和PGA间具有显著的对数线性关系，满足云图法的基本假设。但支座位移aZ和桥墩截面曲率aQ与PGA之间具有显著的非线性对数关系，其概率地震需求模型不再适用基于线性对数关系假设的云图法来建立。通常EDP均值与IM间的对数线性关系假设不满足时，应该选择其他IM参数。然而如果找到一种能够拟合EDP均值与IM参数之间非线性对数关系的方式，则同样可以提高云图法概率地震需求模型的精度。

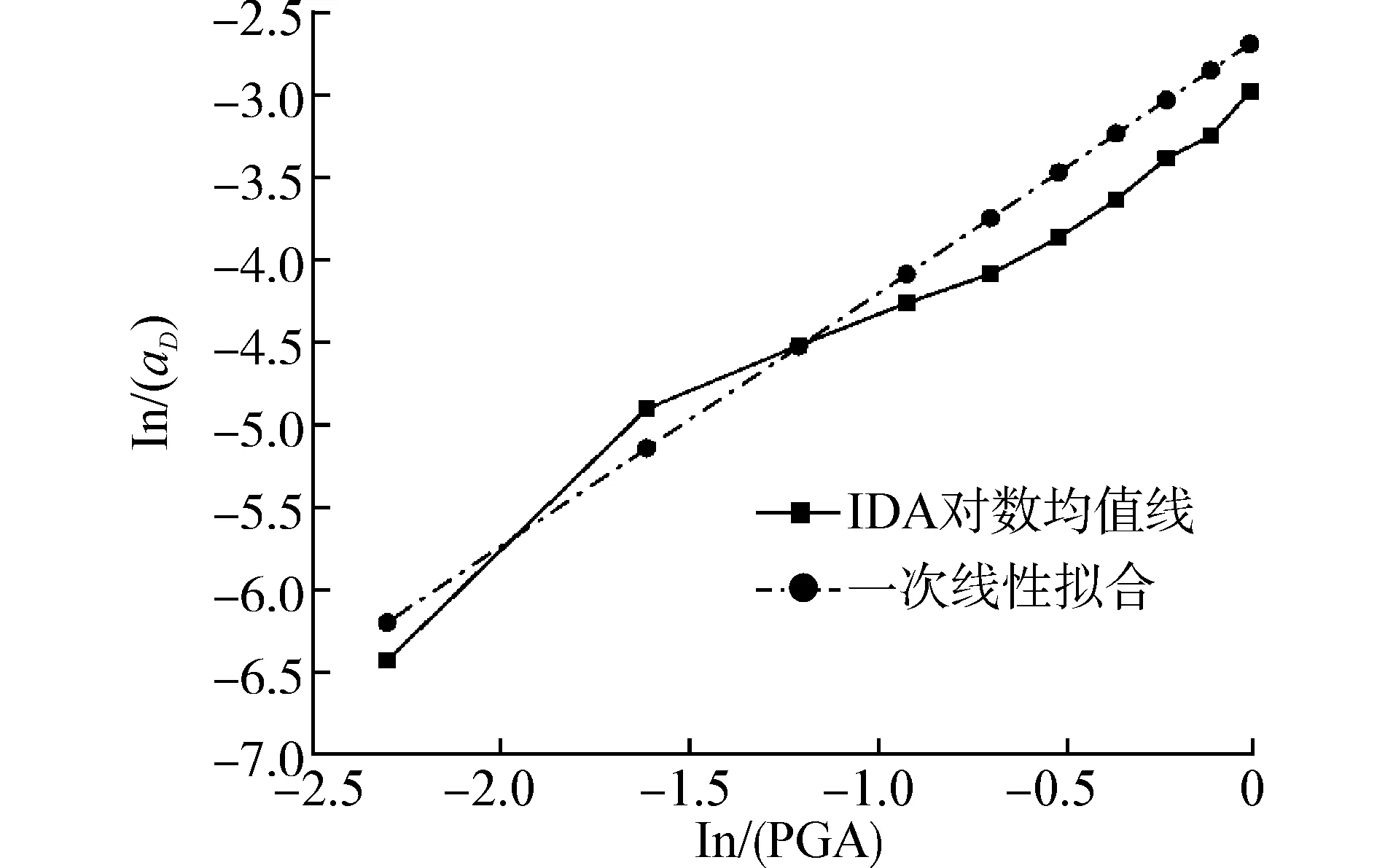
(a) 墩台位移aD

(b) 墩台位移aZ

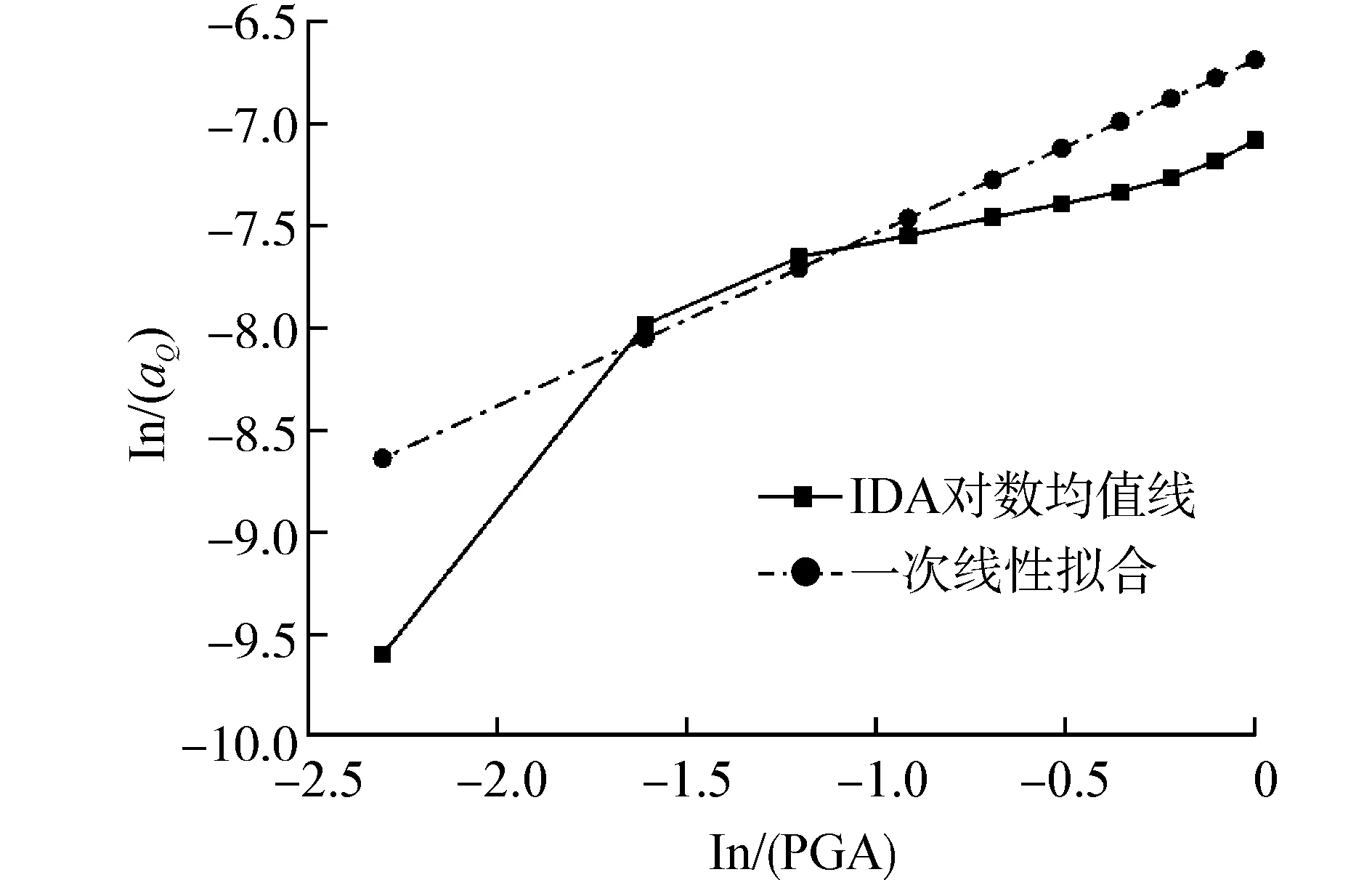
(c) 墩台截面曲率aQ图3 云图法与IDA分析结果比较Fig. 3 Comparison between cloud method and IDA method

为了拟合结构响应aZ，aQ与IM间的非线性对数关系，基于最小二乘原理采用一次线性、二次抛物线和三次抛物线拟合EDP均值与PGA参数间的对数回归关系，得到的桥梁墩台位移aD, 固定支座位移aZ和桥墩截面曲率aQ与PGA的对数曲线关系如图4所示。由图可见，虽然墩台位移aD与PGA间具有显著的线性对数回归关系，但依然给出其不同拟合方式下的对数回归关系曲线，来对比说明回归拟合方式的改变对概率地震需求模型精度的影响。改变拟合方式后墩台位移aD基于非线性拟合的回归分析精度并未有提高，非线性拟合曲线与IDA曲线偏离。而支座位移aZ，桥墩截面曲率aQ采用非线性拟合方式可以得到与PGA间的非线性对数关系。从图4(b),(c)可以看出，三次抛物线回归拟合方式得到的IM对数关系曲线与IDA结果最为吻合。这表明当所选地震动参数不能满足云图法对数线性关系假设时，采用三次抛物线可以建立EDP均值与PGA参数间的非线性对数关系，根据不同地震动强度下桥梁结构响应，即可得到基于非线性拟合方式的云图法概率地震需求模型。

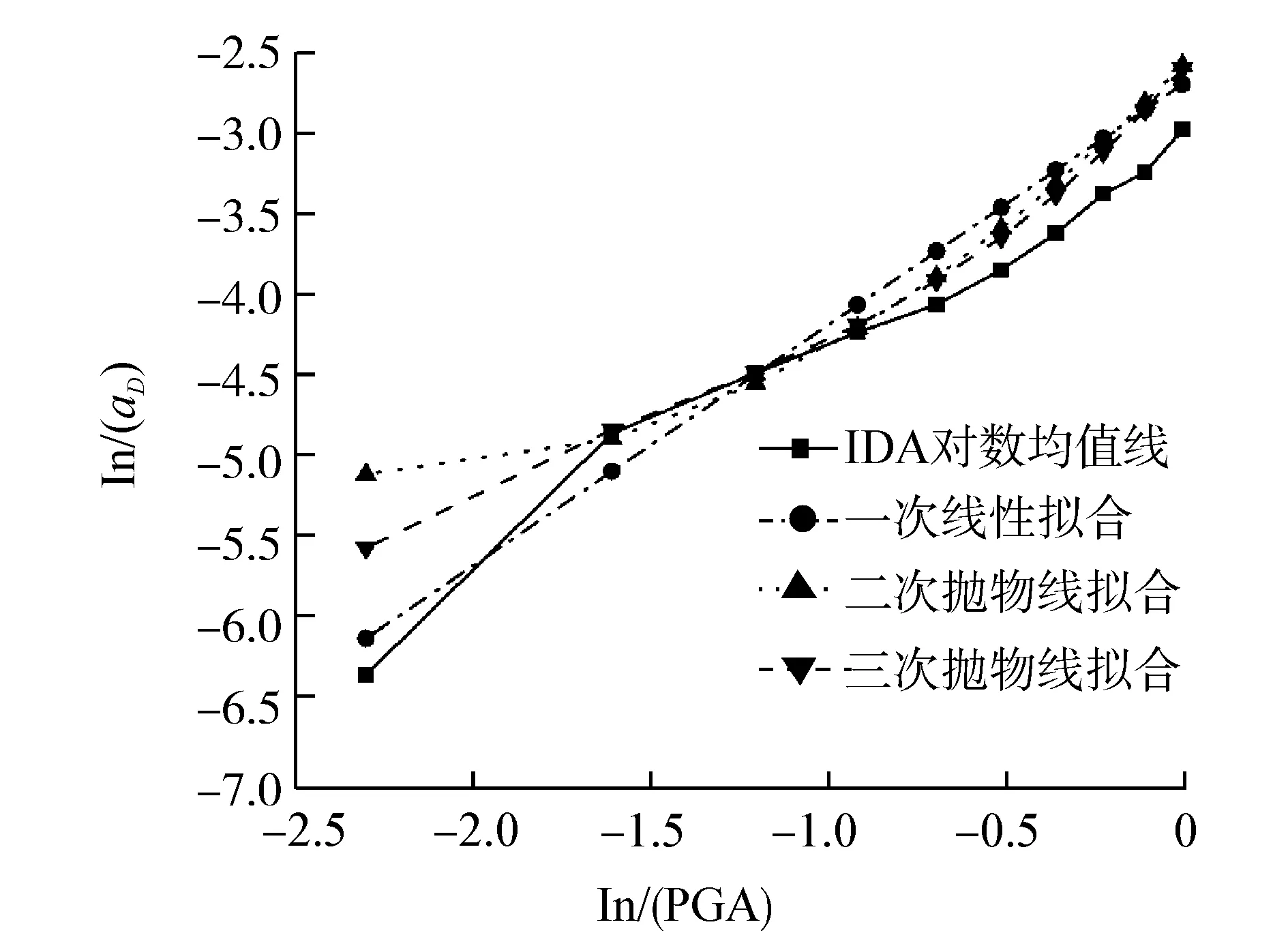
(a) 墩台位移aD

(b) 支座位移aZ

(c) 墩台截面曲率aQ图4 不同拟合方法的云图法与IDA分析结果比较Fig. 4 Comparison between cloud methods under different fitting methods and IDA

因此，当云图法对数线性关系假设不成立时，可以采用非线性拟合在不改变地震动参数IM的条件下建立EDP均值与IM的关系曲线，可以提高云图法概率地震需求模型的精度。同时需指出，采用最小二乘法的高次抛物线回归拟合并非唯一的非线性回归拟合方式，也可采用其他非线性回归拟合手段来建立更加精确的EDP与IM参数之间的数量关系。

3.2 不同拟合方式的易损性分析

采用非线性拟合方式建立结构概率地震需求模型后，即可对构件易损性进行分析。为比较不同拟合方式对易损性分析精度的影响，得到了不同拟合方式下桥墩的易损性曲线。选择桥墩而不是相对来说更加容易破坏的支座进行易损性分析是因为桥墩截面曲率aQ与PGA的非线性更加明显。进行易损性分析时，选用变形作为破坏准则[10]，结构性能划分标准分为：1)轻微破坏；2)中等破坏；3)严重破坏；4)倒塌。

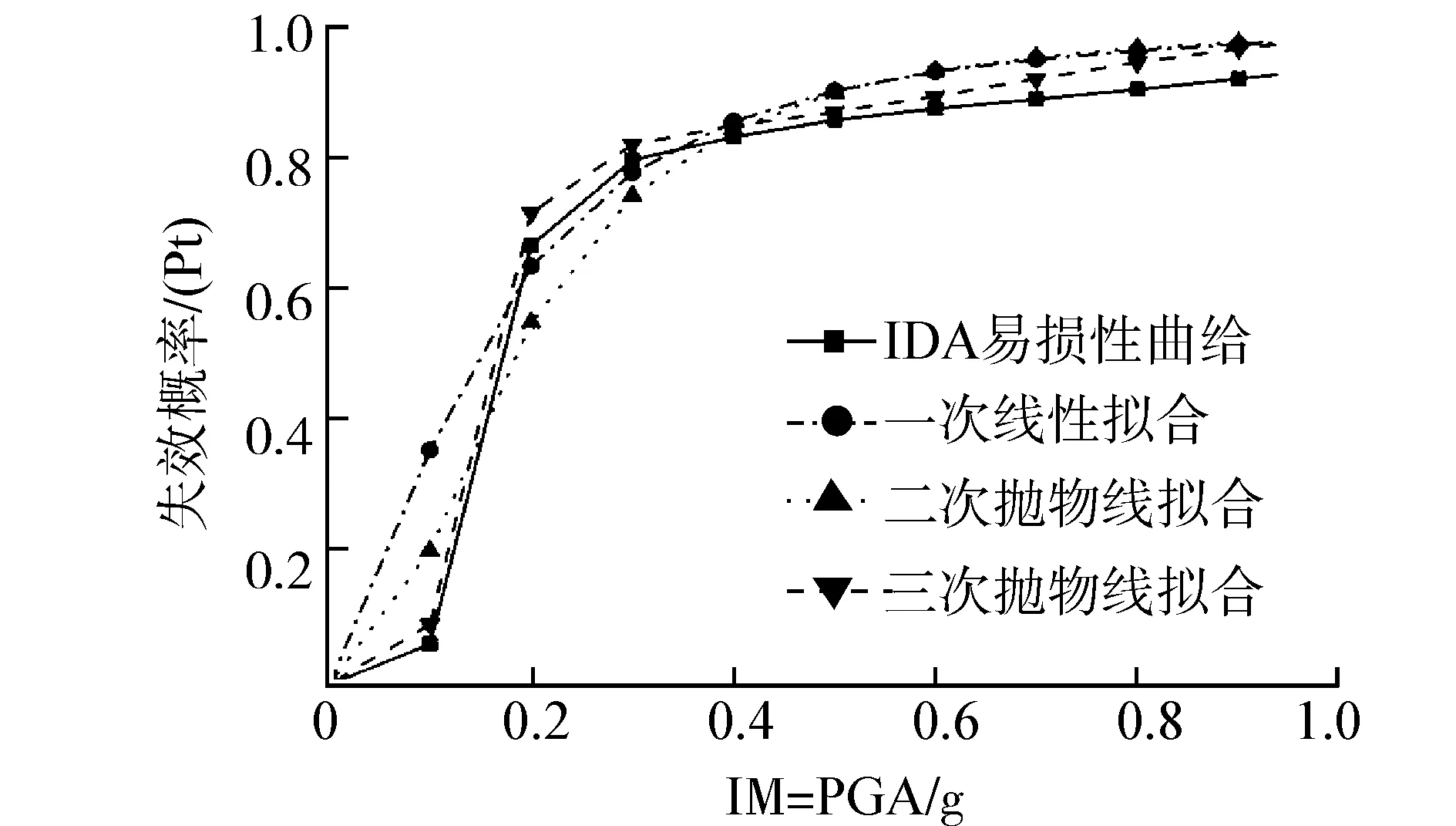
(a)轻微损伤

(b) 中等损伤

(c) 严重损伤

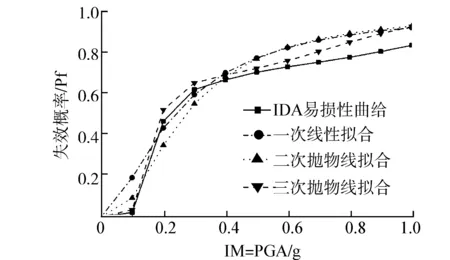
(d) 完全破坏图5 不同拟合方式下桥墩在不同损伤状态的易损性曲线Fig. 5 Fragility curves under different damage states by different fitting ways

图5分别对应给出了4种破坏状下基于IDA方法和不同拟合方式云图法得到的易损性曲线。从图5可以看出，采用三次抛物线拟合得到的易损性曲线与IDA分析结果最为逼近。因此，采用非线性拟合方法建立EDP与IM参数之间的关系，可以对结构易损性进行更加精确的计算，提高桥梁结构可靠度评估的准确性。

4 结束语

本文以某三跨RC连续梁桥为例，选择PGA为地震动指标，桥梁墩台位移aD，固定支座位移aZ和桥墩截面曲率aQ为工程需求参数，以IDA分析结果为基准，采用非线性拟合方式的云图法建立了桥梁结构的概率地震需求模型，并得到了桥墩构件的易损性曲线，得出以下结论：对结构进行概率地震需求分析时，如果所选EDP与IM参数之间不满足云图法对数线性回归关系的基本假设，可以通过非线性拟合方式建立EDP与IM参数之间的数量关系，建立结构的概率地震需求模型。基于非线性拟合的概率地震需求分析与易损性分析结果与IDA分析结果吻合良好，计算精度较高。

[1]张菊辉, 胡世德. 桥梁地震易损性分析的研究现状[J]. 结构工程师, 2005, 21(5): 76-80. ZHANG Juhui, HU Shide. State of the art of bridge seismic vulnerability analysis research[J]. Structural Engineers, 2005, 21(5): 76-80.

[2]于晓辉, 吕大刚, 王光远. 关于概率地震需求模型的讨论[J]. 工程力学, 2013, 30(8): 172-179. YU Xiaohui, LYU Dagang, WANG Guangyuan. Discussions on probabilistic seismic demand models[J]. Engineering Mechanics, 2013, 30(8): 172-179.

[3]MACKIE K, STOJADONOVIC B. Probabilistic seismic demand model for California highway bridges[J]. Journal of Bridge Engineering, 2001, 6(6): 468-481.

[4]冯清海. 特大桥梁地震易损性与风险概率分析[D]. 上海: 同济大学, 2008. FENG Qinghai. Study on seismic vulnerability and risk probability analysis of super-Large bridge[D]. Shanghai: Tongji University, 2008.

[5]TEHTANI P, MITCHELL D. Seismic response of bridges subjected to different earthquake types using IDA[J]. Journal of Earthquake Engineering, 2013, 17(3): 423-448.

[6]LUCO N, CORNELL C A. Structure-specific scalar intensity measures for near-source and ordinary earthquake ground motions[J]. Earthquake Spectra, 2007, 23(2): 357-392.

[7]PANG Yutao, WU Xun, SHEN Guoyu, et al. Seismic fragility analysis of cable-stayed bridges considering different sources of uncertainties[J]. Journal of Bridge Engineering, 2014, 19(4): 111-122.

[8]钟剑, 庞于涛, 沈国煜, 等. 采用拉索减震支座的斜拉桥地震易损性分析[J]. 同济大学学报: 自然科学版, 2014, 42(3): 351-357. ZHONG Jian, PANG Yutao, SHEN Guoyu, et al. Seismic fragility analysis of cable-stayed bridges retrofitted with cable-sliding friction aseismic bearing[J]. Journal of Tongji University:Natural Science, 2014, 42(3): 351-357.

[9]PADGETT J E, NIELSON B G, DESROCHES R. Selection of optimal intensity measures in probabilistic seismic demand models of highway bridge portfolios[J]. Earthquake Engineering & Structure Dynamics, 2008, 37(5): 711-725.

[10]沈国煜, 袁万城, 庞于涛. 基于Nataf变换的桥梁结构地震易损性分析[J]. 工程力学, 2014, 31(6): 93-100. SHEN Guoyu, YUAN Wancheng, PANG Yutao. Bridge seismic fragility analysis based on NATAF transformation[J]. Engineering Mechanics, 2014, 31(6): 93-100.

[11]庞于涛, 袁万城, 沈国煜, 等. 基于结构易损性分析的公路桥梁可靠度研究[J]. 哈尔滨工程大学学报, 2012, 33(9): 1092-1096. PANG Yutao, YUAN Wancheng, SHEN Guoyu, et al. Reliability analysis of highway bridges based on structural vulnerability analysis[J]. Journal of Harbin Engineering University, 2012, 33(9): 1092-1096.

A probabilistic seismic demand model by nonlinear parameter fitting method

YUAN Wancheng, YUAN Xinzhe, PANG Yutao, SHEN Guoyu

(State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China)

In order to solve the problem that when establishing a probabilistic seismic demand model by the cloud method, some Engineering Demand Parameters (EDPs) and ground motion intensity (IM) parameters do not meet the assumption of logarithmic linear regression relationship, a 3D finite element model of a three-span concrete continuous beam bridge was established. The bridge probabilistic seismic demand model was first established by incremental dynamic analysis(IDA). Taking the IDA analysis result as the benchmark, under the same seismic motion parameters, and using the cloud method based on various fitting modes to establish a probabilistic seismic demand model, the fragility curve under different breaking states was obtained. The results show that, when the quantitative relationship between EDP and IM does not meet the basic logarithmic linear relationship assumption of the cloud method, choosing appropriate nonlinear parameter fitting mode can significantly improve the precision of the probabilistic seismic demand model established by the cloud method.

probabilistic seismic demand model; cloud method; IDA; nonlinear fitting; fragility analysis;continuous beam bridge

2014-08-29.

时间：2015-08-24.

土木工程防灾国家重点实验室基金资助项目(SLDRCE14-B-14)；国家自然科学基金资助项目(51478339,51278376).

袁万城(1964-), 男, 研究员,博士生导师； 袁新哲(1989-), 男, 硕士研究生.

袁新哲, E-mail:yxz_hz@163.com.

10.3969/jheu.201408046

U442.5

A

1006-7043(2015)09-1212-05

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.U.20150824.1603.001.html