阻尼对三自由度弹性碰撞系统周期运动倍化分岔的影响研究

王 强 汪少铭 刘永葆 贾小权 赵雄飞 董 瑞

（海军工程大学动力工程学院1） 武汉 430030） （海军东海舰队舰艇训练中心2） 上海 201900）（海军驻哈尔滨703所军事代表室3） 哈尔滨 150078） （海军旅顺装备技术质量监测站91315部队4） 旅顺 116041）

0 引 言

在机械设备中，由于故障间隙导致的系统碰撞振动时有发生，系统阻尼对系统的其非线性动力学行为也有密切关系。赵文礼等［1］对碰撞阻尼器振动系统推导了周期解存在的条件，并利用Poincare映射和数字仿真研究了该系统的倍周期分岔、HOPF分岔及拟周期环面破裂等分岔进入混沌运动的非线性行为。戎海武等［2］用Zhuravlev变换将碰撞系统转化为速度连续的非碰撞系统，然后用随机平均法得到了关于慢变量的随机微分方程，讨论了系统阻尼项、非线性项、随机扰动项和碰撞恢复系数等参数对于系统响应的影响。刘莉等［3］以一类含非黏滞阻尼的Duffing单边碰撞系统为研究对象，运用复合胞坐标系方法，分析了该系统的全局分岔特性，发现，随着阻尼系数、松弛参数及恢复系数的变化，系统发生混沌吸引子与其吸引域内的混沌鞍发生碰撞而产生的内部激变和混沌吸引子与吸引域边界上的周期鞍（混沌鞍）发生碰撞而产生的常规边界激变。徐慧东等［4］研究了一类两自由度分段线性弹性系统Nermark－Sacker分岔、倍化分岔、亚谐分岔现象。徐斌等［5］针对平面上的分段线性连续系统，研究了同宿轨的存在性及同宿分岔问题。朱喜锋等［6］研究了两自由度含间隙弹性碰撞系统模型，分析了该系统在低频下单周期多碰撞周期运动及颤振运动特性及转迁规律。国外，Shaw等［7］对一类在简谐激振力作用下有单侧约束的单自由度振子做了研究，用中心流形定理分析了周期运动的局部分岔，并通过同宿相截条件讨论了混沌运动。Peterka［8］研究了具有粘滞阻尼的碰撞振子中的擦边分岔、周期倍化分岔和鞍结分岔之间的转迁现象。K.Czotlczyński［9］研究了气动轴承的线性、非线性刚度和阻尼系数确定方法，找到其阻尼系数与轴承参数与外部负载，角速度和振动频率的关系。Leine等［10］对非光滑系统周期解的不连续分岔作了进一步的研究，分析了伴随基解矩阵的跳跃而发生的各种不连续分岔现象。Luo等［11］研究了一个分段线性周期激励系统，通过建立相应映射，研究各类稳定和不稳定的周期运动。虽然国内外学者在非光滑领域进行了大量的研究，取得了丰硕的成果，但其选择一般是低维自由度数，且是固定的碰撞面，而在大多数设备运行中质块发生故障碰撞都是相对移动的。因此本文基于非线性理论，建立三自由度移动碰撞面非光滑模型，首次从理论结合数值仿真研究了该情况下系统由倍化分岔通向混沌的非线性行为，同时分析了阻尼对系统分岔、混沌等非线性行为的影响，为设备设计及故障诊断提供依据并为大型设备的运转和故障分析提供技术支持。

1 三自由度弹性碰撞系统的运动及分析过程

首先，建立三自由度分段弹性模型，见图1.M1，M2，M3分别为3个物体的质量；X1，X2，X3分别为M1，M2，M3的运动的位移；C1，C2，C3分别为M1与M2的阻尼，M2与M3之间阻尼，M3与固定端阻尼；K1，K2，K3分别为3个物体之间的刚度，K4为碰撞时质块突变的接触刚度；F1sin（Ω1T），F2sin（Ω2T）分别为作用在 M1，M2的等效作用力；D为碰撞间隙；Ω1与Ω2分别为质块M1，M2，的旋转频率.

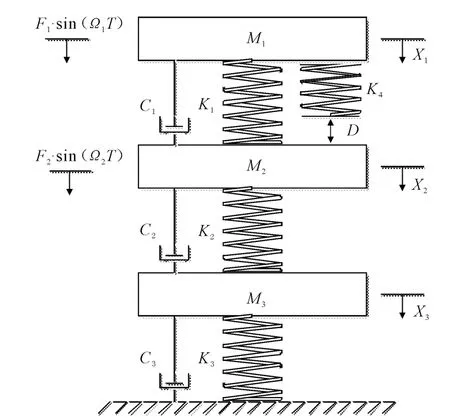
图1 三自由度移动碰撞面弹性系统模型

图2 系统二维相平面图

为了描述该系统的运动过程，引入一个分界面.首先定义边界函数，E＝X1－X2－D，分界面可表示为

该分界面用来区分物块M1与M2刚接触或分离的状态，分别表示碰撞前的系统运动区间V－，碰撞后的运动区间V＋，这样状态空间被分界面分成2部分，见图2.图中：V＋＝ ｛X ∈（X1，X2）＞0｝表示物块与断弹簧K4接触状态；V－＝ ｛X ∈（X1，X2）＜0｝ 表示物块与断弹簧K4分离状态.

根据上面的分析，可建立系统的运动学方程：

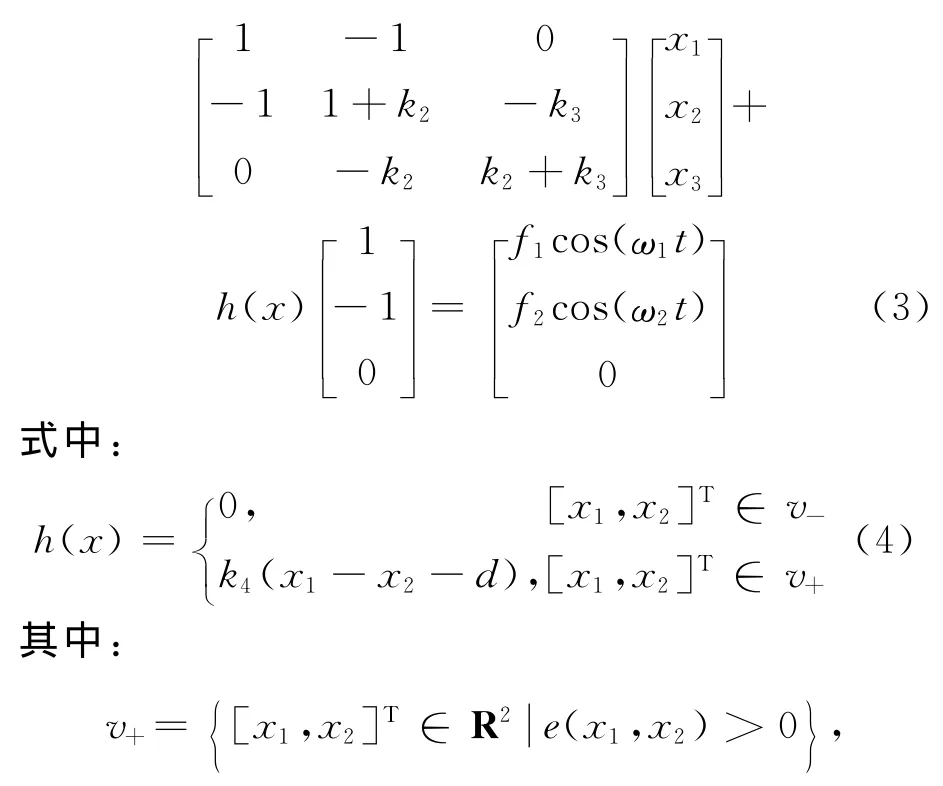
2 系统周期运动倍化分岔的Floquet特征乘子分析

将系统（3）和（4）写为如下的规范式：

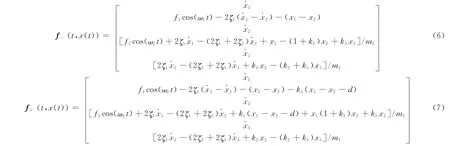
设系统（5）的一个解x（t）从区域v－出发，即x（t0）∈v－.在t＝tp时刻到达分界面∑.系统在区间B＝｛t∈≤t≤tp｝是连续的，相应的基解矩阵也是连续的.然而由于向量场f（t，x（t））在分界面处的非光滑性使得相应的Jacobian矩阵在分界面处通常是不连续的，这将引起系统整个基解矩阵不连续，因此在不连续处需要求出相应的切换矩阵.

下面求分界面处的切换矩阵.

1）从区域v－进入区域v＋时，对超平面∑：e＝x1－x2－d＝0，有法向量n＝ ［1，0，1，0，0，0］T，设一周期解x（t）到达分界面∑的时间为t1并交于点xt1.在t1时刻计算切换矩阵如下.

2）从区域v＋进入区域v－，设周期解x（t）到达分界面∑的时间为t2并交于点，在时刻t2有切换矩阵

下面求各光滑区域的基解矩阵.在区域v－系统的运动方程为

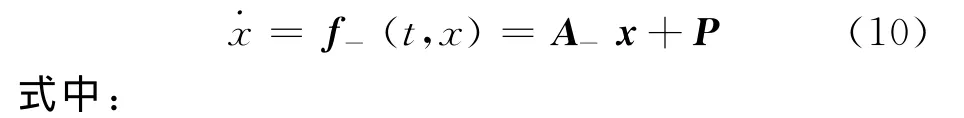
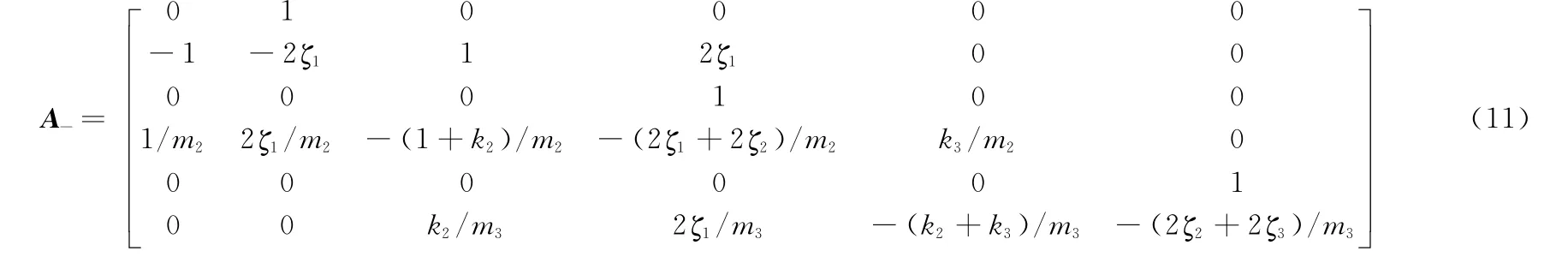
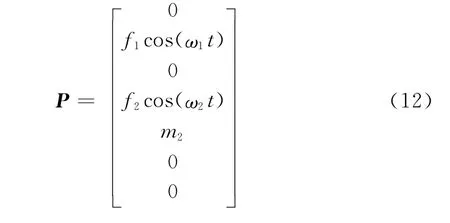
方程（10）的扰动在周期解x（t）处线性化系统的基解矩阵为

将切换矩阵（8）和（9）结合各子空间相应的基解矩阵（13）和（14）经过合成可得全局的单值矩阵.

于是系统的Floquet特征乘子即为单值矩阵（15）的特征值.对于系统（5）这样的非光滑系统，由于分界面是光滑的，系统的Floquet特征乘子是连续穿越单位圆周的.当有一个Floquet特征乘子沿实轴从（－1，0）穿出单位圆，其他特征乘子仍位于单位圆内时，系统（5）稳定的周期解将发生倍化分岔.

3 数值分析

为了通过数值仿真进一步揭示滚动轴承系统（3）和（4）的倍化分岔通向混沌的现象，在分界面∑处取Poincare截面如下.

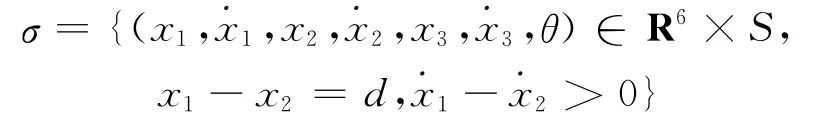
式中：θ＝ω1t；b＝R（mod 2π）为1个实数对2π取余数.

选取系统（3）和（4）的一组无量纲化参数：d＝0.001；f1＝20；f2＝0；m2＝0.02；m3＝30；ζ1＝0.05；ζ2＝0.08；ζ3＝0.02；k2＝50；k3＝80；k4＝10.以旋转频率ω1为分岔参数.

当ω1＝2.283 353 17；时（ωs为系统临界分岔的旋转频率），系统对应的其中一个Floquet特征乘子为λ1＝λ（ωs）＝－0.999 998，接近单位圆周上的（－1，0）点；其他的特征值

仍在单位圆周内.由此可见系统在ω1＝2.289 667 851 2时发生了倍化分岔.系统随ω1变化的分岔图见图3.

图3 系统的分岔图

图4 ω1＝2.25时单周期运动的相图和庞加莱截面图

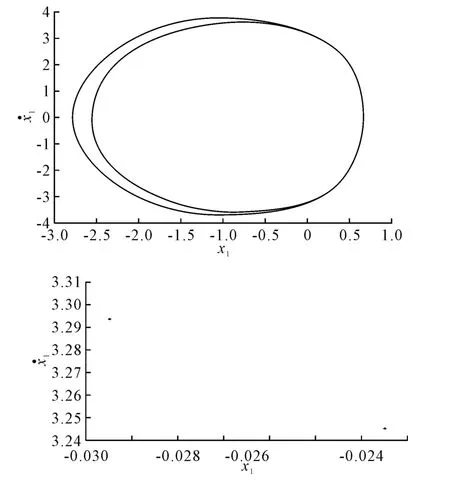
图5 ω1＝2.284时周期二运动的相图和庞加莱截面图

由图3可见，系统起初处于稳定的单周期运动（见图4）.当ω1＝2.283 353 17；时，系统经历倍化分岔并过渡到周期二运动 （见图5～6）.随着旋转频率ω1的增加，在ω1＝2.35时，系统处于周期四运动（见图7），在ω1＝2.42时系统处于周期八运动（见图8），当旋转频率进一步增加时，系统最终通向了混沌运动（见图9），如庞相莱截面上的奇怪吸引子.

图6 ω1＝2.3时周期二运动的相图和庞加莱截面图

图7 ω1＝2.35时周期四运动的相图和庞加莱截面图

图8 ω1＝2.42时周期八运动的相图和庞加莱截面图

同时研究了不同的阻尼系数对系统分岔的影响（见图10），从图10可以明显看出，阻尼系数增加对系统的振动有很大的衰减作用，随着阻尼系数的增大，系统的混沌状态和分岔形式都变的简单，尤其是图10c），在旋转频率ω1相同的范围内，系统只出现了一个简单的倍化分岔.

图9 ω1＝2.44时运动的相图和庞加莱截面图

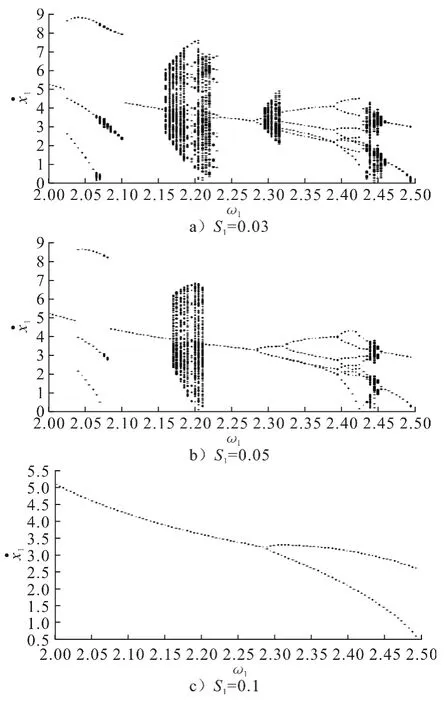
图10 不同的阻尼系数对系统分岔的影响

4 结束语

文中建立了三自由移动碰撞面非光滑系统模型，应用Floquet理论分析了该系统周期运动发生倍化分岔的条件.结果表明系统有1个Floquet特征乘子接近－1，其余Floquet特征乘子的模都小于1，系统在该点发生了倍化分岔，数值仿真进一步研究了系统由倍周期分岔通向混沌的非线性现象.同时研究不同的阻尼系数对系统分岔的影响，发现增大阻尼可以有效的减少系统的分岔混沌等非线性行为，该项研究可以为实际设计提供理论指导.

［1］赵文礼，周晓军.碰撞阻尼器系统的分岔、混沌与控制［J］.振动工程学报，2007，20（2）：161－167.

［2］刘 莉，徐 伟，岳晓乐，等.一类含非黏滞阻尼的Duffing单边碰撞系统的激变研究［J］.物理学报，2013，62（20）：1－8.

［3］戎海武，王向东，徐 伟，等.窄带随机噪声作用下单自由度非线性碰撞系统的响应［J］.应用力学学报，2010，27（1）：73－82.

［4］徐慧东，谢建华.一类两自由度分段线性非光滑系统的分岔与混沌［J］.振动工程学报，2008，21（3）：279－286.

［5］徐 斌，唐 云，杨凤红，等.分段线性连续系统中的同宿分岔［J］.动力学与控制学报，2013，11（1）：31－35.

［6］朱喜锋，曹兴潇.两自由度弹性碰撞系统的颤振运动及转迁规律［J］.兰州交通大学学报，2014，33（4）：191－195.

［7］SHAW S W，HOLMES P J.A periodically forced piecewise linear oscillator［J］.Journal of Sound and Vibration，1983，90（1）：129－155.

［8］PETERKA E.Bifurcation and transition phenomena in an impact oscillator［J］.Chaos，Solitons and Fractals，1996，7（10）：1635－1647.

［9］CZOTLCZY？SKI K.How to obtain stiffness and damping coefficients of gas bearings［J］.Wear，1996，201：265－275.

［10］LEINE R I，NIJMEIJER H.Dynamics and Bifurcation of Non－Smooth Mechanical Systems［M］.Berlin：Springer，2004.

［11］LUO A C J，CHEN L.Periodic motions and grazing in a harmonically forced，piecewise，linear oscillator with impacts［J］.Chaos，Solitons and Fractals，2005，24：567－578.