近场爆炸作用下水面目标毁伤研究

张永坤 刘文思

（91439部队 大连 116041）

0 引 言

目前国内外学者通常根据所研究问题的特点，对水下爆炸载荷的2个阶段冲击波和爆炸气泡作用阶段分别进行研究［1－4］，对相应的毁伤情况进行了广泛的研究［5－8］.当结构距离爆源较近时，造成船体结构局部破坏的主要载荷为冲击波载荷.

文中选取目标是为考核鱼雷近场爆炸下对典型舰艇的局部毁伤效应，其主要破坏载荷为冲击波.仿真计算使用的硬件平台为高性能集群系统，最高可对1 000万网格的水下爆炸仿真模型进行仿真计算，其采用的平行计算技术和搭载的128核计算软件能实现对水下爆炸作用机理的更精确模拟和快速计算.仿真计算使用的软件为ABAQUS软件，其采用的是声固耦合法，此方法是采用声学单元模拟流场，载荷包含了冲击波和气泡脉动的综合作用，同时还考虑了空化压力的影响.

1 仿真计算过程

以曙光5000集群系统为计算平台，以128核并行版ABAQUS大型有限元计算软件为仿真计算手段，以某水面舰舱段为目标舰，针对320kg TNT当量爆破型战斗部的远场冲击威力和近场毁伤能力进行仿真计算.

1.1 仿真方法验证

结合某实船爆炸数据，对仿真方法进行验证.计算工况为1 000kg TNT距左舷70m，水深50 m沉底爆，龙骨冲击因子为0.337.根据当时爆炸时测点的实际情况选取进行比对的测点位置，分别选择了3个应变测点和3个加速度测点.测点具体位置分别在：01甲板55＃肋位迎爆面中纵桁纵向应变测点、主甲板25＃肋位迎爆面纵桁纵向应变测点、内底45＃肋位迎爆面第一扶强材边中间根部板格应变测点、01甲板27＃肋位舰长室垂向加速度测点、主甲板76＃肋位垂向加速度测点、内底47＃肋位垂向加速度测点.对比结果见表1～2.

表1 应变峰值对比

表2 加速度峰值对比

通过对峰值的相对误差计算，得出应变峰值平均精度77.48%，加速度峰值平均精度77.52%，平均相对误差均在30%以内，计算精度符合工程要求.

1.2 仿真计算对象

计算对象以某舰为原型，截取舰中两个舱段为计算模型，长度约为20m，型宽17m，型深12 m.有限元模型见图1.

图1 有限元模型

1.3 仿真工况设计

仿真试验共设置了7个工况，工况设计主要依据水中兵器的装药量及使用情况，其中第一个工况采用验证算法工况相同的冲击因子.模型计算工况设置见表3.

表3 模型计算工况设置

1.4 测点选取

模型共设置了11个测点，测点位置均位于模型中横剖面位置，见表4和图2.

表4 水面目标靶模型测点位置

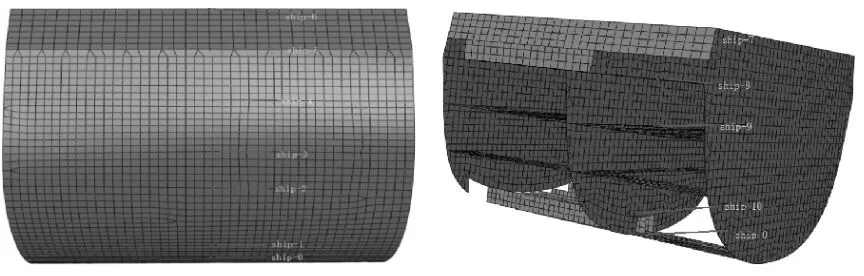
图2 水面目标靶模型测点位置

1.5 仿真计算结果

1.5.1 测点加速度计算结果

gk－7爆源位于模型长度方向中部距左舷7.5 m，水深7.7m舷侧爆炸，针对320kg TNT当量的战斗部毁伤能力进行仿真计算（冲击因子为2.32）.仿真结果显示：模型舷侧及前后横舱壁的均出现了较大塑性变形及破口，结构基本损坏.应力云图、不同位置加速度变化及峰值变化曲线见图3～6.

图3 初始时刻应力云图

图4 最终状态应力云图

图5 模型中部甲板处加速度变化曲线

图6 模型中甲板处加速度峰值变化曲线

通过一系列的水面毁伤目标等效靶仿真试验研究表明：舱段前后隔板部分是最先出现变形和破口的部分，且在爆炸距离较远处也会因爆炸冲击造成结构震荡损坏甚至破口，这主要是因为水面舱段模型是从原始舰艇直接摘取的，前后隔板没有进行加固改造，是舱段结构最为脆弱的部分；沉底水雷对舱段主要是以冲击损伤为主，冲击波对薄弱部位直接造成结构塑性变形甚至轻微破口，更严重是对结构造成震荡损伤，会引起整个主甲板的大面积变形以及前后隔板的震荡破损；鱼雷对模型的损伤在远距离时也是以冲击震荡为主，会引起局部震荡破口，在距离较近时以冲击波冲击毁伤为主，同时也会产生局部震荡破口.在结构加速度峰值变化方面，外板垂向加速度度峰值会随着结构位置的升高而迅速变小，但在01甲板附近出现再次增大趋势；在爆源距离较远时各层甲板中部垂向加速度峰值会随着甲板升高而迅速下降，但在爆源距离较近时，在2甲板附近垂向加速度峰值最大，上下均迅速变小的类似正态分布趋势.

由于水面毁伤目标等效靶设计结构的前后隔板原始模型结构较脆弱，不能代表整船结构局部强度，需要进行加固处理，其他结构部位可基本保持不变.因此，水面毁伤目标等效靶结构经仿真试验验证设计基本合理，只要前后隔板处经加固后，就可达到设计要求.

2 毁伤理论方法及等级评定

2.1 局部毁伤形式

毁伤最简单形式就是塑性变形，塑性变形是一个动态过程.当塑性变形达到一定程度，板的厚度由于变得太薄，板被撕裂，形成破口.所以，破口是一种比塑性毁伤来得严重的毁伤形式.通常定义为严重毁伤.一般的破口不会造成船体的沉没.但是当破口的范围很大时，船体迅速进水，就有可能造成船体的沉没.因此，船体沉没是最严重的毁伤形式.水中爆炸造成的毁伤分为4级，见表5.

表5 毁伤的4个级别

2.2 局部毁伤量化

局部结构塑性毁伤为

式（1）表明结构毁伤是在2个因素的联合作用下产生的：第一个因子是能量密度SF，它表达了冲击环境；另一个因子是（σsh）1／2，表达了结构的抗损能力.式（1）可作为代替冲击因子评估毁伤的一个公式.考虑到无量纲化，可以将式（1）变换为下式：

RF为抵抗因子，它代表结构对冲击的抵抗能力.该值越大，它的抗爆能力就越大；反之，它的抗爆能力就越小.定义

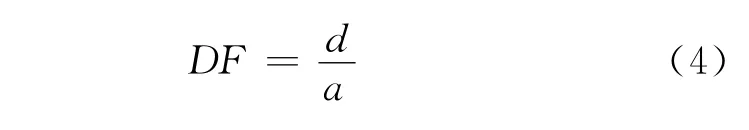
DF为毁伤因子，它代表结构的毁伤情况.

毁伤因子事实上是应变的平方根（圆板应变的平方根和毁伤因子相等），亦即

式（5）说明了毁伤因子的物理意义.

将式（3）和式（4）代回式（2），得到

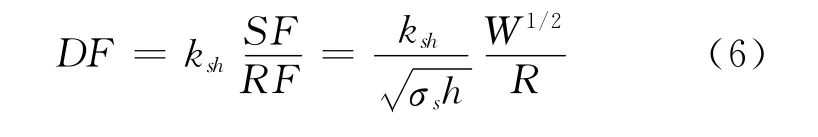
式（6）具有非常明显的直观含义，毁伤因子与冲击因子成正比与抵抗因子成反比.

任意炸药水下爆炸作用下的毁伤因子为

式中：W 为药包的质量，kg；R为药包距目标的距离，m；σs为材料的屈服极限，Pa；a为板格相当长度；h为板的相当厚度，m；ksh≈300为常数；Cm和Cγ为与炸药相关的常数，其数值可以通过实验的方法确定.

2.3 水面舰艇的毁伤等级划分

毁伤因子和毁伤等级的关系曲线，见表6.

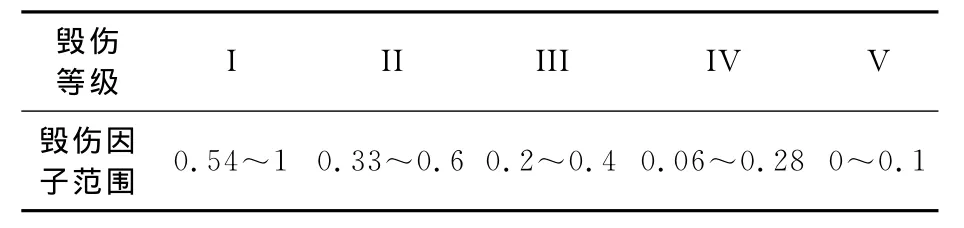
表6 水面舰艇的毁伤等级划分

3 仿真方法与理论分析方法比对

根据选择的战斗部类型以及计算目标，采用式（6）计算毁伤因子，根据表6对照说明毁伤的情况.首先根据仿真工况计算出目标的冲击因子，其次根据目标特征计算其抵抗因子，再次根据冲击因子及抵抗因子计算出根据毁伤等级确定毁伤因子的值，结果见表7.

参照表5（毁伤级别）及表6（水面舰艇毁伤等级划分），由表7可知，工况1，2，3的毁伤因子对应的等级为4级（轻微毁伤，出现轻微塑性变形）、4级、4级至3级（中等毁伤，出现严重塑性变形），与仿真计算所描述的毁伤情形相比较，两者比较吻合.工况4，5，6，7的毁伤因子对应的毁伤等级为5级至4级、4级、3级至2级、2级（严重毁伤，出现破口），与仿真计算结果基本一致.

表7 水面目标毁伤因子

4 结 论

1）结合实船数据对仿真计算方法进行验证，证明了仿真计算方法的可信性，为目标毁伤仿真计算奠定基础.

2）采用仿真计算方法对水下爆炸作用下的目标的毁伤情况进行计算，同时采用毁伤理论对其毁伤情况进行分析.

3）对两种方法的计算结果进行比对，2种方法的计算结果比较吻合.

［1］于政文.冲击载荷作用下简支方板的理论解［J］.振动与冲击，1999，18（1）：17－22.

［2］RUDRAPATNA N S，VAZIRI R，OLSON M D.Deformation and failure of blast－loaded square plates［J］.Int J Impact Engng，2000，24：457－474.

［3］贾宪振，胡毅亭，董明荣，等.水下爆炸冲击波作用下平板塑性动力响应的数值模拟［J］.舰船科学技术，2007，29（6）：41－44.

［4］ZONG Z.A hydroplastic analysis of a free－freebeam floating on water subjected to an underwaterbubble［J］.Journal of Fluids and Structures，2005，20：359－372.

［5］谌 勇，唐 平，汪 玉，等.刚塑性圆板受水下爆炸载荷时的动力响应［J］.爆炸与冲击，2005，25（1）：90－96.

［6］李世铭.船舶水下接近爆炸多层结构毁伤特性研究［D］.哈尔滨：哈尔滨工程大学，2012.

［7］李海涛，张永坤.近场水下爆炸作用下箱型梁整体损伤特性研究［J］.兵工学报，2012，33（5）：611－616.

［8］张 弩，宗 智.水下爆炸气泡载荷对舰船的总体毁伤研究［J］.中国造船，2012，53（3）：28－39.