基于全波形反演的探地雷达数据逆时偏移成像

雷林林, 刘四新, 傅磊*, 吴俊军

1 吉林大学地球探测科学与技术学院, 长春 130026 2 中国石油集团东方地球物理勘探有限责任公司 新兴物探开发处， 河北涿州 072751



基于全波形反演的探地雷达数据逆时偏移成像

雷林林1, 刘四新1, 傅磊1*, 吴俊军2

1 吉林大学地球探测科学与技术学院, 长春 130026 2 中国石油集团东方地球物理勘探有限责任公司 新兴物探开发处， 河北涿州 072751

逆时偏移成像(RTM)常用来处理复杂速度模型，包括陡倾角及横向速度变化剧烈的模型.与常规偏移成像方法(如Kirchhoff偏移)相比，逆时偏移成像能提供更好的偏移成像结果，近些年逆时偏移成像越来越广泛地应用到勘探地震中，它逐渐成为石油地震勘探中的一种行业标准.电磁波和弹性波在动力学和运动学上存在相似性，故本文开发了基于麦克斯韦方程组的电磁波逆时偏移成像算法，并将其应用到探地雷达数据处理中.时间域有限差分(FDTD)用于模拟电磁波正向和逆向传播过程，互相关成像条件用于获得最终偏移结果.逆时偏移成像算法中，偏移成像结果受初始模型影响较大，而其中决定电磁波传播速度的介电常数的影响尤为重要.本文基于时间域全波形反演(FWI)算法反演获得了更为精确的地下介电常数模型，并将其反演结果作为逆时偏移成像的初始介电常数模型.为了验证此算法的有效性，首先构建了一个复杂地质结构模型，合成了共偏移距及共炮点探地雷达数据，分别应用常规Kirchhoff偏移算法及逆时偏移成像算法进行偏移处理，成像结果显示由逆时偏移成像算法得到的偏移结果与实际模型具有较高的一致性；此外本文在室内沙槽中进行了相关的物理模拟实验，采集了共偏移距及共炮点探地雷达数据，分别应用Kirchhoff和叠前逆时偏移成像算法进行处理，结果表明叠前逆时偏移成像在实际应用中能获得更好的成像效果.

逆时偏移； 探地雷达； 全波形反演； 物理模拟实验

1 引言

偏移是一种地震成像技术，它在空间域或时间域将记录到的同向轴归位到真实的反射界面.传统的地震偏移成像方法基于单程波方程，并将多次散射波当做噪声处理，但对于复杂地质结构及大倾度界面如裂缝，合理的利用多次散射信息至关重要.传统波动方程偏移方法如Kirchhoff积分偏移(Gray, 1986; Gray and May, 1994; Docherty)难以适应横向速度变化；有限差分波动方程偏移(Vidale, 1988; Mufti et al., 1996)近似求解波动方程，存在倾角限制；频率波数域偏移方法(Loewenthal and Mufti, 1983)是基于常速度模型，当地下介质速度存在变化时会出现明显的精度问题.有别于传统的基于单程波方程的偏移方法，逆时偏移(Baysal et al., 1983; Levin, 1984; Chang and McMechan, 1986，1994; Sun and McMechanz, 2001; Yoon et al., 2003; 刘欣欣等, 2013; 王保利等, 2012)基于全波方程，能够精确的处理沿任意方向传播的波场，包括耦合波及横纵波之间的转换波，从而可更精准地将波场归位到其真实的地下空间位置.虽然逆时偏移技术的成功应用实例并不多见，但它在勘探地震中受到越来越多的关注，逆时偏移包括叠前逆时偏移和叠后逆时偏移.

探地雷达电磁波与地震波在运动学和动力学存在一定的相似性，此外，采集到的探地雷达数据和地震数据都是空间位置的时域电压信号，故而在一定程度上勘探地震中的数据处理技术可以运用到探地雷达数据处理中.Fisher(1992)提出用基于张量波动方程的逆时偏移算法对单通道的共偏移距的探地雷达数据进行了偏移处理，处理后的结果在一定程度显示了该算法的优越性.Feng和Sato(2004)利用叠前逆时偏移算法，对地雷探测中采集到的多偏移距数据进行处理，一方面强散射波得到压制，另一方面获得了地下更为精细的雷达剖面图像.Zhou等(2005)应用一种基于遗传算法的偏移速度分析方法，对合成及野外实测的共炮点雷达数据进行分析获得了地下介电常数分布，并以其作为叠前逆时偏移的初始速度模型，取得了较好的结果.

本文开发了电磁波逆时偏移算法，电磁波场的正向及逆向传播是基于时间域有限差分方法，单轴各向异性完全匹配层(UPML)(Fang and Ying, 2009; Feng and Dai, 2011)吸收边界条件用于吸收边界的反射波，互相关成像条件用于获得空间图像.应用电磁波全波形反演算法，对合成及实测的共偏移距、多偏移距探地雷达数据全波形反演，获得了与实际情况更为接近的地下介质分布情况.通过全波形反演获得的介电常数和电导率模型作为逆时偏移的初始模型，逆时偏移的结果与基于共偏移距雷达数据Kirchhoff偏移成像结果对比发现，逆时偏移成像效果明显好于传统偏移成像结果.

2 逆时偏移基本原理及电磁波逆时偏移算法

传统的偏移算法基本是基于单程波方程深度外推，所以在对多分量地震资料处理过程中首先要进行纵、横波分离，然后用现有的偏移算法分别处理纵波场和横波场.它的缺陷在于：1)将多分量地震资料当作几个标量波的简单叠加，忽略了地震波的矢量特性，从而影响地震多分量资料的处理与解释精度；2)假如地震波场横波与纵波没有完全分离(目前这种现象广泛存在)，而在实际资料的偏移处理过程中又假设为标量波场，这必然会使偏移结果产生许多人为假象，影响处理精度.逆时偏移与传统的偏移方法有很大的不同，逆时偏移可以看成是波场在时间轴上逆向传播过程，当波场倒退到零时刻，则所有反射波与绕射波的能量都回到最初被反射和绕射的空间位置，应用成像条件即可得到最终的偏移成像剖面.逆时偏移的波动理论方法基于全波方程，波场可以沿各个方向传播，因此该方法不受介质倾角限制，适用于速度任意变化的模型.

逆时偏移算法的实现概括起来主要包括三个步骤：第一是震源波场正向延拓；第二是接收波场的逆时延拓；第三是应用成像条件成像.前两个步骤的实现可以基于相同的数值方法，本文应用时间域有限差分法(刘四新和曾昭发, 2007; 刘四新等, 2006; Taflove and Hagness, 2005; Liu and Sato, 2005; Liu et al., 2007; Liu et al., 2011)实现电磁波场在空间的正向和逆向传播.影响叠前逆时偏移成像效果的一个非常重要因素是成像条件(Chattopadhyay and McMechan, 2008)的应用，Claerbout(1971)提出的互相关成像条件是最基础的成像条件，它采用零延迟互相关成像条件，该成像条件的不足之处在于对首波及背景散射波做互相关会产生低频噪声，其次应用该成像条件得到的成像结果与地下介质的反射系数没有对应关系.鉴于零延迟互相关成像条件的弊端，后续逐步发展了反褶积成像条件(Guitton et al., 2007)、震源补偿成像条件(Guitton et al., 2006)、扩展成像条件(Sava and Fomel, 2006)以及角度域成像条件(Yoon and Marfurt, 2006)等.标准的逆时偏移采用零延迟互相关成像条件，其计算公式为：

(1)

其中IMAG(x)为地下空间x的成像结果，S(x,t,si)为源波场，R(x,T-t,si)为接收波场，t和si分别代表时间和源序号.当接收波场传播到时间t时，读取震源波场t时刻的场值和对应时刻接收波场的场值并将两波场值相乘，最后将计算区域对应网格点相加即可得到最终成像结果.

本文开发的电磁波逆时偏移成像算法如图1所示，对于合成数据，首先给定真实模型，通过FDTD模拟电磁波在模型中的传播过程，同时记录接收波场.逆时偏移成像的第一步是通过FDTD进行激励源波场的正向传播模拟，使用雷克子波作为激励源函数，电磁波最大传播时间序列为nmax，为了节约存储空间，将每个时刻模型空间的外围波场存储；第二步是电磁波波场的逆向传播模拟，该步骤包括两个方面的反向传播过程：(一)利用包围模型空间外围全时序波场恢复电磁波场的正向传播过程，这样做的目的其实就是以时间换空间；(二)利用接收波场进行电磁波场的逆向传播模拟；第三步是成像条件的应用，因为互相关条件容易实现且无稳定性问题，本文选取互相关作为成像条件.波场逆向传播的过程中，利用成像条件获得每个时刻的偏移图像，当波场传播到时间零点，将各个时刻的图像叠加即可获得单源逆时偏移成像结果.此外，通过去噪技术去除低频影响，再将所有单源偏移结果叠加得到最终的逆时偏移成像结果.

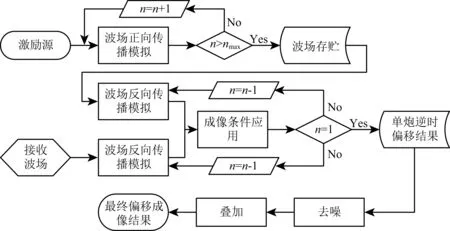
图1 电磁波逆时偏移成像算法流程Fig.1 RTM algorithm flow for electromagnetic wave

3 数值模拟实验

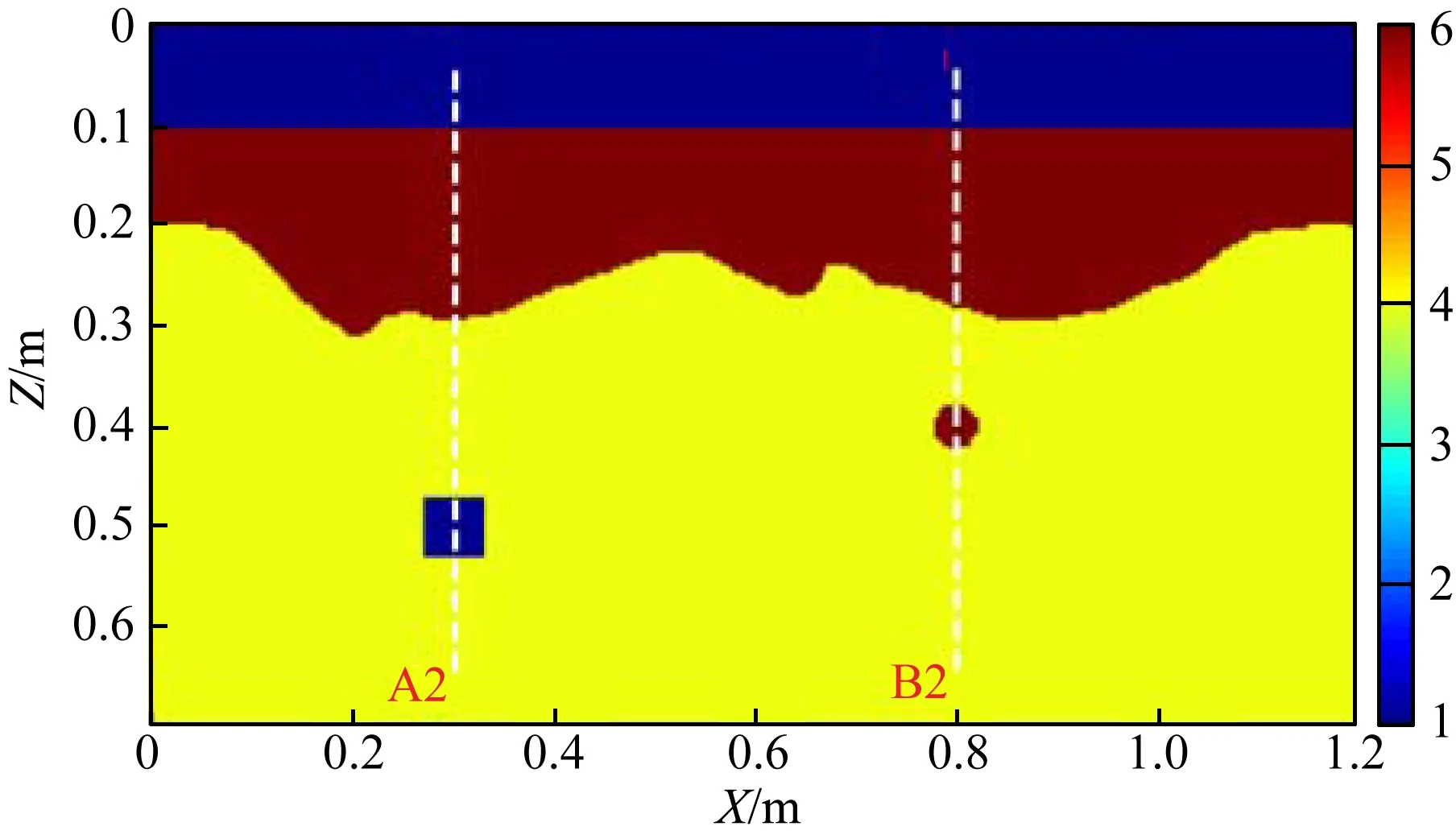
图2 相对介电常数模型Fig.2 Relative dielectric constant model

文中构建了一个复杂地质结构模型如图2所示，X方向长度为1.2 m，Z方向长度为0.7 m.图中蓝色区域代表空气，暗红色区域代表土壤层，其相对节电常数为6，电导率为5 mS·m-1，平均厚度约为0.12 m，该土壤层的底界面起伏变化；黄色区域代表干沙层，其相对介电常数为4，电导率为1 mS·m-1，平均厚度约为0.48 m.由于土壤层与干沙层之间存在大倾角起伏界面，故而该模型中存在变化剧烈的横向速度.干沙中埋有2个异常体，其中蓝色方形区域代表一个高速异常体，其相对介电常数为1；圆心位于(0.8, 0.4)m处圆形暗红色区域代表一个低速异常体，其相对介电常数为6，电导率为4 mS·m-1.

3.1 雷达合成数据

典型的雷达反射测量中，电场与测线往往是垂直的，因此我们应用二维TM模FDTD求解Maxwell方程组，同时采用UPML吸收边界条件来减少边界处反射.为确保稳定性及减少数值频散，设置网格大小为0.004 m，发射源为主频1600 MHz的雷克子波，时间取样间隔0.008 ns，采样点为1024.首先合成了共偏移距剖面探地雷达数据，第一道信号发射天线的水平距离位于0.05 m，接收天线与发射天线间距为0.05 m，发射天线的移动步长为0.012 m，沿地面总该采集了88道雷达信号，水平方向上覆盖了1.05 m的水平距离.图3a是合成的共偏移距雷达剖面，横坐标代表道号，纵坐标代表雷达波的双程走时，从图可知在2.5～4.5 ns之间的双曲线同向轴是来自土壤层和沙层界面的反射波，值得注意的是出现了来自不规则界面拐点处的若干散射波，这些散射杂波会对地下目标的识别造成困扰.水平位置位于第20道，顶点约在6 ns出现的双曲线同向轴来自方形高速异常体的反射波，而水平位置位于第60道，顶点约为4.8 ns处出现的双曲线同向轴则是来自圆形低速异常体的反射波.合成的共炮点雷达数据如图3b所示，水平轴代表道号，纵轴是雷达波的双程走时.共炮点雷达数据集与共偏移距雷达剖面在某种程度上存在一定的相似性，来自界面及异常的反射波出现的双程走时相当，此外反射波的曲线形态也存在一定的相似性.

3.2 基于全波形反演的初始模型建立

逆时偏移成像算法中，影响最终成像效果的一个最重要因素是初始模型.为了获得一个较高精确度的初始模型，本文采用时间域全波形反演技术，反演地下介质的相对介电常数分布，从而为逆时偏移成像提供更为精准的初始模型.全波形反演技术试图利用包括走时、幅度、相位等全波形信息来反演地下参数分布，它比常规的基于射线的成像方法能提供更加可靠的参数信息，本文应用的时间域全波形反演技术细节可参考(Meles et al., 2010, 2011)，其主要目的是建立包含观测数据和模拟数据的目标函数(2)式：

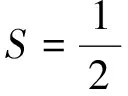
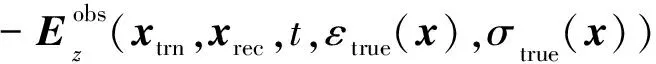
(2)

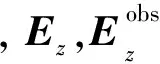
时间域全波形反演算法中，不管是单参数分别反演还是介电常数和电导率联合反演，初始介电常数和电导率模型的选取至关重要.考虑到如图2所示的真实相电常数模型中存在起伏较大的界面，地下介电常数模型不易给定，故而这里选取的初始介电常数模型如图4a所示，蓝色区域代表空气；黄色区域代表地下介质，其相对介电常数为4.5.图4b是时间域全波形反演25次迭代反演后得到的相对介电常数结果，首先土壤与沙层之间的起伏界面得到了清晰的刻画，起伏界面的形状及位置与真实模型匹配较好，另外在反演的界面上方相对介电常数要高于界面下方的相对介电常数；反演图像中埋于沙层中的两个异常体得到了较好的刻画，两个异常体的水平位置与实际模型相对应.右侧低速异常体的位置与真实模型一致，而且其内部相对介电常数值高于周围背景值；左侧高速异常体的位置与真实模型一致，其内部相对介电常数值低于背景值.

图5给出了真实模型、初始模型及反演结果之间的详细数值比较，黑色实线代表真实模型的相对介电常数值，蓝色虚线代表初始模型相对介电常数值，红色实线是时间域全波形反演迭代25次后的反演结果.图5a是经过左侧圆形异常体A1-A2线(见图2)的相对介电常数比较，横轴为相对介电常数值，纵轴对应的空间位置.小于0.1m时，反应在真实模型中是相对介电常数为1空气，可以发现三条曲线完全重合.0.1～0.3m之间，给出的初始模型与真实模型之间存在1.5的差异，而全波形反演结果基本介于初始模型与真实模型之间.在0.3m处是界面突变点，反演结果中在同样位置出现了拐点.0.5m附近是异常体所在的位置，反演结果的数值大小及拐点位置与真实模型基本一致.图5b是经过右侧圆形异常体B1-B2线(见图2)的相对介电常数比较，从中可以得到与左图相似的结论：全波反演的结果较为准确的刻画了地下相对介电常数分布情况，可以为逆时偏移提供更为精准的初始模型.

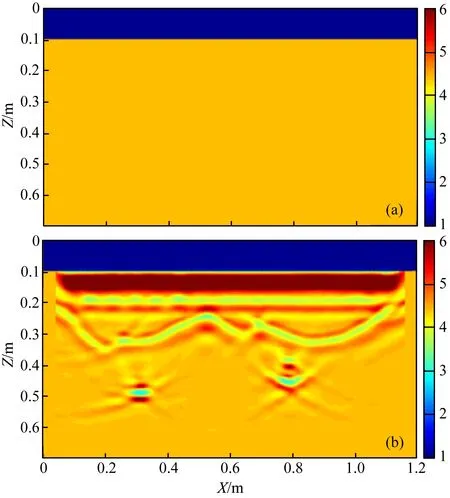
图4 (a)初始介电常数模型； (b)全波形反演25次迭代后的介电常数反演结果Fig.4 (a) The initial permittivity model for the FWI inversion； (b) the inversion permittivity results after 25 iterations

图5 真实模型，初始模型及时间域全波反演结果在不同位置的介电常数比较(a) A1-A2线(见图2)介电常数比较; (b) B1-B2线(见图2)介电常数比较.Fig.5 The permittivity comparison of true model, initial model and FWI inversion results at different position(a) Permittivity comparison of A1-A2 line (the left black dash line indicated in Fig.2); (b) Permittivity comparison of B1-B2 line (the right black dash line indicated).

3.3 合成数据逆时偏移成像分析

为了评价逆时偏移算法应用到探地雷达数据处理中的效果，选取Kirchhoff偏移算法与之比较.对于逆时偏移成像算法，我们可以将其处理共偏移距数据，亦可以处理共炮点数据.

对于如图3a所示的共偏移距雷达数据，基于真速度模型，用Kirchhoff偏移成像算法获得的偏移成像结果图6a所示.从图可知，来自不规则界面的反射波得到一定程度的抑制，可以大致识别出土壤与沙层的界面，然而土壤与沙层界面的散射波没有完全收敛，仍然存在较严重的杂波干扰.偏移剖面中，来自两个异常体的反射波能量基本上得到了压制.左侧高速异常体水平位置与真实模型一致，但是垂直位置与实际模型存在一定的偏差；右侧低速异常体的位置与实际模型基本一致.此外需要注意的是成像结果中出现了一些干扰杂波，这些杂波的存在将使得雷达数据的解释工作更加复杂.因此，对于存在横向速度变化较大的模型，即便使用真实速度模型进行Kirchhoff偏移，也得不到良好的偏移结果.

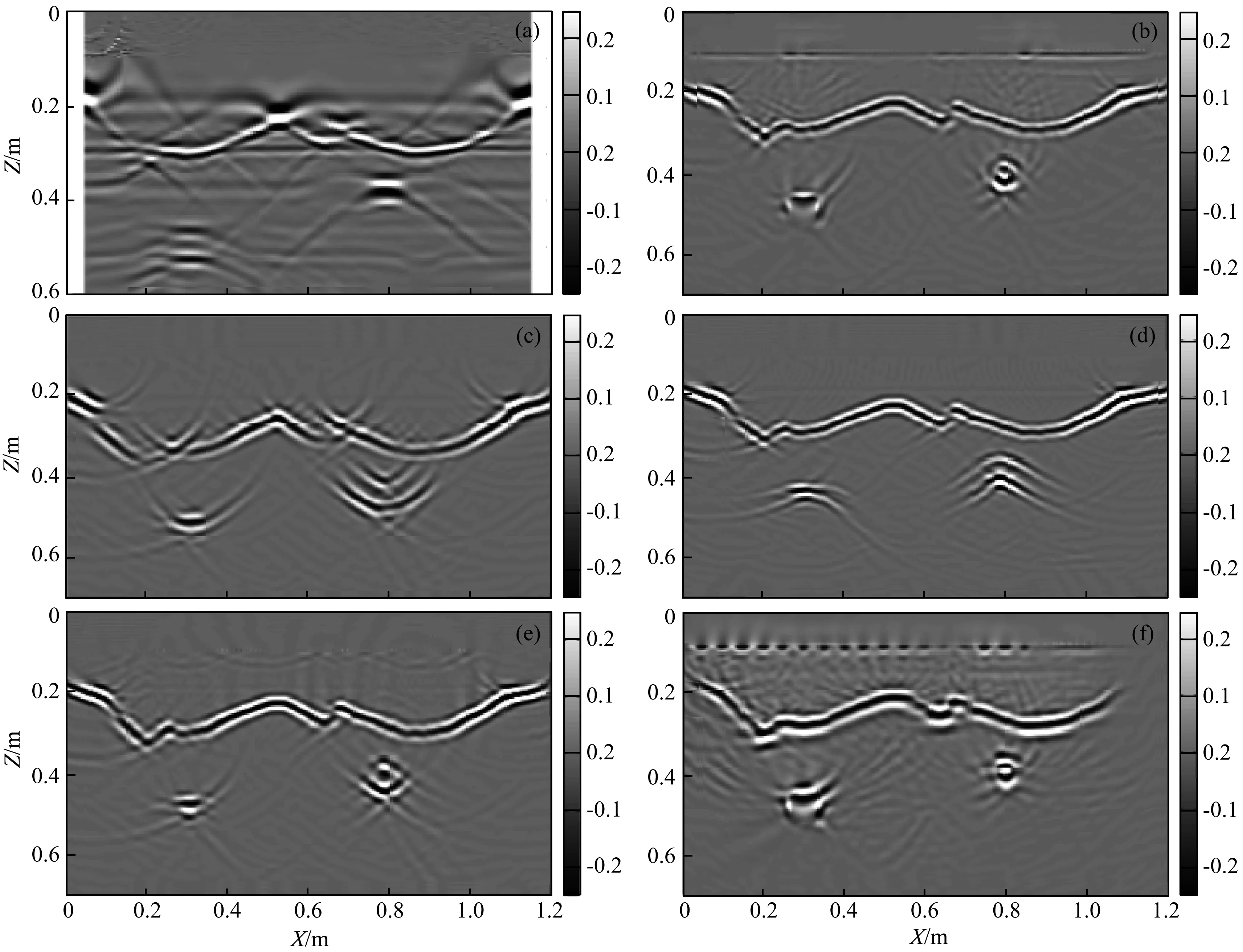
图6 不同偏移方法应用不同初始模型得到的成像结果(a) 基于共偏移距数据的Kirchhoff偏移结果(真介电常数模型作为初始模型); (b)基于共偏移距数据的RTM结果(真介电常数模型作为初始模型); (c) 基于共偏移距数据的RTM结果(地下相对介电常数取4作为初始模型); (d) 基于共偏移距数据的RTM结果(地下相对介电常数取6作为初始模型); (e) 基于共偏移距数据的RTM结果(FWI反演结果作为初始模型); (f) 基于共炮点雷达数据集的RTM结果(真介电常数模型作为初始模型). 所有图像都进行了振幅归一化.Fig.6 Imaging results from different migration methods with different initial model(a) The Kirchhoff migration result based on common offset radar data (true dielectric constant model as the initial model); (b) RTM result based on common offset radar data (true dielectric constant model as the initial model); (c) RTM result based on common offset radar data (dielectric constant of 4 in the underground as the initial model); (d) RTM result based on common offset radar data (dielectric constant of 6 in the underground as the initial model); (e) RTM result based on common offset radar data (FWI result as the initial model); (f) RTM result based on common shot radar data (true dielectric constant model as the initial model). All figures are normalized by their maximum amplitude.

同样，对于如图3a所示的共偏移距雷达数据，将真介电常数模型作为初始模型参数，忽略电导率的影响，用逆时偏移成像获得的成像结果如图6b所示，可以发现来自起伏界面的散射波已被完全压制住了，土壤与沙层间的界面可以被清晰的识别出来，成像后的界面形状及位置与真实模型完全一致.来自两个异常体的反射波聚焦较好，成像结果显示两个异常体的形态大小，空间位置与真实模型完全一致，此外偏移剖面中存在的杂波干扰较小.总体来说，逆时偏移成像效果明显好于Kirchhoff偏移结果.

逆时偏移成像算法中，初始模型的选择至关重要，初始模型的建立可以结合已知的先验信息、CMP速度分析、或者反射层析成像结果.为了研究初始模型对成像精度的影响，文中分别选取地下相对介电常数为4的均匀半空间，地下相对介电常数为6的均匀半空间以及选取全波形反演的结果作为初始速度模型.

对于共偏移距探地雷达数据，当选取地下相对介电常数为4的均匀半空间作为初始介电常数模型时，采用逆时偏移技术获得的成像结果如图6c所示，从图可知来自起伏界面的绕射波没有完全归位，杂波干扰严重，来自地下异常体的散射波能量聚焦效果较差.当选取地下相对介电常数为6的均匀半空间作为初始介电常数模型时，逆时偏移成像结果如图6d所示，来自起伏界面的反射波能量聚焦较好，能清晰的识别起伏界面的位置及形态，但是来自地下异常体的散射波能量没有完全聚焦.当选取全波形反演的结果作为初始介电常数模型时，逆时偏移成像的结果如图6e所示，从图可知，来自界面的反射波能量聚焦较好，能够清晰的识别起伏界面的形态和位置；来自地下的两个异常体的散射波能量聚焦较好，其空间位置与模型基本一致.由此可知，当初始模型越接近于真实模型时，逆时偏移成像结果越准确；全波形反演能够为逆时偏移成像提供更为准确的初始模型，将全波形反演的结果作为逆时偏移成像的初始模型是行之有效的.

对于如图3b所示的共炮点探地雷达数据，采用逆时偏移成像算法对其进行偏移成像，其结果如图6d所示，图中来自起伏界面的反射波能量得到聚焦，起伏界面的空间位置及形态与实际模型基本一致；来自地下异常体的散射波能量聚焦较好，其空间位置与模型一致.偏移剖面中，在地面处出现了若干个和源位置一致的强能量点；其反射波子波略宽于如图6b中的反射波子波宽度.

4 物理实验及数据分析

4.1 物理实验模型及数据采集

本文在实验室沙槽进行了物理模拟实验，如图7a所示，沙槽长8 m，宽1.6 m，深0.8 m，沙槽四壁为混泥土，一个PVC盒以45°倾斜角埋于沙中，其埋深约0.24 m.图7c展示的是PVC盒埋于干沙中的示意图，PVC盒厚度为0.04 m，其中间为空气，顶端位于(0.75, 0.24)m处，干沙相对介电常数是4，PVC的相对介电常数是3.1.图7b展示了本实验中采用的 MALA ProEx雷达控制单元及两套中心频率为1600 MHz的高频天线.当采集共炮点雷达数据时，雷达主机外接两个高频模块，同时将两套高频天线分别接于高频模块；当采集共偏移距雷达数据时，雷达主机外接一个高频模块，同时只需要一个高频天线.

首先用1600 MHz高频天线进行了共偏移距测量，测量过程中天线紧贴干沙表面，图8a所示是实测的共偏移距探地雷达剖面，横轴为道号，纵轴为雷达波双程走时.图中0～1 ns之间是天线耦合直达波，顶点位于3.2 ns的双曲线是来自PVC盒子顶端的散射波.同时可以发现剖面中出现了一些微弱的散射杂波，杂波是由于干沙局部不均匀性造成的.

其次，采集了共炮点雷达数据集，第一个发射天线位于起始位置，第一个接收位置距离发射天线的间距为0.1 m，每一个发射位置对应21个接收位置，即单炮雷达数据包含了21道信号，接收器间的间隔是0.01 m，发射天线的移动间距为0.05 m.图8b是实测的共炮点探地雷达数据集，它包含36个共炮点探地雷达剖面数据.这些数据将用于时间域全波形反演，以此来反演地下介质分布，从而为叠前逆时偏移成像提供初始速度模型.

4.2 雷达实测数据的全波形反演

实测数据必须经过必要的数据预处理，包括对共炮点探地雷达数据进行直流偏移和带通滤波，同时考虑到本文所用的时间域全波形反演算法是二维的，而实测雷达数据是三维的，故采用(Bleistein, 1986)提出的三维转二维技术，将三维实测数据转为二维情况下的数据，从而消除它们在幅度和相位上的差异.由于在沙中仅埋有一个PVC盒子，故而在时间域全波形反演中，采用相对介电常数为4均匀模型作为的初始相对介电常数模型(图9a).以实测雷达数据和计算雷达数据的均方根作为反演迭代次数的目标函数，如图10所示，经过15次迭代后，目标函数的误差改变小于1%.图9b是迭代15次后的相对介电常数反演结果，图中可清晰辨别出倾斜掩埋的PVC盒子，其形状和位置与实际模型基本一致，倾角也非常接近45°，此外反演结果中小散射点清晰可见.

图7 物理模拟实验(a) PVC盒子倾斜掩埋在沙中; (b) 实验用到的仪器：Mala ProEx控制单元及两套1600 MHz的高频天线;(c) PVC盒子埋于干沙中的示意图.Fig.7 Laboratory experiment setup(a) The PVC box tilted buried in sand; (b) Instruments used to carry out radar measurements consisting of Mala ProEx control unit and two sets of 1.6 GHz antenna; (c) A sketch of the PVC box embedded in sand.

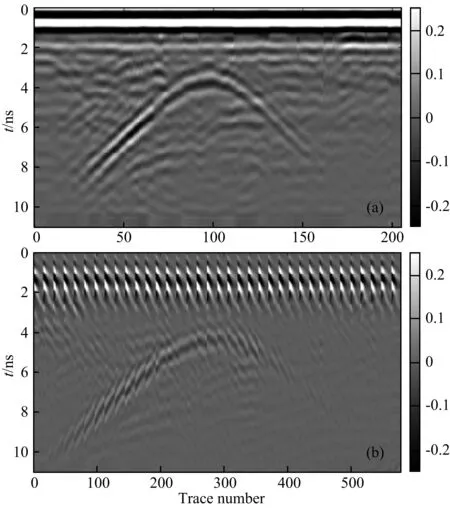
图8 物理实验实测数据(a) 实测的共偏移距剖面; (b) 实测的包含36条共炮点雷达剖面的雷达数据集，所有图像均进行了归一化.Fig.8 Physical experiments radar data(a) The measured common-offset profile; (b) The measured radar gather consisting of 36 common-shot radar profiles, all figures are normalized by their maximum amplitude.

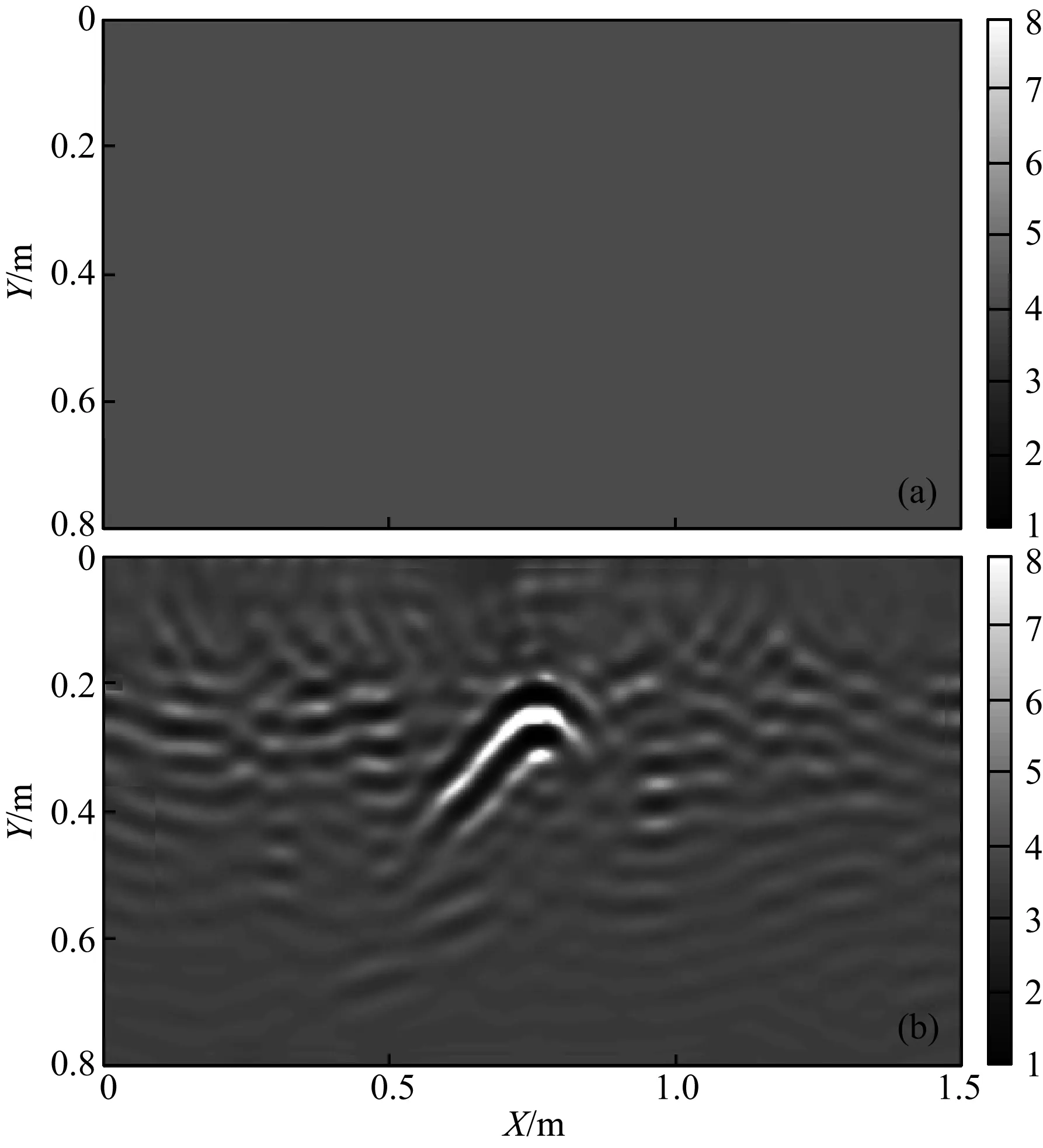
图9 FWI的初始介电常数模型(a) 相对介电常数定为4; (b) 15次反演迭代后的介电常数结果.Fig.9 The initial permittivity model for the FWI(a) The dielectric constant is set to 4; (b) The inversion permittivity results after 15 iterations.

图10 以实测雷达数据和计算雷达数据间均方根值作为迭代次数的函数(均方根值经过以做归一化，而且15次迭代后均方根改变值小于1%)Fig.10 RMS values as a function of the iteration number for the observed radar data and the calculated data (The RMS is normalized to its maximum and after 15 iterations; the RMS misfit changes less than 1%)

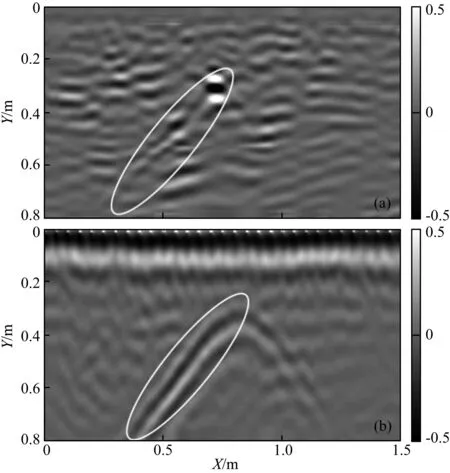
图11 (a)实测共偏移距剖面Kirchhoff偏移结果; (b)实测共炮点雷达数据得到的逆时偏移成像结果，两图均已归一化处理Fig.11 (a) Kirchhoff migration result from measured common-offset profile, (b) RTM result from measured common-shot radar gather; all figures are normalized by their maximum amplitude

4.3 探地雷达实测数据的逆时偏移结果

通过时间域全波形反演获得了地下介电常数分布情况，基于反演结果给定的初始介电常数模型，分别进行了Kirchhoff偏移成像和逆时偏移成像，其结果见图11.图11a是对实测的共偏移距雷达数据进行Kirchhoff偏移成像得到的结果，显然来自PVC盒顶的双曲线同向轴能量收敛到一个点，该聚焦点几乎与PVC盒顶端位置吻合，然而PVC盒身在偏移图像中并没有得到成像，此外，成像结果中出现了许多散射杂点，这些散射杂点不利于雷达数据的解释.图11b是对实测共炮点探地雷达数据进行逆时偏移成像处理获得的结果，从图可知，成像结果中倾斜PVC盒子整体(白色椭圆框所示)形态及倾角与实际模型基本一致，其偏移结果明显好于Kirchhoff偏移成像结果.

5 结论与讨论

本文开发了电磁波二维逆时偏移成像算法，其中电磁波场的正向传播和反向传播均采用时间域有限差分方法，互相关成像条件用于获得成像结果.考虑到全空间波场存储内存开销较大，文中将成像空间外边界做为存储空间，记录其各个时刻的场值，记录的场值完全能够恢复电磁波场的正向传播过程.

数值模拟实验中，构建了横向速度变化较大的模型，合成了共偏移距和共炮点雷达数据.对于合成的共偏移距雷达数据，同时采用Kirchhoff偏移成像和逆时偏移成像算法，对比成像结果发现，逆时偏移成像剖面中，来自起伏界面及地下异常体的空间位置和几何形态与实际模型一致，而Kirchhoff偏移剖面中来自起伏界面和异常体的反射波(散射波)能量聚焦不完全，剖面中仍然存在明显的杂波，可见逆时偏移成像算法明显好于Kirchhoff偏移算法.然而需要注意的是，逆时偏移成像算法是基于正演计算，每完成一次偏移需要进行两次以上正演计算，而正演计算非常耗时，故而其计算效率远低于Kirchhoff偏移算法.采用逆时偏移成像处理共炮点雷达合成数据，得到的成像剖面与该算法处理共偏移距雷达数据获得的成像剖面基本一致，不同之处在于前者成像剖面中的子波宽度略宽于后者.

影响逆时偏移成像效果的关键因素之一是包括介电常数和电导率在内的初始模型的选择，数值实验表明更精准的初始模型能获得更高精度的偏移成像结果.为了获得更精确的初始模型，本文通过时间域全波形反演算法对探地雷达数据进行全波形反演，反演后的地下相对介电常数模型作为逆时偏移成像的初始速度模型.数值模拟实验及实际物理模拟实验表明，通过全波形反演获取的信息作为逆时偏移成像的初始模型是行之有效的，同时逆时偏移成像的效果在一定程度上检验了全波反演结果的准确性.

Baysal E, Kosloff D D, Sherwood J W C. 1983. Reverse time migration.Geophysics, 48(11): 1514-1524.

Bleistein N. 1986. Two-and-one-half dimensional in-plane wave propagation.GeophysicalProspecting, 34(5): 686-703.

Chang W F, McMechan G A. 1986. Reverse-time migration of offset vertical seismic profiling data using the excitation-time imaging condition.Geophysics, 51(1): 67-84.

Chang W F, McMechan G A. 1994. 3-D elastic prestack, reverse-time depth migration.Geophysics, 59(4): 597-609.

Chattopadhyay S, McMechan G A. 2008. Imaging conditions for prestack reverse-time migration.Geophysics, 73(3): S81-S89.

Claerbout J F. 1971. Toward a unified theory of reflector mapping.Geophysics, 36(3): 467-481.

Docherty P C. 1991. A brief comparison of some Kirchhoff integral formulas for migration and inversion.Geophysics, 56(8): 1164-1169.

Fang N S, Ying L A. 2009. Stability analysis of FDTD to UPML for time dependent Maxwell equations.ScienceinChinaSeriesA, 52(4): 794-816.

Feng D S, Dai Q W. 2011. GPR numerical simulation of full wave field based on UPML boundary condition of ADI-FDTD.NDT&EInternational, 44(6): 495-504.Feng X, Sato M. 2004. Pre-stack migration applied to GPR for landmine detection.InverseProblems, 20(6): S99-S115.

Fisher E, McMechan G A, Annan A P, et al. 1992. Examples of reverse-time migration of signal-channel ground-penetrating radar profiles.Geophysics, 57(4): 577-586.

Gray S H. 1986. Efficient traveltime calculations for Kirchhoff migration.Geophysics, 51(8): 1685-1688.

Gray S H, May W P. 1994. Kirchhoff migration using eikonal equation traveltimes.Geophysics, 59(5): 810-817.

Guitton A, Kaelin B, Biondi B. 2006. Least-squares attenuation of reverse-time-migration artifacts.Geophysics, 72(1): S19-S23.

Guitton A, Valenciano A, Bevc D, et al. 2007. Smoothing imaging condition for shot-profile migration.Geophysics, 72(3): S149-S154. Levin S A. 1984. Principle of reverse-time migration.Geophysics, 49(5): 581-583.

Liu S X, Sato M. 2005. Transient radiation from an unloaded, finite dipole antenna in a borehole: experimental and numerical results.Geophysics, 70(6): K43-K51.

Liu S X, Zeng Z F, Xu B. 2006. FDTD simulation of ground penetrating radar signal in 3-Dimensional dispersive medium.JournalofJilinUniversity(EarthScienceEdition) (in Chinese), 36(1): 123-127.

Liu S X, Zeng Z F, Deng L. 2007. FDTD simulations for ground

penetrating radar in urban applications.JournalofGeophysicsandEngineering, 4(3): 262-267.

Liu S X, Zeng Z F.2007.Numerical simulation for Ground Penetrating Radar wave propagation in the dispersive medium.ChineseJ.Geophys. (in Chinese), 50(1): 320-326.

Liu S X, Wu J J, Zhou J F, et al. 2011. Numerical simulations of borehole radar detection for metal ore.IEEEGeosci.RemoteSens.Lett., 8(2): 308-312.

Liu X X, Yin X Y, Liu B H. 2013. Prestack reverse-time migration of elastic waves in porous media.ProgressinGeophys. (in Chinese), 28(6): 3165-3173.

Loewenthal D, Mufti I R. 1983. Reversed time migration in spatial frequency domain.Geophysics, 48(5): 627-635.

Meles G, Greenhalgh S, van der Kruk J, et al. 2011. Taming the non-linearity problem in GPR full-waveform inversion for high contrast media.JournalofAppliedGeophysics, 73(2): 174-186. Meles G A, van der Kruk J, Greenhalgh S A, et al. 2010. A new vector waveform inversion algorithm for simultaneous updating of conductivity and permittivity parameters from combination crosshole/borehole-to-surface GPR Data.IEEETransactionsonGeoscienceandRemoteSensing, 48(9): 3391-3407.

Mufti I R, Pita J A, Huntley R W. 1996. Finite-difference depth migration of exploration-scale 3-D seismic data.Geophysics, 61(3): 776-794.

Sava P, Fomel S. 2006. Time-shift imaging condition in seismic migration.Geophysics, 71(6): S209-S217.

Sun R, McMechanz G A. 2001. Scalar reverse-time depth migration of prestack elastic seismic data.Geophysics, 66(5): 1519-1527. Taflove A, Hagness S. 2005. Computational Electrodynamics - The Finite-Difference Time-Domain Method, 3rd Ed. London: Artech House.Vidale J E. 1988. Finite-difference calculation of travel times.Bull.Seismol.Soc.Am., 78(6): 2062-2076.

Wang B L, Gao J H, Chen W C, et al. 2012. Efficient boundary storage strategies for seismic reverse time migration.ChineseJ.Geophys. (in Chinese), 55(7): 2412-2421, doi: 10.6038/j.issn.0001-5733.2012.07.025.

Yoon K, Marfurt K J. 2006. Reverse-time migration using the Poynting vector.ExplorationGeophysics, 37(1): 102-107.

Yoon K, Shin C, Suh S, et al. 2003. 3D reverse-time migration using the acoustic wave equation: An experience with the SEG/EAGE data set.TheLeadingEdge, 22(1): 38-41.

Zhou H, Sato M, Liu H J. 2005. Migration velocity analysis and prestack migration of common-transmitter GPR data.IEEETransactionsonGeoscienceandRemoteSensing, 43(1): 86-91.

附中文参考文献

刘四新, 曾昭发, 徐波. 2006. 三维频散介质中地质雷达信号的FDTD数值模拟. 吉林大学学报(地球科学版), 36(1): 123-127. 刘四新, 曾昭发. 2007. 频散介质中地质雷达波传播的数值模拟. 地球物理学报, 50(1): 320-326.

刘欣欣, 印兴耀, 刘百红. 2013. 孔隙介质弹性波叠前逆时偏移方法. 地球物理学进展, 28(6): 3165-3173.

王保利, 高静怀, 陈文超等. 2012. 地震叠前逆时偏移的有效边界存储策略. 地球物理学报, 55(7): 2412-2421, doi: 10.6038/j.issn.0001-5733.2012.07.025.

(本文编辑 汪海英)

Reverse time migration applied to GPR data based on full wave inversion

LEI Lin-Lin1, LIU Si-Xin1, FU Lei1*, WU Jun-Jun2

1CollegeofGeo-explorationScienceandTechnology,JilinUniversity,Changchun130026,China2BGPInc.,ChinaNationalPetroleumCorporation,ZhuozhouHebei072751,China

Reverse-time migration (RTM) is used for subsurface imaging to handle complex velocity models including steeply dipping interfaces and dramatic lateral variations, and promises better imaging results compared to traditional migration methods such as Kirchhoff migration algorithm. RTM has been increasingly applied to seismic surveys for hydrocarbon resource explorations. Based on the similarity of kinematics and dynamics between electromagnetic waves and elastic waves, we develop a pre-stack RTM method and apply it to processing ground penetrating radar (GPR) data.The finite-difference time domain (FDTD) numerical method is used to simulate the electromagnetic wave propagation including forward and backward extrapolation. The cross-correlation imaging condition is used to obtain the final image. In order to provide a velocity model with relatively higher accuracy as the initial velocity model for RTM, we apply a full waveform inversion (FWI) in the time domain to estimate the subsurface velocity structure based on reflection radar data. For testing the effectiveness of the algorithm, we have constructed a complex geological model; and synthesized common-offset radar data and common-shot profile (CSP) radar reflection data. All data are migrated with the traditional Kirchhoff migration method and pre-stack RTM method separately. The migration results from pre-stack RTM show better coincidence with the true model. Furthermore, we have performed a physical experiment in a sandbox where a polyvinyl chloride (PVC) box is buried in the sand. The obtained common-offset radar data and common-shot radar data are migrated by using the Kirchhoff migration method and per-stack RTM algorithm separately. The per-stack RTM result shows that the RTM algorithm can obtain better imaging results.In the numerical experiments, velocity variation exists in the geological model due to the irregular interface between soil and sand. The imaging result from pre-stack RTM is better than that of the traditional Kirchhoff migration algorithm because pre-stack RTM can handle the model with horizontal velocity variation. In the RTM imaging, the shape and position of the interface and their anomalies match well with the true model, while the imaging of Kirchhoff migration cannot do so. As for the physical experiment, the Kirchhoff migration algorithm and pre-stack RTM have been applied to process the measured radar data. The imaging results from RTM show its advantage compared with the Kirchhoff migration method.

Reverse time migration; GPR; Full waveform inversion; Physical model experiment

雷林林, 刘四新, 傅磊等. 2015. 基于全波形反演的探地雷达数据逆时偏移成像.地球物理学报，58(9):3346-3355,

10.6038/cjg20150927.

Lei L L, Liu S X, Fu L, et al. 2015. Reverse time migration applied to GPR data based on full wave inversion.ChineseJ.Geophys. (in Chinese),58(9):3346-3355,doi:10.6038/cjg20150927.

10.6038/cjg20150927

P631

2014-03-14，2015-08-02收修定稿

国家自然科学基金项目(40874073,41074076),国家高技术研究发展计划项目(2013AA064603)及中石油东方地球物理公司中青年科技创新基金项目(11-06-2013)共同资助.

雷林林，女，1987年生，博士生，主要从事地球物理数据处理与正反演研究.E-mail:leilljlu@126.com

*通讯作者 傅磊，男，1985年生，讲师.E-mail:fuleijlu@163.com