一类三阶时滞微分方程的稳定性和有界性

徐 林，宋常修

(广东工业大学应用数学学院，广东广州510520)

1 问题的提出

时滞微分方程主要用来描述依赖当前和过去历史状态的动力系统，因此它在物理、信息、化学、工程、经济以及生物数学等领域都有重要应用.由于时滞微分方程在实际中应用如此广泛，所以对时滞微分方程的理论研究就显得十分重要，也是非常有意义的.对时滞微分方程的稳定性理论的研究的转折点可以追溯到1892年，这一年俄国数学家Lyapunov发表了一篇名为《运动的稳定性的一般问题》的论文，该论文给出了研究稳定性的一种很有效的方法，称为Lyapunov第二方法，它至今仍是研究时滞微分方程解的稳定性的主要方法，Lyapunov直接法的关键是构造Lyapunov泛函.至今已经有很多学者在这方面有很好的研究成果，文献［1-16］中有很多的介绍.

特别地，关于时滞微分方程解的稳定性和有界性的研究现状.

2003年，Sadek［16］研究了如下三阶时滞微分方程

得到了当p(t)=0时它的零解渐近稳定的充分条件，及p(t)≠0时它的所有解有界的充分条件.

2006年，CemilTunc［10］研究了一类三阶非线性时滞微分方程

的零解稳定的充分条件.

2007年，姚洪兴和孟伟业［4］讨论了如下三阶双滞量时滞微分方程的全局渐近稳定性

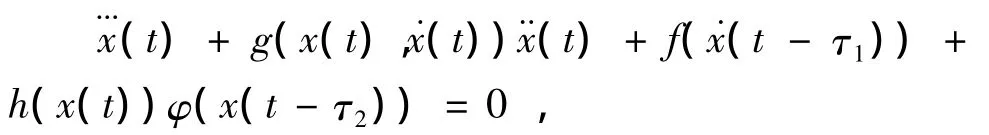
给出了其零解全局渐近稳定的充分条件.

受文献［5］的启发，本文研究了一类三阶时滞微分方程解的稳定性和有界性，给出了其零解渐近稳定和所有解有界的充分性条件.

本文研究三阶时滞微分方程

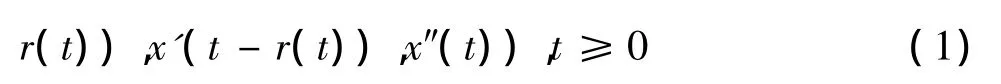
零解的渐近稳定性和所有解的有界性.其中，f(0)=h(0)=g(0，0)=φ(0)=0，0≤r(t)≤r，g(x，y)，f(x)，h(x)，φ(x)均为连续函数.

系统(1)等价于系统

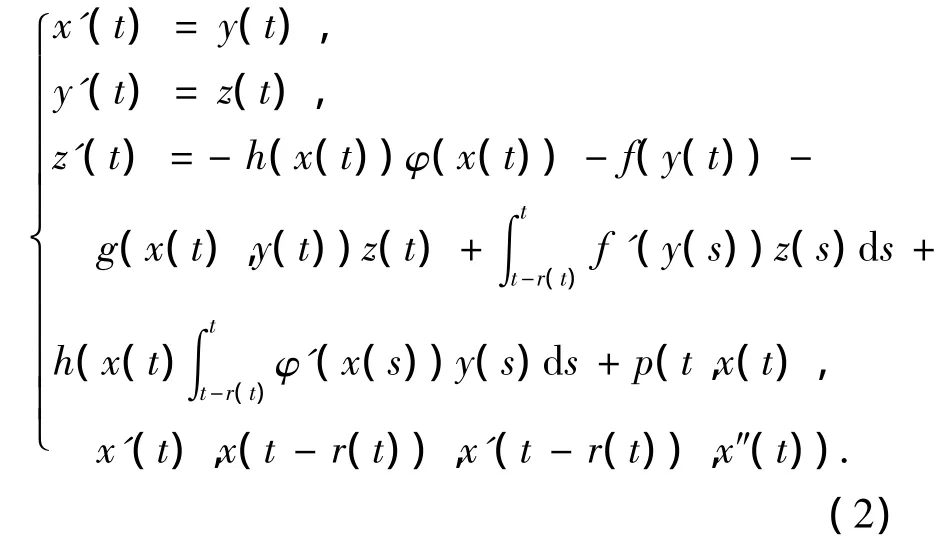
2 渐近稳定性

当p(t，x(t)，x′(t)，x(t-r(t))，x′(t-r(t))，x″(t))=0时，讨论式(1)的渐近稳定性.

考虑自治RFDE系统:

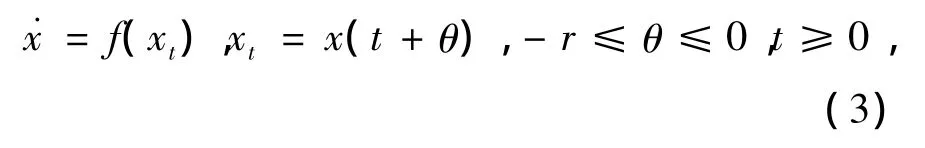
其中，f:CH→Rn是连续泛函，f(0)=0，CH={φ ∈C(［-r，0］，Rn):φ≤H}且满足对H1＜H，若Φ≤H1，则存在L(H1)＞0，使

引理1［6］令V(Φ):CH→R为满足局部Lipschitz条件的连续泛函，V(0)=0且满足下列条件:

定理1若存在正整数a，b，c，d，L，M，B且满足:

(1)0＜[h(x)φ(x])′＜ab-c;

(3)h(x)φ(x)sgnx＞0(x≠0)，对任意的x都有

(4)g′x(x，y)y≤0且g(x，y)≥a+d;

(5)0≤r(t)≤ σ，r′(t)≤ β，0＜ β ＜1，那么当

则系(1)的零解是渐近稳定的.

证明 先定义一个Lyapunov泛函V(xt，yt，zt)，

明显地，V(0，0，0)=0.

又由定理1条件(3)和(4)知h(x)φ(x)sgnx＞0，g(x，y)-a＞d.

显然，对于以上不等式，存在足够小的正常数Di(i=1，2，3)，使得

成立，则V(xt，yt，zt)正定.

因此，泛函V(xt，yt，zt)满足引理1的条件(1).

由定理1所给的条件可得

同理

又因为

则由上面不等式得

若取

因此，泛函V(xt，yt，zt)满足引理1的条件(2).

容易证明Z中最大不变集是Q={0}，在这里Z={Φ ∈CH，V′(Φ)=0}，根据

因此，引理1的所有条件都满足，所以式(1)的零解是渐近稳定的.

定理得证.

3 有界性

引理2［7］Gronwall-Reid-Bellman不等式:若u(t)与α(t)都是[a，b]上的连续函数，β(t)≥0在[a，b]上可积且成立

则必有

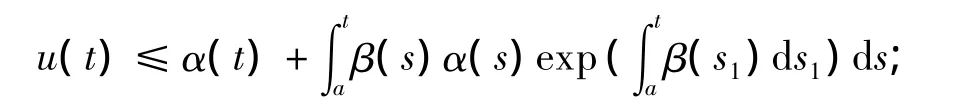
若α(t)非减，则成立

对于p(t，x(t)，x′(t)，x(t-r(t))，x′(tr(t))，x″(t))≠0的情况，有下列结论:

定理2［9］假设定理1的条件成立且连续函数p满足下列条件:

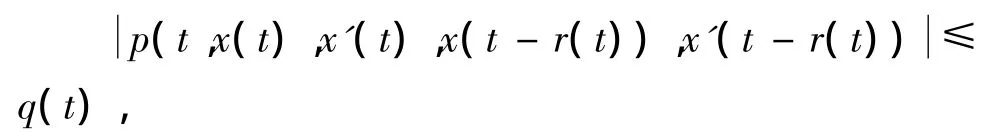
其中q(t)∈L1(0，∞)，L1(0，∞)是Lebesgue可积函数空间.

当

时，存在一个有限正常数M使系统(2)的解x(t)对所有的t≥t0满足不等式

注:这里用来证明定理2的Lyapunov函数V(xt，yt，zt)与定理1相同.

证明 对于p(t，x(t)，x′(t)，x(t-r(t))，x′(t-r(t))，x″(t))≠0的情况，有

其中D7=max{1，a}.

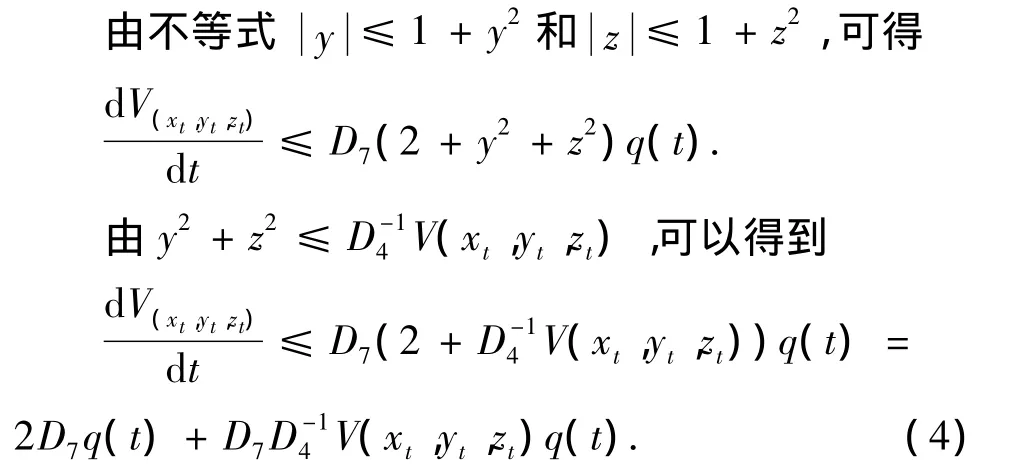
对式(4)从0到t进行积分，并利用假设q∈L1(0，∞)和Gronwall-Reid-Bellman不等式，可得

其 中M1是 正 常 数，M1=(V(x0，y0，z0)+所以

其中M=D-14M1.

因此，当t≥t0时，不等式成立.

即当t≥t0时成立.

证毕.

例题1考虑三阶时滞微分方程

方程(5)可表示为如下系统

令

显然方程(5)是式(1)的特殊形式，可知

由于

则

其中q∈L1(0，+∞).

因此定理1和定理2的所有条件都成立，当p≡0时方程(5)的零解渐近稳定，当p≠0时方程(5)所有解有界.

［1］王联，王慕秋.非线性常微分方程定性分析［M］.哈尔滨:哈尔滨工业大学出版社，1987.

［2］王琦.标量随机延迟微分方程Euler-Maruyama方法的均方稳定性分析［J］.广东工业大学学报，2011，28(1):50-53.Wang Q.Mean-square stability analysis of euler-maruyama method for scalar stochastic delay differential equations［J］.Journal of Guangdong University of Technology，2011，28(1):50-53.

［3］王联，王慕秋.一类三阶非线性系统李雅普洛夫函数构造分析［J］.应用数学学报，1983，6(3):309-323.Wang L，Wang M Q.On the construction of globally asymptotically stable lyapunov’s of a type of nonlinear third-order systems［J］.Applied Mathematics，1983，6(3):309-323.

［4］姚洪兴，孟伟业.一类三阶双滞量时滞微分方程的全局渐近稳定性［J］.应用数学，2008，21(3):576-580.Yao H X，Meng W Y.Global asymptotic stability of a class of third-order differential equation with two delays［J］.Mathematics Applied，2008，21(3):576-580.

［5］Tunc C.On the stability of solutions to a certain fourth-order differential equation［J］.Nonlinear Dyn，2008，51(1-2):71-81.

［6］Yao H X，Meng W Y.On the stability of solutions of certain non-linear third-order delay differential equations［J］.International Journal of Nonlinear science，2008，6(3):230-237.

［7］张丽娟，斯力更.一类三阶非线性系统的全局稳定性［J］.应用数学学报，2007，30(1):99-103.Zhang L J，Si L G.The whole stability of a class of third order nonlinear system［J］.Applied Mathematics，2007，30(1):99-103.

［8］傅朝金，廖晓芹.时滞微分方程的稳定性［J］.数学物理学报，2003，23A(4):494-498.Fu C J，Liao X Q.Stability for differential equations with delay［J］.Acta Mathematica Scientia，2003，23A(4):494-498.

［9］赵杰民.一类非线性时滞系统的定性分析［J］.数学杂志，2000，20(4):403-409.Zhao J M.Qualitative analysis for a class of nonlinear delay system［J］.J.of Math，2000，20(4):403-409.

［10］Tunc C.New results about stability and boundedness of certain non-linear third-order delay differential equations［J］.The Arabian Journal for Science and Engineering，2006.31(24):185-196.

［11］朱元峰.一类二阶和三阶时滞微分系统的稳定性［J］.中国科学院研究生院学报，1990，7(2):10-17.Zhu Y F.On thestability of a type of second and third order delay differential systems［J］.Journal of Graduate School，1990，7(2):10-17.

［12］贾建文.一类三阶非线性系统的全局稳定性的Lyapunov函数的构造［J］.应用数学学报，1999，22(4):621-623.Jia J W.On the construction of globally asymptotically stable lyapunov’s of a type of nonlinear third-order systems［J］.Applied Mathematics，1999，22(4):621-623.

［13］刘昌东.一类三阶非线性微分方程的全局渐近稳定性［J］.湛江师范学院学报:自然科学版，1999，20(2):16-18.Liu C D.The entire gradual stability of a class of third order nonlinear differential Equation［J］.Journal of Zhanjiang Normal College:Natural Sciences Edition，1999，20(2):16-18.

［14］Zhu Y.On stability，boundedness and existence of periodic solution of a kind of third-order nonlinear Delay differential system［J］.Ann of Diff Eqs，1992，8(2):249-259.

［15］Tunc C.On the stability of solutions of certain fourth-order delay differential equation［J］.Applied Mathematics，2006，27(8):1141-1148.

［16］Sadek A I.Stability and boundedness of a kind of third-order differential system［J］.Applied Mathematics Letters，2003，16(5):657-662.