基于万有引力思想的遗传算子

李松芳，刘 伟

(广东工业大学应用数学学院，广东广州510006)

遗传算法是一种有效的智能优化算法，它主要借鉴生物学中的生物进化理论.经过几十年的发展，遗传算法以其简单、可操作性强、鲁棒性强和潜在的并行性特点，被应用于工业工程的诸多领域［1-4］.同时，传统遗传算法也暴露出易进入局部最优和随机波动等现象，导致算法的性能较差.一般情况下，算法要达到更高的收敛精度，需要增加较长的搜索时间，这些因素影响了遗传算法的发展和实际应用［4-7］.

如何克服遗传算法的不足，一直都是研究的热点.其中，遗传算子的改进是一个重要方面:Jong De K A［7］针对单点交叉提出了多点交叉.Kusum Deep和Manoj Thakur［8-9］成功把高斯分布引入交叉算子，以及把指数分布引入变异算子.Eshelman L J等［10］人提出了混合杂交，混合杂交在由父代构成的超三角内随机得到后代.Janilow和Michalewicz Z［11］提出了非均匀变异，提高了算法的搜索精度和微调能力.Gen等［12］提出了有向变异，有效避免了个体陷入局部最优.另一个人们关注的研究方向是混合遗传算法:文献［13］将爬山算子引入遗传算法，提出了基于爬山算子和适应值共享的改进遗传算法，有效地提高了遗传算法的局部搜索能力.文献［14］将局部搜索算子嵌入遗传算法形成局部搜索块，为解决遗传算法局部搜索能力差，提供了一种有效的方法.上述文献从不同的方向出发对遗传算法做出了有效改进，增强了算法的收敛速度和提高了解的精度.

在种群进化过程中，最优个体往往代表着算法的迭代方向，能否挖掘并充分利用最优个体的特征信息，对算法的搜索性能具有至关重要的影响［15-20］.为此，本文借鉴万有引力搜索算法［21-23］和混沌搜索对算术交叉和非均匀变异算子进行了改进，得到了一种改进的遗传算法(Gravitational Search Genetic Algorithm，GSGA).改进交叉算子对进入交叉运算的每两个个体利用万有引力搜索算法中个体的运动法则，在两个个体互相的引力作用下，质量较大的个体运动速度较慢，质量较小的个体运动速度较快，从而质量较小的个体向质量大的个体靠拢，同时本文将进入交叉运算的个体和最优个体进行交叉，这样在一定程度上有效利用了最优个体信息，达到提高收敛速度的效果;在改进的变异算子中，在种群每个个体的引力作用下，进入变异的个体以及最优个体在合力作用下在一定范围内搜索，有利于算法在探索新区域的同时，也增强了算法的收敛精度.

1 GSGA算法思想

1.1 改进的交叉算子

算术交叉算子是由凸集理论得来.一般，两个个体X1和X2经过算术交叉得到的个体X′1和X′2为

本文对交叉算子改进为

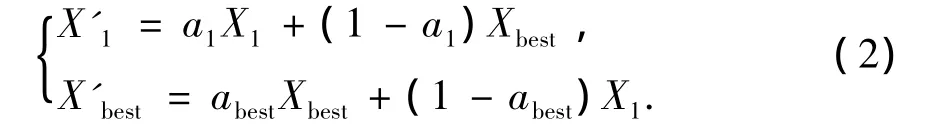
其中Xbest为种群最优个体，a1为X1在Xbest作用下的加速度.

计算主要依据万有引力搜索算法，该算法根据牛顿万有引力定律——宇宙内随机两个质点之间存在吸引力F，该引力的大小与它们的质量M1和M2的乘积成正比，与它们之间的距离R的平方成反比(其中G为引力常数)

以及牛顿运动定律——质点的运动加速度a等于该质点所受的力F和其质量M的比值

由N个个体构成的种群表示为

X={X1，X2，…，Xi…，XN}，其 中Xi=

其中G(t)是第t代下的万有引力常量，Maj(t)是个体Xj的主动引力质量，Mpi(t)是个体Xi的被动引力质量.Rij(t)表示个体Xi和Xj之间的距离(i和j为个体排序后的位置序号)，定义如下:

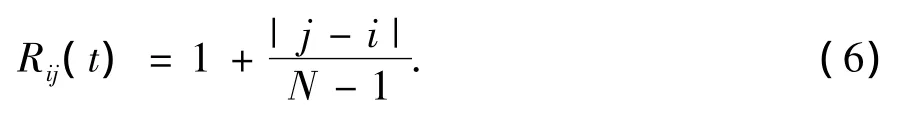
Rij(t)由个体Xi和Xj在种群的位置进行定义，当个体Xi和Xj的适应值相差越小，即|j-i|越小，则Rij(t)越小.

万有引力常量初始值为G0(本文G0=1)，随着t的增加，G会逐渐减小来控制搜索的精确度.G是关于G0和t的函数(T为迭代次数).

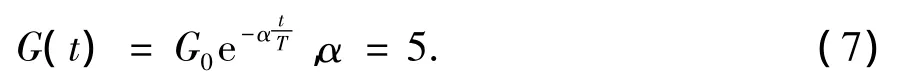
引力质量和惯性质量通过适应值函数计算得到，假设引力质量和惯性质量相等，新个体的引力质量和惯性质量定义为

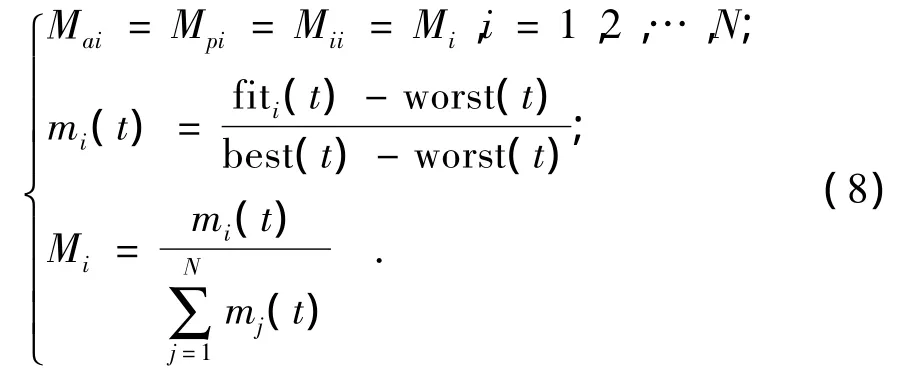
其中，fiti(t)表示个体Xi在第t代的适应值，best(t)和worst(t)定义为

ai表示个体Xi受到个体Xj作用后的加速度，计算如下:

1.2 改进的变异算子

非均匀变异算子是由Michalewicz［24］提出的.该算子可以得到较高的计算精度而且具有微调能力.

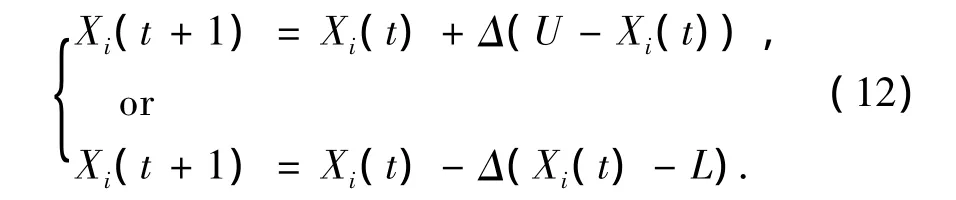
其中［L，U］表示Xi的可行区间，Δ为进化代数t和y的函数，

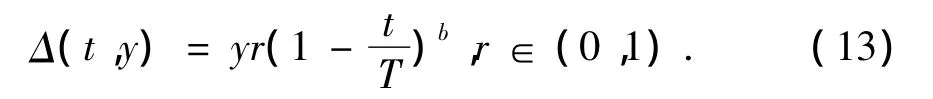
其中b是确定的非均匀程度的参数，T为进化的最大代数.

本文对变异算子改进为

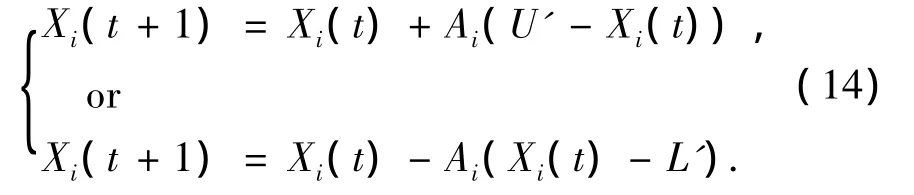
其中Ai为Xi在种群中合力作用下的加速度，由(13)式得到.［L′，U′］定义如下:

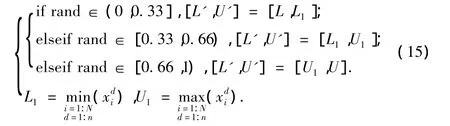
其中N为种群规模，n为个体维数，［L′，U′］为集合{［L，L1］，［L1，U1］，［U1，U］}中任意一个元素.

个体Xi在第t代受到其他个体的合力Fi(t)表示为

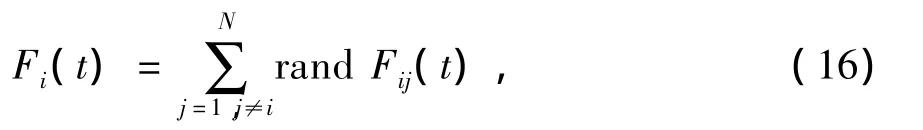
其中，rand∈［0，1］为随机数，增加算法的随机性.

Ai表示个体Xi受种群合力产生的加速度:

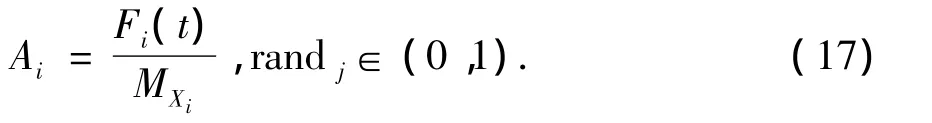
以Ackley＇s Function为例，1000代内X1和X2作用力变化和X1受种群合力变化如图1所示.

图1 个体Xi受个体Xj作用的加速度ai和受种群作用的加速度Ai的变化曲线Fig.1 Curves of aiacceleratied by Xiunder the action of Xjand Aiaccelerated by Xiunder the action of the population

由图1可知:

(1)个体的两种加速度都是在区间［0，1］内变化的.而且加速度都随着代数的增加，总体趋向于0.

(2)a∈(0，1)满足算术交叉的条件;A的变化趋势和非均匀变异参数的变化趋势相似.

(3)两个个体之间的作用力和个体在种群中受到的合力在进化前期数值较大，而且波动较大，这样有助于算法进行全局搜索，防止算法陷入局部最优;后期数值较小，有利于算法进行局部搜索，提高算法的收敛精度.

1.3 最优个体搜索策略

本文在变异运算过程中，让当代最优个体Xbest进行变异，变异运算按下式计算:

式中Ak由式(19)得到

其中Abest为个体Xbest在种群中所受的合力，k为进入变异运算个体的数目，Ak利用混沌策略进行更新.在变异运算过程中Xbest将产生k个后代.

1.4 改进的交叉算子和变异算子特点

改进后的交叉算子和变异算子主要有以下几个特点:

(1)进入交叉运算的个体都会和当代最优个体进行交叉.依据交叉算子的特点可以得到，后代个体有较大概率向最优个体运动，有利于加快种群的收敛速度.与传统算术交叉算子相比，改进的交叉算子在保持传统算术交叉的随机性的同时引入了两个父代的自身信息，使得进化更具有目的性.

(2)改进后的变异算子，继续保持了非均匀变异算子的特性，在进化前期能够进行全局搜索，后期能够进行局部搜索.在进化过程中，进入变异的个体的搜索区间给细分为3个部分，目的在于使搜索区间随着种群进化的过程，也同时进化;同时最优个体也会在变异过程中进行混沌搜索，利用混沌的遍历性、随机性的特点以及最优个体信息，从而加强的算法的局部搜索能力以及跳出局部最优解的能力.

(3)交叉变异过程中，个体的适应值越好，个体的质量就越大.在万有引力作用下，质量小的个体以大概率事件向质量大的个体靠拢.

1.5 最优个体与随机选取个体交叉与随机两个个体交叉的对比

为了说明本文提出算子的有效性，通过下面实验结果说明最优个体进入交叉运算对种群进化过程的影响.以RGA为例，在1000代内种群进化结果对比，解空间分布情况如图2和图3所示:

图2 1000代内最优个体不参与遗传运算得到的解分布Fig.2 Distribution of 1 000 intragenerational solutions of the Genetic Algorithm without best individuals

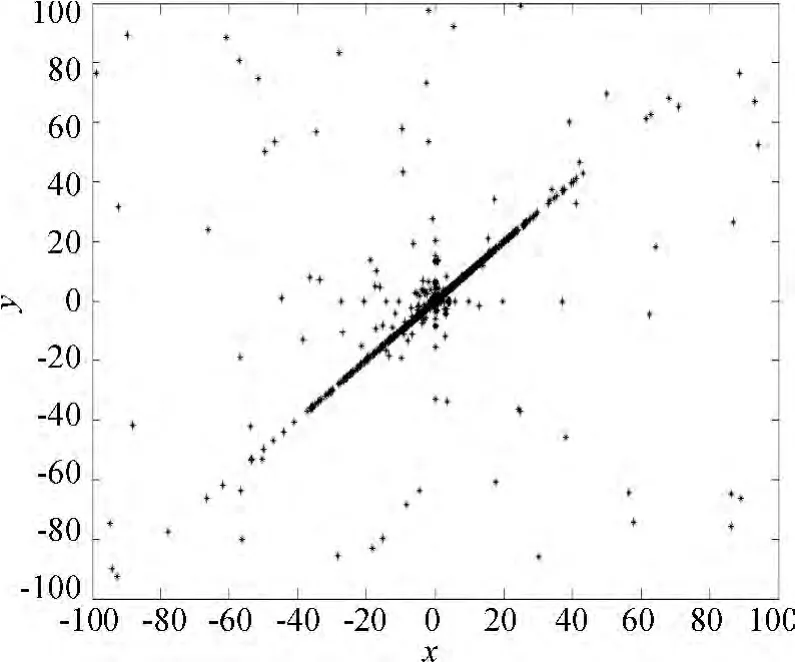
图3 1000代内最优个体参与遗传运算得到的解分布Fig.3 Distribution of 1000 intragenerational solutions of the Genetic Algorithm with best individuals

由图2和图3的对比可以得到下面结论:

(1)在最优个体不参与遗传运算的图2中，解很长时间无法集中到一个固定区域，即无法快速收敛到最优解.

(2)在最优个体参与遗传运算的图3中，解能够在较短时间集中到一个固定区域，而且汇聚到一个较小的区域，即可以快速收敛到最优解.

(3)在最优个体参与下，传统的RGA算法，可以以更快的速度收敛到最优解，而且解的精度也进一步得到提高.由此得到，最优个体在遗传算法收敛效果方面起到至关重要的作用.

2 算法流程

优化问题一般描述为:

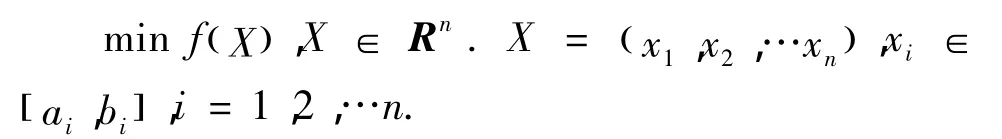
GSGA算法流程为:

Step1:参数初始化.设定种群规模N、问题的维数n、进化代数t、最大进化代数T、变量的范围［L，U］、杂交概率Pc和变异概率Pm.

Step2:种群初始化P(0):P(0)=L+rand(N，n)(U-L).其中rand∈(0，1)之间的随机数.

Step3:计算种群个体的适应值，依据适应值对个体进行排序，把最优个体记为Xbest，计算个体的质量Mi，任两个个体间的距离Rij和作用力Fij，个体受种群中所有个体的作用力的合力Fi.

Step4:按式(2)定义的交叉算子进行交叉运算.

Step5:按式(14)和(17)定义的变异算子进行变异运算.

Step6:锦标赛选择新种群，竞赛规模设置为2.

Step7:如果t≤T，t=t+1，返回Step3，否则运算结束.

3 数值实验

本文选择了8个经典的测试函数优化问题测试了3种算法的性能.

以上8个函数中，F1、F2、F6、F7为多峰独立函数，F3、F5、F8为单峰函数，F4都为多峰非独立函数.分别用文献［6］标准遗传算法(RGA)和文献［17］的万有引力搜索算法(GSA)与本文的算法(GSGA)进行比较.为了比较更有针对性，RGA采用算术交叉，非均匀变异，竞赛法选择.设置参数为:最大代数为1 000代，交叉率为0.8，变异率为0.1，种群规模为50，染色体长度为30.试验结果见表1.

表1 RGA GSA GSGA分别对F1-F8单独优化50次的结果Tab.1 RGA GSA GSGA Respectively on F1-F8to separate the result of optimization of 50 times

为了比较这些算法的收敛速度，以一次测试结果作为收敛结果，得到的收敛曲线如图4所示.

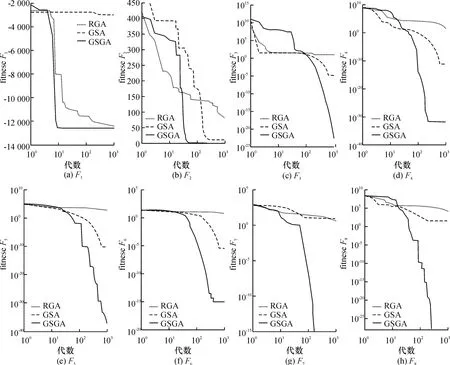
图4 各函数3种遗传算法的进化曲线Fig.4 Evolution curve of three genetic algorithm of F1～F8

从表1可以看出在相同代数内，GSGA得到的最优解要比RGA和GSA得到的最优解要好，从平均值和方差方面可以看出GSGA的稳定性要强于RGA和GSA.

从图4可以得到GSGA不仅能以比RGA和GSA更快的速度逼近最优解，而且逼近最优解的程度也是3种算法中最高的.

GSGA算法的进化曲线能够在100代内快速逼近最优解，说明算法有较强的全局搜索能力.从函数F5和函数F8后期的进化曲线可以看出GSGA算法有跳出局部最优解的能力.

4 结论

本文提出一种基于万有引力搜索的改进遗传算法(GSGA)，改进了交叉和变异算子.改进后的算子吸收了万有引力搜索优点，使之具有较强的全局及局部寻优能力，同时较好地利用了每代中最优个体的信息，从而保证了新算子具有较高的全局寻优能力.通过8个测试函数优化结果表明GSGA比GSA和RGA的寻优效果好，收敛速度快.

［1］Tu C Y，Zeng Y J.A new genetic algorithm based upon globally-optimal choosing and its practices［J］.Engineering Science，2003，5(2):28-29.

［2］Zhao C X，Ji Y M.Particle swarm optimization for 0/1 knaps problem［J］.MicrocomputerDevelepment，2005(10):23-25.

［3］张军，詹志辉.计算智能［M］.北京:清华大学出版社，2009.

［4］周明，孙树栋.遗传算法原理及其应用［M］.北京:国防工业出版社，1999.

［5］Brindel A.Genetic algorithms for function optimization［D］.Edmonton University of Alberta，Department of Computing Science，1981.

［6］Back T.The interaction of mutation rate，selection and selfadaption within a genetic algorithm［C］∥Parallel Problem Solving from Nature 2.Amsterdam［S.l.］:Elseriver Science Publisher，1992:85-94.

［7］Jong De K A.An analysis of the behavior of a class of genetic adaptive systems［D］.Ann Arbor:University of Michign，College of Literature，Science，and the Arts Computer and Communication Sciences Department，1975.

［8］Deep K，Thakur M.A new mutation operator for real coded genetic algorithms［J］.Applied Mathematics and Computation，2007(193):211-230.

［9］Deep K，Thakur M.A new crossover operator for real coded genetic algorithms［J］.Applied Mathematics and Computations，2007(188):895-911.

［10］Eshelman L J，Schaffer J D.Real-coded genetic algorithms and intervalschemata［J］.Foundation of Genetic Algorithns，1993(2):187-202.

［11］Michalewicz Z.Genetic algorithm+data structure=evolution programs［M］.New York:Springer-Verlag，1996.

［12］Gen M，liu B，Ida K.Evolution Program for deterministic and stochastic optimization［J］.European Journal of Operational Research，1996，3(94):618-625.

［13］涂井先，刘伟.基于爬山算子和适应值共享的改进遗传算法［J］.广东工业大学学报，2011，28(1):78-81.Tu J X，Liu W.An improved genetic algorithm based on mountain-climbing operators and fitness sharing［J］.Journal of Guangdong University of Technology，2011，28(1):78-81.

［14］彭伟，卢锡城.一种函数优化的混合遗传算法［J］.软件学报，1999，8(10):819-823.Peng W，Lu X C.A hybrid genetic algorithm for function optimization［J］.Journal of Software，1999，8(10):819-823.

［15］Rudoph G.Convergence analysis of canonical genetic algorithms［J］.IEEE Transaction Neural Netwoks，1994，5(1):96-101.

［16］Dinabandhu B，Murthy C A.Genetic algorithm with elitist model and its convergence［J］.International Journal of Pattern Recognition and Artificial Intelligence，1996，10(6):990-995.

［17］彭宏，王兴华.具有Elitist选择的遗传算法的收敛速度估计［J］.科学通报，1997，42(2):144-147.Peng H，Wang X H.Convergence speed estimate of genetic algorithm with elitist selection［J］.Chinese Science Bulletin，1997，42(2):14-147.

［18］谭跃，谭冠政，胡塞纯，等.自适应策略的混沌局部搜索遗传算法［J］.计算机与数字工程，2010，38(5):19-21.Tan Y，Tan G Z，Hu S C，et al.Chaotic local search genetic algorithm with adaptive strategy［J］.Computer＆Digital Engineering，2010，38(5):19-21.

［19］唐焕文，秦学志.实用最优化方法［M］.3版.大连:大连理工大学出版社，1999.

［20］董文永，张文生，于瑞国.求解组合优化问题伊藤算法的收敛性和期望收敛速度分析［J］.计算机学报，2011，34(4):636-646.Dong W Y，Zhang W S，Yu R.Convergence and runtime analysis of ITO algorithm for one class of combinatorial optimization［J］.Chinese Journal of Computers，2011，34(4):636-646.

［21］Rashedi E，Nezamabadi-Pour H，Saryazdi S.GSA:a gravitational search algorithm［J］.Information Sciences，2009，13(179):2232-2248.

［22］Sarafrazi S，Nezamabadi-Pour H，Saryazdi S.Disruption:a new operator in gravitational search algorithm［J］.Scientia Iranica，2011，3(18):539-548.

［23］Naji H R，Sohrabi M，Rashedi E.A high speed and performance optimization algorithm based on gravitational approach［J］.Computing in Science＆Engineering，2012，5(14):56-62.

［24］Michalewicz Z，Janikow C Z，Krawczyk J B.A modified genetic algorithm for optimal control problems［J］.Computers and Mathematics with Applications，1992，23(12):83-94.