扰动奇异时滞大系统鲁棒镇定

梁瑞时，金朝永

(广东工业大学应用数学学院，广东广州510006)

在许多工程中，对非线性奇异系统建立精确模型较为困难，可能性较小，因此，研究非线性系统的控制问题有重要的意义.

研究有界扰动时滞大系统的鲁棒镇定较多，但对于非线性奇异系统的研究则较少，文献［1］研究了不确定线性时变时滞系统相关状态反馈鲁棒镇定问题，基于积分不等式，引入线性化处理思想，获得了镇定控制设计准则.其研究的系统是线性且非奇异;文献［2］研究了带有非线性扰动的非脆弱奇异时变时滞系统，研究了其非脆弱保性能控制问题，利用lyapunov稳定性理论和LMI方法，得出了保性能控制律存在的充分条件和设计方法，其研究的系统是非脆弱性，不具一般性;文献［3-4］对于奇异系统的研究取得了相当的成果，使其在实际的工业中有重要的应用;文献［5-7］则讨论了一类线性时滞时变系统的鲁棒控制问题，采用状态反馈方法，得到了状态反馈控制与扰动的界关系不大，其研究的系统是线性的且非奇异.文献［8］则利用状态反馈保性能控制器的以及指标上界的方法来研究奇异时滞系统的鲁棒控制问题.

本文在文献［7-8］的讨论基础上，推广了他们对于一类非线性奇异系统的鲁棒镇定问题的研究方法，在非线性扰动条件下，设立合适的Lyapunov泛函以及鲁棒控制器，求得该系统的稳定条件，使用LMI方法结合黎卡提方程方法来求得较小的增益矩阵来证明系统的稳定，解决了系统的奇异性问题，使其具有更普遍的适应性.

1 问题描述

考虑以下状态方程

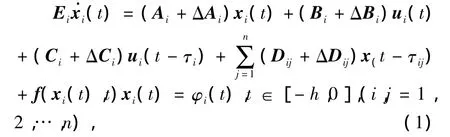
其中，Ei∈Rni×ni是奇异矩阵，并且rank(Ei)=ri＜ni;xi(t)∈Rni，ui(t)∈Rmi分别是系统的状态向量和控制输入向量，Ei，Ai，Bi，Ci，Di，Dij为具有适当维数的常数矩阵，ΔAi，ΔBi，ΔCi，ΔDij为系统的时变不确定矩阵，表示系统模型中的参数不确定性;τi，τij(i，j=1，2，…，n)分别表示系统的控制输入时滞和关联时滞，φi(t)为给定初始向量值连续函数，f(xi(t)，t)是非线性扰动，且满足f(xi(t)，t)≤η2xi(t)，η为常数.

对于系统(1)，笔者作出假设为

假设1系统中的不确定矩阵有如下限制

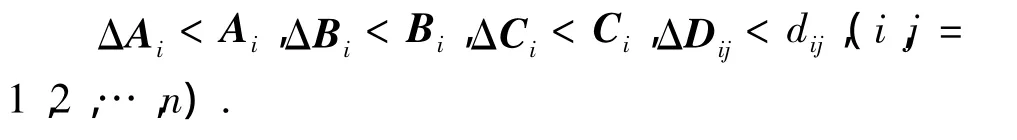
本文要用到以下引理.

引理1［9］(Schur补引理)对于对称矩阵s=，其中s12=.下面3个条件等价:

引理2［12］对适当维数的任意矩阵X和Y，有

引理3［11］对于任意的X，Y∈Rn和标量σ，有

其中，σ是正的标量.

引理4［12］若 ΔA≤ σ，则(ΔA)T(ΔA)≤ σ2.

对于奇异时滞系统

若存在矩阵Pi∈Rni×ni和正定矩阵Qi∈Rni×ni满足，则对任意满足相容性初始条件的函数φi(t)有唯一连续的解，且零解渐近稳定.

对给定的奇异时滞大系统(1)，设计鲁棒控制器

使得对于系统容许的不确定性，闭环系统

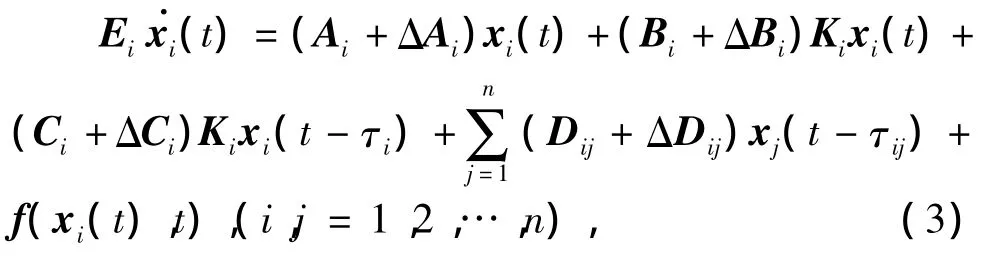
鲁棒渐近稳定.

2 结论与证明

定理1在假设的条件下，若存在正常数ξ1i、ξ2i、ξ3i、ξ4i、ξ5i，(i=1，2，…，n)和常数矩阵Ki，Ki∈Rni×ni，使得Riccati矩阵不等式

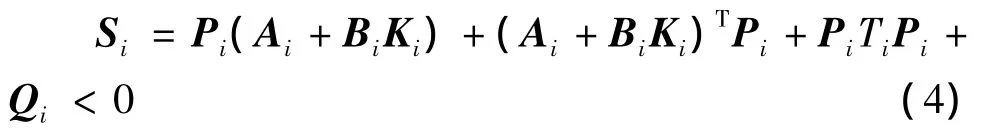
有对称正定解Pi(i=1，2，…，n).则采用鲁棒控制器(2)时，系统(1)的闭环系统(3)是鲁棒渐近稳定的.其中

证明 由于Pi＞0，取lyapunov函数为

由于Gi＞0，所以V(xi(t))正定.

沿闭环系统的轨线，V(xi(t))关于时间的导数是

由假设2，式(5)可等于

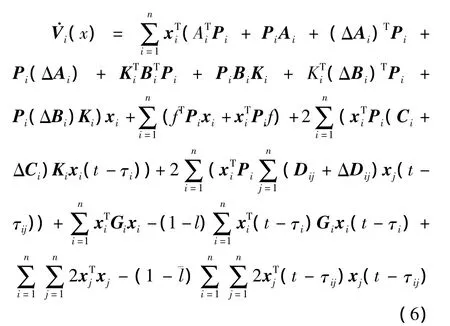
由f(xi(t)，t)≤ η2xi(t)可 推 出fT(xi(t)，

并且由引理2～4对式(6)中的各个小项进行估计得

结果，并没有多少工作可让我干。民众既安静又顺从，他们的恐慌在很久以前就消耗光了。我分发创可贴，给他们开安眠药和救急喷雾剂，后者是村子里的药剂师从一只行李箱里拿出来的。

其中Hm是对称矩阵(ΔAi)(ΔAi)T的最小上界［14］.

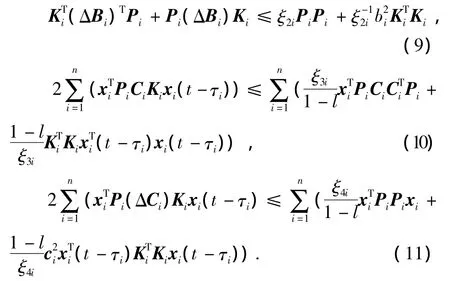
由式(10)、(11)得

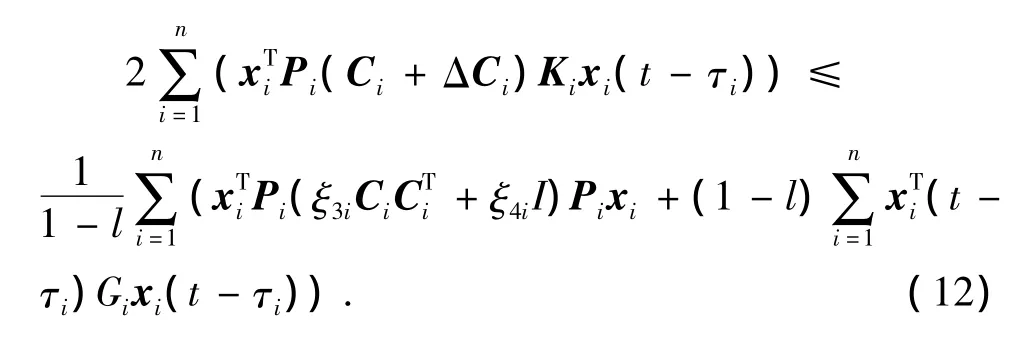
在引理3中令σ=1，则

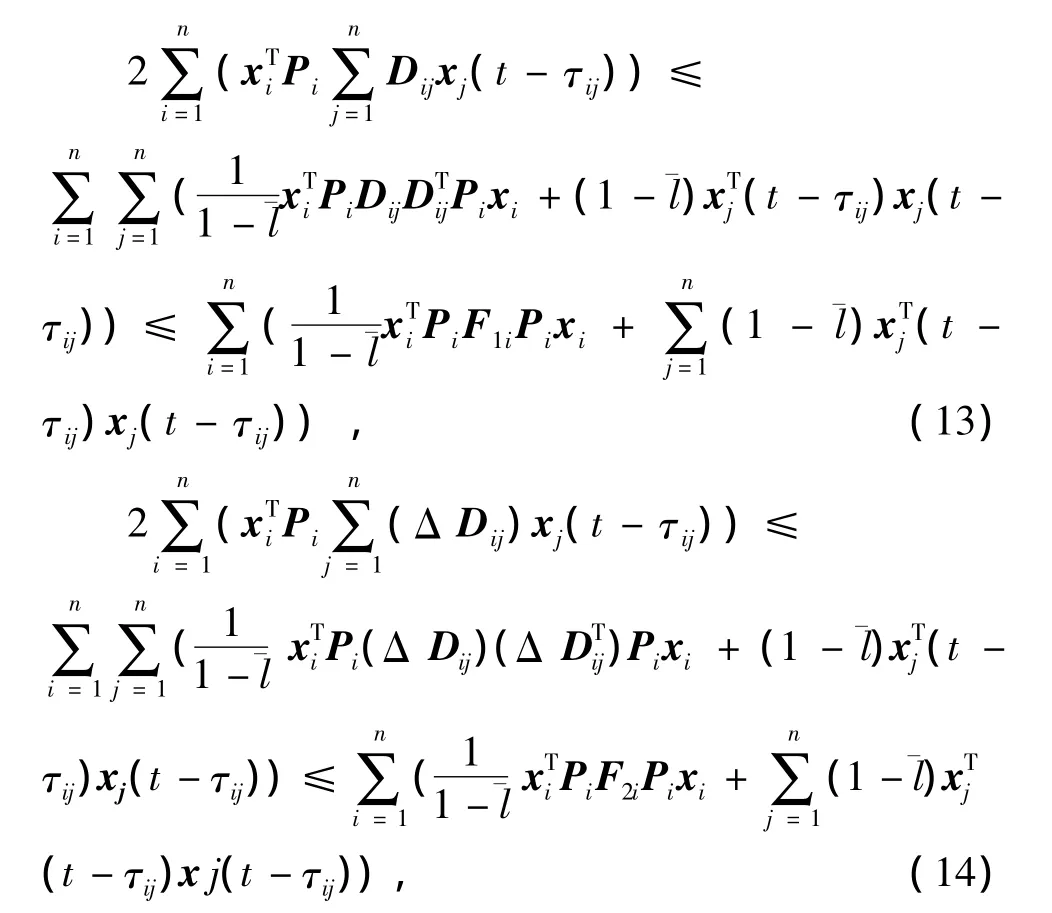
由式(13)、(14)可得

将上面所求得对应的各式代入(6)可得:

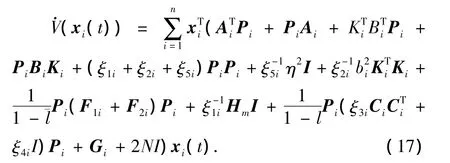
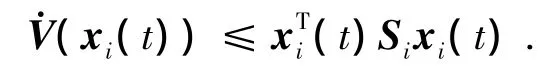
证毕.

定理2在假设1，2的条件下，给定常数Ai＞0，Ci＞0，如存在正定矩阵xi，矩阵Yi，正常数 ξ1i、ξ2i、ξ3i、ξ4i、ξ5i，(i=1，2，…，n)使得

成立，其中

则采用鲁棒控制器(2)时，系统(1)的闭环系统(3)是鲁棒渐近稳定的，且鲁棒增益阵可取为:Ki=

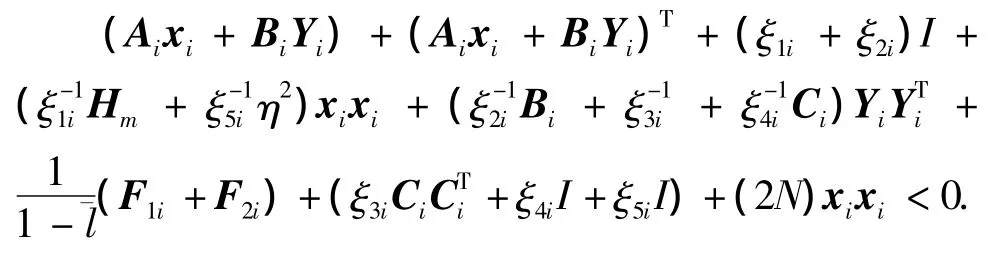
令

显然W22i＜0，矩阵(16)可变为

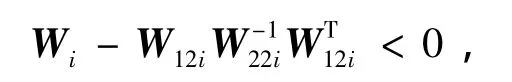
上面所求得的控制器对保证尽可能小反馈增益阵比较困难，为得到较优的增益阵，考虑成立，即0，［15］因此，较小的增益阵可由求得，其约束条件为式(18)与(19).

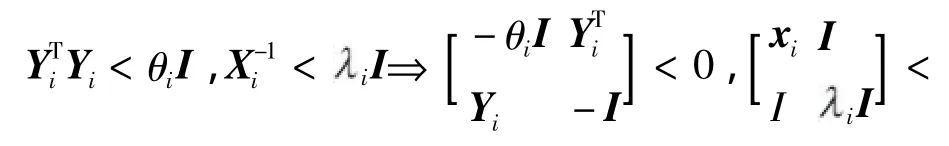
3 数值仿真

考虑系统(1)，其中:

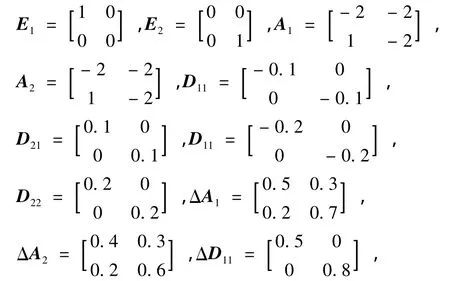
取a1=a2=c1=c2=1，γ1=γ2=0.3，则可求得

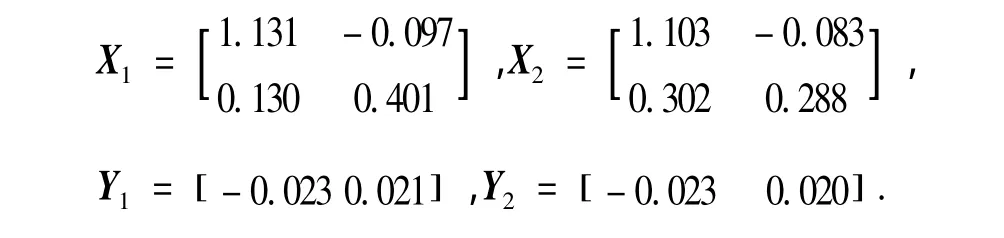
ξ11=0.815，ξ21=0.313，ξ31=15.01，ξ41=0.439，ξ51=9.487，ξ12=0.700，ξ22=0.397，ξ32=12.689，ξ42=则给出控制输入为u1(t)=［－0.0150.056］x1(t)，u2(t)=［－0.0140.084］x2(t).系统状态随时间变化曲线如图1所示.

图1 系统状态随时间变化图Fig.1 Charts of system state by on time variation

4 结束语

本文主要研究在扰动的情况下奇异时滞大系统的鲁棒渐近稳定性问题，对于数值界不确定奇异时滞大系统，给出分散鲁棒控制器，用黎卡提方程以及LMI方法相结合，证明该系统的稳定性，并通过一定的约束条件可以得到较小的增益阵，用LMI工具软件求解，该求解方法应用方便，而且有效.

［1］肖乐，伞冶，朱弈.不确定性时滞系统时滞相关状态反馈鲁棒镇定［J］.系统工程与电子技术，2013，35(4):802-806.Xiao L，San Y，Zhu Y.Delay-dependent robust stabilization by states feedback for linear systems with uncertainties［J］.Systems Engineering and Electronics，2013，35(4):802-806.

［2］尚阿曼，吴保卫，刘丽丽.带有非线性扰动的非脆弱奇异时变时滞系统的保性能控制［J］.陕西科技大学学报，2012，30(2):94-99.Shang A M，Wu B W，Liu L L.Non-fragile guaranteed cost control for a class of uncertain singular time-varying delay systems with nonlinear perturbation［J］.Journal of Shanxi University of Science＆Technology，2012，30(2):94-99.

［3］李文姿.不确定非线性时滞奇异系统的鲁棒稳定控制器设计［J］.云南师范大学学报，2012，32(5):48-51.Li W Z.Design of the robust stabilization controller for uncertain non-linear singular systems with time-deIay［J］.Journal of Yunnan Normal University，2012，32(5):48-51.

［4］齐春燕.不确定时滞奇异系统基于PD观测器的鲁棒控制［J］.湛江师范学院学报，2011，32(6):47-50.Qi C Y.PD observer-based robust control for uncertain time-delayedSingular systems［J］.Journal of Zhanjiang Normal College，2011，32(6):47-50.

［5］付主木，高爱云，费树岷.不确定切换时滞奇异系统的鲁棒H∞控制［J］.控制工程，2012，19(3):399-402.Fu Z M，Gao A Y，Fei S M.Robust H∞control for uncertain switched singular systems with stateDelay［J］.Control Engineering of China，2012，19(3):399-402.

［6］高在瑞，纪志成.一类切换时滞奇异系统的最优保成本控制［J］.系统工程与电子技术，2011，33(6):1358-1361.Gao Z R，Ji Z C.Optimal guaranteed cost control for a class of switched singular systems with time-delay［J］.Systems Engineering and Electronics，2011，33(6):1358-1361.

［7］曾爱华，金朝永，任建功，等.持续有界扰动下一类不确定时变时滞大系统的分散鲁棒镇定［J］.广东工业大学学报，2010，27(2):71-76.Zeng A H，Jin C Y，Ren J G，et al.Decentralized robust stabilization for a class of large-scale delay-dependent systems with bounded persistent disturbances［J］.Journal of Guangdong University of Technology，2010，27(2):71-76.

［8］张冬梅，俞立.一类不确定奇异时滞系统的保性能控制［J］.浙江工业大学学报，2004，32(1):105-109.Zhang D M，Yu L.The guaranteed cost control for a class of uncertain singular time-delay systems［J］.Journal of Zhejiang Universith of Technology，2004，32(1):105-109.

［9］张志飞.具有变时滞的线性系统的时滞相关稳定性［J］.系统工程与电子技术，2001，23(2):61-70.Zhang Z F.On delay-dependent stability of lurie contol systems with stationary elements［J］.Systems Engineering and Electronics，2001，23(2):61-70.

［10］Jain S.Decentralized adaptive output feedback design for large-scale nonlinear systems［J］.IEEE Trans Auto Cont，1997，42(5):729-735.

［11］Limon D，Alamo T，Salas F，et al.Input to state stability of min-max MPC controllers for nonlinear systems with bounded uncertainties［J］.Automat，2006，42(5):797-803.

［12］刘新宇，高立群.不确定线性组合系统的分散镇定与输出跟踪［J］.信息与控制，1998，27(5)342-350.Liu X Y，Gao L Q.Decentralized robust control for linear uncertain interconnected systems［J］.Information and Control，1998，27(5)342-350.

［13］张扬.奇异系统的鲁棒控制［D］.哈尔滨:哈尔滨理工大学应用数学学院，2008.

［14］吴庆宪，王源，姜长生.区间矩阵系统低保守性鲁棒控制器的设计［J］.控制理论与应用，2000，17(2):291-295.Wu Q X，Wang Y，Jiang C S.Design of lower conservatism robust controller for interval matrix systems［J］.Control Theory and Applications，2000，17(2):291-295.

［15］桂卫华，谢永芳，吴敏，等.基于LMI的不确定性关联时滞大系统的分散鲁棒镇定［J］.自动化报，2002，28(1):155-159.Gui W H，Xie Y F，Wu M，et al.Decentralized robust control for uncertain interconnected systems with time-delay based on LMI approach［J］.Acta Automatica Sinca，2002，28(1):155-159.