谐振子偏心对半球陀螺精度的影响*

李 灿,汪立新,秦伟伟,田 颖

(第二炮兵工程大学,西安 710025)



谐振子偏心对半球陀螺精度的影响*

李 灿,汪立新*,秦伟伟,田 颖

(第二炮兵工程大学,西安 710025)

为了获得谐振子偏心对半球陀螺测量角速度的影响,首先基于谐振子径向位移动力学方程,得到了反馈激励幅值与输入角速度的关系。然后给出了谐振子偏心产生的原因,从传感器和激励器的角度分析了谐振子偏心的影响,利用等效输入角速度的思想建立了谐振子偏心的误差模型,仿真计算了谐振子偏心对陀螺测量的影响结果。最后设计实验,给出了基于二轴转台的6位置误差系数标定方法,标定结果验证了误差模型的真实性。

半球谐振陀螺;谐振子偏心;误差模型;等效输入角;误差系数标定

半球谐振陀螺具有寿命长、个体小、重量轻、功耗低、抗辐射、启动时间短以及长期稳定性好[1]等诸多优点,因此半球陀螺在卫星等空间技术领域应用广泛。然而由于国内对半球陀螺的研究起步较晚、以及国内生产工艺水平的限制,目前国内生产的半球陀螺的精度还不够。因此基于国内目前生产水平,建立陀螺的误差模型,从而提高测量精度十分重要。

目前国内对半球陀螺输出信号的研究主要集中在随机误差[2-3]、安装误差、信号处理方法[4-5]等方面。安装误差通过测量安装误差角可以补偿;随机误差可以通过Allan方差进行分离,并通过FLP滤波等方法减小误差。但是对于谐振子偏心引起的误差还没有实用模型,因此分析谐振子偏心对陀螺测量的影响对提高半球陀螺的精度意义重大。

为了获得谐振子偏心对陀螺测量的影响,本文给出了谐振子偏心的原因,从传感器和激励器的角度推导了谐振子偏心的影响,建立了谐振子偏心的误差模型,并设计了实验对相应的误差系数进行了标定。

1 谐振子径向位移动力学方程

1.1 径向位移动力学方程的建立

如图1所示,在力反馈模式下,角位置φ=0点(规定为A点)为主激励电极,激励出驻波的振型;角位置φ=45°(规定为B点)为反馈激励电极的位置,用于稳定四波腹振型,使之不发生转动。

图1 半球陀螺力反馈模式

假设A点的激磁力幅值为A,B点的激励力幅值为B,由文献[6]可知A、B两点激励力的和为

F(φ,t)=Acos(λt)cos(2φ)+Bcos(λt)×

cos[2(φ-45°)]

(1)

式中:λ为激励力的角频率。由文献[7]可知,在谐振子底端角位置φ处,其径向振动方程为:

(2)

1.2 动力学方程的求解

将径向位移w(φ,t)在X轴和Y轴上分解,得:

w(φ,t)=p(t)cos(2φ)+q(t)sin(2φ)

(3)

式中:p(t)、q(t)分别为X轴和Y轴的振幅。将式(3)代入式(2),并分别用sin(2φ)和cos(2φ)做内积,可得:

(4)

(5)

其通解为:

(6)

将式(6)代入式(4),用sin(ω0t)、cos(ω0t)分别做内积,可得c、u、d、v的值。结果为:

(7)

式中:θ为谐振子的进动角,其表达式为:

(8)

在力反馈模式下,通过调整反馈激励器的幅值可使θ=0,可得反馈激励器幅值B为:

(9)

由式(9)可以看出,陀螺测量的角速度Ω正比于反馈激励力幅值B,因此研究谐振子偏心对反馈激励的影响就能得到谐振子偏心对陀螺测量的影响。

2 谐振子偏心的影响

2.1 谐振子偏心产生的原因

当谐振子与基座、激励罩存在偏心问题时,会对输出产生影响。引起偏心的原因主要有两个:一是加工工艺、装配误差引起的偏心,这个原因引起的谐振子偏心是一个常量;二是存在垂直输入轴向线加速度aXY时,由于惯性使谐振子中心轴发生弹性形变,记偏心距分别为lxa、lya,分析可知lxa、lya是加速度a的函数。但是由于熔融石英的弹性刚度非常大,所以由弹性形变引起的偏心距非常小,在此只将lxa、lya展开为a的一次函数为:

(10)

不存在常数项的原因是常数项已经包含在lx0、ly0中。那么偏心距可表示为:

(11)

加速度引起的偏心如图2所示。

图2 加速度引起的谐振子偏心

2.2 谐振子偏心对A点激励力幅值的影响

首先分析谐振子偏心对A点传感器的影响。在谐振子与基座同心时,电容传感器极板之间的实时距离为[8-9]:

l(t)=l0-w(0,t)

(12)

式中:w(0,t)表示角位置φ=0(即A点)处的径向位移,l0为谐振子与基座同心时电容极板之间的距离。A点传感器用于测量振动幅值,从而进行反馈来稳定振幅,反馈值为谐振子振动幅度,其计算式为:

(13)

当谐振子偏心时,电容传感器极板之间的实时距离为:

l(t)=l0-w(0,t)-lx

(14)

反馈值的计算值为:

(15)

由式(13)和(15)可以看出谐振子偏心对A点传感器的反馈值无影响。

再分析谐振子偏心对A点激励力幅值的影响,由文献[10]可知:

(16)

式中:d0为激励器电极板与半球谐振子极板之间的距离。由式(7)可知,w(φ,t)的振幅为:

(17)

由式(16)和式(17)可以看出径向振幅与激励力幅值A成正比,与极板间距离的平方成反比。那么当发生偏心时,要维持振幅不变[11],则有:

(18)

解得此时需要的激励力幅值为:

(19)

2.3 谐振子偏心对B点激励力幅值的影响

谐振子偏心相当于在B点进动了角Δθ,如图3所示,可知∠BOB′=Δθ。

其计算公式为:

(20)

式中:r0为谐振子底圆面半径,即r0=OB。由式(20)可推出:

(21)

将式(19)、式(21)代入式(8),整理可得:

(22)

图3 谐振子偏心引起的进动角

在此提出等效输入角速度的概念:在真实输入角速度为Ω、谐振子存在偏心距lx、ly时,当前反馈力所对应的理想情况下输入角速度Ωeq。根据等效输入角速度的定义,将式(22)代入式(9)可得:

(23)

式中:Ωeq为等效输入角速度;Ω为真实输入角速度。这样就建立了当谐振子存在偏心距lx、ly时,测量值Ωeq与真实值Ω的换算关系。

3 谐振子偏心下的误差模型

3.1 偏心引起的陀螺漂移仿真计算

通过以上分析可以看出,谐振子偏心会对陀螺造成影响。通过仿真可以计算在输入角速度Ω=0时的误差大小。此时误差表达式为:

(24)

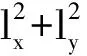
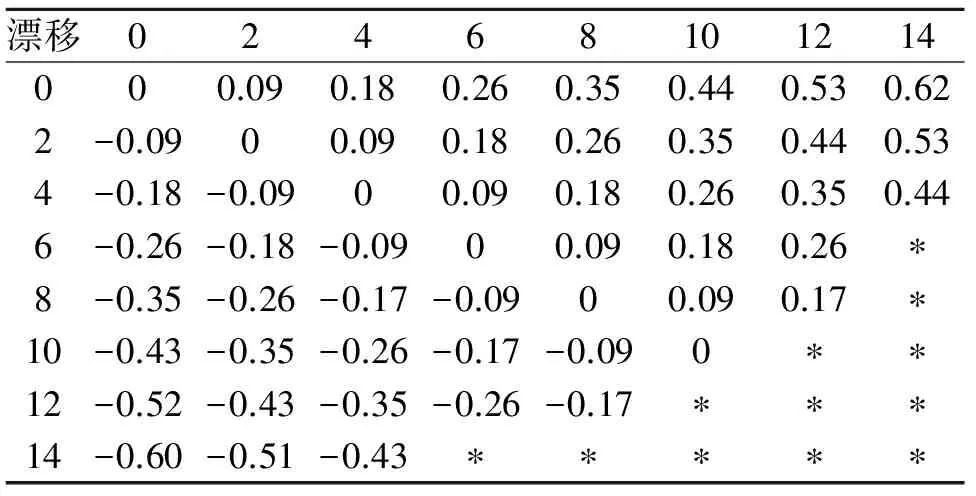
表1 误差模型的仿真结果

3.2 实验验证及补偿方法研究[12]

由于加速度会引起谐振子偏心,所以可以通过对加速度进行标定来验证误差模型(23)和模型(24)的真实有效性。经分析可知,敏感轴向的加速度对偏心距无影响,而且当陀螺应用在平台系统中时,忽略二次以上系数就可保证标定精度。因此陀螺的误差模型为:

ΔΩ=Kf+KXaX+KYaY

(25)

式中:ΔΩ表示陀螺的测量误差;Kf表示陀螺测量误差的常数项;KX、KY为相应的误差系数。

半球陀螺与传统的转子陀螺不同之处在于半球陀螺的输入轴和输出轴位于同一轴线上;而且实验条件限制,只有二轴转台可用。因此本文设计了基于二轴转台的6位置标定方法。陀螺坐标系为XYI,6位置如表2所示。

表2 对误差系数进行标定的6位置方法

考虑安装时陀螺Y轴与北向的误差角记为ϑ,规定沿逆时针方向为正;考虑陀螺的失准角影响,并事先对其标定。则

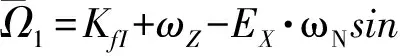
(26)

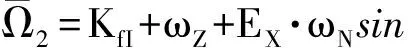
(27)

EY(-ωNcosϑ+ωZsinϑ)

(28)

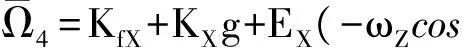
EY(-ωNcosϑ-ωZsinϑ)

(29)

EY(ωZcosϑ-ωNsinϑ)

(30)

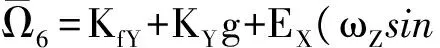
EY(ωNsinϑ-ωZcosϑ)

(31)

式中:KfI、KfX、KfY分别指I轴、X轴、Y轴垂直放置时与加速度无关的量,它们基本一致,略有差别,体现了对Kf更高精度的要求;KX、KY分别为X轴、Y轴与加速度一次项有关的误差系数;ωZ=ωiesinφ,ωN=ωiecosφ,ωie为地球自转角速度,φ为测试点纬度。EX、EY为失准角引起的误差系数。

实验处理所得到的结果如表3所示。

表3 误差系数标定结果

由标定结果可以看出,在X轴上,1个加速度引起的漂移为-5.013 8×10-4/s,那么在1个重力加速度g下陀螺漂移为-0.19 °/h,对照仿真结果可以看出,此时偏心距为4μm～6μm。在Y轴上,1个加速度引起的漂移为-8.031 8×10-6/s,那么在1个重力加速度g下陀螺漂移为-0.28 °/h,对照仿真结果可以看出,此时偏心距为8μm～10μm。实验结果充分说明了误差模型的真实有效性。

4 结论

从谐振子偏心对A、B两点激励力影响的角度出发,建立了偏心条件下真实输入值Ω与测量值Ωeq的对应关系;设计了基于二轴转台的6位置标定实验,对加速度进行标定,验证了误差模型的真实有效性;对于本次测量的陀螺,一个重力加速度在X轴上会引起4μm～6μm的偏心,在Y轴上会引起8μm～10μm的偏心,由于偏心引起的陀螺漂移大约为0.19 °/h～0.28 °/h。

[1] 李巍,任顺清,王常虹,等. 半球谐振陀螺仪谐振子品质因数不均匀引起的误差分析[J]. 航空学报,2013,34(1):121-129.

[2] 赵洪波. 半球谐振陀螺仪误差机理分析与误差抑制方法研究[D]. 哈尔滨:哈尔滨工业大学,2013.

[3] 王宇. 半球谐振陀螺铝箔技术研究与FPGA实现[D]. 哈尔滨:哈尔滨工业大学,2009.

[4] 吕志峰. 半球谐振陀螺(HRG)信号处理技术[J]. 中国惯性技术学报,2000,8(3):58-61.

[5] 江黎,周强,方针,等. 半球谐振陀螺力反馈模式下信号处理方法分析[J]. 压电与声光,2014,36(6):917-920.

[6] Zhbanov Y K. Vibration of a Hemispherical Shell Gyro Excited by an Electrostatic Field[J]. Mechanics of Solids,2008,43(3):328-332.

[7] 陈雪. 半球谐振陀螺仪的误差机理分析和实验方法的研究[D]. 哈尔滨:哈尔滨工业大学,2009.

[8] 杨道业,徐锌锋,李鹏. 双阵列式电容传感器特性研究[J]. 传感技术学报,2014,27(10):1336-1342.

[9] 熊壮,唐彬. I形MEMS谐振器的电阻差分检测方法[J]. 传感技术学报,2014,27(9):1174-1177.

[10] 祁家毅,任顺清,冯士伟,等. 半球谐振陀螺仪随机误差分析[J]. 中国惯性技术学报,2009,17(1):98-106.

[11] 赵洪波,任顺清,滕浩军. 力反馈模式振幅控制稳态模型的建立[J]. 中国惯性技术学报,2013,21(1):106-111.

[12] 谢阳光. 基于半球谐振陀螺仪的姿态测量系统研究[D]. 哈尔滨:哈尔滨工业大学,2013.

李 灿(1990-),第二炮兵工程大学控制工程系硕士研究生,主要从事惯性系统及其测试方面的研究;

汪立新(1966-),第二炮兵工程大学控制工程系教授,博士生导师。2006年获得第二炮兵工程学院导航制导与控制学科博士学位,主要研究方向为惯性技术、组合导航及微小信号测试与处理。

Influence of Resonator Eccentricity on Accuracy ofHemispherical Resonator Gyro*

LICan,WANGLixin*,QINWeiwei,TIANYing

(The Second Artillery Engineering University,Xi’an 710025,China)

In order to acquire the influence of resonator eccentricity on the accuracy of hemispherical gyro,based on the dynamic motion equation of resonator,the relationship of feedback actuator and input angular rate is established. According to the measurement principle of force re-balance model gyro,the influence of resonator eccentricity is analyzed from the view of sensor and actuator,and the error model of resonator eccentricity is calculated at the thought of equivalent input angular rate,and the result of error model is computed through simulation. Design an experiment,error coefficient calibration method is supplied through six attitudes based on biaxial turntable. The authenticity of the error model is validated by the result of calibration.

hemispherical gyroscope;resonator eccentricity;error model;equivalent input angular rate;error coefficient calibration

项目来源:半球谐振陀螺平台惯导系统技术项目(2010TC4303)

2014-12-29 修改日期:2015-03-10

C:7230

10.3969/j.issn.1004-1699.2015.06.010

V241.5;E927

A

1004-1699(2015)06-0831-05