冗余驱动电液振动台建模仿真及试验研究
, , , (大连海事大学 机械工程系, 辽宁 大连 116026)
引言
随着科学技术的发展及人们对产品可靠性要求的提高,振动模拟实验在产品生产设计及耐久性、可靠性分析等方面起到了越来越重要的作用[1]。两自由度冗余振动台是一个非线性、时变性、存在变负载、变参数的多变量复杂系统,它可以提供较大的加载力,同时也可以提高振动台的加速度均匀度,但对于冗余驱动系统,如果控制不当,就要消耗过多的能量,且各激振器之间会产生很大的内力耦合(冗余力),严重时,整个机构将无法正常运动。到目前为止,我国对振动台控制策略的研究,主要集中在伺服控制部分,而对冗余力的控制多是采用压力镇定控制方法,这是一种基于几何位置关系的方法[2],其理论推导过程尚未完善,而本研究所采用的力矩阵变换控制方法,有较详细的理论推导过程。
复杂机械系统一般包括电子控制、液压与电气驱动、机械结构等部分,这些部分集成在一起,其动力学特性极为复杂。目前还没有一款单一的软件能够精确的对此类系统进行建模与仿真分析,所以需要对系统各个部分根据各自学科的不同特点采用相应软件进行单独建模,然后把各部分的仿真模型集成到一起,运用机电液联合仿真的方法来分析它们之间的交互作用。韩寿松等运用ADAMS与AMESim对液压六自由度平台进行了仿真研究[3],马如奇等运用ADAMS与MATLAB进行了机械臂的联合仿真研究[4],王伟等运用ADAMS与MATLAB、AMESim与SimMechanics对两自由度液压振动台进行了设计。
对两自由度冗余驱动电液振动台来说,需要对系统进行详细建模,在模型的基础上研究控制算法提高系统响应。因此,本研究首先对冗余振动台系统各部分进行建模,其次,采用三状态控制与冗余力控制等控制策略对系统进行联合仿真,论文最后通过试验检验仿真模型的正确性。
1 冗余振动台系统组成及原理
两自由度冗余振动台主要由液压驱动系统与台体机械结构组成,其主要工作原理是采用可控的电液伺服阀作为电信号-液压动力转换部件来调节油压使传动装置产生周期性正弦或随机振动, 输入的电信号经过放大器控制伺服阀,伺服阀把与输入信号成比例的液压油输入液压缸,从而控制液压缸活塞带动台面及被试件运动。两自由度冗余驱动电液振动台及俯视图如图1所示。
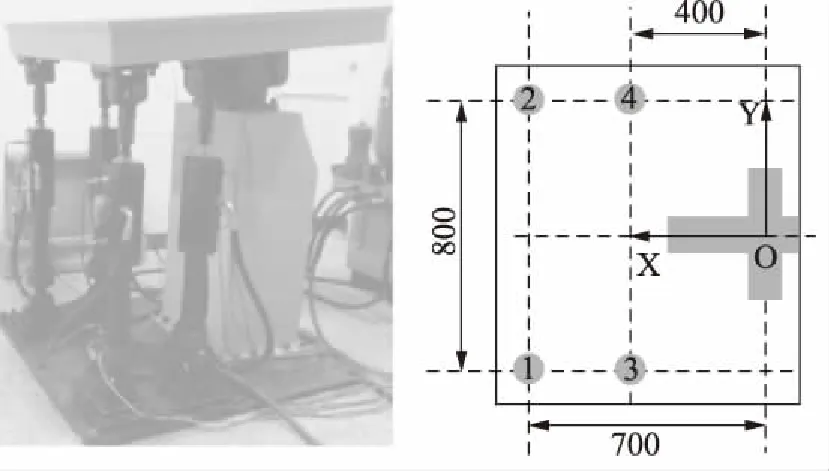
图1 两自由度冗余振动台
两自由度冗余振动台由四条液压缸驱动,可实现对振动台两个自由度的控制,四个缸①、②、③、④同时运动实现绕Y轴的转动,差动实现绕X轴的转动。
振动台伺服控制原理如图2所示。自由度合成及分解矩阵用于液压缸位移信号与台面自由度信号之间的转换。三状态控制器由三状态顺馈、三状态反馈和输入滤波器组成,用于拓展系统加速度频宽,提高系统的稳定性。力变换矩阵用于各个液压缸出力信号和冗余力信号之间的转换,实现对振动台冗余力的控制。
2 基于Simulink/SimMechanics的机械系统建模
SimMechanics是Simulink的子模块,是进行控制器和对象系统跨领域/学科的研究分析环境,它与Simulink实现无缝连接,能够提高仿真的精度与效果。在SimMechanics环境中,一般将机械部分简化成刚体、运动铰及运动副等来进行建模。如图1所示,振动台的机械部分主要由4个液压缸、上平台、大虎克铰、以及与液压缸相连的上下铰、支座和底座组成。因此,在SimMechanics对这几个部分进行建模。
2.1 液压缸结构部分模型(见图3)
激振器是推动液压振动台运动的主要结构,由活塞杆、活塞、缸筒等主要部分组成。将缸筒与活塞杆简化成刚体及它们之间的移动与转动,铰链作动器对液压缸活塞杆提供运动所需的力,传感器检测活塞杆的位移、速度、加速度。
2.2 虎克铰与底座部分模型 (见图4)
底座部分主要由与上平台连接的虎克铰、支撑上平台与虎克铰的支架、与地面相连的底座构成。
2.3 机械系统整体模型
冗余振动台机械部分主要由液压缸、上平台、大虎克铰、与液压缸相连的上下铰、支座和底座组成。将各个部分进行封装集成到一起,就建立起振动台机械系统整体模型(见图5)。

图2 冗余振动台伺服控制系统原理

图3 SimMechanics液压缸模型

图4 SimMechanics虎克铰与底座模型

图5 SimMechanics振动台模型
3 基于AMESim的液压伺服系统建模
冗余振动台的液压伺服系统主要由4组阀控对称液压缸构成给上平台提供动力,驱动上平台运动。采用AMESim工程系统建模与仿真平台对振动台液压系统进行建模。4个激振器具有相同的结构参数,伺服阀设定为理想零开口四通滑阀,供油压力不变,回油压力为零,液压缸初始位置位于中位,伺服阀阀芯也处于中位。根据振动台液压系统及相关数学模型[6],在AMESim中构建了完整的液压系统模型,设置了各元件主要参数,AMESim液压驱动系统如图6所示。
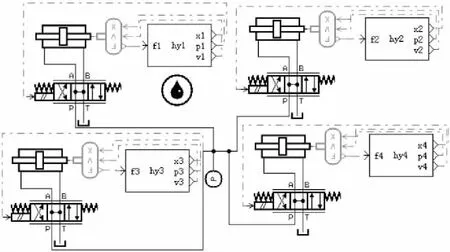
图6 AMESim振动台液压系统模型

表1 模型主要参数设置
4 基于Simulink的控制系统建模
两自由度冗余振动台由4个激振器构成冗余系统,采用自由度分解与合成矩阵,实现对振动台系统的自由度控制。由于液压伺服系统阻尼较小,故采用三状态反馈控制提高系统阻尼,改善系统的稳定性。三状态反馈控制器是在位置闭环的基础上设计的,其中加速度反馈能提高液压动力系统的阻尼比,速度反馈能提高系统固有频率;输入滤波器是通过对输入信号的二次滤波实现对振动台的加速度控制;三状态顺馈用于对消系统闭环传函中距虚轴较近的极点,拓展系统频宽[7]。采用力变换矩阵,实现对冗余力的控制。完整的控制系统模型如图7所示。
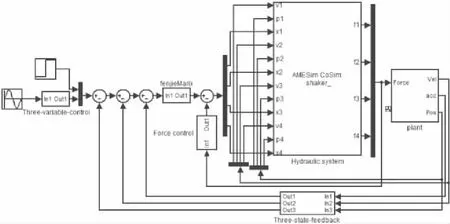
图7 Simulink控制系统模型
4.1 自由度合成及分解矩阵
振动台由两个转动自由度,4个激振器的运动范围比振动台尺寸小很多,液压缸出力方向可以看作是近似不变的。振动台在两个自由度上的实际位移定义为位移向量yc,这个是需要控制的位移,它由振动台随动参考谱给出。振动台的变形位移定义为位移向量yd,它和需要控制的激振器的出力相关[8]。定义位移向量y,它是振动台4个液压缸的实际位移。在振动台运动范围比较小的情况下,振动台实际位移和变形位移与四个液压缸的实际位移存在以下关系:
(1)
式中,C是一个4×2矩阵,D也是一个4×2矩阵。矩阵C是由四个液压缸的实际位移和振动台在两个自由度上的实际位移之间的关系决定的。
定义冗余振动台反馈信号为:Rx、Ry,液压缸的反馈信号为:Z1、Z2、Z3、Z4,按照各液压缸间的几何位置关系,有:
(2)
(3)
由上式可得自由度分解矩阵C,合成矩阵即为分解矩阵的逆。
4.2 力变换矩阵
四个液压缸激振器是从零位开始运动的,与振动台结构相比其运动范围很小,所以激振器出力方向可以近似为恒定的,振动台的变形位移是需要控制的。假设有矩阵R可以使四个液压缸的位移转换为振动台的变形位移。定义R是一个2×4矩阵,得到:
yd=Ry
(4)
然后,振动台的变形位移是由冗余力引起的,在振动台实际运动中冗余力是需要控制的。根据能量守恒定理(做功相等),可以得到:
(5)
式中:fc为振动台在两个自由度方向上的力;fd为振动台产生变形位移的冗余力;f为振动台四个液压缸的实际出力。
再由4个液压缸实际位移与变形位移及与自由度位移变换可得:
PTfc+RTfd=f
(6)
将4个液压缸的出力转换成振动台冗余力,即:
QPTfc+QRTfd=Qf
(7)
由以上公式,根据振动台运动时各个液压缸的出力,可得冗余力转换矩阵Q。至此,力变换矩阵求出,可以实现对振动台冗余力的控制[9]。
5 联合仿真与试验结果分析
AMESim与Simulink的联合仿真是通过Simulink中的S-Function实现连接的。其具体实现过程是在AMESim中经过系统编译、参数设置等生成供Simulink使用的S函数,Simulink调用这个S函数,从而实现AMESim与Simulink的联合建模与仿真[10]。
本研究建立了冗余驱动振动台系统完整的联合仿真模型,为了验证模型的正确性,在XPC环境实时控制系统下进行试验,将仿真与试验结果进行对比。
1) 系统阶跃响应
分别给振动台X自由度0.2°、Y自由度0.1°的位置阶跃信号,由图8、图9可知,模型与实际系统阶跃响应的上升时间约为0.15 s。
2) 正弦曲线跟随特性
在Simulink中分别给Rx和Ry自由度正弦加速度运动规律:
ax=400 sin(2πft),ay=200 sin(2πft),f=20 Hz。

图8 Rx自由度阶跃响应
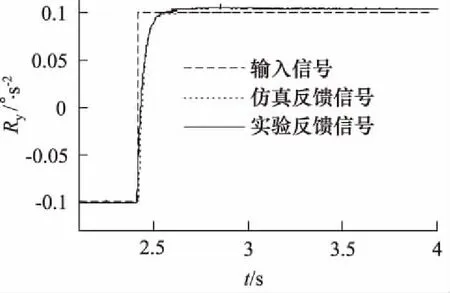
图9 Ry自由度阶跃响应
图10、图11分别是联合仿真模型与试验系统Rx、Ry自由度加速度的正弦曲线, 仿真与试验曲线相符。

图10 Rx自由度加速度响应曲线

图11 Ry自由度加速度响应曲线
由于试验环境比较复杂,受非线性等因素的影响试验曲线不够平滑,将在后期继续研究。
6 结论
首先介绍了振动台系统组成及其工作原理,给出自由度分解与合成矩阵以及力变换矩阵,然后采用Simulink/SimMechanics对机械结构部分建模,采用AMESim对液压激振系统建模,在Simulink中通过封装集成,建立系统完整的模型,实现了机电液系统的联合仿真;通过三状态控制器实现振动台的加速度控制,提高系统的加速度响应频宽,改善系统的稳定性;最后,通过与试验对比,验证了联合仿真模型的正确性。
现有的联合仿真模型中未考虑电液系统时变及非线性等因素,导致正弦曲线跟随精度不高。
参考文献:
[1]陈家焱.多点激励振动试验系统的控制策略研究[D].杭州:浙江大学,2011.
[2]郭延军.冗余振动台控制方法研究[D].哈尔滨:哈尔滨工业大学,2009.
[3]韩寿松,晁智强,刘相波.基于ADAMS和AMESim的液压六自由度平台联合仿真研究[J].机床与液压,2013,41(9): 157-159.
[4]马如奇,郝双晖,郑伟峰,等.基于MATLAB和ADAMS的机械臂联合仿真研究[J].机械设计与制造,2010,(4):93-95.
[5]王伟.两自由度液压振动台设计[D].哈尔滨:哈尔滨工业大学,2011.
[6]王春行.液压控制系统[M].北京:机械工业出版社,2011.
[7]Yang Ningning, Guan Guangfeng, Xiong Wei, et al. Acceleration Servo Controller Design for Two-axis Angle Vibration Table[J].Machine Tool & Hydraulics,2012,(24): 85-88.
[8]Weibo Liu, Guan Guangfeng, Xiong Wei, et al. Servo Design for Two Degrees of Freedom Redundant Drive Shaking Table[J]. ICMC,2014,(07):03-05.
[9]Plummer A R,Practical Multivariable Control for Multi-axis Hydraulic Servo systems[J]. Centre for Power Transmission and Motion Control,2013.
[10]张玲玲,张俊俊. 基于 AMESim 与MATLAB/Simulink联合仿真技术的接口与应用研究[J].机床与液压,2008,36(1):148-150.

