基于动网格的液压锥阀动态特性研究

　, 　, , , (解放军理工大学 野战工程学院， 江苏 南京　210007)

引言

液压锥阀以其密封性好、结构简单、响应迅速等优点在液压元件中得到了广泛的应用，特别是在压力控制和流量控制阀中，因此对于液压锥阀的研究是一个热点。但目前关于弹簧刚度对液压锥阀动态特性影响的研究较少，通常仅考虑稳态特性[1]。当前，利用流体力学相关原理对液压阀的开启过程进行分析越来越得到重视，文献[2]、[3]在给定阀芯运动速度或固定阀口开度的前提下，对流体在液压锥阀内的流动状态进行了可视化计算和研究，但液压锥阀的开启并不是一个匀速的过程，这就会造成一定的误差；文献[4]在给定入口压力的前提下，讨论了液压锥阀结构对动态性能的影响，但仅仅给出了阀芯位移随时间的变化情况。针对上述问题，基于动网格技术，以流体软件CFD-ACE+为技术平台建立了液压锥阀动态特性分析的三维数值模型，得到了弹簧刚度对锥阀开启过程动态特性的影响规律，研究结果对于液压锥阀的设计具有重要的借鉴意义。

1　三维数值模型的建立

1.1　动网格条件下的控制方程

动网格技术可以用来模拟流场形状由于边界运动而随时间改变的问题。在网格运动过程中，流场内控制体将发生改变，一般采用积分形式来表示诸守恒方程[5]：

(1)

式中，φ为通用变量，代表u、v、p等；Γ为广义扩散系数，代表μeff、μ+μt/σk、μ+μt/σε；Sφ为φ的源项；∂V为控制体积V的边界。

1.2　动网格生成方法

由于液压锥阀启闭过程中阀芯相对运动区域较小，本研究采用网格弹性变形技术生成动网格。在网格弹性变形过程中，将网格节点间的连线假想为连接节点的弹簧，初始网格的分布作为假想弹簧的平衡状态，边界网格点的位移使所有与之相连的连线产生相应的弹性应力。根据胡克定律，网格节点上的应力可表示为：

(2)

1.3　几何模型

借鉴文献[6]归纳抽象出的具有共性的液压锥阀作为研究对象，确定的结构及尺寸见图1。

图1　液压锥阀结构

该锥阀内流体的流动具有对称性，为提高计算效率，只取流动区域的一半作为研究对象，建立的用于流体力学分析的几何模型如图2所示。

1.4　网格划分

网格划分直接影响到计算精度和效率，根据研究对象的特点，采用结构网格。网格划分采用前处理软件GEOM实现，为更好地捕捉阀口处流场，对阀口区域网格进行细化。在大量试算的基础上确定了网格的数量为47222个，网格划分情况如图3所示。

图2　液压锥阀几何模型

图3　网格划分

2　边界条件与参数选取

根据液压锥阀使用的一般工况，其边界条件和参数设置如下：

入口条件：压力入口，选取6.3 MPa；

出口条件：压力出口，设为大气压；

液压油：按VG46选取，密度ρ=885 kg/m3；运动黏度μ=46 mm2/s；由于液压油压缩性很小[7]，设为不可压缩流体；

弹簧刚度：分别取100 N/mm、125 N/mm、150 N/mm、175 N/mm、200 N/mm；

湍流模型：采用k-ε湍流模型；仿真步长为10-5s。

3　液压锥阀动态特性分析

3.1　流量分析

对于液压系统来说，流量特性尤为重要，直接影响执行机构的运动情况。通过仿真，得到液压锥阀开启过程中流量的变化情况，如图4所示。

从图4看出，在锥阀开启过程中流量会有一定的波动，并且随着弹簧刚度的增加波动幅度相应减小。流量的不稳定会导致执行机构在锥阀开启过程中的速度增加或减小，从而影响到液压系统的性能。

图4　阀芯开启过程流量变化

实际工作中，液压锥阀稳态流量通常采用理论公式进行计算[4]：

(3)

将计算得到的理论值与仿真值进行比较，得到表1。

由表1可以看出，两者变化趋势一致，均是随弹簧刚度的增加而减小；仿真计算结果与理论值存在误差，这是由于理论计算所采用的流量系数一般通过经验得到，并不十分准确；同时，仿真计算结果与理论值误差较小，这也证实了仿真的可靠性。

3.2　液动力分析

在入口压力一定的前提下，弹簧刚度不同会使得阀口开度不同，导致阀芯所受的液动力不同，液动力反过来又会影响到阀芯的位移， 所以液动力和阀芯运动过程是相互影响的。在溢流阀中，稳态液动力的存在也会增大锥阀的调压偏差[8]。因此有必要对阀芯移动完毕的稳态液动力和阀芯运动过程的瞬态液动力进行研究。

1) 稳态液动力

稳态液动力是指阀芯移动到平衡位置时，流体因动量改变而附加作用在阀芯上的力。稳态液动力的理论计算公式为[8]：

F′=-ρQv1cosα

(4)

通过仿真得到的稳态液动力Fw=F-F0。其中，F为液压锥阀阀芯所受总力，F0为仿真得到的阀口静压力(F0=356 N)。仿真得到的稳态液动力与理论值如表2所示。

由表2可知，随着弹簧刚度的增加，阀芯受到的总流体力增加，这会增加阀芯所受的应力；稳态液动力均为负值，表明液动力的方向使得阀芯趋于闭合，利于阀芯的稳定；随着弹簧刚度的增加，阀芯受的稳态液动力的绝对值变小，这是由于虽然随着弹簧刚度增加导致液流在阀后的流速增加，但是液压锥阀流量相应减小。从表2还可看出，仿真值与理论值存在一定误差，但在可以接受的范围内，这是由于在公式计算中使用半锥角代替节流口处的液流角，但是实际的液流角并不等于阀芯的锥角，同时理论计算并没有考虑到锥阀内部结构不同以及流场微观流动情况带来的影响。

2) 瞬态液动力

瞬态液动力是阀芯在移动过程中(即开口大小发生变化时) 阀腔内液流因加速或减速而作用在阀芯上的力。将阀芯在不同瞬时所受的总力减去稳态时阀芯表面所受的力即可得到不同弹簧刚度下阀芯的瞬态液动力，变化情况如图5所示。

表1　稳态流量理论值与仿真结果

表2　稳态液动力理论值与仿真值对比

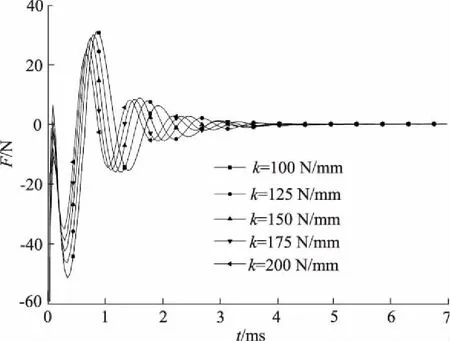
图5　阀芯受瞬态液动力

从图5可以看出：① 锥阀瞬态液动力存在波动，峰值随着弹簧刚度的增加而减小；② 随着弹簧刚度的增加，瞬态液动力减小到零所需的时间也逐渐缩短； ③ 瞬态液动力为负值表示其力方向与阀芯运动方向相反，起到正阻尼作用，利于锥阀的稳定，反之则对阀芯起到不稳定作用。

3.3　阀芯运动情况分析

阀芯的运动情况是由阀口压力、液动力以及弹簧力共同决定的，不同弹簧刚度下仿真得到的阀芯瞬态位移、速度以及加速度变化情况分别如图6所示。

从图6中位移变化情况可以看出，随着弹簧刚度的增加，阀芯稳态位移减小，并且当弹簧刚度较大时，位移减小不明显，即阀芯的稳态位移与弹簧刚度不成线性关系，这是由不同弹簧刚度下锥阀所受液动力不同而引起的；阀芯位移超调量随着刚度的增加而减小。

从图6中速度变化情况可以看出，随着弹簧刚度的增加，阀芯运动速度的峰值减小，并且更快地达到平衡位置，阀芯速度的波动也会影响到内部流场的流动状态。

从图6中加速度变化情况可以看出，不同弹簧刚度下加速度数值均较大且峰值随着弹簧刚度增加而减小；随着弹簧刚度的增加，加速度趋于零所需时间变短；在整个过程中，加速度的值都存在小范围内的波动，这是由于液流不稳定造成冲击引起的。

4　结论

通过对液压锥阀开启过程的仿真分析，得到了弹簧刚度对液压锥阀动态特性的影响规律， 可以为提高液压锥阀的动态性能和结构优化提供依据。主要结论包括：

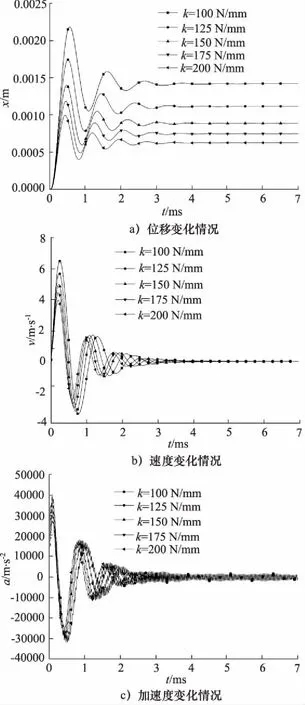
图6　不同弹簧刚度下阀芯动态响应

(1) 在压力一定的条件下，随着弹簧刚度的增加，锥阀稳态流量、瞬态流量波动幅度均减小。

(2) 随着弹簧刚度的增加，阀芯受到的总力增大；但是，稳态液动力的绝对值、瞬态液动力的波动幅值均减小；阀芯受总力的增大会减小液压锥阀的使用寿命，而稳态液动力的减小可降低调压偏差，瞬态液动力波动幅值的减小可以改善阀芯瞬时的受力情况。

(3) 随着弹簧刚度的增加，阀芯的稳态位移减小；阀芯运动的位移、速度和加速度波动幅值均减小，并且更快地达到稳定位置，利于减小冲击和振动。

参考文献：

[1]朱海燕,曹文琴,向毅.铝合金液压阀岛中溢流阀结构设计和静态特性计算[J].机床与液压,2012,(21):123-126.

[2]郑淑娟,权龙,陈青.阀芯运动过程液压锥阀流场的CFD计算与分析[J].农业机械学报,2007,(1):168-172.

[3]李辉,柯坚,刘晓红.基于CFD的液压锥阀结构特性分析[J].流体机械,2009,9(37):33-36.

[4]李惟祥,刘晓红,邓斌.基于CFD的液压锥阀动态和静态性能研究[J].液压气动与密封,2011,(6):25-28.

[5]何晓晖,孙宏才,程健生,等.基于动网格的液压阀阀芯启闭中的液动力分析[J].解放军理工大学学报(自然科学版),2011,(5):491-495.

[6]郑宁舟.锥阀流动仿真分析及其结构改进[D].西安:长安大学,2011.

[7]Zhi-fei Peng,Chun-geng Sun,Rui-Bo Yuan,Peng Zhang.The CFD Analysis of Main Valve Flow Field and Structural Optimization for Double-nozzle Apper Servo Valve.Procedia Engineering[J].2012,31(1):115-121.

[8]刘桓龙,洪威,王国志,等.锥阀芯稳态液动力补偿研究[J].机床与液压,2013,19(41):22-24,28.