一条“引线”让数学课堂升温

胡志斌

[摘 要] 一条引线，可能是一个知识点，也可能是一个关键词等等，我们不要小瞧它，它价值连城，是我们了解知识整体的一个引子，一个催化剂. 教师要拟出一条引线作为通向数学知识学习领地的船只，悠悠小船必定摆渡更多的学生，学生对知识的呼唤也定能让课堂升温.

[关键词] 课堂教学；引线；触类旁通中国的数学教师通常怀着“只讲教学大纲上的内容”的思想来教学，这大部分原因是由于应试教育的弊病造成的. 教师秉灯夜读，根据教学大纲，写教案，拟定教学目的、教学内容、教学重点及难点. 对教学大纲的迷信，使教师教学拘泥在一个狭窄的知识领域里，课堂失去张力和弹性，变得枯燥无味. 换句话说，教师只看到摆在面前的知识，而无视由知识做引显现的东西. 长此以往，学生的解题思维避免不了会有局限性，而且没有一条知识引线贯穿的知识群是很容易散失的，不成系统的知识也难免不会被学生遗忘. 所以教师要设定一条引线，用一个知识点做引子，引出无数休戚相关的知识点，并紧密聚集，形成庞大的知识群，继而让学生深刻记忆，充满兴趣地投入到数学课堂的温度中.

从无到有，万物伊始自有它的源头，这一源头就像大树的根基，向以根基为据点伸展出来的每一个枝条输送养分，这样万事万物才能得以兴旺隆泰. 而无根或者根死，客观世界的物也就随之凋零、消亡. 所以根很重要，它是事物产生发展的条件，从这一渊源处，我们又会重新认识所发展的事物的性质，从而看到像老子在《道德经》中提到的那样：“一生二，二生三，三生万物”，世界在我们眼前不是单一的一条路径，而是繁复交叉. 对于知识来说也是如此，一知识点的产生也自有它的渊源，对渊源的追溯会使知识本身更加深邃丰富，而且当我们了解其源头，也相应地了解知识本身的存在状态，它不再是一个学生难以逾越的谜，而是一场有趣的探索之旅. 对于教师要利用学生那种追本溯源的情结，找一根引线，将学生很自然地引进知识的源头处，汲取知识的真实口吻. 这不但增强知识的丰富性，还拓宽了学生的视野，培养了学生的发散思维. 此外，还使学生看到了一个丰富多彩的数学城堡，他们兴趣十足走入其中，进行一场魔幻之旅.

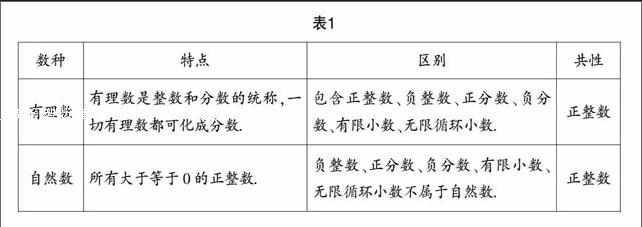
初中数学教材中涉及“数”，数是人类社会最习以为常的元素，因为它频繁出现在生活中，人们习惯了它的如影随形，将其看做最平凡不过的知识点去对待，进而忽视了它的丰富性. 受升学压力“戕害”的教师也是如此，数的常用性使其忽略了数的可探究性，课堂教学没有个性，人云亦云，甚至变成思维的囹圄，斩断知识外延性的东西，管窥蠡测，毫无张力，画知识为牢. 尤其是教师屏蔽了知识本源的东西，知识无根而起，学生难免陷入学习的僵局. 所以，广大教师更应该在实践中进行总结，摒弃教学上的不足，全面地看待知识，寻觅一条引线，探究知识产生的渊源，为学生对教材知识的学习挖地基，使其牢固记忆. 我们且以有理数这一知识点展开说明. 有理数是数的一个类别形式，虽然在数以万计与数有关的概念中有理数只是冰山一角，但它是人们认知范畴扩大的一个象征. 人能够认知有理数的存在也是有一定的机缘的，它作为“数”的一个子集，必然趋于数的方向. 所以教师可以以大的集合——“数”作为引线，探求有理数产生的渊源. 人类的祖先开始以群居为主，他们不断地发挥主观能动性来维持长期的生活. 于是有了语言，有了“有”和“无”这两个关于数的朦胧概念. 后来，人类开始进行部落分化，“有”又被肢解成四部分“一”、“二”、“三”、“多”. 在生活方式渐趋完善的过程中，数又分解成自然数、实数、整数、负数、有理数等等.

数学知识也是有“祖籍”的. 在课堂教学中拿出教材里单章的知识点，我们可能会认为那就是个体的知识，是与外界毫无联系，单独存在一个空间里的知识，但若是将这一空间的阻断破除开，你会发现仍会有许多知识同其联系，同属一种血统，完全可以被归纳成一个知识群，“认祖归宗”. 但更多的教师似乎忽略知识这种承上启下或平行产生的联系性，只是注重学生对指定的知识点的记忆情况和解题效率. 这样一来，学生知识储备比较分散，不能形成完整的知识系统，解题和记忆失去灵活性，容易陷入遗忘的境地. 所以，教师要以一求十，建立知识“共荣圈”，让学生获得学习的乐趣，且在进行解题或知识点记忆的时候，可以窥一斑而见全身，以一个知识点引出与之相关的一类知识点，从而以百分之十的力气争取百分之九十的收获. 而在这之前，教师要找到一条可使知识点结群的引子，也就是得以继续寻找其他知识点踪迹的路眼. 可以是一个知识点，可以是笼统的一个概念等等.

事物间的联系分两种情况，一种可能是此事物本身与彼事物本身存在某种客观而不以人的意志为转移的共通性；一种可能是此事物与彼事物间人为所建立的互通桥梁. 可以说联系使客观事物紧密起来，世界成为一张密度紧凑的网. 关于数学知识点也是这样，由一个知识点当做探究的起点，我们可能会找到客观存在着的与之联系的其他知识，或者是运用我们的逻辑人为地为知识拉绳牵线. 还以有理数这一知识点为例. 有理数是数肢解出来的一个分支，由这一分支做引线，我们还可以联系到数的其他分支，比如实数、整数、小数、分数、百分数、正数、负数、自然数等等. 教师可以根据这一点对学生进行提问：“我们现在所学的是有理数，它属于数的一个分支，那么通过预习，还有对以前知识的回忆，你能说出除有理数之外的其他分支吗？”学生纷纷举手，一一列举. 然后教师要引导学生进行一次人为的联系，通过列表进行对比区别找出这些数的共通之处. 如表1.

俗话说：“好记性不如烂笔头”，反复的写或演练可能会使人加强记忆. 但永不遗忘只有很小的几率. 对于数学知识更是如此. 由于数学知识的抽象性，我们要并用形象思维和逻辑思维，这些仍不够，在错综的知识结构中，我们还要建立联系，运用其他知识来解这一知识，用这一知识来说明另一知识. 这就涉及一个行之有效的方法. 方法不对，或者不灵活都会致使记忆无效. 所以仅凭笔头下的功夫进行死记硬背，是不能有效的学习数学，记忆知识的. 到这里，大家会发生疑问，那该如何去记忆？我们要找到一条引线，且保证这条引线贯穿所记忆的全部知识. 就是将知识散落的骨架整理起来，形成一个整体，我们顺着整体来记忆个体部位. 个体部位的位置、特点了解之后，对整体的记忆也就明朗起来了.

例如中心对称、轴对称、中心对称图形、轴对称图形，这四个知识点我们常常会互相混淆，如何正确永久记忆成为教师最为头疼的事情. 而为了记下这四个知识，有学生居然熬夜到凌晨，学习效率可想而知了. 而找引线，是把知识点串联，在串联的过程中，区别联系一目了然，记忆也变得方便简洁. “对称”是这四个知识点串联起来的一条引线. 轴对称是关于两个全等图形之间的位置关系，而轴对称图形是关于一个图形对折之后，直线两旁互相重合的两部分. 把轴对称的两个图形看做一个图形，这个图形是轴对称图形，把一个轴对称图形中的对称部分看成两个图形，它们是轴对称. 根据对称这条引线，我们可以看到轴对称是两个图形间的关系，而对称图形是关于一个图形对折之后的对称. 中心对称及中心对称图形也是如此，根据对称这条引线，找它们的对称点. 区别对称点，便将这些知识区别开来了.

总结

一条引线，可能是一个知识点，也可能是一个关键词等等，我们不要小瞧它，它价值连城，是我们了解知识整体的一个引子，一个催化剂. 它有利于我们在学习数学的过程中了解知识演化的渊源，举一反三，建立知识间联系，巩固记忆，提高学习的效率.