道是无圆却有圆
[摘 要] 让学生学得轻松,作为教师,就要讲究策略. 若能告诉学生一类问题的解法通则,则是解题教学的一种策略. 本文以几何证明题中添辅助图为例,加以阐述.
[关键词] 辅助圆;构造法;三角形;线段如何减轻学生过重学业负担,促使学生全面发展是摆在学科教师面前的一个重要话题. 要让学生学得轻松,作为教师就要讲究教学策略,使学生在课堂上易懂、易学,从而爱学、乐学,这在解题教学中更显重要. 若能告诉学生一类问题的解法通则,就是解题教学的一种策略. 下面以几何证明题中添辅助圆为例,加以阐述.
初中数学中有些问题看似与圆无关,但如果我们根据题目中的已知条件构造辅助圆,再利用圆的有关性质来解决问题,往往能起到化隐为显、化难为易、化繁为简的解题效果. 那么,何时构造合适的“辅助圆”,使得解题举重若轻,柳暗花明呢?
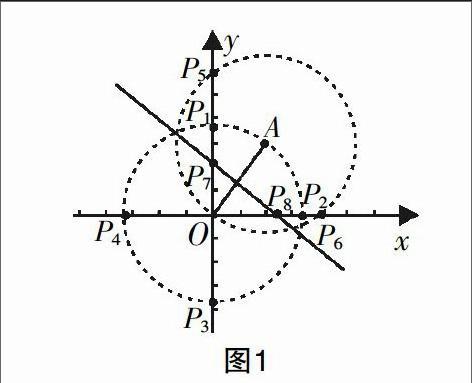
例1 (2013昆明)在平面直角坐标系xOy中,已知点A(2,3),在坐标轴上找一点P,使得△AOP是等腰三角形,则这样的点P共有________个.
解析:如图1,在平面直角坐标系中,因为O,A两点固定不动,相当于已知等腰三角形一边OA,OA既可作底,又可作腰,因为等腰三角形中有两边相等,所以我们可以利用同圆中半径相等这一性质,通过构造圆来解决.此题应分三种情况考虑:
①当OA为腰、∠AOP为顶角时,可以以点O为圆心、OA为半径作圆,交y轴于P1,P3点, 交x轴于P2,P4点;
②当OA为腰、∠OAP为顶角时,可以以点A为圆心、OA为半径作圆,交y轴于P5点,交x轴于P6点;
③当OA为底时,作OA的中垂线交y轴于P7点,交x轴于P8点;
综上,符合条件的点P共有8个.
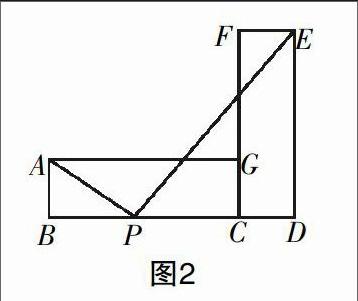
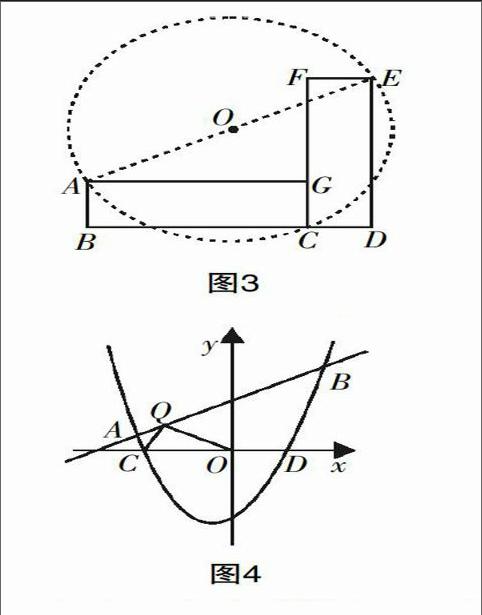
例2 (2006陕西)如图2,矩形ABCG(AB A. 0 B. 1 C. 2 D. 3 解析:要使∠APE=90°,则可以构造以AE为直径的圆,根据“直径所对的圆周角是直角”,如果此圆与线段BD有几个交点,则使∠APE为直角的点P的个数就有几个,通过作图(如图3所示)可知,以AE为直径的圆O与BD有两个交点,所以使∠APE为直角的点P的个数是2. 例3 (2014南宁)如图4,在平面直角坐标系中,抛物线y=x2+(k-1)x-k与直线y=kx+1交于A,B两点,点A在点B的左侧. 抛物线y=x2+(k-1)x-k(k>0)与x轴交于点C,D两点(点C在点D的左侧),在直线y=kx+1上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时k的值;若不存在,请说明理由. 解析:本题有多种解法,但若能领悟到“存在唯一一点Q,使得∠OQC=90°”的含义即以OC为直径的圆与直线AB相切于点Q,从而构造“辅助圆”,不失为一种好的解题方法. 例4 (2008济宁)如图6,四边形ABCD中,AB=AC=AD,若∠CAD=76°,则∠CBD=____度. 解析:根据圆的定义:到定点距离等于定长的点的集合. 本题中已知AB=AC=AD,即点B,C,D到点A的距离相等,容易想到构造以A为圆心,AB为半径的圆(如图7),则B,C,D都在☉A上,所以∠CAD是弧CD所对的圆心角,∠CBD是弧CD所对的圆周角,所以∠CBD=∠CAD=38°. 例5 如图8,在四边形ABCD中,AD∥BC,AB=AC=AD=2.5,CD=3,求BD的长. 解析:由条件AB=AC=AD=2.5,想到构造以A为圆心,AB为半径的圆,则点C,D均在☉A上(如图9),延长DA交☉A于点E,连结BE,由AD∥BC可以推得BE=CD=3,在Rt△BDE中,BE=3, DE=5,由勾股定理可得BD=4. 例6 (2014陕西)(1)如图10,在△ABC中,∠ABC=60°,BC=12,AD是BC边上的高,E,F分别为边AB,AC的中点.当AD=6时,BC边上存在一点Q,使得∠EQF=90°,求此时BQ的长; (2)有一山庄,它的平面图为如图11所示的五边形ABCDE,山庄保卫人员想在线段CD上选一点M安监控装置,用来监视边AB.现只要使∠AMB约为60°,就可以让监控装置的效果达到最佳.已知∠A=∠E=∠D=90°,AB=270 m,AE=400 m,ED=285 m,CD=340 m. 问在线段CD上是否存在点M,使∠AMB=60°?若存在,请求出符合条件的DM的长;若不存在,请说明理由.
解析:(1)由条件“当AD=6时,BC边上存在一点Q,使∠EQF=90°”,动点Q对定线段EF所张的角为直角,由“直径所对的圆周角是直角”想到构造以EF为直径的☉O.
如图12,以EF为直径作☉O,过点O作OQ⊥BC,垂足为Q,连结EQ,FQ,易证OQ=OE=3,从而☉O与BC相切,符合条件的点Q唯一,再过点E作EG⊥BC,垂足为G. 所以EG=3,所以四边形OEGQ是正方形.
在Rt△EBG中,∠B=60°,EG=3, 所以BG=,所以BQ=GQ+BG=3+.
(2)要满足动点M对定线段AB所张的角∠AMB=60°,由此联想到“一条弧所对的圆周角等于它所对的圆心角的一半”,于是先构造以AB为底边,顶角为120°的等腰三角形OAB,再以点O为圆心,AB为半径作圆O,若该圆与线段CD有交点M,则∠AMB=60°.
如图13,先判断☉O与直线CD的位置关系,作OH⊥CD于点O,OP⊥AB于点P, 则AP=AB=135. 在Rt△OAP中,∠OAP=30°,则☉O的半径OA=90,OH=DE-AP=150<90,所以☉O与直线CD相交,现要考查☉O与线段CD是否有交点,且交点有几个.设☉O与直线CD的交点为M,则在若点M在点H的左边,则DM=DH+HM=400-45+30>CD,此时点M不在线段CD上,
综上所述,在线段CD上存在唯一的点M,使∠AMB=60°,此时DM的长为(400-45-30)米.
例7 (2013呼和浩特)在平面直角坐标系中,已知点A(4,0),B(-6,0),点C是y轴上的一个动点,当∠BCA=45°时,点C的坐标为__________.
解析:要满足动点C对定线段AB所张的角∠ACB=45°,根据“一条弧所对的圆周角等于它所对的圆心角的一半”,想到构造以AB为斜边的等腰直角三角形PAB,以P为圆心,PA为圆心作☉P,则该圆与y轴的交点就是满足条件的点.
本题根据点C的位置可分两种情况:
综上,细心观察题目所给出的条件及所要解决的问题,若能与圆结缘,构造一个辅助圆,以它为载体,去重新认识题中所给出的角、线段、三角形等基本图形,再结合圆的一些特有性质,去分析和探讨问题,往往能使我们柳暗花明,豁然开朗. 当然,能构造“辅助圆”情况远远不止文中所给出的三种,只要我们多观察,多思考,多探究,数学解题就会变得充满活力和乐趣,使学生爱学,乐学数学,从而使得“减负提质”真正落到实处.

