基于特征融合的指节折痕识别算法研究*

徐　娟，罗荣芳（.广东环境保护工程职业学院机电工程系，广东佛山　586；.广东工业大学物理与光电工程学院，广东广州　50006）

基于特征融合的指节折痕识别算法研究*

徐娟1，罗荣芳2
（1.广东环境保护工程职业学院机电工程系，广东佛山528216；2.广东工业大学物理与光电工程学院，广东广州510006）

摘要：手指指节折痕同指纹和掌纹一样，具有唯一性、稳定性及可区分性的特点，可作为一种用于人体身份识别的生物特征。针对手指指节折痕的分布特征和形状特征，研究一种基于特征融合的指节折痕识别算法。首先利用Radon变换对指节折痕子图像进行变换，形成投影矩阵；其次利用奇异值分解方法对投影矩阵进行奇异值分解，从而形成指节折痕特征矢量；更进一步，考虑指节折痕特征比较简单的特点，重点研究了指节折痕的特征融合策略，用以描述指节折痕特征以达到最大的可区分性；此外定义了一种城区距离来衡量不同指节折痕特征之间的相似度，进行指节折痕特征匹配。最后在自建图像数据库中进行了测试，验证了算法的可行性及有效性。

关键词：生物特征识别；指节折痕；Radon变换；奇异值分解；特征融合策略；城区距离

*国家自然科学基金资助项目（编号：61305069）

0　引言

随着网络与通信技术的飞速发展，信息安全已成为一个日益受到重视的问题。保证系统安全的必要前提是身份鉴定，证件、各种卡、密码等传统的身份识别方法由于其自身固有的缺陷及不足已难以满足安全需求，近年来迅速发展的生物特征识别技术，即利用人体固有的生理特征或行为特征来进行个人身份鉴定的技术，则为个人身份鉴定提供了一种更为安全可靠、使用更方便的技术，在国家安全、司法、电子政务、金融、电子商务等领域具有广阔的应用前景[1-3]。当前这方面的研究主要集中在指纹识别、语音识别、掌纹识别、人脸识别和虹膜识别等。但任何一种生物个体用作生物识别时，根据使用者接受的友好程度、成本费用和系统性能等，都有其优点和不足之处，其选择依赖于实际的应用场合，不可能期望任何一种单一的生物特征满足所有的实际需要，因此，发展新的人体生物特征识别技术仍然是一项重要的任务。

同指纹和掌纹一样，手指指节折痕具有唯一性、稳定性及可区分性的特点，完全可以用来确定一个人的身份，即可作为一种用于人体身份识别的生物特征，因此基于指节折痕的生物特征识别方法研究也受到了更多的重视，并取得了一定的研究成果[2-4]。在人体手指内侧的指节表面分布一些比指纹特征更显著的特征，称之为指节折痕，是鉴别身份的又一重要的生理特征，它相对其他生物特征具有识别快捷、对噪声不敏感、存储量小和设备费用较低等特点。有效地提取稳定而又具有区别特性的指节折痕特征是实现指节折痕识别的一个关键。指节折痕对不同的个人是相异的，不同个人的指节折痕形状、长度和走向都是不相同的，这些都是借以将指节折痕作为生物特征的一个重要原因。文献[4]将指节折痕图像只朝一个方向做投影，会部分丢失各指节折痕线的形状和空间位置信息。为了弥补这种缺陷，提出了基于Radon变换和奇异值分解的特征提取策略。

仔细观测指节折痕线，大部分折痕线是分布在几个不同的方向，而Radon变换可以以不同的方向投影来表征图像，可以满足提取指节折痕特征的需要。因此，利用Radon变换将二维ROI （Region of Interest，即感兴趣区域）图像沿几个不同的方向投影到一维空间，既可以使运算量减少，又能有效地表征折痕特征。然后在用不同角度下的投影数据构成的投影矩阵的基础上，利用奇异值分解方法对其进行奇异值分解，从而得到指节折痕特征矢量。由于折痕特征简单，需进一步探讨采用合适的特征融合策略来描述手指指节折痕特征以达到最大的可区分性。最后利用城区距离来衡量不同类别间的相似度，在自建的数据库上进行匹配识别试验。

1　Radon变换和投影矩阵

Radon变换原理最早是奥地利数学家J.Radon提出的。Radon变换是层析(Computed Tomogra⁃phy，CT)技术或重构问题(Reconstruction problem)等的数学理论基础。目前，Radon变换已在图像分析、信号重构和模式识别等方面获得广泛的应用[5-11]。

Radon变换是计算图像在某一特定角度平行射线方向上投影的变换方法。图像的Radon变换反映了图像在不同射线方向上的投影特征。二维函数f(x，y)的Radon变换的定义如下[6]：

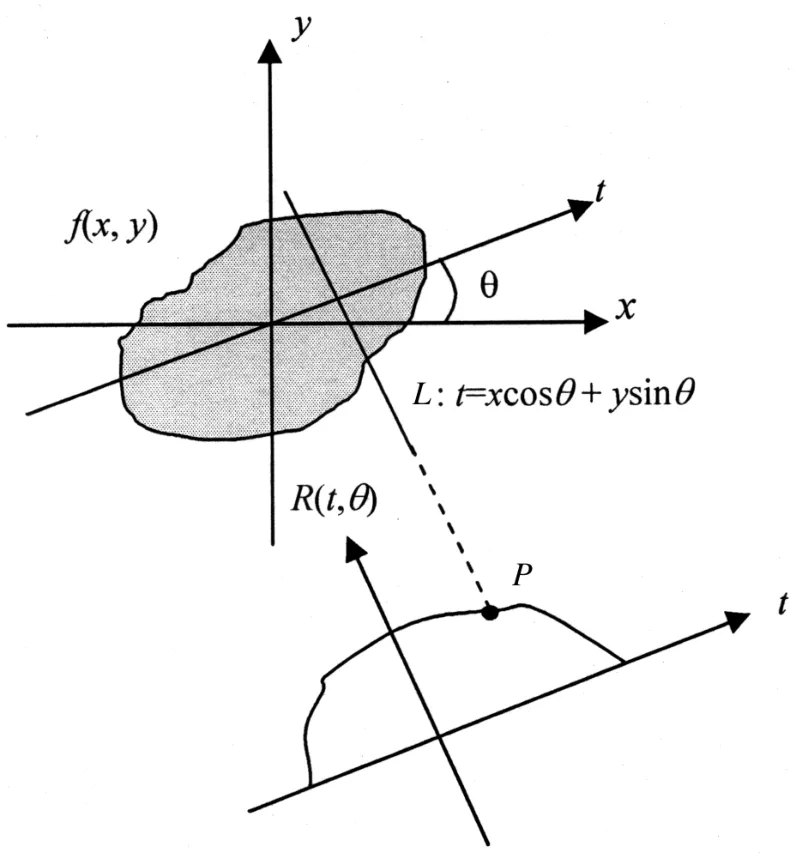
图1　f(x，y)的Radon变换

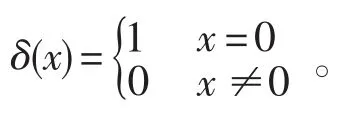
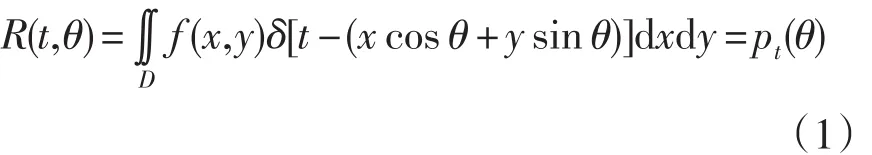
t代表着直线L离坐标原点的的距离，表示为t=xcosθ+ysinθ。这里为了说明和计算的方便，一般采取规范化的表示式，即：-1≤t≤1，0≤θ≤2 π。

下面讨论投影矩阵的构成。

由Radon变换的定义可知，沿某一个角度对ROI图像进行投影时，得到的是图像在这个方向的一个一维序列。将θ ϵ[0，π]角度范围等分为n个投影角度{θ0,θ1,…,θn-1}，在每个角度处的投影点个数为m，若对角度θi进行投影，则可得到m个投影值R(tj，θi) (i=0，1，…，n-1；j=0，1，…，m-1)。由全部角度投影结果组成的矩阵称之为投影矩阵A：

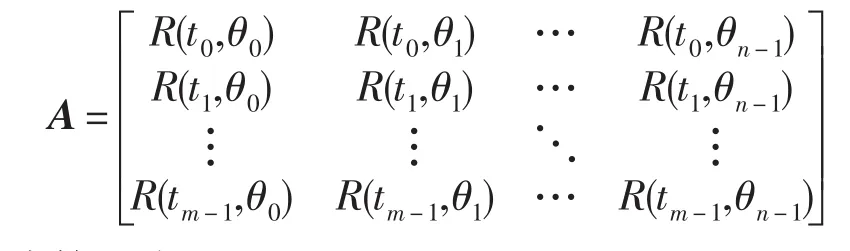
或简写为：

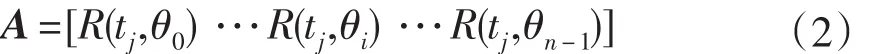
其中每一列表示某一个角度下图像f(x，y)的投影序列。

2　异值分解（SVD）和特征矢量的构成

奇异值分解(singular value decomposition，简称SVD)是一种有效的代数特征提取方法。自从GouBle和Reinsl在1970年提出了计算矩阵奇异值分解的算法以来，奇异值分解就首先成为求解最小二乘问题(Least Square Problems)的一种有效工具，已经在图像数据压缩、图像处理、模式识别和信息隐藏中得到了广泛应用[11- 15]。

定理1设m×n矩阵A是一个秩为r的实数矩阵，则存在两个正交矩阵（即UTU=I和VTV=I，I为单位矩阵）U=(u1，……，um)ϵRm×m与V=(v1，…，vn)ϵRn×n，以及对角矩阵∑=diag（λ1，λ2…，λr，0，…，0）ϵ Rn×n，r=min(m，n)，使得：

其中，λi(i=1，…，r)为矩阵A的奇异值，即(i=1，…，r)是矩阵AAT与ATA的非零特征值；ui与vi分别是AAT与ATA对应于λi的正交归一化特征向量。

定理2设AϵRn×n，矩阵A的奇异值为λ1，λ2…，λr，λr+1，λr+2，…，且λ1≥λ2≥…≥λr>λr+1=λr+2=…=0，ui，vi（i=1，2，…，r)分别为AAT与ATA对应于非零特征值λi的特征向量，则rank(A)=r，

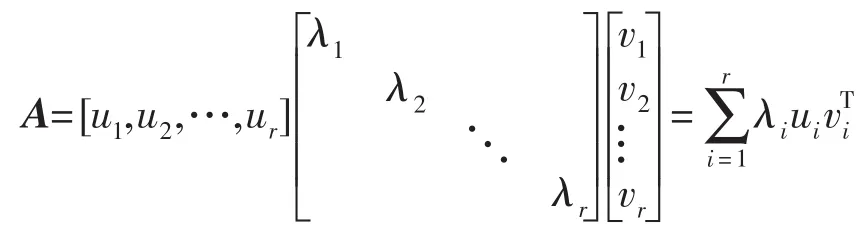
由于U和V是正交矩阵，所以对角矩阵可以用下式求解：

将矩阵所有奇异值按从大到小排列所得到的向量[λ1,λ2,…,λr,0,…,0]T即为矩阵的奇异值特征向量。当所有的奇异值按从大到小排列时，奇异值对角矩阵S是唯一的，该矩阵的奇异值特征向量也是唯一的，即奇异值由矩阵A唯一确定，于是奇异值特征可以作为描述灰度矩阵的一种数值特征。

同理将奇异值分解理论应用到投影矩阵（见式（2）），用式（4）计算出它的奇异值，则由奇异值按从大到小排列所得到的特征向量表征了矩阵A的本质特征。通过一定规则的奇异值特征向量的降维（一般的做法是保留矩阵的较大奇异值，忽略较小奇异值），可以将大多数与分类有关的折痕信息压缩到相对小的特征空间，进而形成表征指节折痕特征的特征矢量。

3　特征矢量的组合策略

由于折痕特征简单，需采用合适的特征融合策略来描述手指指节折痕特征以达到最大的可区分性。本文提出的特征矢量融合的算法过程如下。

（1）对手指指节折痕图像施以Radon变换得到一系列的投影数据，将其组合在一起后构成一投影矩阵。从整个手指指节折痕图像通过变换所求出的投影矩阵，代表的主要是全局信息，其描述局部信息的能力是有限的。为了刻画指节折痕的局部信息，在运用Radon变换之前，先将ROI图像等分为两部分：ROI1和ROI2。第一部分只包含第一指节的折痕，第二部分则只含有第二指节的折痕。这样可以得到代表整个手指指节折痕的投影矩阵A、代表第一指节折痕特征的投影矩阵A1和代表第二指节折痕特征的投影矩阵A2。

（2）运用式（4）求出上述三个投影矩阵的奇异值，并将奇异值按从大到小排列形成一奇异值特征矢量，而指节折痕特征矢量则由其最大的前K个奇异值构成，即使这里a=0.99。

（3）将三部分特征矢量经过加权组合构成描述手指指节折痕特征的特征矢量FV，即：

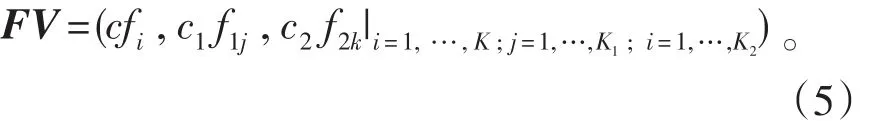
其中，fi=log10λi，f1j=log10λ1j，f2i=log10λ2k，λi,λ1j,λ2k分别表示整体部分投影矩阵A的奇异值、第一部分投影矩阵A1的奇异值和第二部分投影矩阵A2的奇异值；c、c1和c2分别为权系数，一般有，c、c1和c2，具体大小由实验确定。

整个基于特征融合的指节折痕特征提取的过程描绘于图2。

4　指节折痕特征的匹配

由前面的分析研究可知，指节折痕特征矢量是由三部分特征矢量组合而成的，即由整体部分与两个局部部分特征矢量组成。定义如下的城区距离(City Block Distance)来衡量不同手指指节折痕特征之间的相似度：

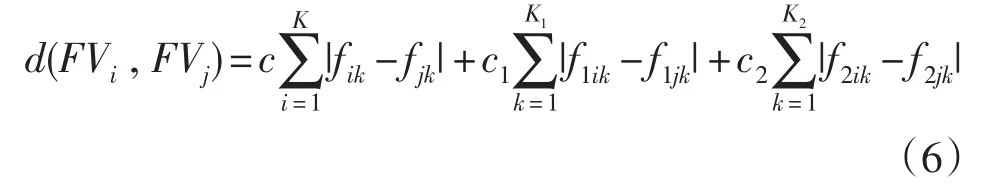
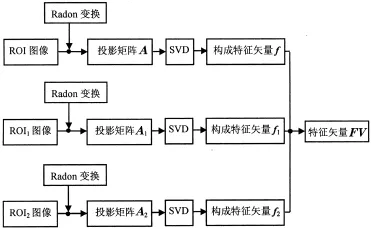
图2　特征提取流程图

其中，FVi，FVj为两个不同手指的指节折痕特征矢量。各权系数值c、c1和c2是根据各部分特征矢量的区分能力来计算的，区分能力越强，对应的权值越大；区分能力越弱，对应的权值越小。

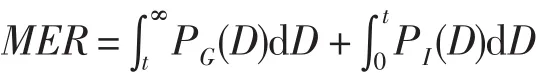
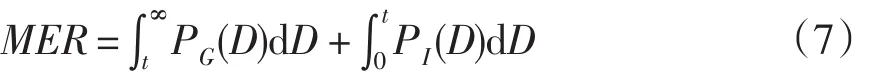
其中，t是两条曲线交点处对应的距离值。

于是，c、c1和c2大小分别由下列三式确定。

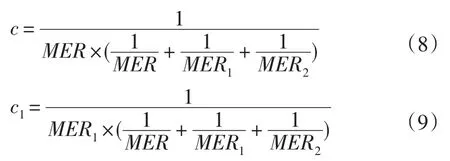
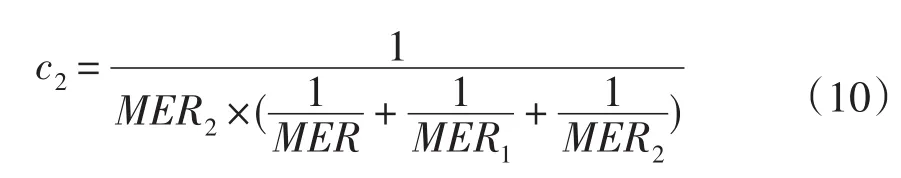
其中，MER、MER1、MER2分别表示ROI部分折痕特征矢量的最小总体错误率、ROI1部分折痕特征矢量的最小总体错误率和ROI2部分折痕特征矢量的最小总体错误率。

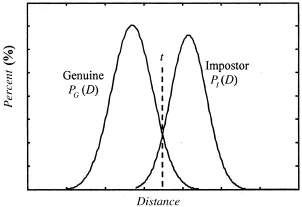
图3　合法匹配和非法匹配距离分

5　实验结果及分析

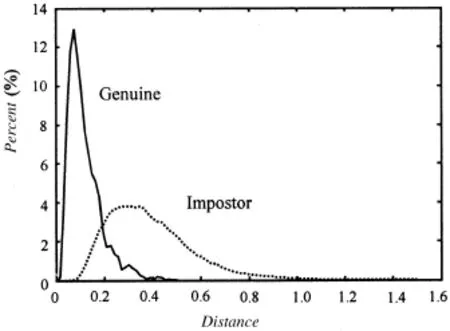
图4　ROI1图像的合法和非法匹配的距离分布

在自行采集的手指图像数据库上对算法进行实验验证。库中拥有来自103个人的共824个（每人共采集8幅）手指图像样本。实验时首先从每个人的中指图像中任取4个样本用来训练，其余4个用来测试。将每一类训练样本的指节折痕特征矢量的均值作为该类的手指指节折痕模板存入数据库，以备后续的匹配和识别实验使用。

由于在匹配前需要确定权系数c、c1和c2的值，所以首先利用数据库中的训练样本来求出各部分合法匹配和非法匹配的城区距离，并将它们的距离分布曲线绘制于图4、图5和图6。从这三个图中可以得出：MER1>MER2>MER。利用式(7)、(8)、(9)和式(10)，可以计算出各部分的权值。最终确定的权值分别近似为：c=0.4，c2=0.37，c1=0.23。从这些距离分布图中还可以看出，非法匹配距离分布曲线的峰值离合法匹配距离分布曲线过近，因此，只单独使用各部分提取的特征时，它们的可区分性不是很好，这主要是因为每一部分的模式过于简单之故，表达的分类信息有限。

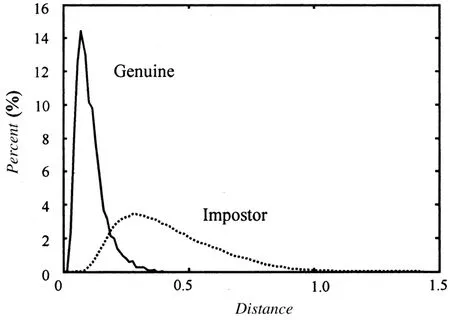
图5　ROI2图像的合法和非法匹配的距离分布

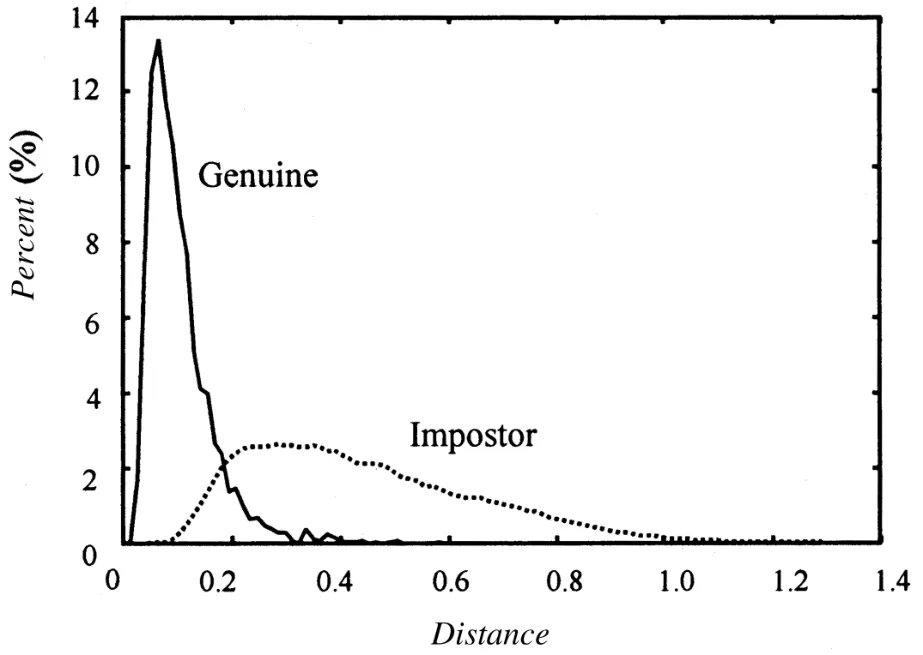
图6　ROI3图像的合法和非法匹配的距离分布

在确定完权系数后，下面来验证算法的匹配区分性能。把每个测试样本和每个模板进行匹配，也就是进行了42 436次匹配，其中103×4=412次是合法匹配，其余的103×408＝42 024次是非法匹配，这二者的距离分布曲线如图7所示。从中可以看出，合法匹配的距离大约集中在0.48，而非法匹配的距离大约集中在1.5。这两条距离分布曲线分得较开，相交区域较少。对比图4、图5和图6，可以欣喜地看到，原来合法匹配距离分布曲线和非法匹配距离分布曲线分布得比较靠近的现象，在这里得到极大地改善，原来不是分得很开的两条曲线现在变成了两条分离得比较理想的曲线，这表明本文提出的特征矢量构成方法和匹配策略是成功的。

为了验证本文算法的鉴别性能，仍然将每个测试样本和每个模板进行匹配，计算出不同阈值t下的拒识率（FRR）和误识率（FAR），从而得到ROC曲线，其曲线如图8所示。由图8可以看出，阈值T＝0.886时，FRR和FAR取值基本相等，错误率（Equal Error Rate，EER）约为1.94%。

在采用基于最小城区距离的分类器实验中，算法的正确识别率(recognition rate)约为98.82%。文献[18]提出的分阶层识别方法，使用了来自73个人的中指进行了算法测试，得到的正确识别率为96.88%。对比可以看出本文算法的优越性。

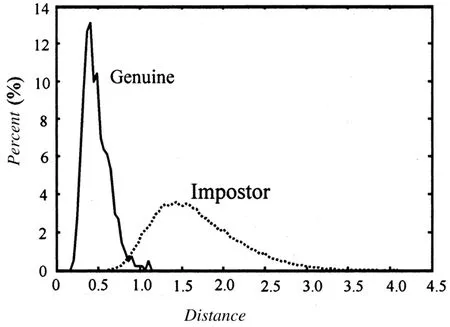
图7　指节折痕特征矢量的类内和类间匹配的距离分布

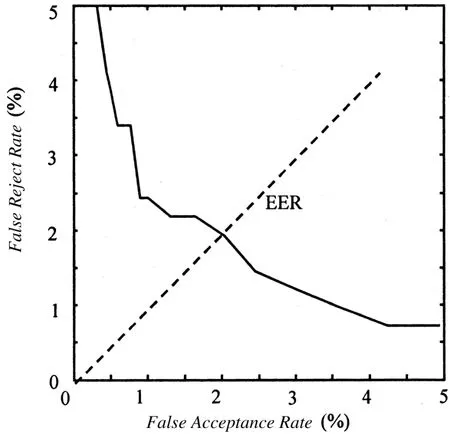
图8　折痕特征的ROC曲线

6　结论

仔细观测指节折痕线分布特点后，可以发现大部分折痕线是分布在几个不同的方向，而Ra⁃don变换可以以不同的方向投影来表征图像，可以满足提取指节折痕特征的需要。因此利用Ra⁃don变换将ROI图像沿几个不同的方向上投影到一维空间，既可以使运算量减少，又能有效地表征折痕特征。用不同角度的投影数据构成的投影矩阵因Radon变换的特点赋予其具有对噪声不敏感的特性。由于从整个手指指节折痕图像通过变换所求出的投影矩阵，代表的主要是全局信息，其描述局部信息的能力是有限的。为了刻画指节折痕的局部信息，在运用Radon变换之前，先将ROI图像等分为ROI1和ROI2两部分，第一部分只包含第一指节的折痕，第二部分则只含有第二指节的折痕。这样可以得到代表整个手指指节折痕的投影矩阵A、代表第一指节折痕特征的投影矩阵A1和代表第二指节折痕特征的投影矩阵A2。然后利用奇异值分解方法对三个投影矩阵进行奇异值分解，从而依据一定的组合策略得到指节折痕特征矢量。最后，采用城区距离来描述样本间的相似度，在采用基于最小距离分类器的实验中，算法的正确识别率(recognition rate)约为98.82%，结果表明本文研究的算法是可行有效的。

参考文献：

［1］Wang Y，Wu Y.Face recognition using intrinsic faces ［J］.Pattern Recognition，2010，43（1）：3580-3590.

［2］罗荣芳，林土胜.基于离散余弦变换的手指指节折痕识别［J］.数据采集与处理，2008，23（2）：129-134.

［3］LUO Rong-fang，LIN Tu-sheng，WU Ting.Personal recognition with finger crease pattern［J］.Opto-Elec⁃tronic Engineering，2007.

［4］罗荣芳，林土胜.基于投影和小波分析的手指指节折痕识别算法［J］.计算机工程，2008，34（5）：216-218.

［5］Magli E.，Olmo G.，Presti L.L.Pattern Recognition By Means of the Radon Transform and the Continuous Wave⁃let Transform［J］.Signal Processing，1999（73）：277-289.

［6］Milanfar P.，Karl W.C.，Willsky A.S.A Mo⁃ment-Based Variational Approach to Tomographic Recon⁃struction［J］.IEEE Trans.Image processing，1996，5（3）：459-470.

［7］Svalbe I.，Spek D.V.D.Reconstruction Of Tomographic Images Using Analog Projections And The Digital Radon Transform［J］.Linear Algebra and its Applications，2001，339：125-145.

［8］Hendriks C.L.L.，Ginkel M.V.Verbeek P.W.，et al.The Generalized Radom Transform：Sampling，Accura⁃cy and Memory Considerations［J］.Pattern Recogni⁃tion，2005，38：2494-2505.

［9］Cui P.，Li J.，Pan Q.，et al.Rotation and Scaling In⁃variant Texture Classification Based on Radon Transform and Multiscale Analysis［J］.Pattern Recognition Let⁃ters，2006（27）：408-413.

［10］Seo J.S.，Haitsma J.，Kalker T.，et al.A Robust Image Fingerprinting System Using the Radon Transform ［J］.Signal Processing：Image Communication，2004（19）：325-339.

［11］Al-Shaykh O.K.，Doherty J.F.Invariant Image Analy⁃sis Based on Radon Transform and SVD［J］.IEEE Transactions on Circuits and Systems，1996，43（2）：123-133.

［12］Hou Zujun.Adaptive singular value decomposition in wavelet domain for image denoising［J］.Pattern Rec⁃ognition，2003，36（8）：1747-1763.

［13］Ashin R.，Morimoto A.，Nagase M.，et al.Image Compression with Multiresolution Singular Value Decom⁃position［J］.Mathematical and Computer Modelling，2005（41）：773-790.

［14］Chuag K.L.，Shen C.H.，Chang L.C.A Novel SVD-and VQ-Based Image Hiding Scheme［J］.Pattern Recognition Letters，2001（22）：1051-1058.

［15］Cang Y E，GuruPrasad M H.Robust edge detection for Swiss Ranger SR-3000 range image by singular value decomposition filtering and Hough transform［J］.In⁃ternational Journal of Intelligent Control and Systems，2010，15（4）：41-48.

［16］Wu X.Q.，Wang K.Q.，Zhang D.Wavelet Energy Feature Extraction and Matching for Palmprint Recogni⁃tion［J］.Journal of Computer Science and Technolo⁃gy，2005，20（3）：411-418.

［17］韩笑，徐坤，马驷良.脊波分析在手背静脉识别中的应用［J］.吉林大学学报：理学版，2011，49 （2）：294-298.

［18］Li Q.，Qiu Z.D.，Sun D.M.，et al.Personal Identifi⁃cation Using Knuckleprint［A］.Advances in Biomet⁃ric Person Authentication，5th Chinese Conference on Biometric Recognition，Sinobiometrics 2004［C］.Springer 2004：680-689.

(编辑：阮毅)

Research on Finger Crease Recognition Algorithm Based on Feature Fusion

XU Juan1，LUO Rong-fang2
（1.Department of Mechanical and Electrical Engineering，Guangdong Vocational College of Environmental Protection Engineering，Foshan 528216，China；2.Faculty of Physics and Optoelectronic Engineering，Guangdong University of Technology，Guangzhou510006，China）

Abstract:As well as fingerprints and palmprint，finger crease has characteristics of uniqueness，stability and differentiation，it can be used as a biometric for human identification.According to the distribution and shape feature of finger crease，an algorithm for finger crease recognition based on feature fusion is researched.Firstly，using Radon Transform to transform finger crease sub image，the projection matrix is obtained.Secondly，using the Singular Value Decomposition method to decompose the projection matrix，the feature vector of finger crease is obtained.Furthermore，considering the simplicity of the finger crease，the feature fusion strategy is emphatically researched，which enable combined-feature to have the bigger distinctiveness.In addition，a city distance is defined to measure the similarity between different finger crease feature and the finger crease is matched by the City Block Distance.Finally，the test is performed with the self-built image database and the experimental results demonstrate that the algorithm proposed is feasible and effective.Key words: biometrics; finger crease；Radon Transform; singular value decomposition(SVD)；feature fusion strategy；city block distance

作者简介：第一徐娟，女，1970年生，湖北天门人，硕士，讲师。研究领域：电子信息工程，模式识别。已发表论文12篇。

收稿日期：2015－05－13

DOI:10.3969/j.issn.1009-9492.2015.08.001

文章编号：1009－9492 (2015 ) 08－0001－06

文献标识码：A

中图分类号：TP391