基于分段模糊控制方法的光伏MPPT控制策略研究*
李营(广州铁路职业技术学院,广东广州 510430)
基于分段模糊控制方法的光伏MPPT控制策略研究*
李营
(广州铁路职业技术学院,广东广州510430)
摘要:在对光伏发电系统的电特性进行理论分析的基础上,基于模糊控制思想提出了一种将固定电压法和扰动观察法相结合的分段式光伏MPPT控制方法。通过对固定电压法经验分析确定最大功率点对应电压的取值范围,结合光伏电池的功率-电压特性曲线分析,将MPPT控制分为4个区段,在不同区段采取不同的控制策略,使光伏发电系统能够快速、稳定追踪最大功率。对所设计的分段式模糊控制系统进行了仿真研究,结果显示,系统运行稳定,能够快速响应并较好地追踪最大功率点。
关键词:分段模糊控制;光伏系统;MPPT
*广州市教育局协同创新重大项目(编号:13XT07)
0 引言
随着我国经济社会需求的高速增长,能源消耗逐年增加,煤炭、石油、天然气等传统能源缺口逐年增大。传统能源的消耗同时也给生态环境带来了极大破坏,2013年全国多地长时间重度污染,部分地区污染指数突破测量上限,使国家经济社会发展面临资源匮乏和污染加剧的双重考验。太阳能光伏发电是新能源的重要组成部分,以其巨大的能源储量和环保性被认为是当前世界上最有发展前景的新能源技术[1]。但因太阳能光伏发电转换效率低、成本高、控制复杂等诸多原因,一直没有得到广泛的普及应用。因此,如何通过技术革新提高光伏发电效率,降低成本,生产出既可靠稳定又价格低廉的光伏发电设备,成为近年来众多学者研究的热点问题。
1 光伏发电的等效模型与基本特性
光伏电池的基本原理可看作一个具有光电效应的PN结[2],利用光入射于半导体的光线产生电子与空穴,进而产生两个电极,当外接负载构成回路后,便产生了电能。图1为光伏电池的等效电路图。因单体光伏电池(cell)容量小,因此在实际应用中往往将多个单体通过串、并联形式链接组成光伏阵列(array)[3]。
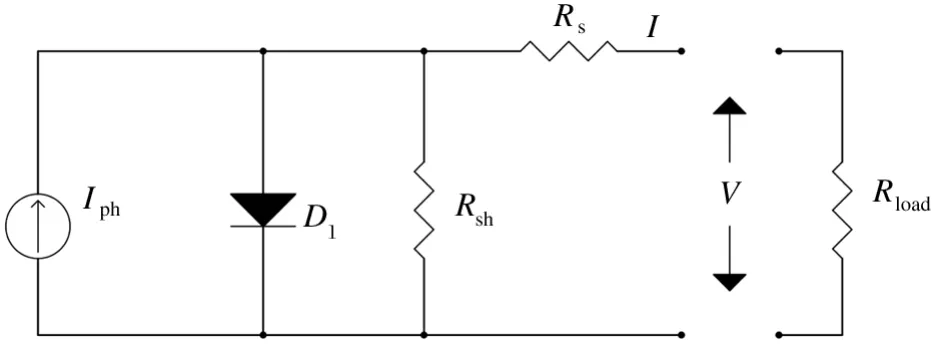
图1 光伏电池的等效电路图
图1的单体光伏电池由理想电流源Iph、串联内阻Rs、并联内阻Rsh和反向并联二极管D1构成,当接入负载Rload后,电池构成回路。其中Iph为光伏电池的短路电流,与外界光线环境有直接关系,光线越强,Iph越大。式(1)为光伏电池的I-V特性函数。
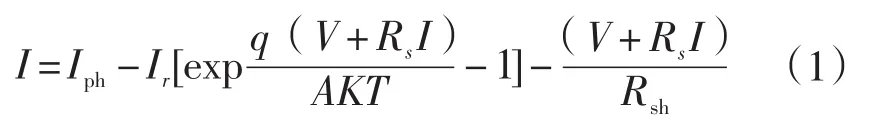
串联内阻Rs为无穷小,并联内阻Rsh为无穷大,因此可以得出:
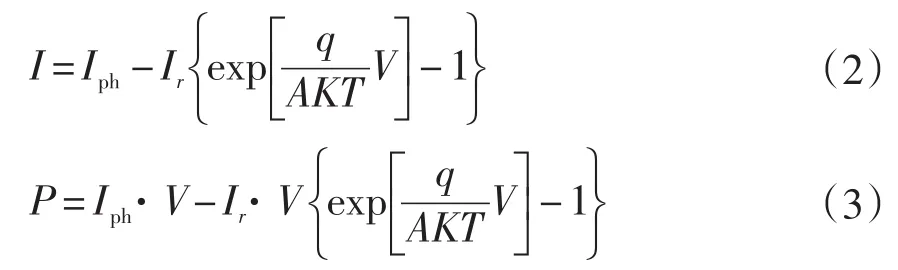
公式中:Ir为内部等效二极管的P-N结反向饱和电流;Vr为热电压,且Vr=AKT/q;K为Boltzman常数;A为光伏电池P-N结的曲线常数;T为光伏电池板温度;q为电荷常数;Rs为串联内阻;Rsh为并联内阻。
由式(2)、(3)可以得出光伏电池具有以下特性:光伏电池的短路电流与光照强度近似成比例关系,开路电压受光照强度影响较小;在同等光强环境下光伏电池最大输出功率随电池温度的上升而下降;在同等光强环境下光伏电池具有唯一的最大输出功率,且最大输出功率随光照强度增强而变大。因此光伏发电中可以采取有效措施对最大功率点进行跟踪控制,使系统长期工作在最大功率状态以有效提高光伏发电的效率。
2 光伏MPPT控制的基本原理与方法
光伏电池是一种非线性的电源,其输出特性可以视为由恒流源与恒压源组合而成,在不同的太阳辐照度下,光伏电池都具有一个最大功率输出点。MPPT控制器的全称“最大功率点跟踪”(Maximum Power Point Tracking),是一种通过调节电气模块的工作状态,使光伏电池能够充分实现光电转换、输出更多电能的电气控制方法,是通过实时采集光伏电池的转换电压,并追踪最高功率(即电压与电流的乘积),使系统以最大功率输出电能的一种自寻优控制技术,是提高光伏发电效率、保证光伏发电系统稳定性的一种有效手段。
目前,国内外关于MPPT控制方法的研究较多,包括直接近似法、固定点压法、扰动观察法、电导增量法、智能控制法以及一些复合算法等[4],各种算法的基本原理和特点如表1所示。由于光伏器件输出功率的非线性特性且其工作环境变化频繁,因此为了获得更好的最大功率点跟踪控制效果,应根据外部环境的变化不断调整MPPT控制参数,在现代控制方法中,模糊控制、神经网络控制等智能控制技术无疑具有这方面的优势。恒压法、扰动观察法和增加电导法均可采用智能控制的方法,根据外部环境的变化调整扰动步长进一步提高控制效果。
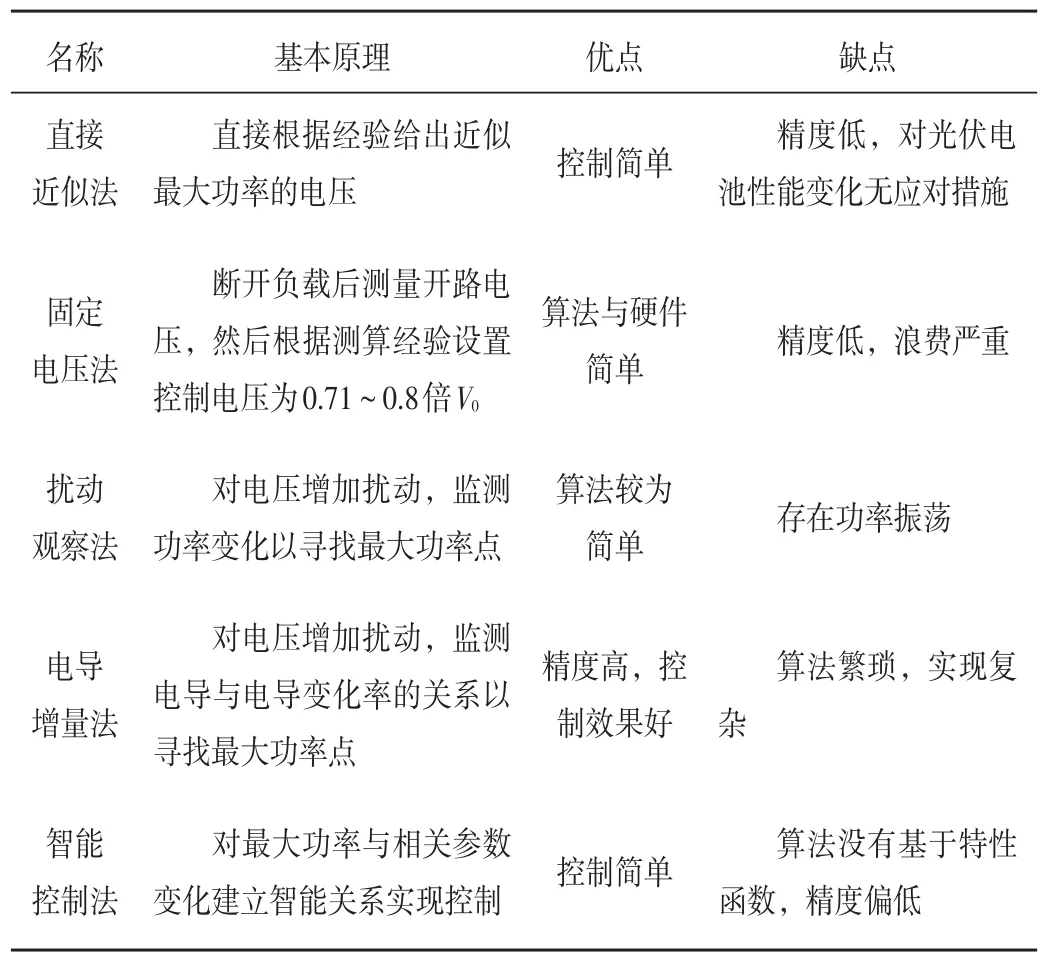
表1 常用MPPT控制方法对比表
3 光伏MPPT的分段模糊控制方法
(1)光伏系统的MPP特性分析
因光伏电池的输出功率与工作电压有关,只有工作在最合适的电压下,它的输出功率才会有唯一的最大值,因此为了分析光伏系统最大功率与电压之间的关系,将(3)式对电压求导,可得出:
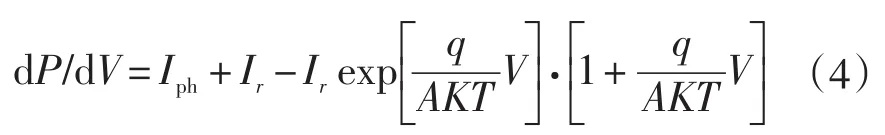
当dP/dV=0时,光伏系统输出最大功率,可以得出:
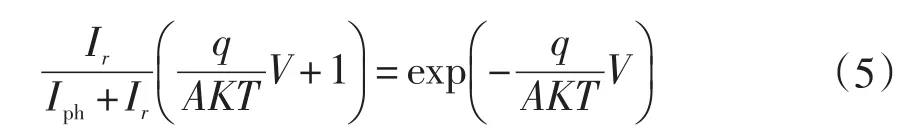
运用Lambert W函数(又称为“欧米加函数”或“乘积对数”)推导算法[5],由ax+b=exp(cx+d)可推导出LambertW函数的显式表达式为:
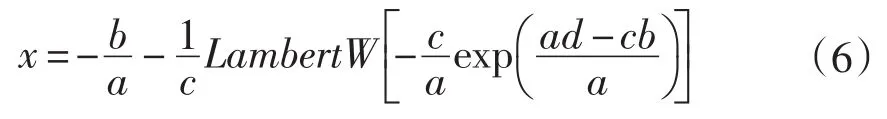
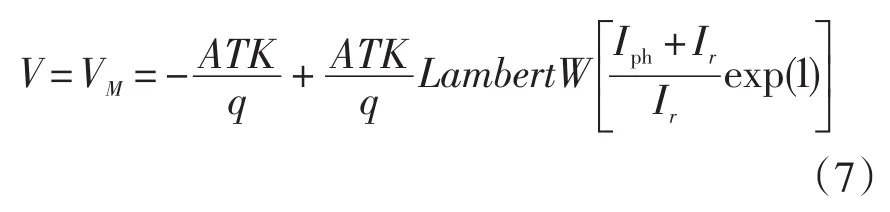
当I=0时,V=V0,将其代入式(2)可得:
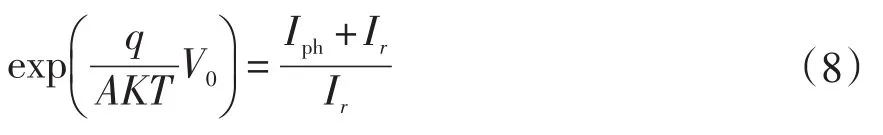
将(8)式代入(7)式并根据Lambert W函数换算法则进行换算可得:
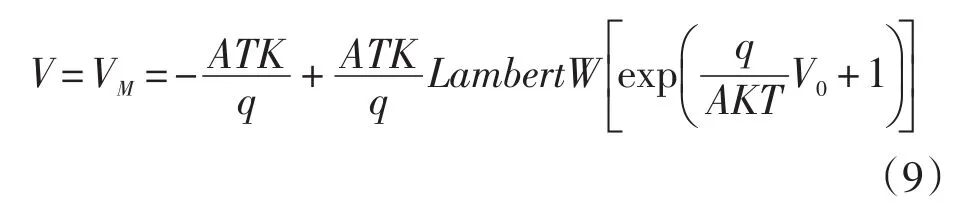
根据Lambert W函数特性:Lambert W [x· exp(x)]=x,可以看出(9)式中VM与V0之间存在近似的比例关系,计为:

MV是与光伏电池相关特性相关的比例常数,仅随自身特性及环境的变化而变化,将MV定义为光伏电池的比例常数,即“电压因子”。MV取值一般在一定范围内,研究经验表明,MV通常是介于0 .71~0 .8之间的常数。因此最大功率点对应电压VM也具有一定取值范围,定义为:VM∈(VMmin,VMmax),其中VMmin=V0·Mv-min,VMmax=V0·Mv-max。
(2)光伏MPPT分段控制策略
根据式(3)和式(4)可以得出光伏系统的P-V特性曲线和dP/dV-V特性曲线如图2(a)和图2(b)所示。
因光伏系统的最大功率点对应电压VM与开路电压存在近似比例关系,且VM取值具有一定取值范围,可以将图2(a)和图2(b)分为4个区段,各区段的划分形式及特点如下:
区段I:dP/dV > 0且V < Vmin,此区段在最大功率点左侧,P-V为近似线性关系,dP/dV趋近于衡定值,距离最大功率点较远,应加大扰动步长使系统快速跨入区段II或区段III内。
区段II:dP/dV≥0且Vmin≤V≤Vmax,此区段在最大功率点左侧,距离最大功率点较近,且距离最大功率点越近dP/dV-V曲线就越陡,此时可通过减小扰动步长使光伏系统的输出稳定在最大功率点附近。控制中可选择ΔP/ΔV和ΔV/V0两个参数作为输入参考变量,以判断现功率点的准确位置,确定恰当的扰动步长。
区段III:dP/dV < 0且Vmin≤V≤Vmax,此区段在最大功率点右侧,距离最大功率点较近,dP/dV-V曲线较陡且随着电压V的增加越来越陡。此区间因功率受电压变化的影响较为明显,控制中可选择ΔP/ΔV和ΔP的变化作为输入参考变量来确定恰当的扰动步长和方向。
区段IV:dP/dV < 0且V >Vmax,此区段在最大功率点右侧,距离最大功率点较远,应通过大步长扰动使系统快速跨入区段II或区段III内。
基于以上分析,可以将光伏MPPT控制的固定电压法和扰动观察法有机结合并融入模糊控制的思想[6],对光伏系统在四个不同区段内采用不同的控制方法。如图2(a)所示,假设系统在I区的M点,因该区段距离最大功率点较远,希望能够通过改变扰动步长使系统尽快接近最大功率点,而最直接的方式就是使其直接跨入II区段,因此可以借助固定电压法的思想,将系统电压直接调整为VMmin,使系统直接进入图2(a)的B点。以此类推,当系统工作在IV区的N点时,也可以通过设置电压为VMmax,使其直接跨入D点;当系统工作在II区段和III区段时,因距离最大功率点变近,采用扰动观察法根据具体位置来设定扰动步长和方向,实现最大功率的稳定捕捉。分区段控制方法对比表如表2所示。
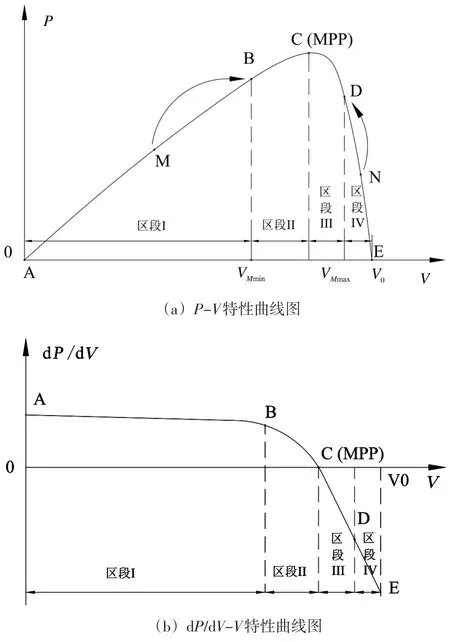
图2 光伏系统的特性曲线图

表2 光伏分区段MPPT控制策略表
(3)分段模糊控制器设计
综合以上分析,在图2(a)的II区段和III区段,采用模糊控制的方法实现MPPT控制。为了获得更好的最大功率点跟踪控制效果,应根据输入参数变化不断调整MPPT电路中的控制步长。控制中,因为二维模糊控制器能够较严格地反映受控过程中输出变量的动态特性[7],并且模糊控制规则简单,因此一般选用P-U曲线上的两点间功率变化与电压变化的比值E和两次采样E的变化CE作为输入变量,选用BOOST升压电路的占空比变化ΔD作为输出变量。但从图2(b)可以看出,在II区段和III区段CE的变化规律不尽相同,在II区段特别是靠近B点附近,因dP/dV-V曲线斜率较小,CE的变化不明显,因此可选取电压变化替代CE作为输入变量,即:
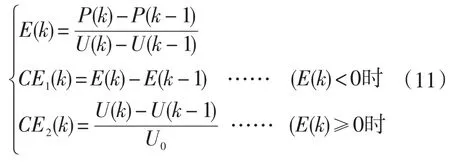
基于既能反映相应的精确量及其特性,又不使推理计算量过大的原则,在光伏电池模糊控制器中选取了E、CE和ΔD的语言词集为负大,负中,负小,零,正小,正中,正大,用英文字头缩写为NB,NM,NS,ZE,PS,PM,PB。为了确保各模糊集能较好的覆盖论域,避免出现失控现象,又不致使计算量过大,取E、CE和ΔD的论域均为:
{-6,-5,…,0,…5,6}
根据光伏发电的特点,选用经验归纳法作为模糊控制规则[8],表3和表4给出了以占空比变化ΔD为控制量输出的模糊控制器控制规则表。
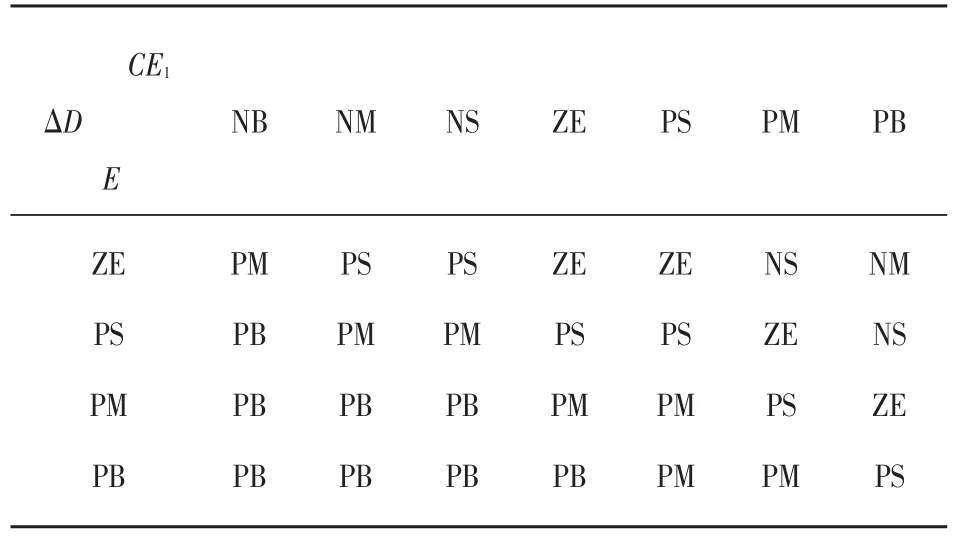
表3 II区段模糊控制规则表
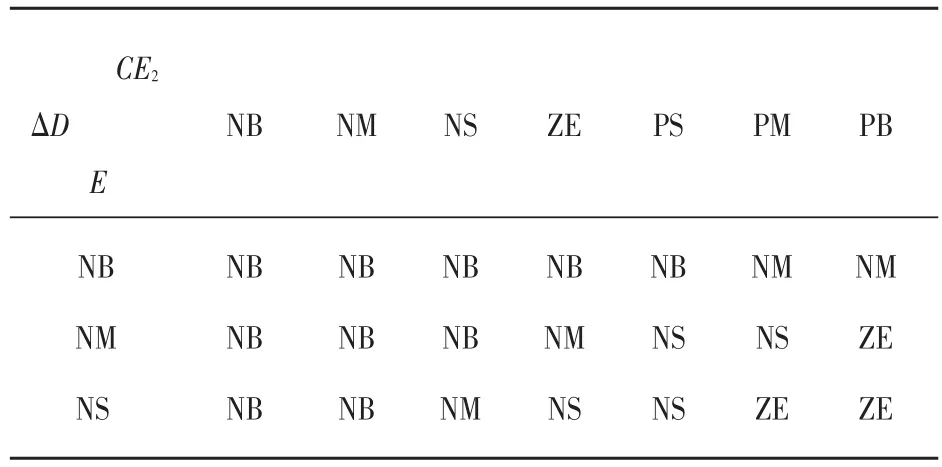
表4 III区段模糊控制规则表
在非模糊化处理中选用面积中心法进行计算,其计算公式如下式:
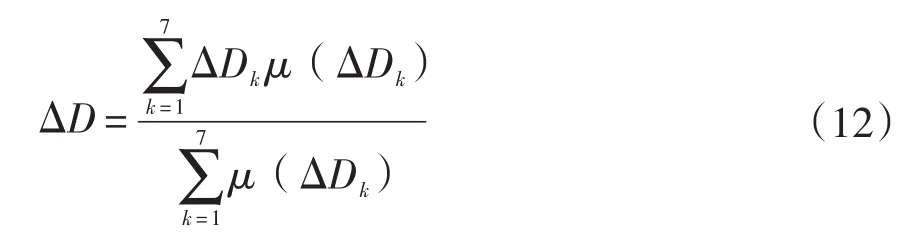
4 系统仿真
为验证分段模糊控制方法的效果,应用Mat⁃lab软件对系统进行了仿真研究,仿真系统模型如图3所示。图中独立式光伏电池等效电路被集成在PV module模块中,分段式模糊控制算法封装在MPPT piecewise fuzzy control模块,BOOST电压变换电路集成在DC-DC module模块。
仿真中选取BOOST斩波开关频率为5 kHz,MPPT周期为3 ms,光伏电池额定功率150 W。环境条件为,温度为恒温25℃,光照强度给出三种变化,即开始为零,1 s后增加到1 000 W/m2,3s后降为300 W/m2,之后保持在300 W/m2。图4和图5分别给出了功率变化和BOOST占空比变化的仿真曲线。
从仿真结果可以看出,采用分段模糊控制可有效提升光伏系统追踪最大功率点的跟踪速度和稳定性,在光照变化时,可以快速响应并减小系统的误判,使系统快速稳定在新的最大功率点。相对于传统扰动观察法和固定电压法,既能简单有效地实现最大功率点的捕捉和跟踪,又能保证跟踪的精度和稳定性。
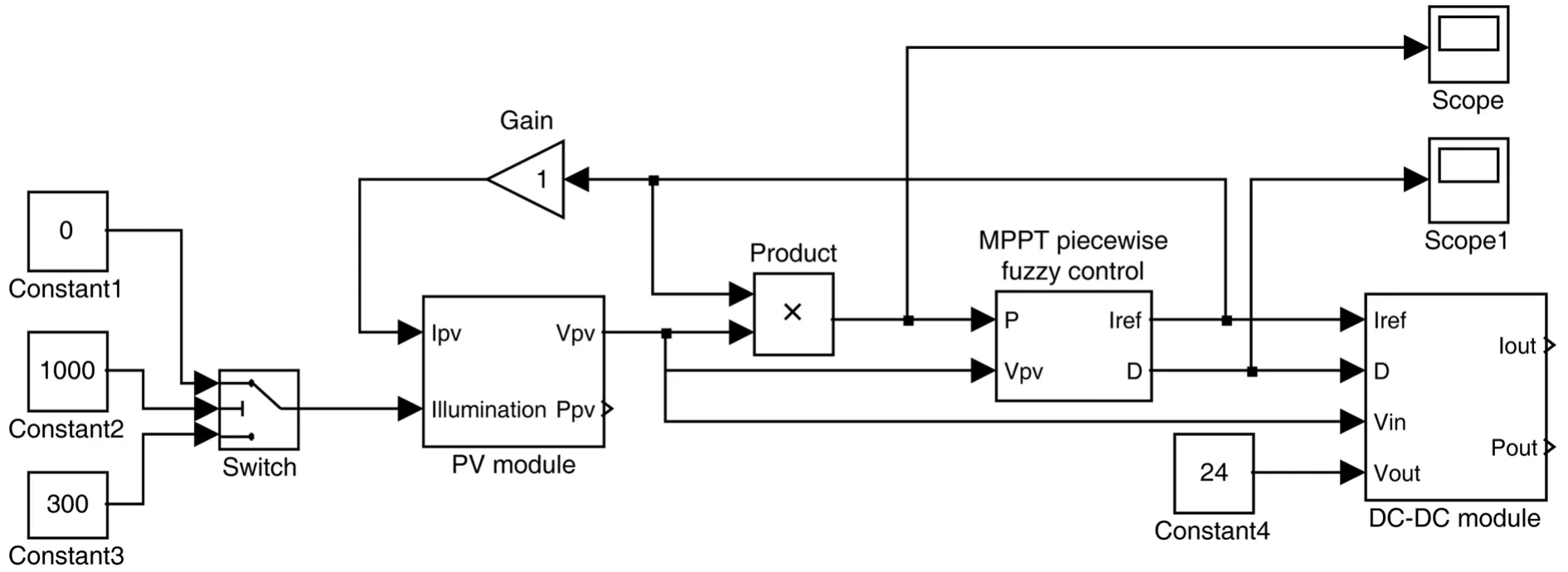
图3 系统仿真模型图
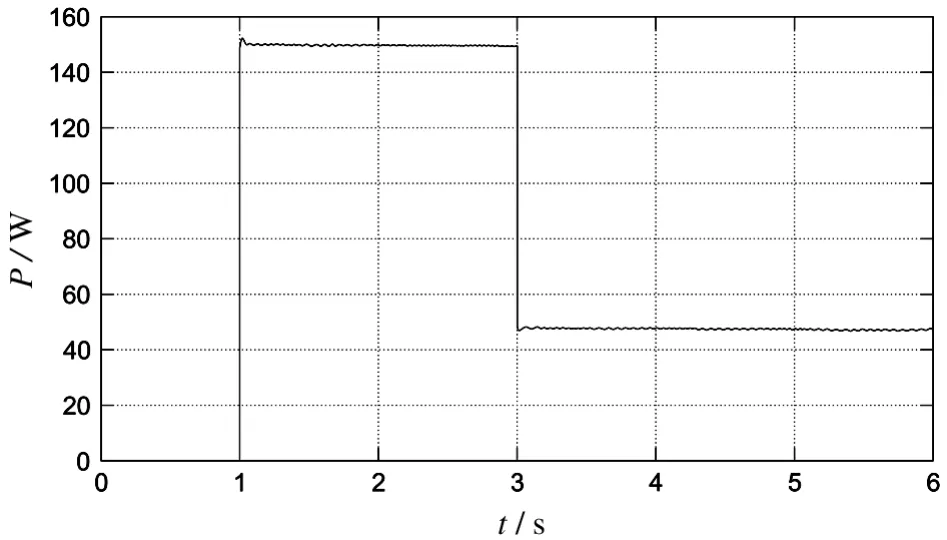
图4 功率输出曲线图
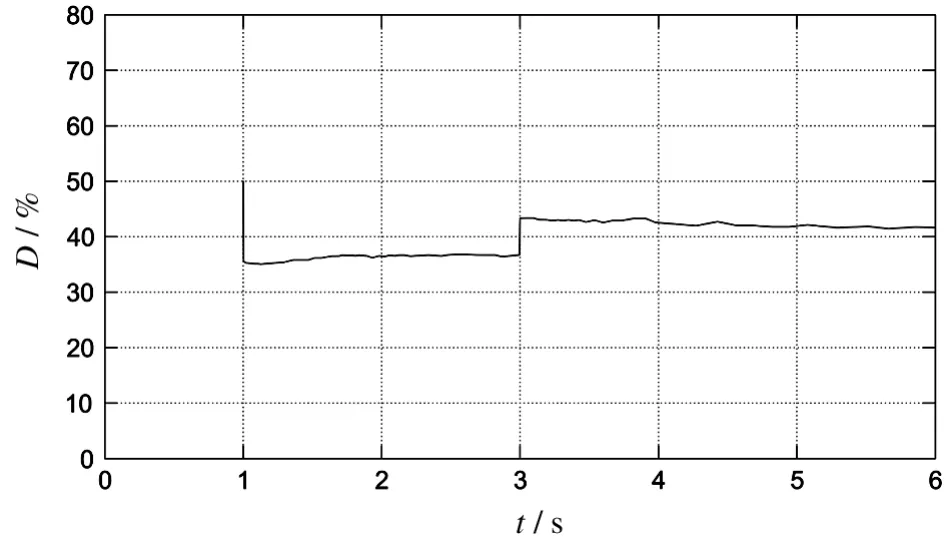
图5 占空比输出曲线图
5 结束语
因真实的光伏发电系统具有数学模型复杂、光照输入多变、受环境影响大、功率输出非线性等诸多特点,捕捉最大功率所采用的固定电压法、扰动观察法、电导增量法、智能控制法等方法各具特点,采用模糊控制方法可有效解决系统难以建立精确数学模型问题,从而简化控制算法。基于光伏发电系统在最大功率点左右两侧所表现出特性的偏差,在最大功率点左右两侧及不同区域采用差异化控制方式可使控制系统进一步提高效率和控制精度。因此将固定点压法、模糊控制方法和分段控制策略结合,建立复合型光伏MPPT控制方案是改善光伏发电系统MPPT控制性能的有效途径。
参考文献:
[1]朱艳伟.光伏发电系统效率提高理论方法及关键技术研究[D].北京:华北电力大学,2011.
[2]吴春华.光伏发电系统逆变技术研究[D].上海:上海大学,2008.
[3]KashifIshaque,Zainal Salam,Hamed Taheri,et al.Maximum Power Point Tracking for PV system under par⁃tial shading condition via Particle Swarm Optimization [C].Applied Power Electronics Colloquium(IA⁃PEC).Johor Bahru,Malaysia.2011:5-9.
[4]张超.光伏并网发电系统MPPT及孤岛检测新技术的研究[D].杭州:浙江大学,2006.
[5]王玉玲.基于LambertW函数的太阳能电池组件参数确定法[J].物理学报,2012(24):1-6.
[6]戴亦宗,赵德安.基于遗传算法模糊控制的光伏发电系统最大功率点跟踪技术的研究[J].机电工程技术,2013(9):56-59.
[7]李营.基于脉宽调制方法的超声马达自适应模糊控制研究[J].制造业自动化,2012,7(7):67-70.
[8]李士勇.模糊控制·神经控制和智能控制论[M].哈尔滨:哈尔滨工业大学出版社,1998.
(编辑:向飞)
Research on MPPT Control of Photovoltaic System Based on the Piecewise Fuzzy Control Method
LI Ying
(Guangzhou Railway Polytechnic,Guangzhou510430,China)
Abstract:This paper analyzes the electrical characteristics of PV system,presents a piecewise fuzzy MPPT control method with a combination between constant voltage method and perturbation and observation method.Through the analysis of the constant voltage method and the power-photovoltaic characteristic curve,determined the corresponding voltage range of maximum power point and divided the MPPT control into 4 sections,adopt different control strategies in different sections.A simulation study was conducted.The results show,the system is fast response and running stable,maximum power point tracking effect is good.
Key words:piecewise fuzzy control;photovoltaic system;MPPT
作者简介:李营,男,1980年生,河北承德人,硕士,工程师/讲师。研究领域:机电系统控制技术、机电一体化技术。
收稿日期:2015-07-17
DOI:10.3969/j.issn.1009-9492.2015.08.023
中图分类号:TP273
文献标识码:A
文章编号:1009-9492 (2015 ) 08-0082-05

