军用补给舰船路径规划改进混合算法

孔垂超，田景文，高美娟

北京联合大学 北京市信息服务工程重点实验室，北京 100101

1 引言

现代海战消耗物资种类较多，舰只设备损毁量较大，后勤补给负担重，所需后勤物资传送距离远，因此海上军用补给舰船运输路径的选择是军事后勤保障的一项重要任务。时间是决定战争胜负的关键因素之一，如何对军用补给舰船运输路径进行规划，使海战中的军用物资经过军事物流的必要环节高效、准确、及时地运抵战斗舰只从而迅速转化为战斗力，是当前需要研究的一项现实而又紧迫的课题[1]。

从本质上来说，该问题属于VRP（Vehicle Routing Problem）问题，是VRP在军事领域的典型应用，所以军用补给舰船路径规划问题具备VRP的典型特征。

由于路径规划问题是典型的组合优化NP难题[2]，求解较为困难，而且具有广泛的现实应用背景，所以长期以来有大量学者对其进行不断地研究探索，研究人员从最初的精确算法开始，逐步转向更广阔的启发式算法领域，如遗传算法、禁忌搜索算法、蚁群算法等。钟石泉等人提出通过禁忌搜索算法对软、硬时间窗约束的VRP进行求解[3]；Chao提出用禁忌搜索算法对多运输工具型VRP进行求解[4]；Chen等人利用遗传算法对钢铁领域物流配送中的车辆时间表制定及路径选择问题进行求解[5]；龚延成等人利用遗传算法求解物流配送组织过程中的运输工具调度问题[6]；唐炉亮等人针对GPS数据的公众出行路径优化问题提出了一种改进蚁群算法[7]。这些算法在VRP的求解上取得了很大的成果，可以较好地运用于海战军用物资配送的路径规划问题中，但也存在着不少问题和不足，如禁忌搜索算法存在对初始解有较高的依赖性的缺点；遗传算法有局部搜索能力不强，易陷入早熟，总体上可行解的质量不高等缺点，尤其是遗传算法的变异操作是随机的，且个体间无信息交流，导致收敛速度较慢的问题，这在军事应用中是一个致命的缺陷。

遗传算法自从被提出就受到了广泛的关注，有很多研究人员将该算法应用于解决路径优化、任务分配以及无线传感器网络（WSN）路由规划等问题。例如田景文等人提出将遗传算法与蚁群算法相结合来解决无线传感器网络路径优化问题[8]；高美娟等人提出一种改进遗传算法并将其应用于Web文本挖掘[9]；李成博等人提出了一种基于遗传算法的WMSNs多路径多目标优化路由算法[10]；雷霖等人提出了一种基于遗传算法的无线传感器网络路径优化算法[11]；杨开兵等人提出了一种改进的Pareto适应度遗传算法用于解决多目标组合优化的求解问题[12]；孔垂超等人提出了一种将遗传算法与BP算法相结合的改进混合算法应用于车辆路径规划。在这些领域的应用中，遗传算法都表现出了良好的性能，但是遗传算法也存在一些缺陷，例如：由于遗传算法不是采用确定性规则而是采用概率变迁规则来指导其搜索方向，所以其搜索方向的明确性在解决大规模问题时远远达不到要求，导致其在运算过程中收敛速度慢，运算时间长，容易陷入局部最优解，这对于军用补给舰船运输的路径规划来说是极为不利的。

粒子群算法是基于鸟类觅食行为而提出的一种算法，其功能与遗传算法非常相似，也是一种迭代优化算法即系统初始化为一组随机解，经由迭代来寻找最优解，与遗传算法相比，具有收敛速度快，参数设置少，实现方便且不需要梯度信息等优点，且其搜索过程是通过并行性从一组解迭代到另一组解，其粒子运行可以搜索不确定的复杂区域，最重要的是其具有记忆特性，具有良好的搜索方向引导性能，这一特点可以用于弥补遗传算法变异操作无方向性的缺陷。但粒子群算法也有一些缺点，如易陷入局部极值点，搜索精度不高以及数学基础相对较为薄弱等。

本文针对上述遗传算法与粒子群算法的优缺点，对遗传算法操作算子做出了很大改进，然后将两种算法进行结合，将遗传算子引入粒子群算法中，有效提高了算法收敛速度，得到了一种运算效率更高，运算结果更精确的改进混合优化算法。

2 军用补给舰船路径规划数学模型

军用补给舰船路径规划问题实际上是VRP问题在海洋环境中的一个特定实例。因此该问题的数学建模规则跟VRP问题的建模规则是一样的，即明确规定符合约束条件时应派出的舰船数量及各舰船的具体路径，保证按时、按量完成运输任务，同时尽量做到使路径总长度最短。

根据上述数学建模规则，在本文中，军用补给舰船路径规划的数学模型表述如下：某海军基地向k艘舰船运送军用物资，设第i艘舰船的物资需求量为gi(i=1，2，…，k)，由海军基地派出载重量为q的运输舰船承担运输任务。设gi＜q，求满足军用物资运输需求的最短行程路线。

为了有效地进行路线规划，可以事先对需要使用的舰船数目进行估算。在现实情况中，舰船数目的需求量取决于军用物资装卸的复杂程度，装卸越复杂，约束条件就越多，舰船的实际载重量就越小。战斗舰艇自主选择的军用物资运送舰船数目可以由下列公式[13]求得：

其中，n表示所需的舰船数；［］表示取整，为保证舰船数目足够，在取整后再加1；gi代表第i艘舰船的物资需求量；α是参数，且0＜α＜1；q代表运输舰船的载重量。约束条件越多的情况下，物资装船、卸船越复杂，α值就越小，一般取α＝0.85。

用cij表示点i到点j的路程，海军基地的编号为0，各战斗舰船的编号为i(i＝1，2，…，k)，现定义如下变量：

可以建立下列目标函数的数学模型：

限制条件如下：

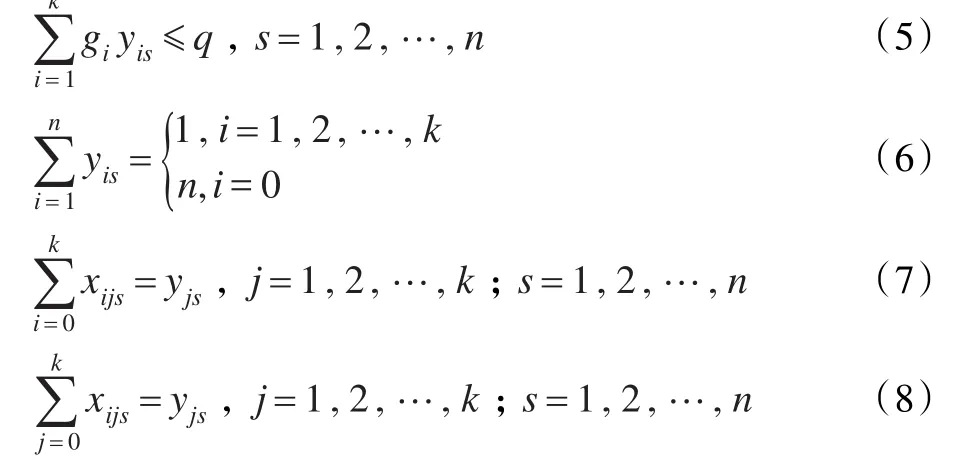
式（4）是以补给舰船行驶路径最短作为目标函数的数学模型。式（5）、（6）、（7）、（8）为该目标函数的约束条件，其中，式（5）表示每艘舰船装载的军用物资总重量不得超过其最大载重量；式（6）是为了保证针对每艘战斗舰艇的配送任务在同一时刻仅由一艘舰船来完成，防止出现多艘补给舰船在同一时刻为同一艘战斗舰艇服务的混乱状况，而所有运输任务则由n艘舰船协同完成；式（7）、（8）保证了到达和离开某一舰艇的货船有且仅有一艘。

由上述数学模型可知该问题是一个典型的多约束条件下的寻优问题，诸如遗传算法等启发式算法在解决该类问题方面具有很大优势，所以本文提出了一种将改进遗传算法与粒子群算法相结合的改进混合算法来对该问题进行求解。

3 粒子群优化算法

粒子群优化算法概念简单，具有很强的较优解搜寻能力，算法比较简洁，易于实现，没有很多参数需要调整，且不需要梯度信息。Eberhart等人已经成功将粒子群算法用于分析帕金森综合症等颤抖类疾病[14]；He等人用改进的速度更新方程训练模糊神经网络[15]。

在粒子群算法中，每个个体称为一个“粒子”，每个粒子对应一个潜在的解。在一个D维的目标搜索空间中，每个粒子被看成是空间内的一个点。设群体由m个粒子构成，zi=(zi1，zi2，…，ziD)为第i个粒子 (i=1，2，…，m)的D维位置矢量，根据事先设定的适应度值函数计算zi当前的适应度值；vi=(vi1，vi2，…，vid，…，viD)为粒子i的飞行速度；pi=(pi1，pi2，…，pid，…，piD)为粒子迄今为止搜索到的最优位置；pg=(pg1，pg2，…，pgd，…，pgD)代表整个粒子群迄今为止搜索到的最优位置。在每次迭代中，粒子根据以下公式更新速度和位置：

其中，i=1，2，…，m，d=1，2，…，D，k是迭代次数，r1和r2为[0，1]之间的随机数，这两个参数用来保持群体的多样性；c1和c2为学习因子，使粒子具有自我总结和向群体中优秀个体学习的能力，从而向自己的历史最优点以及群体内历史最优点靠近。粒子群算法的简化流程图如图1所示。

粒子群算法具有记忆性，较优解的知识被所有粒子都保存，而对于遗传算法，以前的知识随着种群的改变被破坏。在粒子群算法中，信息只来自粒子自身找到的最优位置和群体中的最好粒子，整个搜索更新过程是跟随当前最优值的过程，其方向性较为明确，因此，与遗传算法比较，所有的粒子在大多数情况下可以更快地收敛于最优值。

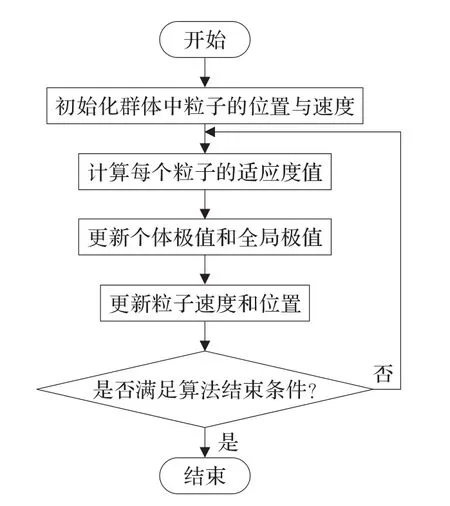
图1 粒子群算法流程图

4 改进遗传算法

遗传算法是一种全新的全局优化搜索算法，以其简单通用，鲁棒性强，适用于并行处理等特点，成为一种被广泛应用的重要启发式算法[16]。但是遗传算法也有较多的缺点，较明显的是其采用概率的变迁规则来指导其搜索方向，导致搜索方向的明确性达不到要求，且其变异是随机的，缺乏方向性，导致收敛速度不快，耗费时间长，这在军用补给舰船运输路径规划中是极为不利的。

本文对传统遗传算法进行改进，在遗传算法的操作中加入克隆操作算子，在选择操作中采用截断选择策略。下面是在本文在改进遗传算法中所采用的操作算子：

（1）选择。本文放弃常用的轮盘赌策略，采用截断选择法进行参数选择，截断选择法是一种人工选择法，适用于规模较大的种群。在截断选择法中，个体按适应度值排序，只有最优秀的个体可以被选作父代个体，截断选择的参数叫做截断阈值Trunc，指的是被选作父代个体的百分比，在本文中，Trunc的取值为10%。在该阈值之下的个体不能产生子个体。

显然，这种选择方式也使得适应度值较高的个体具有较大的“生存”机会。同时，由于它只使用适应度值的相对值作为选择的标准，而与适应度值的数值大小不成直接比例，从而它也能避免超级个体的影响，在一定程度上避免了过早收敛和停滞现象的发生。

在运输舰只路径规划中，染色体即为各种不同的路径，种群即多条染色体的集合，适应度值取路径长度l的倒数。在采用锦标赛选择策略时，路径长度l越短，染色体的适应度值越高，适应度值最高的染色体得以保留作为下一代种群的父代染色体。

选择强度为：

多样化损失为：

选择方差为：

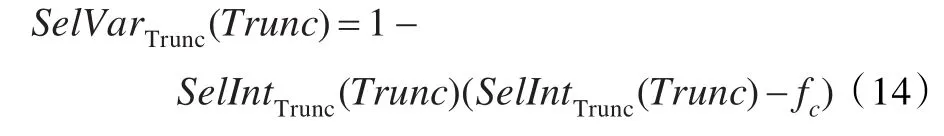
其中fc为下列高斯分布的积分下限：

（2）克隆。克隆操作就是对适应度值较高的个体进行复制，产生一个新的子群体，从而扩大解的搜索范围。本算法中，将由第一步通过截断选择所产生的父代个体进行克隆操作，产生一个新的子代群体，这样便扩大了解的搜索空间。

本算法中克隆算子的定义如下：

设Γc为一个Rn→Rn的映射，如果对任一X∈Rn有Γc(X)=[Γc(x1)，Γc(x2)，…，Γc(xn)]T成立，则称 Γc为克隆算子。

其中 Γc(xi)=Ii×xi，Ii是NCi维行向量，NCi代表克隆的数量，其值可事先确定，也可在算法中动态调整。在上述算法中，克隆的规模与适应度值成正比，既适应度越高，个体被克隆得越多，在这里克隆的数量NCi按下式计算NCi=[βN/i]，i=1，2，3，…，其中，β∈(0，1)是克隆常数，N是种群规模，将个体按适应度度排序，i是其序号。

（3）变异。变异操作是遗传算法中保持物种多样性的一个重要途径，不仅被视为找回因交叉操作而遗失优良基因的手段，还是探索相邻空间、优化性能的有力工具。考虑到VRP问题的实际情况，一般采用自然数形式编码。本文对于新种群的个体采取用Logistic方程对应的概率分布函数来进行变异操作的方案。

Logistic方程对应的概率密度函数如下：

利用该变异操作产生的种群多样度较高，跳出局部极值的能力较强。本算法对适应度值越低的个体所进行的变异程度越高，对克隆所产生的个体进行变异操作，保留原父代个体，从而保证了原有优秀个体，又扩大了解的搜寻范围。

（4）交叉。由于在VRP问题中一般采用自然数形式编码，所以在交叉操作时一般采用离散交叉方式，即在个体之间变换变量的值，子个体的每个变量等概率地随机挑选父个体。

5 改进遗传粒子群混合算法的实现步骤

本文所提出的改进遗传-粒子群混合算法的基本思想是在粒子群算法中引进遗传算法的操作算子，即标准遗传算法的选择、交叉和变异算子，以及本文为改进遗传算法所引入的克隆算子，提高粒子群算法摆脱局部极值点的能力和提高搜索精度的能力，同时将粒子群优化中粒子的飞行引入遗传算法中去，用粒子群公式对每个个体的速度及位置进行更新，并限制其不超过边界，并更新全局最优位置；用粒子群优化公式指导遗传变异，使得变异操作具有更加明确的方向性，按粒子群优化公式对执行变异操作后的个体进一步更新其位置，直到找到达到评估要求的全局最优解。该算法通过将粒子群算法与改进的遗传算法进行结合，实现两种算法的优势互补。

本文提出的改进遗传-粒子群混合算法的实现步骤如下：

（1）随机初始化种群P，种群大小为n，确定每个个体的初始位置和速度；

（2）根据目标函数计算所有个体的适应度值；

（3）若达到结束条件，算法终止；

（4）选择部分适应度值高的个体组成集合Pm；

（5）在Pm中选择适应度值最高的k个个体进行克隆操作得到Pc，克隆的数量与适应度值成正比；

（6）用前文中所提到的改进遗传算法对Pc中的个体进行交叉与变异操作，适应度值越低的个体其变异程度越大；

（7）重新计算Pc中每个个体的适应度值；

（8）按粒子群优化进化公式对Pc中每个个体的速度和位置进行更新，同时限制其不超过边界，并更新全局最优位置；

（9）回到（2）。

在算法的第（8）步，针对变异后的种群，将粒子群优化算法公式引入遗传操作过程，使得个体具有社会性特征，可促进不同个体之间信息的交流，其良好的最优解搜索方向引导性能使得对最优解的搜索具有更明确的方向性，可以弥补遗传算法变异操作无方向性的缺陷，因此可以提高算法的性能；同时，因为粒子群算法需要调整的参数较少，需要评估函数的次数少，不需要目标函数的梯度信息，所以可以提高算法的收敛速度。

改进遗传-粒子群混合算法流程图如图2。

图2 改进混合算法流程图

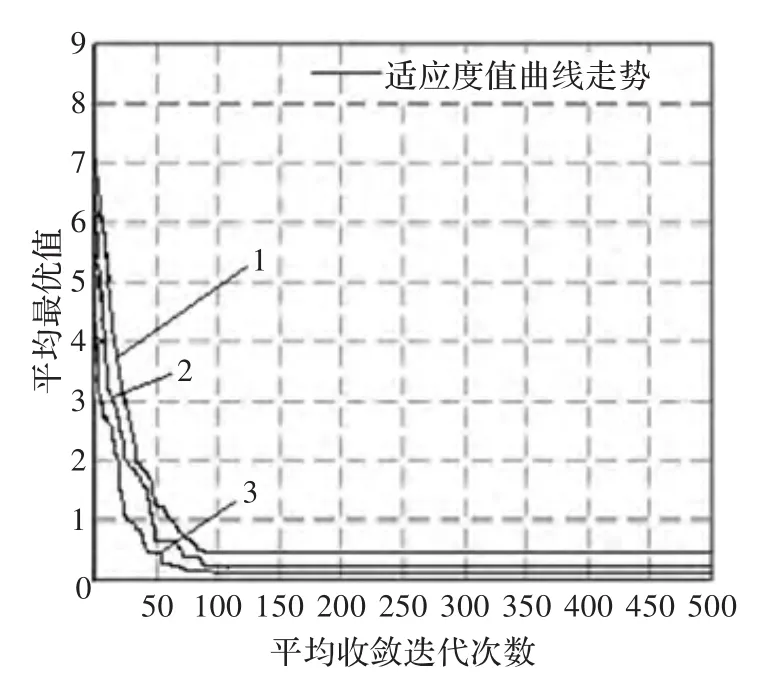
图3 Sphere函数的寻优曲线图

6 仿真结果分析

6.1 仿真实验

本文所做的两次仿真实验均是在MATLAB环境下进行的。

为了验证所提出的改进混合算法的寻优性能，本文选用如下函数进行实验。

（1）Sphere函数：

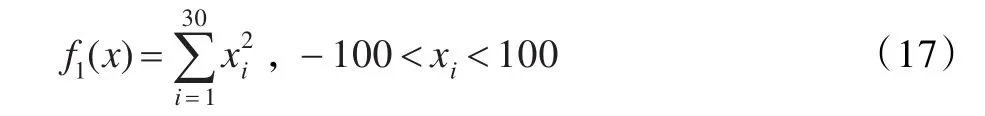
该函数为简单的单峰二次函数。

（2）Rastrgin函数：

该函数是具有大量局部极值点的多峰函数，非常难寻到全局最优值，本次仿真实验的理论最优值为0。

函数f1(x)和f2(x)的标准粒子群算法和改进的粒子群优化算法函数的运算30次平均优化结果，如表1所示；函数f1(x)和f2(x)函数优化曲线分别如图3和图4所示（图中曲线1、2和3分别代表自适应遗传算法、免疫遗传算法和改进混合算法的寻优曲线）。

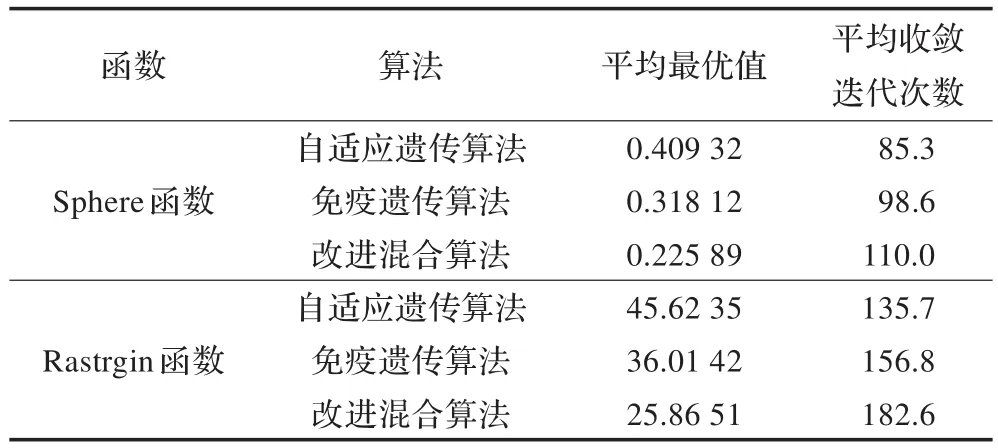
表1 三种算法分别对两个函数进行寻优所得数据

由表1可知，对于Sphere和Rastrgin两个函数来说，本文所提出的改进混合算法比自适应遗传算法和免疫遗传算法具有更好的寻优能力，可以找到更接近理论最优值0的平均最小值，通过数值比较也能看出，改进混合算法的收敛性能和搜索能力也比另外两种算法好。同时，由图3和图4的寻优曲线图可以看出，相比另外两种算法，本文所提出的改进混合算法能达到更小的适应度值，从而扩大了搜索范围和提高了收敛精度；对于较为复杂的Rastrgin函数来说，改进混合算法的寻优曲线也比另外两种算法要平滑，说明改进混合算法稳定性更好，效果也更明显。

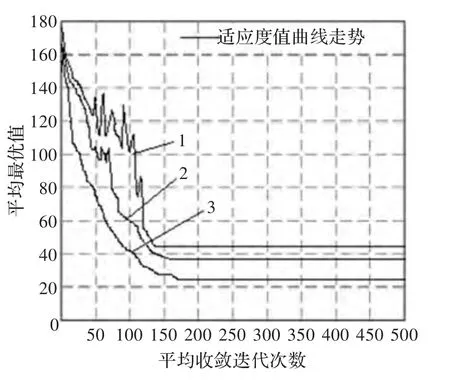
图4 Rastrgin函数的寻优曲线图

在本次仿真实验中，建立一个平面坐标系，选取适当大小的平面区域作为舰船活动区域（为方便计算，本文选取横纵坐标均为100个单位长度的区域作为仿真实验区域）。选择一艘舰船需要遍历的节点数为29，即k=29，加上海军基地共30个节点。分别对自适应遗传算法、免疫遗传算法和本文所提出的粒子群优化遗传算法进行了仿真，以便更好地对本文提出的粒子群优化遗传算法的性能进行对比分析。

在仿真实验中，随机选取的30个节点的坐标分别为（87，7），（91，38），（83，46），（71，44），（64，60），（68，58），（83，69），（87，76），（74，78），（71，71），（58，69），（54，62），（51，67），（37，84），（41，94），（2，99），（7，64），（22，60），（25，62），（18，54），（4，50），（13，40），（18，40），（24，42），（25，38），（41，26），（45，21），（44，35），（58，35），（62，32）。令（87，7）代表海军基地，编号为0，后面依次编号为1，2，…，29。节点编号均在仿真实验所得路径示意图中标出，见图5、图6、图7。

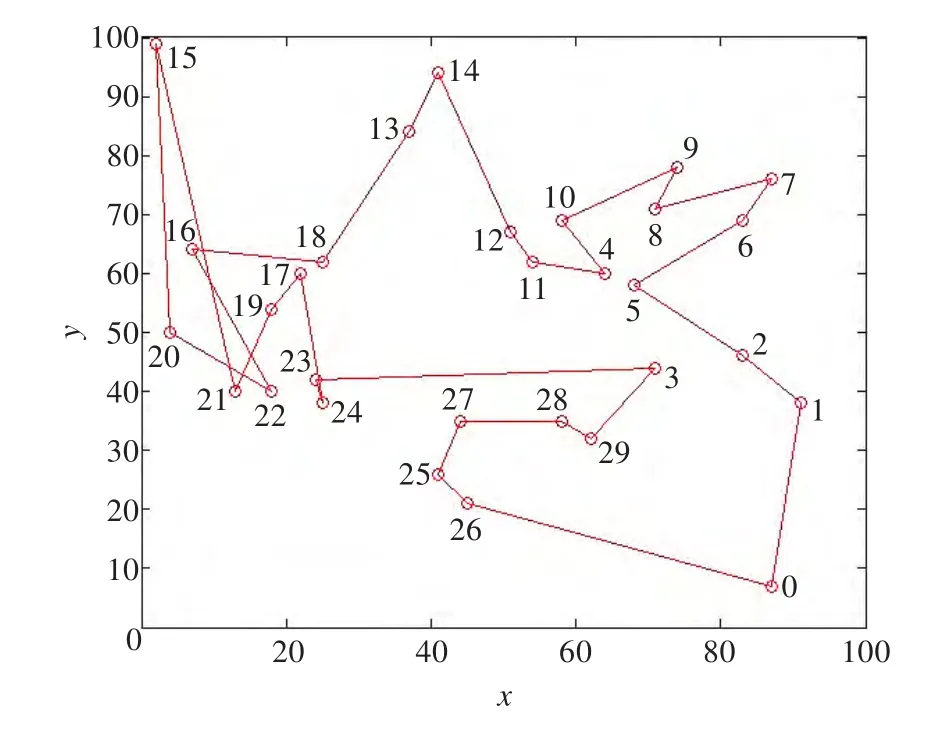
图5 利用自适应遗传算法得到的路径示意图

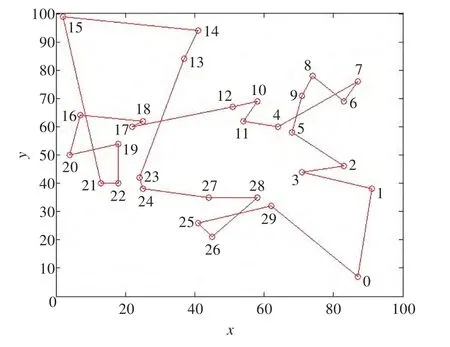
图6 利用免疫遗传算法得到的路径示意图

图7 利用改进混合算法得到的路径示意图

利用本文所提出的改进遗传-粒子群混合算法与免疫遗传算法、自适应遗传算法寻找海上军用物资路径规划的全局最优解。本文的仿真实验以相邻两次优化过程中均方误差的差值的变化率小于等于0.01作为算法终止的条件，此时得到的解已经充分接近最优解，这时算法终止。下面比较三种算法求得的结果，分析其求解性能与效率。

图5、图6和图7分别是三种算法所求得的仿真路径示意图（图中坐标系用于确定节点的位置，使得所求路径便于观察，便于参考路径长度比例关系，所以其坐标值并不是带单位的具体长度）。

利用自适应遗传算法求得的路径为：0→1→2→5→6→7→8→9→10→4→11→12→14→13→18→16→22→20→15→21→19→17→24→23→3→29→28→27→25→26→0。

利用免疫遗传算法求得的路径为：0→1→3→2→5→9→8→6→7→4→11→10→12→17→18→16→20→19→22→21→15→14→13→23→24→27→28→26→25→29→0。

利用改进混合算法求得的路径为：0→1→2→3→28→27→26→25→24→23→22→21→20→18→17→19→16→15→14→10→11→12→13→4→7→6→8→9→5→29→0。

按照以相邻两次优化过程中均方误差差值的变化率小于等于0.01作为算法终止条件的标准，所得实验结果为通过自适应遗传算法在57.1 s的时间内得到长度为523.013 3个单位长度的路径，通过免疫遗传算法在61.8 s的时间内得到长度为492.363 3个单位长度的路径，通过改进混合算法在55.3 s的时间内得到长度为476.384 2个单位长度的路径。

根据实验所得结果可以看出与自适应遗传算法和免疫遗传算法相比，本文所提出的改进混合算法的求解效率是最高的。仿真实验所得数据如表2所示。

表2 三种算法计算所得数据

6.2 实验结果分析与评价

从实例仿真可以看出，本文所提出的改进混合算法相对于其他两种算法能够以更快的速度收敛到全局最优解；求解方面，改进混合算法比其他两种算法找到的路径长度更短，其解的质量有很大提高。说明本文的改进混合算法跟其他两种算法相比，不仅操作简单，而且收敛效果好，收敛速度快，全局收敛率高。

7 总结

由研究车辆路径规划问题（VBR）的算法开始，通过分析遗传算法与粒子群算法各自的优缺点，研究出将两种算法进行结合的改进混合算法，用于解决军用补给舰船运输路径规划的问题。该方法的特点是将粒子群优化算法中加入改进的遗传操作算子，并将粒子群优化公式对遗传变异进行引导，有效提高了遗传算法的寻优效率。本文改进混合算法通过对遗传算法与粒子群优化算法的结合，比较有效地将两种算法的优缺点进行了互补，提高了求解效率与质量。通过在MATLAB环境下利用Sphere函数和Rastrgin函数对自适应遗传算法、免疫遗传算法与改进混合算法的寻优性能进行验证，并进行30个节点的仿真实验，对仿真结果做对比分析，证明本文的改进混合算法在寻优能力和效率等方面要优于其他两种算法，在军用补给舰船路径规划问题的求解中具有求解速度快，所得解质量高的优点，因而本方法是有效且可行的。

[1]杨春周，滕克难.战时舰载导弹配送路径规划模型构建研究[J].舰船科学技术，2009，31（9）：136-140.

[2]宋留勇，王锐，周永旺，等.动态城市交通网络优化模型研究及算法设计[J].测绘科学，2011，36（1）：134-136.

[3]钟石泉，贺国光.有时间窗约束车辆调度优化的一种禁忌算法[J].系统工程理论方法应用，2005，14（6）：523-527.

[4]Chao Yiming.A tabu search method for the truck and trailer routing problem[J].Computer and Operations Research，2002，29（1）：33-51.

[5]Chen Yaorong，Liang Bo，Zhou Meihua.Optimization for vehicle scheduling in iron and steel works based on semitrailer swap transport[J].Journal of Central South University of Technology：English Edition，2010，17（4）：873-879.

[6]龚延成，郭晓汾，尤晓铃，等.基于遗传算法的物流配送车辆调度问题研究[J].数学的实践与认识，2004，34（6）：93-97.

[7]唐炉亮，常晓猛，李清泉，等.基于蚁群优化算法与出租车GPS数据的公众出行路径优化[J].中国公路学报，2011，24（2）：89-95.

[8]Tian Jingwen，Sun Yang.WSN path optimization based on fusion of improved ant colony algorithm and genetic algorithm[J].Journal of Computational Information Systems，2010，6（5）：1591-1599.

[9]Tian Jingwen，Gao Meijuan.Web text mining based on improved genetic algorithm and radialbasisfunction neural network[J].Journal of Computational Information Systems，2012，8（3）：1195-1202.

[10]李成博，王小明，柳强.基于遗传算法的WMSNs多路径多目标优化路由算法[J].计算机应用研究，2012，29（6）：2277-2282.

[11]雷霖，李伟峰，王厚军.基于遗传算法的无线传感器网络路径优化[J].电子科技大学学报，2009，38（2）：227-230.

[12]杨开兵，刘晓冰.求解多目标组合优化的改进Pareto适应度遗传算法[J].计算机工程与应用，2009，45（8）：44-46.

[13]陈迎新.基于改进蚁群算法的车辆路径优化问题研究[J].计算机应用研究，2012，29（6）：2031-2034.

[14]Eberhart R C，Hu X.Human tremor analysis using particle swarm optimization[C]//Proceedings of the IEEE Congress on Evolutionary Computation.Piscataway：IEEE Service Center，1999：1927-1930.

[15]He Z，Wei C，Yang L.Extracting rules from fuzzy neural network by particle swarm optimization[C]//Proceedings of IEEE Congress on Evolutionary Computation，Anchorage，1998：74-77.

[16] 张铃，张钹.遗传算法机理的研究[J].软件学报，2000，11（7）：945-952.