含噪声的海量多元时间序列降维方法研究

刘 博，郭建胜

空军工程大学 装备管理与安全工程学院，西安 710051

1 引言

多元时间序列（Multivariate Time Series，MTS）是在同一个时间点上拥有多个观测值的时间序列。为了得到更加丰富、准确的信息，MTS观测量的维数不断增加，在信息更加准确的同时，也带来了“维灾难”[1]的问题。因此，MTS的降维问题以成为目前时间序列分析领域的一个热点问题。

主成分分析（Principal Component Analysis，PCA）[2]作为一种经典的线性降维算法，在数据挖掘领域得到了广泛应用。PCA方法实际上就是寻找一组相互正交的方向向量（主成分），构成一个低维特征空间，使得原始数据在低维特征空间上的投影能够最大程度地体现差异性[3]。但由于其产生的低维特征空间易受噪声的影响，降低了其学习能力。为了降低噪声对低维特征空间的影响，文献[4]提出了Robust PCA方法，运用迭代法对经典的PCA加权，进而减小噪声的影响。但Robust PCA法时间复杂度大，降低了算法对大样本数据的学习能力。文献[5]提出了一种基于角度优化的全局嵌入算法（Angle Optimized Global Embedding，AOGE），该方法虽然解决了噪声造成的子空间偏移问题，但在非线性数据的降维方面还有待提高。

在MTS的降维研究中，文献[6-9]均是先用PCA方法对数据集中的MTS分别进行降维，然后再进行后续分析。文献[10]引入了共同特征空间的概念，提出了共同核主成份法（Common Kernel Principal Component Analysis，CKPCA）。但是这几种方法均忽视了MTS的高噪声性，影响了其降维效果。

针对上述问题，本文在结合CKPCA和AOGE方法优点的基础上，提出了一种基于角度优化的共同核主成份法（Angle Optimized Common Kernel Principal Component Analysis，AOCKPCA），并将这种算法部署到Hadoop平台上。该方法提高了含噪声的非线性MTS降维的效果，同时也提高了算法对海量MTS降维的能力。最后，通过对比实验，验证了所提方法的有效性。

2 相关研究

2.1 MapReduce编程模式介绍

Hadoop平台是目前主流的云计算平台，为解决海量数据的降维问题提供了一种新的并行解决方案。Hadoop平台的MapReduce编程模式，是Google Map-Reduce算法的开源实现，追求“Moving computation is cheaper than moving data”。在MapReduce编程模式中，开发者仅需设计输入输出的key/value格式，即可实现分布式运算，降低了开发人员的开发难度和强度。MapReduce具体执行过程见图1。

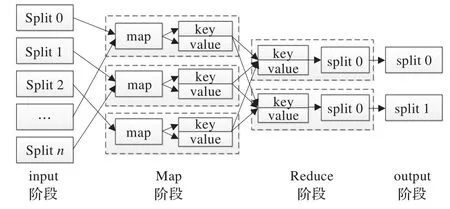
图1 MapReduce运行机制

由于MTS是由各时间点的观察值组成的，且又相互独立，所以MTS数据集可以方便的进行并行分析。依托Hadoop平台，可以将海量的MTS存储在不同的节点上，有利于提高分析效率。

2.2 CKPCA降维模型介绍

CKPCA降维方法是运用MTS数据集的共同特征空间，来消除各MTS特征空间差异给降维带来的影响。共同特征空间是通过共同协方差矩阵得到的，共同协方差矩阵的计算公式：

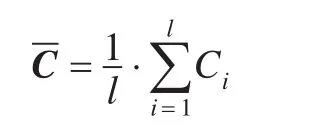
其中，Ci是各MTS的协方差矩阵，l是MTS数据集的容量。该方法的具体步骤：首先通过核函数的非线性映射，将原始序列映射到高维特征空间；再运用点积与核函数的关系，求得共同特征空间；然后按照PCA方法进行降维。

2.3 AOGE降维模型介绍

AOGE方法是利用中心化样本偏离其在低维空间的正交投影的角度来刻画数据之间的关系，消除了基于距离度量对子空间带来的误差。AOGE降维算法构造了有约束的优化模型模型[5]：

3 AOCKPCA降维方法

AOCKPCA方法基本思路：先通过非线性映射，将原始序列映射到高维特征空间；再在高维特征空间上计算基于角度优化的共同子空间；然后再按照PCA方法进行降维。其中，在计算基于角度优化的共同子空间过程中得到的共同主成分被称为基于角度优化的共同核主成分。

由于具体的映射形式和高维空间的维数未知，实现基于角度优化的共同核主成分降维的关键在于：如何将映射到高维特征空间中的数据向基于角度优化的共同核主成分方向的投影，转化为高维空间的点积运算，从而通过核函数实现非线性降维。

3.1 AOCKPCA降维模型

在介绍AOCKPCA降维模型之前，先给出MTS的基本概念[6]：一系列观测值xt(j)称为多元时间序列，其中xt(j)表示第j(j=1，2，…，m)个观测量在第t(t=1，2，…，n)个时间点上的观测值。

下面给出AOCKPCA方法的数学推导。

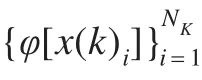
再对已经中心化的观测向量进行单位化，即

则第k个MTS在特征空间F中的M矩阵为：

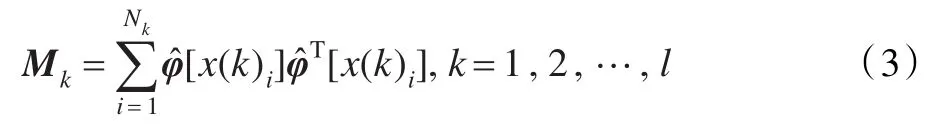
在MTS数据集中，MTS通常具有相同的观测量维数，且各观测量一一对应，具有相同的含义，但时间长度一般不同[10]，所以Mk是一个m×m的矩阵。对l个MTS的M矩阵取平均为：

其中，αj为相关系数。不失一般性，令式（6）中k=1，将式（4）、（6）带入式（5），同时左乘以转置向量(x[1]r)可得：

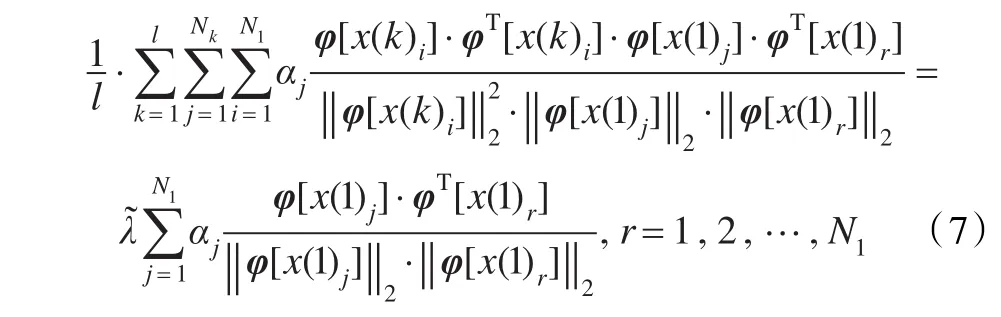
为简化表达式，下面引入两个矩阵定义：

（1）N×N矩阵 Kh，称为核矩阵。其第i行j列上的元素如式（8）所示，其中Kx，y表示φ(x)与φ(y)的内积。

（2）N×1向量a，第j个元素为参数aj。

通过引入核矩阵，式（7）可以简化为：

一般情况下，式（1）不成立[10]，通常采用式（11）中的来代替 Kh。

其中IN是每一元素都为1N的N阶方阵。

由上述模型的数学推导不难发现，若所有观测向量的模都相同（不妨设所有观测值的模均为常数），则核矩阵第i行第j列的元素将变为，此时模型（10）就是CKPCA模型。可见，AOCKPCA算法是对CKPCA算法的推广。

3.2 基于AOCKPCA的MTS降维

对高维共同特征空间F中的特征向量α进行规范化，计算公式为：

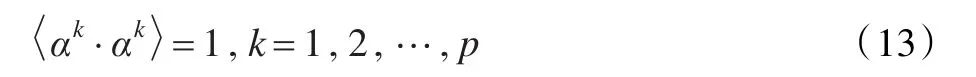
设x是一个待降维的观测向量，在高维公共特征空间F中的映射后为φ(x)，则其向特征向量α投影为：

其中为ak第k各特征向量，是ak的第i个系数。

向高维公共特征空间F中的p个向量依次投影，从而形成降维后的P维向量：

下面给出AOCKPCA降维方法的具体步骤：

（1）选择合适的核函数、确定核函数的形状参数，确定方差贡献率σ。

（2）根据式（8）计算数据集中每个MTS的核矩阵Kh={Kx(h)i，x(1)j}。

（4）求解式（10）表示的特征值问题，并找出全部的实数特征值λi和对应的特征向量αi，根据方差贡献率σ得到p个基于角度优化的共同核主成分。

（5）由式（13），对步骤（4）中求得的p个基于角度优化的共同核主成分进行规范化处理。

（6）p个规范化后的基于角度优化的共同核主成分构成公共特征空间，根据式（14）和（15）将一个MTS依次往公共特征空间上投影，得到p(p＜m)维的MTS序列。

4 AOCKPCA降维方法的并行化改进

由第2.1节的介绍可知，基于Hadoop平台的并行算法设计最主要的工作就是设计和实现Map和Reduce函数，包括输入和输出键值对的类型以及Map和Reduce函数的具体逻辑等。由3.2节的介绍可知，AOCKPCA降维方法的主要计算可以归并成两部分：一部分是计算共同核矩阵，另一部分是求得特征空间后的降维。因此本文分两部分设计Map和Reduce函数，并将这两对函数进行串连，达到并行降维的目的，具体流程如图2所示，图中每一个方框均包含独立的MapReduce任务。

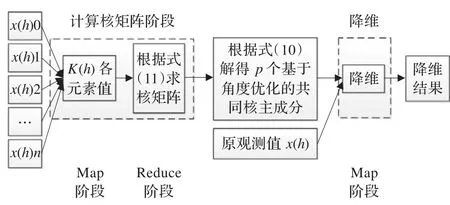
图2 并行AOCKPCA的实现流程

下面给出并行AOCKPCA降维方法的主要设计。

4.1 并行计算共同核矩阵

（1）降维前期处理。在降维前需要首先选定核函数和确定方差贡献率σ。同时为了适合MapReduce计算模型处理，须将待降维的MTS以时间点的向量形式存储，即存储为 ＜h，i，list:v＞ 的形式，其中h表示第h个MTS样本，i表示第h个MTS样本的第i个时间点，list:v为第h个MTS的第i个时间点的上的观察值列表。

（2）Map函数设计。Map函数的任务是根据选定的核函数计算核矩阵各个元素的值。输出为 ＜h， ＜i，j，v′＞＞，其中h是key， ＜i，j，v′＞ 是value，v′是第h个核矩阵第i行第j列元素的值。函数伪代码描述如下：

如因单个MTS的观测量维数过高，可以将观测量分段，依靠多个并行的Map函数并行处理。例如一个MTS的观测向量有900维，现想用3个Map函数并行处理，则可以用第1个Map函数处理第1～300号观测量的相关运算；用第2个Map函数处理第301～600号观测量的相关运算；用第3个Map函数处理第601～900号观测量的相关运算。

同样，如因MTS的时间维数太高，也可按同样的方法进行再并行处理。当然，也可以将MTS同时从两个方向划分，每个Map仅计算其中的一块。

由于MapReduce编程模式的特点，Map函数仅需考虑划分的问题，合并的问题应交于Reduce函数处理。

（3）Reduce函数设计。Hadoop平台可以自动将不同key的Map函数输出传递给不同的Reduce函数[13]。这里因Map输出的key是MTS的编号，所以Hadoop平台自动将的不同的MTS的核矩阵的元素值传递给不同的Reduce函数。然后Reduce函数的主要工作是合并Map函数的运算结果，根据式（11）计算----Kh各元素的值，函数伪代码描述如下：

以上这个Reduce函数是在未建立并行的Map函数的前提下运行的。如前面建立了并行的Map函数，可在开始计算前先将并行的Map运算结果进行合并，然后再运算。例如前面建立了并行的3个Map函数，则在Reduce开始运算前，可先将3个Map函数的对应的输出结果合并，然后再开始计算。

4.2 降维

（1）计算公共特征空间。这一步是在求得共同核矩阵之后进行的，仅需按常规的方法调用API函数编写一个函数即可，这里仅给出具体执行步骤：

①求解式（10）表示的特征值问题，并找出全部的实数特征值λi和对应的特征向量αi。

②根据式（12），得到p个基于角度优化的共同核主成分。

③由式（13）对基于角度优化的共同核主成分进行规范化，构成共同特征空间F。

（2）Map函数设计。在得到公共特征空间后在串联一个Map函数，其任务是根据式（14）和式（15）得到降维序列。输入为 ＜h，i，list:v＞ ，输出为 ＜null， ＜h，i，list:val′＞＞ ，其中list:val′是降维后第h个核矩阵第i行的各值列表，因是最终输出结果，未设key值。函数伪代码描述如下：

因Map函数降维后的输出结果为独立的向量，有利于进一步的并行分析，所以本文未将输出结果用Reduce函数合并成MTS。

5 实验结果与分析

5.1 实验环境

本实验选取5台计算机搭建Hadoop平台，每台机器都是双核IntelCorei3处理器，1 GB内存，操作系统采用国产麒麟操作系统，Hadoop版本选用Hadoop 0.20.2；jdk的版本是1.6.30；一台机器作为Master和JobTracker服务节点，其他机器作为Slave和TaskTracker服务节点。

5.2 实验数据集选取

Australian Sign Language（记为 ASL）数据集包含95种语意（95个类），每种语意都有27组序列，每个序列包含22个变量。实验中σ=80%，选用RBF核函数。

5.3 实验

（1）降维性能实验：降维的目的是为了更有效地利用数据，所以本文采用模式识别的方法测试算法降维的性能。实验采用动态时间弯曲（Dynamic Time Warping，DTW）模式匹配模型，进行k-近邻模式识别。实验在10种语意中，随机选取20组序列作为训练样本，剩下7组序列作为测试样本。测试指标为分类准确率e=n0/n，其中n0为识别准确数，n为待识别样本数。为了测试算法对含噪声数据的分类效果，首先对数据加以均值为0，方差为0.1的高斯白噪声，实验共做了10次，实验结果见图3。

从实验结果可以看出，在对于含有噪声的MTS进行模式识别中，AOCKPCA方法较CKPCA方法有效，有较强的抗噪声能力。

图3 含噪声的MTS模式识别率对比

（2）集群加速比实验：加速比是同一个任务在单处理器系统和并行处理器系统中运行消耗时间的比率，是衡量并行系统或并行化程序性能和效果的主要指标。本文对比了AOCKPCA算法和基于Hadoop平台的AOCKPCA算法处理不同大小数据集时的加速比，实验选取了10种语意，30种语意，60种语意，90种语意的4组数据进行测试，结果如表1所示。

表1 AOCKPCA方法的加速比

从实验结果可以看出，当集群节点数增加时，系统在处理相同数量的作业时性能逐渐提升，当集群节点不变时，系统的性能也稳步提升。但实验中发现，当实验数据较少（10中语意）时，系统性能不如单机性能，这是因为MapReduce编程模型本身存在在大量的I/O操作，影响了运算速度。

（3）集群伸缩性实验：为了验证算法的可伸缩性，分别在由5台和3台机器组成的集群上进行测试并与传统AOCKPCA算法进行对比，实验选取了10种语意，30种语意，60种语意，90种语意的4组数据进行测试，结果如表2所示。

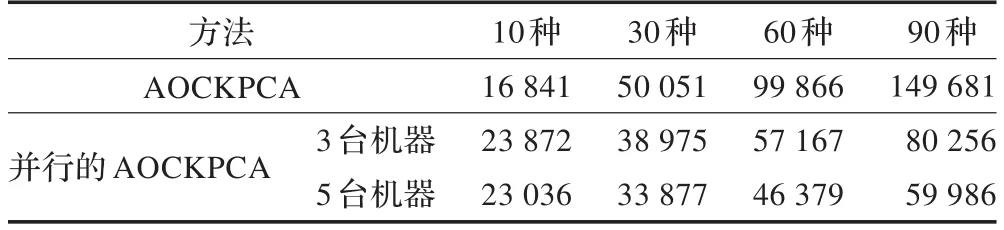
表2 运算时间对比 ms

从表中的数据可以看出，随着数据量的增加，AOCKPCA方法的效率优势会逐步体现，数据集规模越大，优势越明显。当集群中节点数的增多时，算法效率随之增加，节点越多，对数据集规模的增大越不敏感。

5.4 结果分析

通过以上实验可见，AOCKPCA方法较CKPCA方法在针对含噪声的MTS降维运算时，具有更好的表现；在部署到Hadoop平台后，本文所提的算法拥有较好的运行效率和伸缩性，可以有效地运用于含噪声的海量MTS的降维运算。

6 结束语

针对含噪声的海量MTS的特点，提出了AOCKPCA降维算法，并将该算法部署到Hadoop平台，通过实验进行了检验。实验结果表明，在对于含噪声的海量MTS进行降维时，AOCKPCA算法较CKPCA算法更有效，部署到Hadoop平台上后，并行的AOCKPCA方法的执行效率得到了大幅提高，具有良好的加速比和可移植性。但由于MapReduce运算时存在大量的I/O操作，对算法的运行效率影响较大，需进一步优化Map和Reduce两个函数的输入输出，进一步提高运行效率，并需将AOCKPCA算法运行在更大规模的Hadoop集群中以检验其处理海量数据的性能。

[1]Keogh E，Pazzani M.A simple dimensionality reduction technique for fast similarity search in large time series databases[C]//Proceedings of the 4th Pacific-Asia Conference on Knowledge Discovery and Data Mining，Kyoto，2000.

[2]Jolliffe I T.Principal component analysis[M].New York：Springer，2002.

[3]Boente G，Pires A M，Rodrigues I M.Detecting influential observations in principal components and common principalcomponents[J].ComputationalStatistics and Data Analysis，2010，54（12）：2967-2975.

[4]Dela Torre F，Black M J.Robust principal component analysis for computer vision[C]//Proceedings of the 8th IEEE InternationalConference on ComputerVision，Vancouver，Canada.[S.l.]：IEEE，2001：362-369.

[5]刘胜蓝，闫德勤.一种新的全局嵌入降维算法[J].自动化学报，2011，37（7）：828-835.

[6]张军，吴绍春，王炜.多变量时间序列模式挖掘的研究[J].计算机工程与设计，2006，27（18）：3364-3366.

[7]杨兴江，周勇.多元时间序列相似性研究[J].西南民族大学学报，2007，33（4）：864-869.

[8]周大镯，吴晓丽，闫红灿.一种高效的多变量时间序列相似查询算法[J].计算机应用，2008，28（10）：2541-2543.

[9]周大镯，姜文波，李敏强.一个高效的多变量时间序列聚类算法[J].计算机工程与应用，2010，46（1）：137-139.

[10]李正欣，张凤鸣，张晓丰，等.多元时间序列特征降维方法研究[J].小型微型计算机系统，2013，34（2）：338-344.

[11]BhandarkarM.MapReduceprogrammingwithapache Hadoop[C]//Proceedings of IEEE International Symposium on Parallel＆Distributed Processing，2010.

[12]Cheema S，Henne T，Koeckemann U，et al.Applicability of feature selection on multivariate time series data for robotic discovery[C]//Proc of 3rd International Conference on Advanced Computer Theory and Engineering，2010：592-597.

[13]Ziyatdinov A，Marco S，Chaudry A，et al.Drift compensation of gassensor array data by common principal component analysis[J].Sensors and Actuators B Chemical，2010，146（2）：460-465.

[14]Lam C.Hadoop实战[M].北京：人民邮电出版社，2011：85-112.

[15]White T.Hadoop：the definitive guide[M].[S.l.]：O’Reilly Media，2009.