RCC8的一致分割及其算法

崔文正

中国科学院 数学与系统科学研究院，北京 100190

1 引言

区域连接演算（Region Connection Calculus，RCC）是一种用来进行空间定性表示和推理的形式化模型[1]。而RCC8是区域连接演算中最常用的一个子集。RCC[1]最早由Randell等人于1992年基于Clarke利用二元连接关系公理化分体拓扑学（Mereotopology）的工作提出[2-3]，迄今20年取得了一系列重要的理论和应用成果，研究内容包括：RCC及其子集的推理可判定性[4-6]；基于认知的RCC评价[7-8]；RCC推理的复杂度[9-10]；拓扑复合表分析[11]和拓扑关系扩展[12-13]；集成多种空间、方向、时间、位置等信息的定性推理[14-17]等。

RCC8规定了两个空间区域间可能的八种基本关系。这些关系是DC（相离）、EC（外切）、EQ（相等）、PO（部分重合），TPP（内切）和它的逆关系TPP-1，NTPP（真包含）和它的逆关系NTPP-1，图1是这几种关系的示意图。这八种关系两两不相交，并且覆盖了区域之间所有可能的关系，这种性质的关系被称为JEPD（Jointly Exhaustive and Pairwise Disjoint）关系，或者基关系。因为空间中任何两个区域的关系只可能是其中的一种，所以可以用基关系来表示两个空间区域之间确定的知识，而不确定的知识则可以用可能的关系的析取来表示。

表1 RCC8复合运算表

图1 RCC8示意图

表1表示的是RCC8的基关系复合运算(·)表[18]，表中的项目是行与列中基关系的复合结果。如三个区域x、y、z，x和y关系为TPP，y和z的关系为EC，由表中TPP和EC的复合结果，可以得到x和z的关系可能是DC或者EC。*代表全关系，所有基关系的析取。

用约束来指定某两个空间区域间为某个关系。RCC8的约束网络由一个有限的空间区域集合和该集合上有限的约束集合构成[19]。如果两个空间区域在约束网络中没有约束，那么就认为它们的约束是全关系。为了方便使用图论的定理和结果，定义了一种图结构来描述约束网络，称为约束图（见2.1节）。

如果有r⊆R，称关系r是R的细化（refinement）。如果约束图G′与G有相同的顶点集合，且对于任两个顶点在G′中的约束关系r和在G中的约束关系R，都有r⊆R，称G′是G的一个细化[18]。

一个给定的约束图G是一致的就意味着存在另一个约束图G′是G的细化，并且G′中所有顶点之间的约束都是基关系。G′也被称为G的一个一致解。一般求解约束图的一致性是一个NP问题，要用回溯法求解，复杂度是指数级的。

路径一致性是一致性的一个必要条件，它只要求约束图中任何三个区域构成的约束图都是一致的。路径一致性算法的时间复杂度是O(n3)[10]，将路径一致性算法的运行结果称为路径一致性解。RCC8可处理子集指的是可以在多项式时间内求解一致性的RCC8关系集合，如果将约束关系限制在RCC8的可处理子集、C8或Q8的话，路径一致性和一致性等价[9]。

现有的定性空间推理机有GQR[20]、PelletSpatial[21]、PyRCC8-∇[22]。首先利用路径一致性算法对约束图进行路径一致性检查，然后对路径一致性解使用回溯法进行一致性判定。

对大型约束图，求一致性解的回溯法代价太高，即便是路径一致性算法，O(n3)的时间复杂度也是较高的。为了解决大型、稀疏的约束图的一致性检查问题，Huang证明了对于RCC8的可处理子集有Patchwork的性质[23]。Sioutis和Koubarakis利用Patchwork性质将约束图三角化，以此提高路径一致性推理效率[22]。Li和Huang等人讨论了区间代数（IA）和RCC分解的方法[24-25]，但是这些工作只对关系全部为基关系的约束图有效。

本文从图论中的割和割集的概念出发，提出一致分割的概念。目标是在保持一致性的条件下，将一个约束图G分割成若干个不相交的子图，通过检查规模较小的子图的一致性来判断G的一致性，以此降低一致性检查时间。第2章介绍了约束图、分割、Patchwork等的基础知识，并基于此提出了一致分割的定义及其成立的充分必要条件。第3章给出了两个一致分割的充分条件和基于这两个充分条件的高效的一致分割算法。第4章采用随机生成的大型稀疏约束图进行实验，验证了一致分割算法的有效性。

2 一致分割

本章介绍文章的主要内容：约束图的一致分割的定义和充分必要条件。这主要源自于图论中的割的概念和RCC8的Patchwork[23]性质。

2.1 约束图

可以用约束图来表示RCC8的约束网络。一般情况下，约束图应该是一个有向图。顶点v代表空间区域，而v1，v2之间的有向边则代表v1，v2的约束。但如果经过一步预处理，也可以使用无向图来表示约束网络。

对任一个约束网络都可以做如下预处理。假设约束网络中vi，vj的约束为R，vj，vi的约束为Q：若Q和R不互逆，则将vi，vj的约束赋为R∩Q-1，vj，vi的约束赋为Q∩R-1，这样使vi，vj和vj，vi的约束互逆；若Q=R=*（全关系），则删除vi，vj和vj，vi的约束。显然，经过预处理的约束网络仍与原约束网络等价。经过预处理就可以用无向图来描述约束网络。

定义1（约束图）约束图G=(V，E)是一个无向图，V，E分别是图的顶点集和边集，有V={vi|0≤i≤n}，E={(vi，vj，R)|0≤i＜j≤n，(vi，vj)∈R，(vj，vi)∈R-1} 。约束图中没有边连接的顶点对(vi，vj)表示有约束(vi，vj)∈*成立，*为全关系。

定义2（分割和割集）约束图G=(V，E)的分割S=(G1，G2)，其中Gk=(Vk，Ek)，V1∩V2= ∅ ，Ek={(vi，vj，R)∈E|vi，vj∈Vk} ，k=1，2 。 割 集Scut={(u，v，R)∈E|u∈G1，v∈G2}。

定义3（桥）桥是割集元素数为1的分割。

定义4（诱导子图）对于约束图G=(V，E)和其子图H=(V1，E1)，如果V1⊂V，有E1={(vi，vj，R)∈E|vi，vj∈V1}，那么称H为G的诱导子图，记为H=GV1。

值得注意的是诱导子图的这个表示方法将在与Patchwork相关的工作中被频繁用到，它代表的含义就是由图G中一部分顶点和这些顶点在G所有边构成的子图。另外，VG代表图G的顶点集合。

2.2 Patchwork

Patchwork性质：如果两个一致的约束图的一致解在共有的顶点上的约束是相同的，那么这两个约束图的并依然是一致的[23]，如定义5所描述。

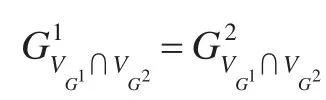
RCC8一致性检查是一种约束满足问题，而且基于RCC8的可处理子集8，C8，Q8的一致性问题是有Patchwork性质的[23]。在下文中如无特殊说明，讨论范围都限定于RCC8可处理子集。

2.3 一致分割及其成立条件

为了描述这种保持一致性的分割，给出一致分割的定义：

定义6（一致分割）一个约束图G的分割是一个一致分割，当且仅当分割成的两个子约束图G1，G2的一致性与G的一致性等价。

可以知道G如果是一致的，那么必然存在一个解S，可知分别是G1，G2的解。所以容易推出一致分割的等价描述。

推论1对于一个分割，如果分割的两个子约束图G1，G2是一致的则G也是一致的，那么这个分割是一个一致分割。

由于在可处理子集中，约束图的路径一致性和一致性是等价的，可以结合RCC8可处理子集的Patchwork性质得到一致分割的充分必要条件：

定理1 约束图G=(V，E)的分割S={G1，G2}，割集为Scut，记。S是一致分割的充分必要条件是：Gs，G1，G2都是路径一致的且对于Gs，G1，G2的路径一致性 解Gs*，G1*，G2*有。

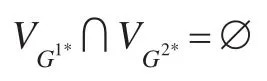
由于Gs*，G1*，G2*是Gs，G1，G2路径一致性解，那么G1∪G2∪Gs满足一致性，则G一致性得证。则由推论1知S为一致分割。

推论2约束图G如果含有若干个连通分量，那么所有连通分量的一致性和G的一致性等价。

这个推论的另一个等价描述是：

推论3如果约束图的割集为空集，这个分割是一致分割。

3 一致分割算法

从上文可知，如果割集中所有顶点的诱导子图的路径一致性解和其他两个分割后的子图的解满足定理1的条件，就可以得到约束图的一致性。

本章主要讨论这个定理的应用方法。3.1节给出了寻找一致分割的算法，并分析此算法的性能。为了提高约束图一致分割的效率，3.2节给出了两种一致分割的充分条件，和相应的高效分割算法。

3.1 一致分割寻找算法

一般的，可以通过检查约束图的所有分割，利用定理1筛选出该约束图的所有一致分割。

一致分割寻找算法：

输入：约束图G

返回：一致分割集合Pc

1.P←{pi|pi为G的一个分割}

2.Pc←∅

3.当P不是空集时：

4. 从P中选取分割pi，并将其从P中删除

5. 利用定理1检查pi是不是一致分割

6.pi是一致分割：将pi加入Pc

7.返回Pc

从定理1的特点和这个算法的过程可以看出直接使用这个一致分割寻找算法有以下两个问题：

（1）一个图的分割个数至少是(2n-1-1)个，所以这个算法至少也是指数级的。显然这并不是一个实用的算法。

（2）充分必要条件不仅要求出分割的两个子图的路径一致性解，也要求出割集相关的顶点在G里的诱导子图H的路径一致性解。如果求解H消耗的时间超过了分别进行一致性求解节约的时间，一致分割就无法减少总时间消耗了。

3.2 一致分割成立的充分条件

这一节给出充分条件来寻找一致分割。这些条件的缺点是不能如一致分割寻找算法找出任何一个图所有的一致分割，但是对某些图它们能高效地找到某些特殊的一致分割。在处理稀疏图或者满足一些特定结构的图的时候，这些条件和其相对应的算法就非常有用。

3.2.1 桥分割

对于割集为桥的分割，有着如下定理所述的性质：

定理2约束图中如果存在着桥，那么以这个桥作为割集的分割是一个一致分割。

这个结论可以使用Tarjan在1974年提出的Bridge-Finding算法[26]，在O(|E|+|V|)的时间内找出所有的桥，将这些桥从约束图G中去除后所有连通分量的一致性和G的一致性是等价的，得到所有连通分量的算法时间复杂度也是O(|E|+|V|)。这样完成一次约束图关于桥的一致分割的时间复杂度也为O(|E|+|V|)。

3.2.2 弱关系分割

先给出弱关系的定义：

定义7（弱关系）RCC8中，如果存在一个基关系r满足如下条件，就定义这个r为一个弱关系：

（1）r=r-1；

（2）∀R，r⊆R·r；

（3）∀R，r⊆r·R；

（4）r·r=*。

注：其中R代表任意一个RCC8关系，*代表全关系。

定理3约束图的割集Gs所有约束中出现的关系集合记为RS，r为RCC8中的某个弱关系。如果∀R∈RS，r⊆R，那么这个分割是一个一致分割。

证明G1，G2都满足一致性，则一定存在一致解G1*，G2*，每个空间之间的关系都是基关系，那么需要证明G是一致的。有∀R∈RS:r⊆R成立，那么RS′是RS的一个细化，其中RS′所有的约束关系都可以细化为r（因为每个关系都包含r）。证明G*=G1*∪G2*∪Gs*是一个G的一致解。

因为G*只是由基关系构成的约束集合，那么可以用检查路径一致性确定G*是否一致。可以任取三点a，b和c∈，列举所有可能的路径。

（1）∀i=1，2:a，b，c∈：三者之间的约束同在Gi*，由Gi*一致性易知路径一致。

（2）三个空间不同在一个空间集合，不失一般性假设：a∈，b∈，c∈。可以知道Rac，Rbc∈RS′，那么由r=r-1知道Rac=Rbc=Rca=Rcb=r，且有∀R，r⊆R·r，r⊆r·R，r·r=R*。所以可以知道Rab无论为哪个基关系，都不会给这三个点构成的任何一条路径带来不一致。由于选取三个点的一般性得知G*是一致的。

由于G*是G的细化，且G*中约束都为基关系，可知G*是G的一个一致解，G的一致性得证。由推论1知满足定理3性质的分割为一致分割。

注意，在定理3的证明中并没有用到可处理子集的性质，说明定理3对于所有的RCC8约束图都成立。

可以从复合运算表中验证DC、PO都是弱关系。所以割集中的关系如果全都包含DC或者全都包含PO的话，这个分割就是一个一致分割。利用弱关系进行判断和分割的算法如下所示，其中遍历算法采用广度优先搜索（BFS）或者深度优先搜索（DFS）皆可，本文以深度优先搜索为例。

弱关系分割：

深度优先搜索（DFS）：

如上所示，分割算法与经典的深度优先搜索算法唯一的不同之处在于增加了第15行的判断：弱关系分割算法将约束关系包含r的边视为不连通。这样使得SG中不同的分割子图之间只有两种可能，要么没有边相连，要么连接两个子图的边的约束关系都包含r，根据定理3这个算法的正确性得证。

另外，由于增加的第15行只有O()1的复杂度，所以这个算法仍然和深度优先搜索算法有着相同的复杂度。根据深度优先搜索的相关结论[27]，可以得出弱关系分割算法复杂度也仅为O(|E|+|V|)。

3.2.3 桥分割和弱关系分割的关系

以上证明了两种一致分割的充分条件，可以看出，这两个条件是互相独立的。在一个约束图里面，可以采用几种不同的分割条件去判断约束图是否是可分割的。

图2给出了一种使用多种分割条件将约束图分割至不能分割为止的流程。该方法先后使用不同的一致分割算法尝试对约束图进行分割，直到分割结果不再满足任何一个一致分割条件。

图2 多分割条件一致分割流程图

值得注意的是图2中三种一致分割算法的调用顺序不会改变最终分割结果。因为三种算法都是将满足某种条件的割集从约束图G中删除，而后将各个连通分量作为分割结果。假设调用一致分割条件顺序为A1→A2→…→An。如果Si是G满足一致分割条件Ai的割集，使用A1，A2，…，Ai-1条件进行分割的话有两种可能：（1）Si中的一部分边被A1，A2，…，Ai-1条件删除，剩下的边构成集合S′i依然是满足一致分割条件的割集；（2）A1，A2，…，Ai-1条件不会删除Si中的边。显然，无论是哪一种情况这个一致分割条件Ai的分割效果都不会被影响。

然而，三种算法的调用顺序对于运行时间会有一定的影响。比如对于图3，如果按照图2中的调用顺序进行分割的话，将进行4次迭代才能将约束图分割到不再可分。而采用DC子图分割→ PO子图分割→桥分割这样的顺序，就只用迭代两次。

从三种分割的算法可以看出，约束图G不能用同一个分割条件连续分割两次。基于这个特点可以得到：

图3 分割条件调用顺序差异带来运行时间差异示例

定理4对于约束图G，利用多分割条件一致分割时，若调用分割条件顺序为A1→A2→A3时，若G在某一次迭代中可以被Am分割，且不能被所有Ai(i＞m)分割，那么下一次迭代只可能：

（1）G不能用任何条件分割；

（2）存在某个条件Aj(j＜m)可以将其分割。

证明情况1，算法此时达到迭代终止条件。

情况2，首先一定存在一个条件可以分割G，否则就落到情况1中。不妨设第一个可以用来分割G的条件为Ak，首先k=m不可能成立，因为上一轮迭代中G被Am分割，其子图不能被Am继续分割；其次m＜k≤3也不能成立，这又与上一轮迭代中G不能被所有Ai(i＞m)分割相矛盾。所以必存在某个条件Aj(j＜m)可以将其分割。

从图2中可以看出每次迭代的时间消耗是一定的，所以迭代次数越少，整个算法时间消耗就越小。

可以看出，降低迭代次数的关键在于增加每次迭代中成功分割的次数。

表2就是最坏情况的迭代示例。调用顺序为A1→A2→A3，且在Ai+1的分割成功之后才能使用Ai分割成功。表格中的行代表分割条件，列代表迭代轮次，其中的成功代表该轮次用对应分割条件分割成功，如果某轮次中所有条件都未被成功调用就代表该约束图已经无法再进行分割。可以看出，平均每次迭代成功分割次数约为1.5次。

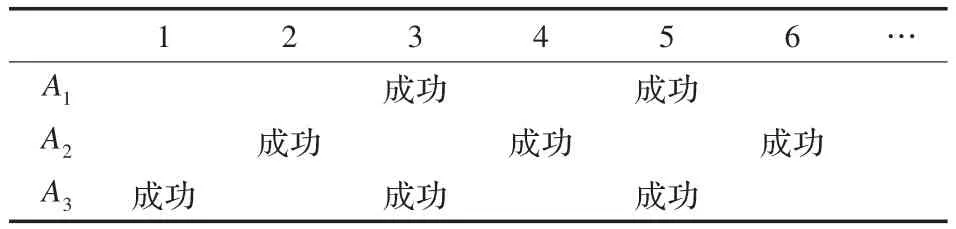
表2 最不利的迭代示例

而如果将调用的顺序改为A3→A2→A1，如表3所示，之后的分割条件正好可以用上之前的分割结果，这样平均每次迭代成功分割次数约为3次。由于成功分割顺序是一样的，两次成功分割总次数相同，那么分割时间之比为2。每一次迭代的复杂度是O(|E|+|V|)，则最有利和最不利的总时间只差O(|E|+|V|)，可知调用顺序对算法的效率没有很大的影响。

表3 最有利的迭代示例

4 实验

本章设计并进行实验，用来验证以上提出的分割算法对于大型稀疏空间约束图一致性检查确实能够起到提高效率的作用。

4.1 实验设计

在实验中用约束图的边数(E)和顶点个数(V)之商D=E/V的值来度量图的稀疏程度，D称为平均度。分别在D=0.5，1，2，3时，观察约束图的路径一致性检查时间和约束图顶点个数的关系。约束图是随机生成的：限定约束图的顶点个数为V(10 000～60 000)，在所有顶点对的集合中随机取出E=V·D个项用边相连，并从8中随机选取关系作为边的约束。

实验环境是：Intel Core i7-2600 CPU 3.40 GHz 8核，内存20 GB，操作系统Fedora 15 64 bit，GCC 4.5.4；推理机采用GQR-1418[20]（同样也可以采用其他的推理机进行实验）。

4.2 实验结果

图4～图7分别表示在不同的平均度下，约束图的路径一致性算法运行时间和约束图顶点个数关系。其中灰柱代表直接用推理机对约束图进行路径一致性检查所用的时间，黑柱代表先利用一致分割进行预处理后，推理机进行路径一致性检查所用时间。没有立柱代表推理机无法处理这个量级的约束图。

从图4和图5中可以看出，在E/V≤1，即约束图十分稀疏的时候，直接使用推理机是非常耗时而低效的；而且当顶点个数多于一定量的时候（50 000），由于内存限制，推理机不能够继续进行。但是如果先进行分割的话，不仅在很高的顶点个数时也能够正常运行，而且运行时间也能一直维持在很低的水平上。

可以看出，随着E/V值的增大，分割后的路径一致性检查运行时间越来越接近直接进行路径一致性检查的时间。在E/V=2时，分割算法依然有很高的效率提高作用，并且能完成直接检查路径一致性不能完成的任务；但是在E/V=3时候，分割算法已经不能解决直接检查无法处理的约束图了，不过此时分割算法还是能够带来可观的效率提高。

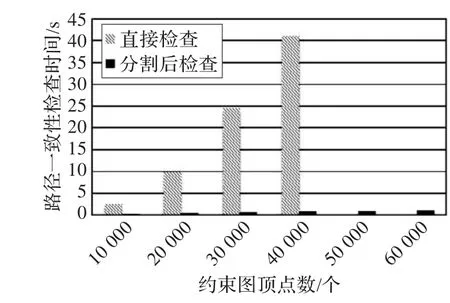
图4 E/V=0.5时路径一致性检查时间和约束图顶点数关系

图5 E/V=1时路径一致性检查时间和约束图顶点数关系

图6 E/V=2时路径一致性检查时间和约束图顶点数关系

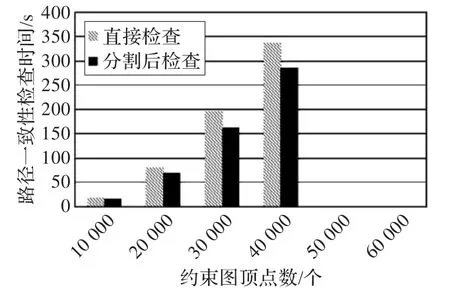
图7 E/V=3时路径一致性检查时间和约束图顶点数关系

从实验结果可以看出两点：对大型的稀疏约束图来说，先进行一致分割所带来的效率提高是非常大的，这说明本文提出的算法是有效的；随着约束图的密度上升分割算法带来的效率提高会越来越小，这是由于一般情况下，越稠密的图分割会越困难，这也表明了本文方法的局限性。

5 结论和工作展望

5.1 结论

本文给出了一致分割的概念，将空间约束图的一致性检查转化为其一致分割子图的一致性检查。

一致分割可以作为RCC约束图的一致性检查推理机[2-4]的预处理过程。对于大型的、稀疏的RCC8约束图一致性检查，可以采用一致分割算法先对约束图进行分割，然后分而检查子图的一致性。本文方法具有以下几个优势：

（1）一致分割算法时间复杂度为O(|E|+|V|)，远低于路径一致性算法复杂度O(n3)。即便面对大型的约束图，也可以用很小的时间代价去检验这个图是否可以分割。

（2）实验过程表明面对稀疏的约束图，如果预先进行一致分割处理，能够大幅度减少总的时间消耗。

（3）对于一些由于内存限制推理机无法处理的大型稀疏约束图，一致分割算法能够将其分割成为若干对推理机来说可处理的子图，使得一致性检查成为可能。

一致分割算法的弱点在于不能够对于所有的约束图都起作用。对于不符合一致分割充分条件的约束图，算法就无法为推理机提高效率了。

5.2 工作展望

一致分割算法还有着很多有待深入思考的问题。首先是一致分割算法在真实数据中的效果。本文的实验数据是随机生成的约束图，对于真实数据是否仍有类似的结论是下一步要讨论的问题。例如RCC可以被用于地理信息的定性描述[28]。地理信息常常有着很强的层次结构，比如洲、国家、省、市、县等，由于高层级的区域之间（比如洲）的约束偏少，这也使得将描述地理信息的约束图一致分割成为可能。

其次，可以将分割后各个子图的一致性检查过程并行化，因为这些过程是互相独立的，所以并行运算可以进一步地提高一致性检查的效率。

另外，一致分割也可以用来确定约束图出现不一致的位置。若要找哪些区域之间的约束引入了不一致性，只需要检查具有不一致性的分割子图中区域之间的关系，而不需要去分析一致的子图。

最后，寻找更多的一致分割条件和算法，对其他的基于JEPD关系的推理演算进行一致分割的探索也都是未来研究的方向。

[1]Randell D A，Cui Zhan，Cohn A G.A spatial logic based on regions and connection[C]//Proceedings of the 3rd Inter-national Conference on Knowledge Representation and Reasoning.San Mateo，USA：Morgan Kaufmann，1992：165-176.

[2]Clarke B L.A calculus of individuals based on connection[J].Notre Dame Journal of Formal Logic，1981，22（3）：204-218.

[3]Clarke B L.Individuals and points[J].Notre Dame Journal of Formal Logic，1985，26（1）：61-75.

[4]Dornheim C.Undecidability of plane polygonal mereotopology[C]//Proceedings of the 6th International Conference on Principles of Knowledge Representation and Reasoning.[S.l.]：Morgan Kaufman，1998：342-353.

[5]Gotts N M.Using the RCC formalism to describe the topology of spherical regions，Technical Report 96.24[R].School of Computer Studies，University of Leeds，1996.

[6]Bennett B.Spatial reasoning with propositional logic[C]//Proceedings of the 4th International Conference on Knowledge Representation and Reasoning，1994：51-62.

[7]Knauff M，Rauh R，Renz J.A cognitive assessment of topological spatial relations：results from an empirical investigation[C]//Proceedings of the 3rd International Conference on Spatial Information Theory.Berlin：Springer，1997，1329：193-206.

[8]Renz J，Rauh R，Knauff M.Towards cognitive adequacy of topological spatial relations[C]//Proceedings of Spatial Cognition II.Berlin：Springer，2000，1849：184-197.

[9]Renz J.Maximal tractable fragments of the region connection calculus：a complete analysis[C]//Proceedings of the 16th International Joint Conference on Artificial Intelligence，Stocholm，Sweden.San Francisco，California，USA：Morgan Kaufmann Publisher Inc，1999：448-454.

[10]Renz J，Nebel B.Efficient methods for qualitative spatial reasoning[J].Journal of Artificial Intelligence Research，2001，15：289-318.

[11]Li Sanjiang，Ying Mingsheng.Region connection calculus：its models and composition table[J].Artificial Intelligence，2003，145（1/2）：121-146.

[12]Cohn A G，Bennett B，Gooday J，et al.Qualitative spatial representation and reasoning with the region connection calculus[J].GeoInformatica，1997（1）：1-44.

[13]欧阳继红，富倩，刘大有.简单凹形区域间空间关系的一种表示及推理模型[J].电子学报，2009，37（8）：1830-1836.

[14]王生生，刘大有，谢琦.集成多方面信息的定性空间推理及应用[J].软件学报，2003，14（11）：1857-1862.

[15]陈娟，刘大有，贾海洋，等.基于MBR的拓扑、方位、尺寸结合的定性空间推理[J].计算机研究与发展，2010，47（3）：426-433.

[16]Li Sanjiang.Combining topological and directional information for spatial reasoning[C]//Proceedings of the 20th International Joint Conference on Artificial Intelligence（IJCAI-07），2007：435-440.

[17]Liu Weiming，Li Sanjiang，Renz J.Combining RCC-8 with qualitative direction calculi：algorithms and complexity[C]//Proceedings of the 21st International Joint Conference on Artificial Intelligence（IJCAI-09），2009：854-859.

[18]Renz J.Qualitative spatial reasoning with topological Information[M].Berlin，Heidelberg：Springer-Verlag，2002.

[19]Bodirsky M，Wölfl S.RCC8 is polynomial on networks of bounded treewidth[C]//Proceedings of the 22nd International Joint Conference on Artificial Intelligence，2011：756-761.

[20]Gantner Z，Westphal M，Wölfl S.GQR—a fast reasoner for binary qualitative constraint calculation[C]//AAAI Workshop on Spatial and Temporal Reasoning，2008.

[21]Stocker M，Sirin E.PelletSpatial：a hybrid RCC-8 and RDF/OWL reasoning and query engine[C]//Proceedings of the 6th International Workshop on OWL：Experiences and Directions，Virginia，USA，2009.

[22]Sioutis M,Koubarakis M.Consistency of chordal RCC-8 networks[C]//Proceedings of the 24th IEEE International Conference on Tools with Artificial Intelligence，Athens，Greece，2012.

[23]Huang Jinbo.Compactness and its implications for qualitative spatial and temporal reasoning[C]//Proceedings of the 13th International Conference on Principles of Knowledge Representation and Reasoning，Rome，Italy，2012.

[24]Li Jason Jingshi，Huang Jinbo，Renz J.A divide-and-conquer approach for solving interval algebra networks[C]//Proceedings on 21st International Joint Conference on Artificial Intelligence，Pasadena，USA，2009：572-577.

[25]Huang Jinbo，Li Jason Jingshi，Renz J.Decomposition and tractability in qualitative spatial and temporal reasoning[J].Artificial Intelligence，2013，195：140-164.

[26]Tarjan R.A note on finding the bridges of a graph[J].Information Processing Letters，1974，2（6）：160-161.

[27]Cormen T H，Leiserson C E，Rivest R L，et al.Introduction to algorithms[M].[S.l.]：MIT Press，2001.

[28]Bennett B.The application of qualitative spatial reasoning to GIS[C]//Proceedings of the 1st International Conference on GeoComputation，1996：44-47.