不完备决策系统规则获取的相容矩阵算法

汪 凌

安庆师范学院 经济与管理学院，安徽 安庆 246011

1 引言

决策规则获取是粗糙集理论及应用研究的一个重要内容。基于粗糙集的决策规则获取本质上是按照属性特征将对象进行分类的问题。目前已有很多文献研究了不完备信息系统的决策规则获取方法。如文献[1-3]给出了基于决策矩阵的增量式规则获取算法，该算法需要计算和保存分辨矩阵的中间环节，时间复杂度较高；文献[4-5]提出了利用上下近似集来填补空缺值并提取决策规则的算法，该算法适用于系统中空值较少的情况；文献[6]提出了基于量化容差关系的规则获取算法，该算法较多地依赖于先验知识；文献[7]给出基于相容关系的不完备信息决策系统规则提取算法，文献[8-9]给出了基于广义决策函数及扩展形式的决策规则获取算法等。但这两种方法都存在一定的局限性，如计算相容矩阵或分配矩阵计算复杂，占用空间大，以及数据集很大时的规则获取效果不理想等[10-11]。针对以上问题，本文根据不完备信息决策系统中相容条件属性矩阵和决策属性矩阵的概念，通过计算分析矩阵，提出一种基于相容矩阵的不完备信息决策系统规则获取算法，并从理论上对算法进行分析。通过实例验证了该算法的正确性和有效性。

2 算法理论基础

2.1 不完备信息系统与广义决策函数

定义2不完备信息决策系统DS=＜U，C∪D，V，f＞，∀∅⊂B⊆C，U上的一个相容关系定义为：

令TB(x)={y∈U|(x，y)∈T(B)}，对于属性子集B而言，TB(x)是与x可能不可分辨的对象的最大集合。

定义3不完备信息决策系统DS=＜U，C∪D，V，f＞，U={x1，x2，…，xn}，B⊆C，广义决策函数 ∂B:U→P(Vd)定义为：

∂B(x)={i|i=f(y，d)，y∈TB(x)}

其中，P(Vd)表示Vd的幂集，∂B(x)表示TB(x)中元素在d上取值集合。

性质1不完备信息决策系统DS=＜U，C∪D，V，f＞，对∀x∈U，若Card(∂C(x))=1，则称DS是协调（或相容、一致）的，否则称DS是不协调（或不相容、不一致）的。

性质2[13-14]不完备信息决策系统DS=＜U,C∪D,V,f＞，设X为具有性质∧(c，v)(c∈C，v∈Vc)的实例集合，Y为具有性质∨(d，w)(w∈Vd)的实例集合，则：

（1）决策规则γ:∧(c，v)→∨(d，w)为真当且仅当X⊆Y，其中C为规则条件部分的所有属性集合。

（2）决策规则γ:∧(c,v)→∨(d,w)(c∈C,v∈Vc,w∈Vd)是最优的当且仅当该规则为真且出现在γ中的合取与析取的真子集构成的任何规则均为假。

由上述定义及性质定理可知，对于任意x(x∈U)，最优规则的决策部分为 (d，w1)∨(d，w2)∨…∨(d，wn)，则有{w1，w2，…，wn}=∂C(x)。

2.2 条件属性矩阵和决策属性矩阵

定义4[15]不完备信息决策系统DS=＜U,C∪D,V,f＞，U={x1，x2，…，xn}，则属性子集B⊆C对应的相容条件属性矩阵MB定义为：

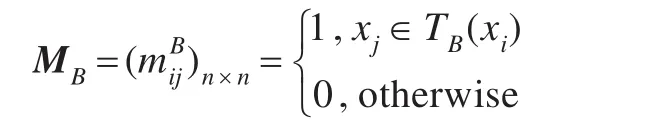
其中，mij为相容条件属性矩阵中第i行j列的元素，i，j=1，2，…，n。

定义5[15]不完备信息决策系统DS=＜U,C∪D,V，f＞，U={x1，x2，…，xn}，DS的决策属性矩阵 MD定义为：

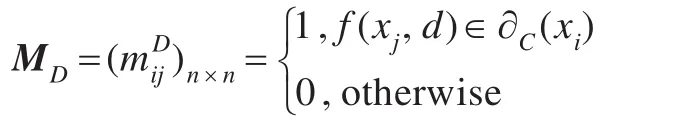
其中，mij为决策属性矩阵中第i行j列的元素，i，j=1，2，…，n。显然，决策属性矩阵是一主对角线为1的n阶对称矩阵。

条件属性子集相容矩阵表述的是该条件属性子集所确定的不完备信息决策系统中所有实例的相容关系；而决策属性矩阵表达的则是所有实例间确定不同决策属性值的区分关系。

在∂C、MB及 MD等定义描述的基础上，可以得出定理1。

定理1不完备信息决策系统DS=＜U，C∪D，V，f＞，U={x1，x2，…，xn}，属性子集B⊆C对应的相容条件属性矩阵，决策属性矩阵 MD=，其中、、(1≤i≤n)是 1×n维向量，上标T表示矩阵的转置。若存在的第i行与的第i行相互一致，则存在一条决策规则：

证明根据条件属性矩阵与决策属性矩阵的定义，如果的第i行与的第i行相互一致，意味着对于条件属性子集B，对象xi与决策不可分辨类D中的任意对象xj之间都是不相容的。反之，如果在决策属性类别中存在yk与xi相容，则有yk∈TB(xi)，所以会存在不一致现象，与相互一致矛盾。因此，对于∀xj∈TB(xi)，f(xj，d)∈∂C(xi)，必然存在一条决策规则：。

定理1表明，当条件属性子集确定的一个实例的广义决策函数值与整个条件属性集确定的广义决策函数值相互一致时，必然能得到一条决策规则，这实际上给出了从不完备信息决策系统中提取相应决策规则集的方法。

3 不完备决策系统规则获取的相容矩阵算法

3.1 算法思想及描述

根据以上命题和定理，提出一种相容关系下基于矩阵计算的不完备决策系统规则获取算法。该算法通过计算相容属性矩阵和决策属性矩阵，当条件属性子集确定的一个实例的广义决策函数值与整个条件属性集确定的广义决策函数值相互一致时，就可直接生成一条决策规则。采用相同的分析处理方法，就可从不完备信息决策系统中提取出全部的决策规则集。不完备信息决策系统中大数据集的决策规则获取流程，如图1所示。

不完备信息决策系统规则获取的相容矩阵算法具体过程描述如下所示。

输入：不完备信息决策系统DS=＜U，C∪D，V，f＞，U={x1，x2，…，xn}，C为条件属性集，D为决策属性集。

输出：DS=＜U，C∪D，V，f＞的所有决策规则集。

步骤1计算DS中条件属性C对应的相容条件属性矩阵MC和决策属性矩阵MD。

步骤3 fori=1ton。

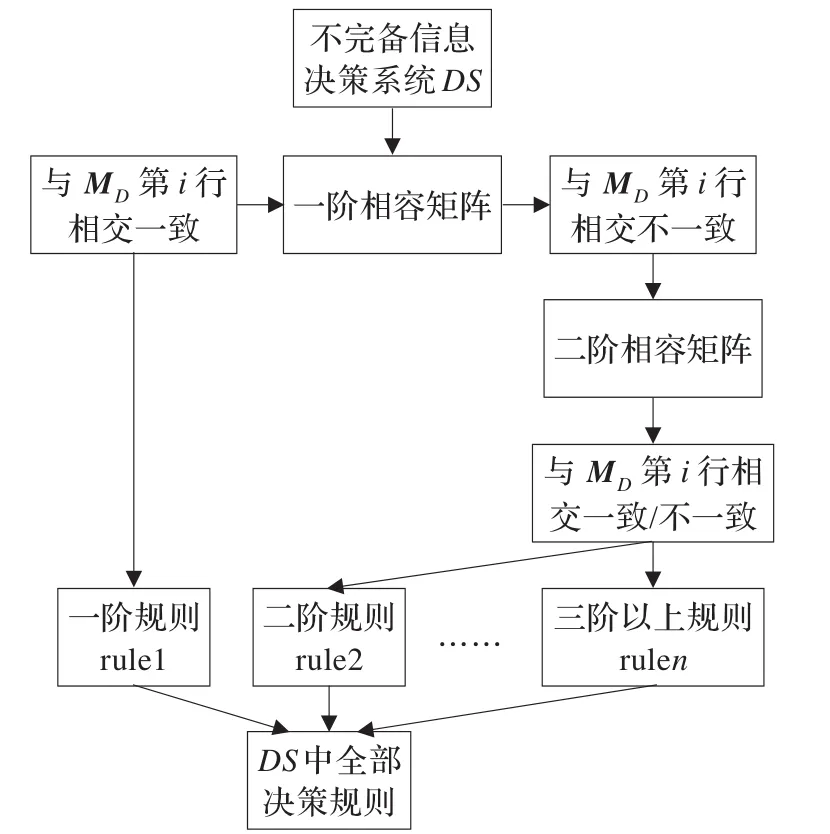
图1 不完备信息决策系统大数据集的规则获取流程

（1）取一阶相容条件矩阵M{c}的第i行与决策属性矩阵MD的第i行相交；

（2）若存在 M{c}的第i行与 MD的第i行不一致，nexti，否则转步骤4。

步骤4根据对象xi的属性第i行对应的属性cm∈C，dn∈D的取值生成决策规则：∧(cm=vcm)→∧(dn=vdn)，同时将第i行置为零，提取出所有的一阶决策规则。

步骤6采用类似步骤5的处理方法提取所有三阶以上的决策规则，直至无非零的同阶相容矩阵为止，最后输出所有的决策规则集。

3.2 算法分析

上述规则获取算法中的相容条件属性矩阵和决策矩阵的生成是执行整个算法的基础。因此，本算法的计算复杂度主要由步骤1～步骤5决定。

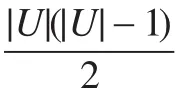
综合以上分析可知，本算法总的计算复杂度为O(|U|22|C|)，计算量的增长相对于对象个数是多项式级的，相对于属性个数是成指数级形式的。

本算法在数据计算量上具有较大的优势，矩阵运算将粗糙集规则提取过程中的复杂比较过程转换成对简单的0、1矩阵或向量的操作，而不是对象集的处理。此外，由于决策属性矩阵只考虑上三角或下三角即可获取相同结果，因而本算法能够减少一半的矩阵计算量，大大提高了算法的效率。

4 实例分析

为了验证算法的有效性，以某城市交通流状态不完备信息决策系统为例计算最小决策规则集。该不完备信息决策系统如表1所示，其中论域U={x1，x2，…，x6}，条件属性集C={F，S，D，L}，其中F表示Traffic Flow，S表示 Average Speed，D表示 Vehicle Density，L表示Team Length，决策属性{d}表示Mode。

表1 城市交通交通流状态不完备信息决策表

表1所示的不完备信息决策表中，存在多个条件属性值未知，因此可以根据上述算法步骤对表1进行如下处理：

（1）根据步骤1，计算不完备信息决策表DS的决策属性矩阵MD和条件属性矩阵MC：

（2）根据步骤2，计算一阶相容条件属性矩阵：

（4）根据算法步骤5，将（3）中所有非零一阶相容条件属性矩阵两两相交，得到如下三个满足条件的所有二阶相容属性矩阵：

对提取的决策规则进行删除、合并等步骤操作，得该不完备信息决策表最终的决策规则集如表2所示。

表2 城市交通流状态决策规则集

决策规则对应的语言描述分别为：

rule1如果该路段或交叉口车辆密度是大，则交通流状态为拥挤的；

rule2如果该路段或交叉口车辆密度是小，则交通流状态为正常的或畅通的；

rule3如果该路段或交叉口车队长度是短，则交通流状态为正常的。

通过提取以上决策规则，即可对城市交通流状态模式进行辨识。将所有决策规则存储于城市交通管理决策支持系统中，则可直接判别出任一时刻的交通流状态模式。

将相同的数据集采用Rosetta Version1.4.41进行规则提取，通过分析比较发现，两种算法得到的决策规则数基本一致，且该矩阵算法减少了计算量，具有较高的运算效率，实例分析表明了该算法的有效性和实用性。

5 结论

决策规则获取是粗糙集理论及应用研究的一个重要内容。现有的决策规则获取算法的低效性一定程度上限制了粗糙集理论的广泛应用，因而寻求高效的规则获取算法具有重要意义。本文基于相容关系下的条件矩阵和决策矩阵，提出一种基于相容矩阵运算的不完备决策系统规则获取算法。该算法在提取规则时减少了矩阵生成的比较次数，降低了矩阵占用空间，通过比较向量大小即可快速求出大数据集的全部决策规则集，因而大大提高了规则获取效率，对于基于规则获取的系统辨识而言具有较强的实用价值。

[1]Liu Yong，Xu Congfu，Li Xuelan，et al.A dynamic incremental rule extracting algorithm based on the improved discernibility matrix[C]//Proceedings of the IEEE International Conference on Information Reuse and Integration.NV，USA.2003.NJ，USA：IEEE Computer Society Press，2003：93-97.

[2]李春生，尹旭日，陈世福.基于Rough集的规则学习研究[J].小型微型计算机系统，2001，22（8）：982-984.

[3]Kryszkiewicz M.Rules in incomplete information system[J].Information Science，1999，113：271-292.

[4]Leung Y，Wu W.Knowledge acquisition in incomplete information system：a rough set approach[J].European Journal of Operational Research，2006，168：164-180.

[5]Hong Tzungpei，Tseng Lihui，Wang Shyueliang.Learning rules from incomplete training examples by rough sets[J].Expect Systems with Applications，2002，22（4）：258-293.

[6]Stefanowski J，Tsoukias A.Valued tolerance and decision rules[M]//Ziarko W，Yao Y.Rough Sets and Current Trends in Computing.Berlin：Springer，2002：271-278.

[7]Ziarko W.Variable precision rough set model[J].Journal of Computer and System Sciences，1993，46（1）：39-59.

[8]黄兵，周献中.不完备信息系统分配约简与规则提取的矩阵算法[J].计算机工程，2005，31（17）：20-22.

[9]Mollestad T，Skowron A.A rough set framework for data mining of propositional defalut rules[C]//Proc of the 9th International Symposium on Methodologies of Intelligent Systems，1996：448-457.

[10]尹旭日，陈世福.一种基于Rough集的缺损规则挖掘算法[J].计算机研究与发展，2000，12（37）：1441-1445.

[11]Komorowski J.ROSETTA：a rough set toolkit for analysis of data[C]//Proc of the 3rd International Joint Conference on Infromation Sciences.SanJose，Calfornia，USA，1997.North Calfornia，USA：Durham，1997，3：403-407.

[12]Wu Weizhi，Mi Jusheng，Zhang Wenxiu.A new rough set approach to knowledge discovery in incomplete information systems[C]//IEEE Proc of the 2nd International Conference on Machine Learning and Cybernetics，2003：1713-1718.

[13]Pawlak Z.Drawing conclusions from data-the rough set way[J].International Journal of Intelligent Systems，2001，16：3-11.

[14]Hu X H.Knowledge discovery in database：an attributeoriented rough setapproach[D].Regina：University of Regina，1995.

[15]Ziarko W，Hu N.Rule discovery from databases with decision matrices[C]//Proc of the International Conference on Methodologies for Intelligent System（ISMIS96），Zakopane，Poland，1996.Heidelberg，Germany：Springer-Verlag，1996：653-662.