基于同态加密技术的安全多方乘积协议

夏 超 ，仲 红 ，2，石润华 ，2

1.安徽大学 计算机科学与技术学院，合肥 230601

2.安徽大学 计算与信号处理教育部重点实验室，合肥 230039

1 引言

安全多方计算[1-2]（Secure Multi-party Computation，SMC）主要研究网络环境下互不信任参与方之间的协作计算问题。通常有多个成员参与协作计算，但目前安全多方计算问题多数局限在两方安全计算问题[3-4]的研究中。文献[5]总结了部分特殊的安全两方计算问题，包括安全两方科学计算、安全两方几何计算、安全两方统计分析等，并指出了多方计算协议由两方协议推广得到的方法。虽然安全多方计算问题的研究取得了一定的成果[6-7]，但是特殊的安全多方计算协议距离应用需求还有很大的差距。安全多方乘积（SMC）正是这样的一类特殊安全多方计算问题。

安全多方乘积作为SMC最基本的运算之一，近年来得到了广泛的关注。文献[8]将一般的多方求积问题转化成求和问题；在此基础上，文献[9]给出一个安全两方乘积协议并应用到除法协议中；文献[10]提出基于签名技术的安全多方乘积协议，可有效地防止攻击者对信息的篡改；文献[11]将普通的数量乘法扩展到矩阵乘法，提出了多方安全矩阵乘积协议并应用到求解线性方程组、矩阵特征值的SMC协议中。现有这些协议因采用茫然传输技术[12]，协议无须第三方的参与，安全性高，在秘密分享、科学计算等安全多方计算领域中具有重要价值。但是，这些多方乘积协议都是由两方协议的扩展得到的，参与方两两之间需要频繁通信，造成协议的通信代价高；而利用茫然传输技术的数据量大，造成了网络带宽消耗大，协议的执行效率低等问题。

多方参与的协作计算中，通信代价是衡量协议性能的重要因素。本文利用同态加密技术，在半诚实模型下，设计了适用于不同通信环境下的串行和并行的安全多方乘积协议。比如，在这样的复杂通信环境中：参与方Alice计算一个中间数据时间为1，而Alice与其他参与方通信一次的时间要远远超过1。此时，参与方之间如果频繁的通信会造成较高的通信代价，不利于协议执行。选择通信轮次少的串行协议可有效的降低通信代价；相反，如果参与方之间通信一次的时间接近或小于1，通信环境较为理想的时候，并行协议能有效地减少参与方的等待时间，提高协议执行效率。

2 预备知识

2.1 同态加密

设加密算法为E(·)，解密算法为D(·)，明文空间M∈Z。如果对任意明文x，y∈M，x+y∈M，不存在多项式时间算法区分E(x)和E(y)，且对任意k∈Z，满足E(x+y)=E(x)E(y)，E(kx)=E(x)k，那么此算法是加同态加密算法。Paillier算法[13]就是这样的一个算法。

2.2 Paillier算法

加密：任意明文m∈Zn，随机选择r∈Z*N，那么密文c=gmrNmodN2。

解密：解密密文c得到明文m=L(cλ(N)modN2)/L(gλ(N)modN2)。

2.3 半诚实模型下的安全性

本文假定各参与方是半诚实的，其安全性定义与文献[14]相同，即n个参与方P1，P2，…，Pn，他们各自拥有xi，在不泄露各自任何信息的情况下合作计算多项式时间函数：

其中fi(x1，x2，…，xn)表示第i个分量。设计算f的协议标记为π，那么Pi(i=1，2，…，n)在执行协议π后得到的视图(x1，x2， …xn)=(xi，ri，vi，1，vi，2， …，vi，m) ，其中ri是Pi随机选择的结果，vi，j表示Pi接收到的第j个消息。协议执行后，Pi得到的输出序列为(x1，x2，…，xn)。

上述各方Pi(i=1，2，…，n)执行协议π能够安全地计算出f，当且仅当下面的多项式时间算法Si(i=1，2，…，n)成立，即：

3 安全多方乘积协议

3.1 问题描述

假设有n个参与方Pi(i=1，2，…，n)，每个参与方Pi拥有一个秘密整数xi。所有参与方希望在不泄露各自秘密的前提下，计算出所有xi的乘积并且由参与方共享计算结果。

3.2 相关符号说明

RANDOM SELECTr1，r2，…，rn，表示选择随机n个整数r1，r2，…，rn；

x→y，表示将变量x赋值给变量y；

SEND(Alice，Bob，s1，s2，…，sn)，表示 Alice将信息s1，s2，…，sn发送给Bob；

Alice COMPUTE，表示Alice进行计算；

Alice GETs，表示Alice获得信息s。

3.3 具体协议

以下给出串行和并行安全多方乘积协议的详细步骤，数据传输流程分别如图1、图2所示。

图1 串行协议数据传输流程

图2 并行协议数据传输流程

协议1串行的安全多方乘积协议

输入：参与方Pi(i=1，2，…，n)拥有整数xi，Pi选择2.2节Paillier算法并产生公私钥(pki，ski)。

协议步骤如下：

协议1中，参与方Pi存在等待时间，改变协议的执行规则，得到协议2。

协议2并行的安全多方乘积协议

输入：参与方Pi(i=1，2，…，n)拥有整数xi，Pi选择2.2节Paillier算法并产生公私钥(pki，ski)。

协议步骤如下：

3.4 协议分析

本节主要针对协议1和协议2的正确性、安全性和效率进行分析。

3.4.1 协议1的性能分析

正确性证明：

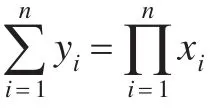
证明 在协议1步骤2中：

根据2.1节加同态性质，Pi解密zn，i得到：

综上所述，协议1是正确的。

表1 安全多方乘积协议比较

安全性分析：

定理2在半诚实模型下，串行多方乘积协议参与方除了得到yi，无法得到其他参与方秘密。

证明设串行多方乘积协议标记为π，通过构造模拟器的方式对π进行安全性证明：

对Pi(i=1，2，…，n)的视图：Pi通过协议π在步骤2中得到由Pi-1发送的数据zi-1，1，zi-1，2，…，zi-1，i-1。对Pi产生视图可记为：

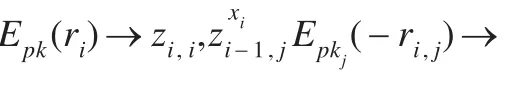
综上所述，串行多方乘积协议是安全的，参与方除了得到yi，无法得到其他参与方秘密。

效率分析：

（1）计算复杂度。假设本协议的数据长度为mbit，Paillier加密方案的模为M，那么一次加密或者解密需要2lbM次模乘，一次模指运算E(x)k最多2m+1次模乘。步骤2中，Pi加密计算i个中间数据，需要i-1次模指运算和i次加密运算，步骤4中进行一次解密运算。所以总计算复杂度为O(n2(m+lbM))次比特模乘运算。

（2）通信 复杂 度。 由步 骤 2 中 SEND(Pi，Pi+1，zi，1，zi，2， …，zi，i) 和 步 骤 3 中 SEND(Pi，Pi+1，zn，i+1，zn，i+2， …，zn，n)可知，协议1的参与方Pi只与Pi+1进行两次通信，发送n个数据。所以总的通信轮次是线性的，带宽O(mn2)。

3.4.2 协议2的性能分析

定理3协议2的正确性、安全性以及计算复杂度同协议1，协议2通信轮次O(n2)，带宽O(mn2)。

证明 在协议1中，参与方Pi一次计算i个中间数据且等全部计算结束之后发送给Pi+1。而由协议2的执行步骤步骤2可知，Pi每当计算出一个中间数据就立即发送给Pi+1。因此，协议2与协议1仅仅是数据流的不同，数据量以及计算方法没有发生变化，所以协议2的正确性、安全性以及计算复杂度同协议1。由定理1和定理2可知协议2是安全正确的。

另外，协议2总数据量没有变化，所以总带宽为O(mn2)。但每次只实时发送一个数据，因此增加了参与方之间的通信轮次，总通信轮次为O(n2)。

3.4.3 协议比较

本协议与现有安全多方乘积协议的性能比较，如表1所示。表中，l、p为茫然传输安全系数，n为参与方个数，m为数据长度。文献[11]提出多方矩阵乘积协议，当矩阵维数是1的时候就退化为数量乘积。假设在理想通信环境下，计算一个中间数据的时间为1。

由表1可知，本文利用同态加密技术，在保证安全性的同时，减少了数据量，避免了文献[10]和文献[11]中所有参与方两两之间都需要频繁通信的情况，降低了通信代价。在计算代价相当的情况下，协议1和协议2各有优势，串行协议通信轮次少，适用于通信较为复杂的网络环境；当网络环境较为理想或者参与方数量较多时，并行协议参与方无须等待，可以减少协议的执行时间。

此外，本文的通信模型为环形，此模型可进一步优化。根据参与方之间的通信代价，设计一个通信代价最低的环，提高协议执行效率；也可以结合信任评估模型[15]设计一个通信方之间信任度最高的环，提高协议的安全性。与文献[10]和文献[11]中的复杂网状模型相比，本文降低了对通信环境的要求，无需所有参与方之间都存在通信关系，只要能形成一个通信环，协议便能正确执行，减少了被攻击的途径。

4 结束语

安全多方计算在信息和通信安全中都占有重要的地位，而同态加密技术是安全多方计算中的关键技术之一。结合实际，本文提出了两个适用不同环境的安全多方乘积协议，协议无须第三方的参与，在保证安全性的同时降低了通信代价，提高了协议的执行效率。此外，现有的安全多方计算协议多为两方协议的扩展，本文提出一个SMC基础协议，为研究安全多方计算其他问题提供了新思路。本文是基于半诚实模型下的协议，恶意模型下参与方可能不完全遵守协议，如何对参与方的行为进行验证，构建安全的多方计算协议有待进一步研究。

[1]Yao A C.Protocols for secure computations[C]//Proceedings of the 23rd Annual IEEE Symposium on Foundations of Computer Science.Los Alamitos：IEEE Computer Society Press，1982：160-164.

[2]Goldreich O，Micali S，Wigderson A.How to play any mental game[C]//Proceedings of the 19th Annual ACM Conference on Theory of Computing，1987：218-229.

[3]刘文，罗守山，王永滨.安全两方向量优势统计协议及其应用[J].电子学报，2010，38（11）：2573-2577.

[4]秦静，张振峰，冯登国，等.一个特殊的安全双方计算协议[J].通信学报，2004，25（11）：35-42.

[5]Du Wenliang.A study of several specific secure two-party computation problems[D].West Lafayette：Purdue University，2001.

[6]肖倩，罗守山，陈萍，等.半诚实模型下安全多方排序问题的研究[J].电子学报，2008，36（4）：709-714.

[7]刘文，王永滨.安全多方信息比较相等协议及其应用[J].电子学报，2012，40（5）：871-876.

[8]Maurer U.Secure multi-party computation made simple[C]//Proceedings of the 3rd International Conference on Security in Communication Networks，2003：14-28.

[9]李禾，王述洋.关于除法的安全两方计算协议[J].计算机工程与应用，2010，46（6）：86-88.

[10]张华.陈智雄.肖国镇.一个基于签密技术的安全多方乘积协议[J].计算机科学，2005，32（2）：50-52.

[11]罗文俊，李祥.多方安全矩阵乘积协议及应用[J].计算机学报，2005，28（7）：1230-1235.

[12]Naor M，Pinkas B.Oblivious transfer with adaptive queries[C]//Advancesin Cryptology（CRYPTO’99）.Berlin Heidelberg：Springer-Verlag，1999.

[13]Paillier P.Public-key cryptosystems based on composite degreeresiduosity classes[C]//Advancesin Cryptology（EUROCRYPT’99）.Berlin Heidelberg：Springer-Verlag，1999：223-238.

[14]Goldreich O.Secure multi-party computation（manuscript Version1.3）[EB/OL].（2009-10-09）[2013-01-18].htttp：//www.wisdom.weizmann.ac.il/～oded/pp.html.

[15]Duma C，Shahmehri N，Caronni G.Dynamic trust metrics for peer-to-peer systems[C]//Proceedings of the 16th International Workshopon DatabaseandExpertSystems Applications.[S.l.]：IEEE，2005：776-781.