多跳多接口无线网络中的协作路由

谢 鲲，王 玲

湖南大学 信息科学与工程学院，长沙 410082

1 引言

协作通信技术利用单天线移动终端之间的相互协作，共享彼此的天线，形成虚拟的MIMO系统，从而获得空间分集效应。因其能够抵抗无线信道衰落，提升系统性能，成为近年来通信领域的研究热点之一。

现有的协作通信研究主要可以分为两类：一类是在单跳无线网络中的协作通信，主要研究在两个无线通信节点之间如何选择一个或者多个协作中继节点，进行资源的最优分配以获得最大性能。如文献[1-3]研究了单跳无线网络中协作中继节点选择和功率分配问题。另一类是在多跳无线网络中的协作通信，研究多跳网络中如何寻找协作路由来增加传输可靠性[4-5]，以及如何联合协作路由和协作中继选择提高网络传输容量等[6]。

在多接口无线网络中，可以为每一个无线节点配备多接口。现有的研究表明，相比于单接口网络，多接口网络可以提高传输性能和可靠性。然而，现有针对多接口无线网络中协作通信研究还十分有限，仅文献[7]考虑了多接口网络环境下协作传输问题。但是，文献[7]是在给定路由的情况下再进行接口的分配，无法动态为业务流进行路由选择，并不能为多条数据流提供最优的性能。

多接口协作网络可以为网络通信提供更多的资源，使得节点在发送的过程中能够有更大的空间来选择下一跳流量转发节点和协作节点。而且，在多接口协作无线网络中，节点的多个接口既可以服务某些数据流的直接传输，又可以为另外一些数据流提供协作通信服务。如何在多个数据流存在的情况下，合理地在多个数据流中进行接口分配，联合考虑路由和中继节点选择来最大化网络性能，成为多跳多接口协作无线网络实现的关键和难点。

为解决该问题，本文首先分析在新的网络场景下联合路由选择和中继分配的问题模型。根据网络场景建立各个约束条件，将本文中最大化最小数据流速率的路由选择和中继分配问题建模为一个混合整数线性规划问题。然后，提出分支定界（branch and bound）的联合路由选择和中继分配算法，该算法利用分支定界的思想将原问题分解为多个子问题来获得最优解。在具体实现中，将解空间用上下界来逼近，在算法迭代过程中更新上下界，当上下界之差小于某个给定的小数值时，当前的整数解集则为最优解，该最优解对应了最优的路由和中继节点分配情况。

2 网络模型与问题描述

2.1 三个节点的协作通信模型

协作通信技术是适合于单天线用户的空间分集技术，它利用无线信道的广播特性，允许单天线终端设备在多用户环境中共享它们的物理资源来进行通信，形成虚拟天线阵列。

参与协作通信的设备可相互转发信息，同一信息的多个复本能够通过相互独立的无线信道到达接收端。图1给出了协作通信的三节点通信模型，这里s是源节点，d是目标节点，r是协作中继节点。图1中的信源节点s和协作中继r形成相互独立的通信信道，这样信源节点发送的多个信号复本通过相互独立的信道到达接收端，便可产生分集增益。相比于传统的直接传输，协作通信可达到更高的吞吐量、更低的误码率并消耗更少的能量[8-9]。尽管三节点协作通信模型很简单，但是协作通信的具体实现机制却并不是唯一的。在文献[10]中，使用一种时隙模型来传输。然而由于正交信道模型比时隙模型更容易分析和处理，并很容易转为使用频率分集、时间分集或者码域分集，所以正交信道的使用已经在协作通信中被广泛接受[1，4，11-13]。类似于文献[6]的协作通信协议，本文也采用正交信道来研究协作通信。在多跳多接口网络环境中，每个节点使用单独的信道，并能够在不同信道中同时无自干扰地传输和发送数据。

图1 三节点协作通信模型

在协作传输模型中，根据中继转发节点处理信号机制的不同，有两种常用的通信模式：放大转发和解码转发。本文采取放大转发模式，下面给出在放大转发模式下源节点s和目的节点d之间可达速率计算公式。

如图1所示，中继节点r接收、放大并转发来自于源节点s的信号到目的节点d。hsd、hsr、hrd分别表示s和d，s和r，r和d之间的路径损耗、阴影和衰落等影响。zd和zr分表表示在节点d和r上的零均值，且方差分别为、。为了简便，假设一个节点的背景噪声在不同的信道上都有相同的随机特性。Ps和Pr分别表示在节点s和r处的传输功率。

根据文献[6]可知，放大转发模式下，在s和d之间由r作为协作中继的情况下可达到的速率为：

如果源节点和目标节点采用直接传输方式，即源节点s直接发送数据到目的节点d，则可达速率为：

CD(s，d)=wlb(1+SNRsd)

2.2 数学模型

2.2.1 网络场景和定义

本文考虑存在多条数据流的多跳多接口协作无线网络，如图2所示，每个节点配备两个网卡，每个网卡使用单独的信道收发信息，且每个节点可以同时为两条流服务。

图2 网络场景说明图

网络中有n个节点，记为集合N；网络中J条流，记为集合F={f1，f2，…，fJ}。那么节点集合N包含三部分：（1）J个源节点，记为集合Ns={s1，s2，…，sJ}；（2）J个目的节点，记为集合Nd={d1，d2，…，dJ}；（3）L个中间节点，记为集合Nr={r1，r2，…，rL}。因此有n=J+J+L=2J+L。

根据中间节点在数据流传输中的作用，可以分为两类。一类是多跳传输中继（Multi-hop Relay，MR），与传统路由中多跳转发节点功能相同，本文中的MR传输中继作为多跳路由的转发节点来转发数据包（如图2中为f1服务的r2、r5、r7和为f2服务的r1、r4、r6和r7），下面定义0-1变量T(i，u，v)来形式化表示多跳传输中继MR：

这里节点u和v都是流fi中的MR。

另一类用于节点之间的协作转发，即帮助源节点传输数据给目的节点的协作者，称为协作传输中继（Cooperative Relay，CR）（如图2中为f1服务的r3和r6和为f2服务的r2和r3），发送节点、接收节点和协作传输中继共同组成如图1所示的协作传输模块。这里同样定义0-1变量G(i，u，w，v)来表示协作传输中继CR：

这里，节点u和v仍为fi的MR，节点w为CR。

2.2.2 问题的描述和建模

首先根据网络中各个节点为网络数据流服务和中继转发的功能出发，分析网络中各个节点在联合路由选择和中继分配问题中的约束条件。

（1）源节点：每条流是从相应的源节点出发，所以源节点必有流出，即

文中假设源节点和目的节点不能作为MR，即除了作为初始节点或者目的节点之外，若为其他流服务只能作为中继转发节点，也就是CR，所以有：

（2）目的节点：目的作为本条流的终止节点，其一定有流入，即

类似于源节点，目的节点为其他流做中继转发节点，也最多只能为一条流服务，即：

（3）中间节点：

①作为MR，一个中间节点u作为MR为某条流fi服务，则必有流入和流出，所以中间节点u在fi这条流中下一跳之和应该满足

上一跳之和应该满足

由于流入和流出是同时存在，所以

②作为CR，为某条流fi服务的另一种方式就是作为协作中继CR，但是也只能为其中的某一跳作为中继，则有：

而且中间节点u为fi这条流服务的时候就只能作为MR或者CR，二者只能取其一，则有：

然后就整个网络来说，由于假设源节点和目的节点为其他流服务时不作为MR，所以源节点是没有流入的，目的节点是没有流出的，即：

就整个网络来讲，某个中间节点u最多只能为两条流服务，也就是：两个MR或者两个CR；一个MR一个CR；一个MR或者一个CR。不参与网络服务，所以有：

若网络中某条流fi中流经(u，v)，若w为(u，v)的中继转发节点应满足：

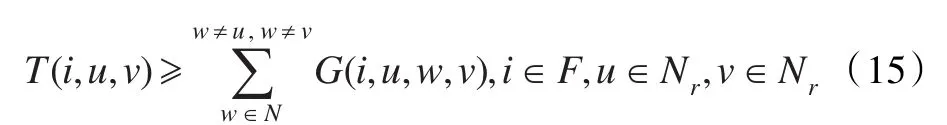
假设每条流的速率为ci，那么为了确保路由的可用性，就必须考虑网络中每一跳的容量限制，所以对fi的每一跳(u，v)都有：

2.2.3 问题的形式化描述

网络中有n个节点，J条数据流，本文的目标是通过优化多条流路由和协作中继分配来最大化最小的数据流的速率。若Cmin表示这J条流中最小的流速，即Cmin=min{c1，c2，…，cJ}，那么本文目标就是最大化Cmin。

条件（16）是由两个变量相乘的非线性限制约束条件。为了简便求解，需要将该非线性约束转化成一个线性约束：

根据式（15）可知，当T′=0的时候，G′=0，所以G′T′=G′，当T′=1的时候，G′T′=G′，因此式（16）还可以简化为：

在上述条件中，式（5）、（7）等价于式（5）、（6）、（7），因此可以忽略条件（6）；式（7）、（9）等价于式（7）、（9）、（10），因此也可以忽略条件（10）。

本文的最大化最小数据流的联合路由选择和中继分配问题可以形式化表示如下：

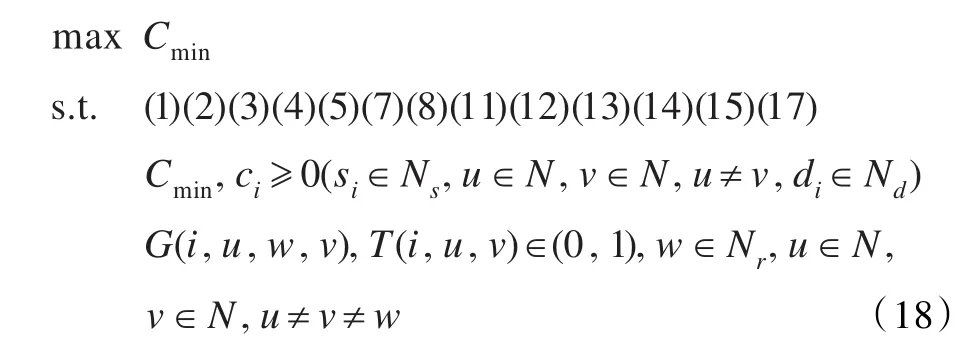
分析可知式（18）是一个混合整数线性规划问题（MILP），所有的约束条件都是线性约束，Cmin是目标函数，T(i，u，v)和G(i，u，w，v)是决策变量，一旦所有数据流的T变量和G变量确定后，路由选择和中继分配即可确定。通常来说MILP问题是一个NP-hard问题[14-15]。为了求解该问题，本文提出一种启发式算法。

3 基于分支定界的联合流路由和中继节点分配算法JFRBB

分支定界法（Branch and Bound）是一种系统地搜索解空间的方法，它隐式地将所有决策变量组合的解都求出来然后取最优值。通过定界直接删除一些目标函数值明显低于当前最优值的某些变量值，不再对其分支，从而减少搜索空间，减少空间复杂度，提高算法效率。因此，分支定界法求出的解通常为优化问题的最优解。

本文基于分支定界思想的联合流路由和中继节点分配算法具体步骤，如图3所示。

图3 基于分支定界思想的联合流路由和中继节点分配算法

如对于一个求最大值的混合整数线性优化问题（18），表示为P，其决策变量（0-1变量）集合为X，分支定界第一步就是先忽略决策变量的整数限制，得到一个非整数解集X0和目标函数值UB0。

然后选择P的任意整数可行解集X00（如所有变量都取0）代入P得到另一个目标函数值LB0。这时取P得最优目标函数值的上界UB=UB0，下界LB=LB0，用一个整数解集Y=X00，如图4（a）所示。

接下来从这个非整数解集X0中找出任意一个非整数变量x1开始分支成两个子问题，P1：x1=0和P2：x1=1。分别对P1和P2进行求松弛解，过程同第一步，则对于P1，可以得到一个非整数解集X1和目标函数值UB1，以及一个整数解集X11和目标函数值LB1。同样对于P2，也可以得到一个非整数解集X2和对应的目标函数值UB2，以及一个整数解集X22和对应的目标函数值LB2，如图4中（b）所示。

（1）如果LB1＜LB，LB2＞LB，表明P1这个分支得到的整数解没有当前整数解好，则删除P1这个子问题，就是不再对其进行分支，并取UB=UB2，LB=LB2，Y=X22，判断是否满足UB≤(1+ε)LB（ε＞0，是一个给定的误差值），如果上述不等式成立，则分支定界算法结束，LB对应的整数解集Y则为要求的决策变量解集，LB则为目标函数值；否则就从非整数解集X2中再任取一个非整数变量xi分支成两个新的子问题继续求解，过程同上述分支一样。

图4 分支定界步骤

（2）同理如果LB2＜LB，LB1＞LB，表明P2这个分支得到的整数解没有当前整数解好，则删除P2这个子问题，即不再对其进行分支，并取UB=max{UB，UB1}，LB=LB1，Y=X11，同上面一样判断是否满足UB≤(1+ε)LB，如果上述不等式成立，则分支定界算法结束，LB对应的整数解集Y则为要求的决策变量解集，LB则为目标函数值；否则就从非整数解集X1中再任取一个非整数变量xi分支成两个新的子问题继续求解。

（3）如果LB1＞LB，LB2＞LB，表明分支后两个子问题所得到的整数解都优于当前整数解，则取UB=max{UB1，UB2}，LB=max{LB1，LB2} ，同样判断是否满足UB≤(1+ε)LB，如果上述不等式成立，则分支定界算法结束，LB对应的整数解集Y则为要求的决策变量解集，LB则为目标函数值；否则就依次从非整数解集X1和非整数解集X2中任取一个非整数变量来分支成两个新的子问题继续求解，如图4（c）所示为子问题P2的分支。

（4）如果LB1＜LB，LB2＜LB，表明有当前的整数解优于两个分支所得的整数解，因此对这两个问题都不在分支。

上述过程结束后的分支求解类似于P问题的分支过程，算法结束的标志都为上UB≤(1+e)LB或者所有分支灰没有可行解，LB对应的整数解集为当前的最优解集，LB为目标函数值。

4 仿真实验

4.1 实验设置

本文通过仿真实验来验证提出的联合优化路由和中继节点算法的有效性。

在仿真实验中，沿用文献[12]的参数设置，假设每个接口带宽W=22 MHz，每个节点的最大传输功率设为1 W。为了方便计算，假设hsd只包含节点s到d的传播增益，所以|hsd|2=||s-d||-4，这里||s-d||是节点s和d之间的距离，路径损耗参数设为4，给定的误差值ε=0.1；并假设所有节点噪音的方差为10-10W。

图5 JFRBB-Multi-Radio-Cooperative路由

网络拓扑如图5所示，在大小为1 000 m×1 000 m的范围内随机生成16个节点。其中4个源节点，4个目的节点，8个中继节点，也就是n=16，J=4，L=8。图中实线表示节点之间存在直接通信的链路，虚线箭头表示协作通信链路。目前多接口协作无线网络中的研究还十分有限，因此本文对比三种不同的网络场景和路由算法来分析本文所提算法的性能。

第一种在双接口协作网络中，实现本文提出的JFRBB算法，即为每个数据流找到协作路由的同时确定每个接口中继分配情况（即MR和CR分配情况），表示为JFRBB-Multi-Radio-Cooperative。

第二种在双接口无协作传输的网络中为每条数据流利用JFRBB算法找出最优路由，表示为JFRBB-Multi-Radio-Noncooperative。在这个场景中，由于没有协作节点协作转发，因此，每个节点的两个接口最多只能同时作为MR为两条流服务。由于没有了协作节点转发，具体实现中，将JFRBB算法中所有的G变量赋值为0，此时的决策变量只有T。

第三种在单接口协作网络中，利用 JFRBB算法为每个数据流找出最优的协作路由，并进行中继分配，表示为JFRBB-Single-Radio-Cooperative。由于网络场景为单接口网络，每个节点只有一个接口，因此每个节点只能作为MR或者CR为某一条流服务。具体实现中将JFRBB算法所有的接口数目限制设为1，即在问题（19）的数学模型中，约束条件（13）、（14）的接口数目限制改为1。

4.2 实验结果

图5给出了JFRBB-Multi-Radio-Cooperative网络中的路由结果，图6和图7分别为JFRBB-Multi-Radio-Noncooperative网络路由情况和JFRBB-Single-Radio-Cooperative网络的路由情况。网络中各条流的速率如表1所示，可以看出在JFRBB-Multi-radio-cooperative网络路由中，由于每个节点可以为多条流服务，节点既可以作为MR又可以作为CR，所以由此算法得到的网络性能是最好的。而在JFRBB-Multi-Radio-Noncooperativ网络中，虽然每个节点也是多个接口，但是网络节点只能作为MR，没有了协作分集的优势，网络中各条流的速率比JFRBB-Multi-Radio-Cooperative路由的速率要小。在JFRBB-Single-Radio-Cooperative网络中，虽然有协作节点的转发，但是网络中各个节点只有一个接口，只能服务于一条流，使得有些有优势的节点得不到充分的利用，从而降低了网络性能。

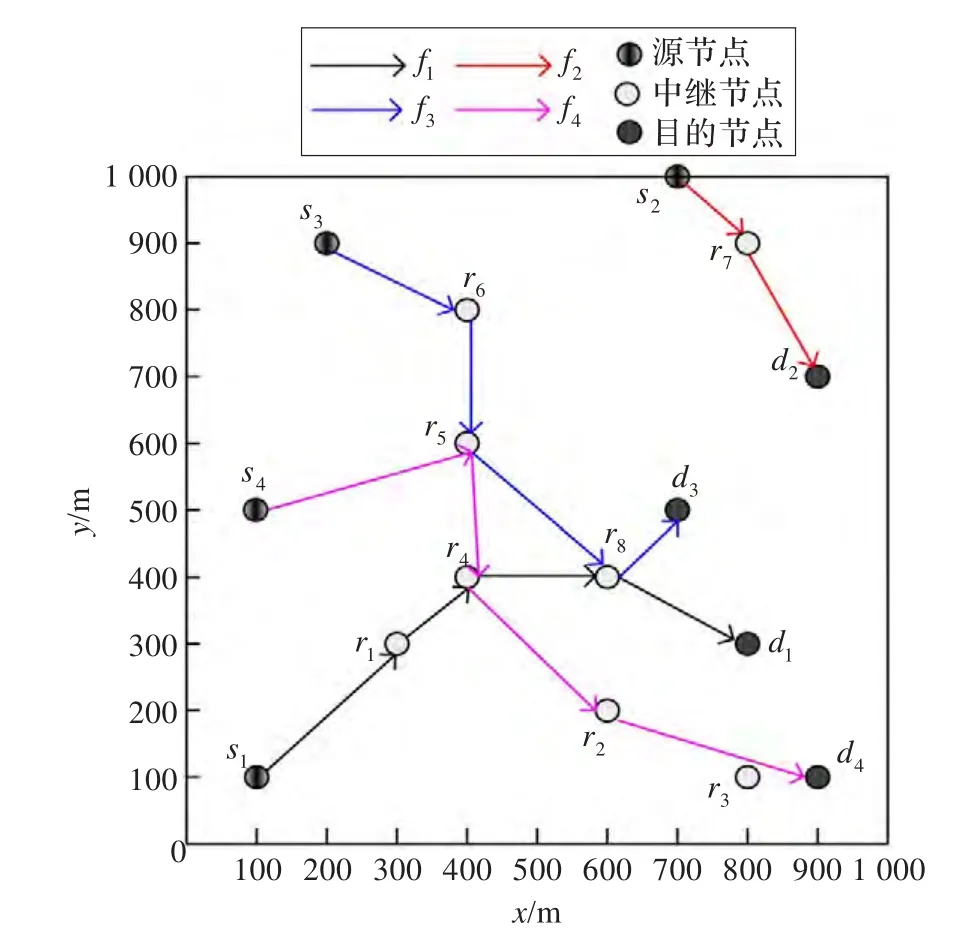
图6 JFRBB-Multi-Radio-Noncooperative路由

表1 网络中各条数据流速率比较 （Mb·s－1）

图8给出了三种情况下各个网络中的最小速率，可以看出JFRBB-Multi-Radio-Cooperative路由的最小速率比JFRBB-Multi-Radio-Noncooperative和JFRBB-Single-Radio-Cooperative网络的最小速率均高出将近43%。图9给出了各个网络中的聚合流量，由图可以看出，在JFRBB-Multi-Radio-Cooperative路由情况下聚合流量比JFRBB-Multi-Radio-Noncooperative网络和JFRBB-Single-Radio-Cooperative网络的聚合流量分别高出16.4%和30.7%。

上述实验结果表明，一方面，由于协作通信带来的协作分集效应，协作通信可以进一步提高多接口无线网络的性能；另一方面，多接口为协作传输的MR和CR分配带来了多样性的选择，可以为协作通信服务，进一步提高网络性能。

图9 网络中聚合流量比较

5 总结

协作通信可以充分利用网络中的节点资源，通过节点间的协作来帮助有通信需求的节点进行高速、可靠的无线通信。本文在多接口多跳网络中，联合流路由和中继节点选择，为各条数据流寻求一条最优路径，使得各条流之间以较为均衡的速率传输数据。由于多接口能够使一个节点服务于多条流，所以多接口网络中的节点更能充分地发挥自己的优势，来最大限度提高网络吞吐量。仿真实验结果表明，基于分支定界的联合流路由和中继节点分配算法能够提高网络传输速率，并公平实现各条数据流的带宽分配。

[1]Cai J，Shen S，Mark J W，et al.Semi-distributed user relaying algorithm for amplify-and-forward wireless relay networks[J].IEEE Transactions on Wireless Communications，2008，7（4）：1348-1357.

[2]Shi Y，Sharma S，Hou Y T，et al.Optimal relay assignment for cooperative communications[C]//Proceeding of ACM MobiHoc，Hongkong，China，May 27-30，2008：3-12.

[3]Zhao Y，Adve R，Lim T J.Improving amplify-and-forward relay networks：optimal power allocation versus selection[C]//Proc IEEE International Symposium on Information Theory，Seattle，USA，July 9-14，2006：1234-1238.

[4]Scaglione A，Goeckel D L，Laneman J N.Cooperative communications in mobile ad hoc networks[J].IEEE Signal Processing Magazine，2006，23（5）：18-29.

[5]Yeh E M，Berry R A.Throughput optimal control of cooperative relay networks[J].IEEE Transactions on Information Theory，2007，53（10）：3827-3833.

[6]Sharma S，Shi Y，Hou Y T，et al.Cooperative communications in multi-hop wireless networks：joint flow routing and relay node assignment[C]//Proc of IEEE Infocom 10，2010.

[7]Li Xiaoguang，Wu Jie.Channel on demand：optimal capacity for cooperative multi-channel multi-interface wireless mesh networks[C]//Proceedings of the Conference on Mobile Adhoc and Sensor Systems（MASS），2010：412-421.

[8]Khandani A E，Abounadi J，Modiano E，et al.Cooperative routing in static wireless networks[J].IEEE Transactions on Communications，2007，55（11）：2185-2192.

[9]Li F，Wu K，Lippman A.Energy-efficient cooperative routing in multi-hop wireless ad hoc networks[C]//Proc of the 25th IEEE International Performance，Computing，and Communications Conference，April 10-12，2006：215-222.

[10]Laneman J N，Tse D N C，Wornell G W.Cooperative diversity in wireless networks：efficient protocols and outage behavior[J].IEEE Transactions on Information Theory，2004，50（12）：3062-3080.

[11]Gurewitz O，de Baynast A，Knightly E W.Cooperative strategies and achievable rate for tree networks with optimal spatial reuse[J].IEEE Transactions on Information Theory，2007，53（10）：3596-3614.

[12]Hunter T E，Nosratinia A.Diversity through coded cooperation[J].IEEE TransactionsonWirelessCommunications，2006，5（2）：283-289.

[13]Savazzi S，Spagnolini U.Energy aware power allocation strategies for multi-hop cooperative transmission schemes[J].IEEE Journal on Selected Areas in Communications，2007，25（2）：318-327.

[14]Garey M R，Johnson D S.Computers and intractability：a guide to the theory of NP-completeness[M].New York：WH Freeman and Company，1979.

[15]Pochet W L A.Production planning by mixed integer programming[M].Now York：Springer-Verlag，2006.