电动汽车电池更换站集群充电控制策略研究

张齐东 黄学良 陈 中 陈立兴 徐云鹏

电动汽车电池更换站集群充电控制策略研究

张齐东 黄学良 陈 中 陈立兴 徐云鹏

（东南大学电气工程学院 南京 210096）

本文基于规模化电动汽车充放电负荷模型，建立考虑车主互动意愿的电价模型，通过电价对车主的换电池行为进行有序引导，从而实现电网的调峰策略。采用遗传算法对适用于电动汽车的最优日前实时电价进行求解。最后建立电动汽车电池更换站内集群充电的控制模型，以电池更换站的运行经济性与站内充放电机状态切换次数最优为目标，采用智能算法对集群调度模型进行求解，实现在满足用户换电池需求基础之上的换电站最优化运行。

电动汽车 智能电网 换电站 有序充电 调度策略

1 引言

根据国务院通过的《节能与新能源汽车产业发展规划（2012—2020年）》统计，到2015年，我国纯电动汽车和插电式混合动力汽车累计产销量达到50万辆，到2020年将会超过500万辆，专家预计2030年将会超过3000万辆。据统计2013年全国纯电动汽车保有量为38.16万辆。据派克研究所的一份最新报告显示，中国电动汽车每年的复合增长率则预计会超过40%，由这一预测可知，到2020年我国纯电动汽车保有量将达到402.25万辆，到2030年将达到1372.11万辆。电动汽车规模化发展是必然趋势。

规模化电动汽车的接入对电网的安全运行将是一个巨大挑战,为此国内外众多学者研究了电动汽车接入电网后对配网的影响[1-3]，包括电动汽车充电负荷的分布与预测[4-6]以及电动汽车充电调度的实现方法[7,8]。在电动汽车充电站内运行策略的优化方面，文献[9]研究了换电模式下不同时段的充电需求，得到了应该储备的电池组数量；文献[10]研究了基于动态电价的充电决定策略，并建立了购买电池原始投资和后期运营成本的经济数学模型；文献[11]测试和分析了充电站的不同运营模式；文献[12]以降低网损为目标，对电动乘用车的有序充电进行了研究。现有研究多以快速充电或者慢速充电这类单一充电方式为研究对象，且在优化过程中并未考虑电池自身的寿命折损因素。本文重点基于电动汽车的换电池模式在互动方面的优势性，在电网采取实时电价的条件下，对站内电池组的充放电控制策略进行了仿真，以电池更换站收益最大与站以及站内充电桩与电池健康度最大为目标进行了优化设计，即保证了运营经济性，又最大程度的降低了反复充放电过程给电池带来的损伤。

2 基于电网调峰策略的实时电价模型

2.1电池更换站网络实时电价计算模型

电动汽车作为一个能量存储库，V2G技术可以实现电动汽车和电网的能量双向流动[13,14]，其充电行为还可以通过制定峰谷电价或者实时电价等手段进行控制，受到了广泛的关注和研究[15]。实时电价即实时定价。在用电高峰时段，将电价调高，而在用电低谷阶段，将电价降低，从而使电动汽车用户有选择地避开用电高峰时期，实现电网峰谷调节的需求。

研究表明，除了公交车等特殊车辆，一天中超过90%的时间里汽车会处于停驶状态[16]。理论上认为所有停驶的电动汽车均可以参与V2G。

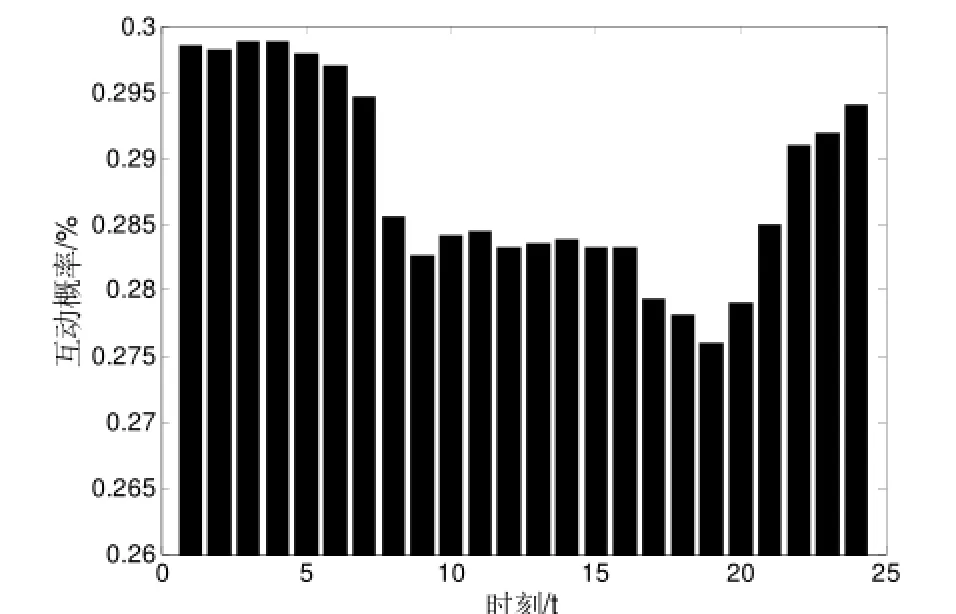
图1 电动汽车互动概率Fig.1 Interaction probability of electrical vehicles

但是，并不是所有停驶电动汽车的车主都愿意参与V2G，因此还需要考虑车主的互动意愿，则在时段t可以调度的电动汽车数量Ndis(t)为:

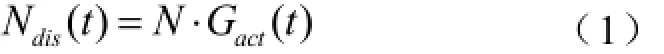
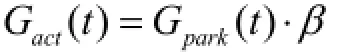
其中，式中，N为区域电网中电动汽车的数量；Gpark(t)为电动汽车的停驶概率；β为互动意愿率，即愿意参与V2G的车主占所有车主的比例。

电动汽车互动概率Gact(t)随时间的变化情况如图1所示。

2.2日前电价求解

所建立的电价模型旨在调度愿意互动的电动汽车，一方面满足车主的充电要求，另一方面实现削峰填谷，优化电网运行。

（1）目标函数

优化目标为电网等效负荷方差最小为:

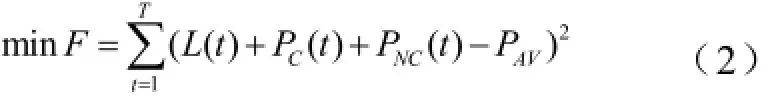
其中，

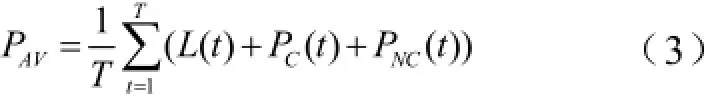
式中，t∈1，2，…，T；T为研究周期内的小时数，本文中取24，即研究日实时电价；L(t)为时段t的常规负荷值；PC(t)为时段t愿意参与V2G的电动汽车充电功率；PNC(t)为时段t不愿意参与V2G的电动汽车充电功率。

（2）约束条件

约束条件应包括确保所有愿意参与V2G的电动汽车在一个调度周期内总的充电功率保持不变，即充电量等于用电量，以及对充电功率的约束，表示如下:

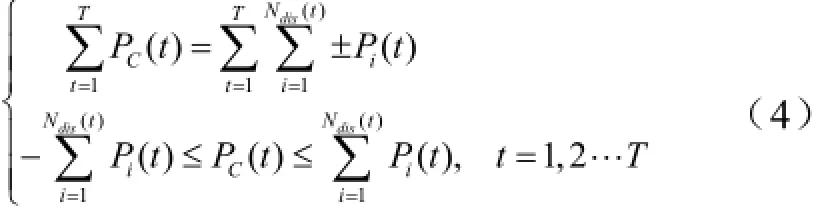
式中，Pi(t)为第i辆电动汽车在时段t的充电功率，Pi(t)＞0表示充电，Pi(t)＜0表示放电。

一般情况下，在用电高峰时段，将电价调高，鼓励用户放电；而在用电低谷阶段，将电价降低，鼓励用户充电，从而可以达到以电价引导电动汽车充放电来实现移峰填谷的目的。对于由电价升降所引发用电量的变化即弹性系数ε，其计算公式如下所示[17]:

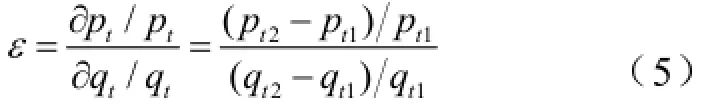
式中，qt1和qt2分别表示时段t的参考电价和当前电价；pt1和pt2分别表示时段t的参考负荷值和当前负荷值。

2.3 当日电价求解

本文考虑在某一个时间窗口内，通过优化电动汽车的充电功率来补偿日前预测值与时前预测值之差，使预测误差与电动汽车充电功率变化量之和的绝对值最小，并且使该时间窗口内电动汽车总的充电功率保持不变。

（1）目标函数为:其中，

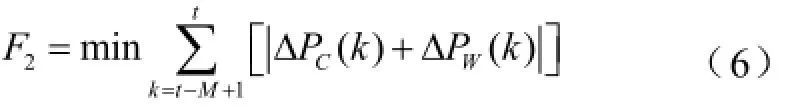
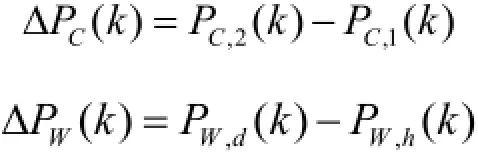
式中，M为时间窗口的时段数；PC,2(k)为第二次优化中，时段k愿意参与互动调度的电动汽车的充电功率；PW,h(k)为时段k风电功率的时前预测值。

（2）约束条件

约束条件与计算日前电价时的约束条件相同为:

式中，t可在M，M+1，…，T中取值。

3 电动汽车电池更换站内集群充电控制策略

换电池为电动汽车能量补充的重要方式，能够缩短用户的等待时间，且换下的电池由电池更换站统一进行充电，方便调度管理，将成为未来电动汽车能量补给的重要方式之一。本文以选取优化最小时间单位为半小时，优化时段为24h，根据次日的进站流量密度曲线对电池更换需求进行预测，对次日的电池更换站充换电流程进行优化。认为用户换给充电站的电池均已使用至电量阀值（剩余20%）。按照电池的健康程度，将站内的电池按一定比例分为A、B、C三组，针对不同的健康程度设定不同的使用方案。在此之外需要额外考虑一部分的备用电池，这部分备用不参与放电收益，仅作为换电备用使用。

3.1目标函数

A．电池更换站全天运行收益最大

以电池更换站向用户提供电池更换服务的收益与向电网馈电所得的收益总和最大为目标，目标函数为:

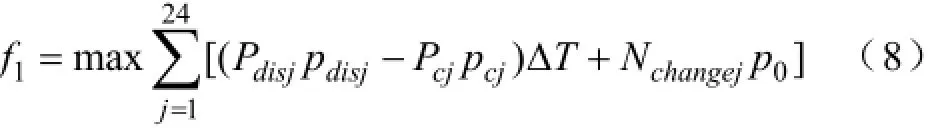
式中Pdisj、Pcj分别为j时段电池更换站内的馈电总功率和充电总功率；pdisj、pcj分别为j时段电池更换站向电网馈电的电价和从电网买电的电价，p0为电池更换站换给用户一块电池所收取的费用，为固定常数；Nchangej为j时段换给用户的电池数目；△T为单位优化时段。

B．电池更换站内充放电机及电池健康度最优

以电池更换站内充放电机在一天之内状态切换次数总和最小为目标，目标函数为:式中nswitch为站内所有电池组1d之内状态切换总次数；充放电机状态切换次数是由变量矩阵统计所得。

3.2约束条件

A．站内电池总数的约束

电池更换站内可供使用的各组别电池数量应小于等于各组别已充满电池的数量与备用电池数之和；且A、B、C三组电池在各个状态下的数量综合应等于该站拥有的电池数。

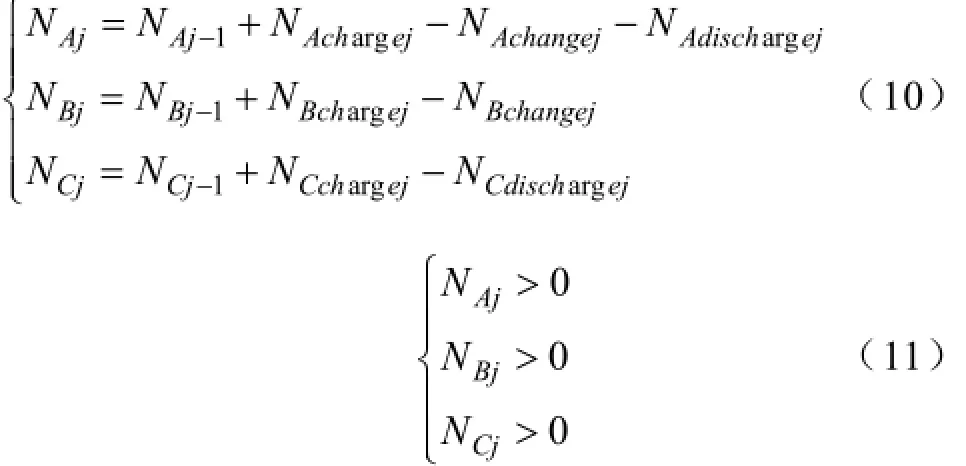
式中，NAj、 NBj、 NCj分别为从初始时刻到j时刻这段时间内，A、B、C三组电池中处于已充好状态的电池数量。

NAchargej、 NBchargej、 NCchargej分别为当前j时段A、B、C三组电池中已充好的电池数量。

NAchangej、 NBchangej分别为当前j时段A、B两组电池中可以提供给换给用户更换的数目，由于C组电池不参与电池更换，因此不存在 NCchangej。

NAdischargej、 NCdischargej分别为当前j时段A、C两组电池中处于放电状态的电池数量，由于B组电池不参与并网放电，因此不存在 NBdischargej。

B．充放电机数目约束

当前j时段所有处于充电、放电状态的电池总数应不超过站内充电机数量M，约束条件表达式为:

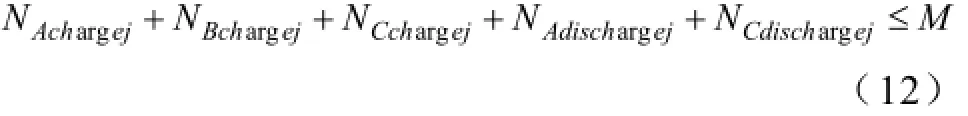
C．用户需求约束

站内可用于用户更换的电池数量满足当前车辆换电量，并保证20%的裕度。

D．连续充电约束

设定电池完成一次充电行为需要的时间为Δt，电池接入某一充放电机时，该充放电机的持续工作时间应为Δt的整数倍，即保证充放电机工作状态的连续性，避免出现频繁的充放电状态切换。

3.3变量设置

在每日24点之前，对电池更换站内的信息进行统计，以进行下一次日前计划的制定。包括站内所有充电机的工作状态、站内所有充电机的故障情况、站内所剩电池的信息。

每个充电机存在3种状态:充电、放电、和停运，对应实数[1，-1，0]。认为电机的充放电过程均为恒功率，效率均为90%。采取快充模式进行充电。设站内的充电机总数为M，对应于电池组的分类，同样也将充电机按电池组比例分为A、B、C三组，A组充电机仅对A组电池进行充放电操作，B、C组同理。那么变量矩阵表示为:

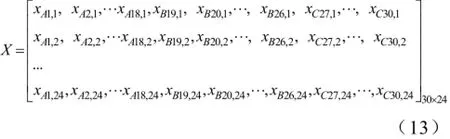
3.4优化算法

自适应改进行为人工鱼群算法的自适应性，体现在算法寻优程序在执行过程中重要参数的自动修正上[18]。改进方式如下:在算法的初始阶段，每条人工鱼在较大的可视域visual内以较大的移动步长step寻找较优解，从而扩大了算法的搜索范围。随着算法的迭代，自适应地减小可视域visual和移动步长step，从而自动的加快算法的收敛速度和有效地提高算法的求解精度。具体实现方式见式(14):

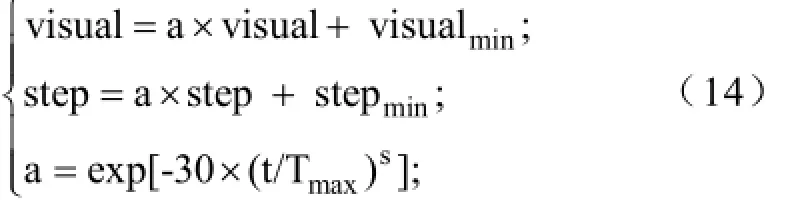
式中，visualmin为可视域最小值，取0.001；stepmin为移动步长最小值，取0.0002；Tmax为最大迭代次数；step为移动步长step = 0.125visual；α为衰减因子；t为当前迭代次数；s取值范围为[1 ,30]。Visual为可视域，其初值可以取搜索范围的最大值的1/4左右。式(14)对可视域visual 和步长 step 进行了改进；这种对参数进行自动修正的功能正解决了基本人工鱼群算法求解精度不高的问题。

电池更换站的充电策略优化属于带约束的优化问题，自适应改进行为人工鱼群算法直接可以用于无约束的优化问题中，而不可以直接用于带约束的优化问题中。惩罚函数法是一种可以把约束优化问题转化为一系列无约束优化问题来进行处理的方法[19]。如给定一带约束式子:

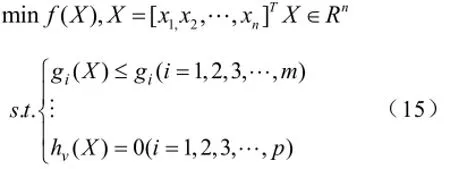
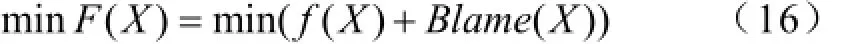
式中，f(X)为目标函数；Blame(X)为惩罚函数，将约束的条件表示成函数的形式；

根据惩罚函数法的性质，不难得到，对于求解最小值的目标函数f(X)来说，满足约束条件的X，均可以使Blame(X)的值为零。因此求解式(16)就相当于求解式(15)。

3.5仿真过程

电动汽车电池更换站内集群优化充电过程如图所示。

将带约束式子(4)转写成罚函数的形式:

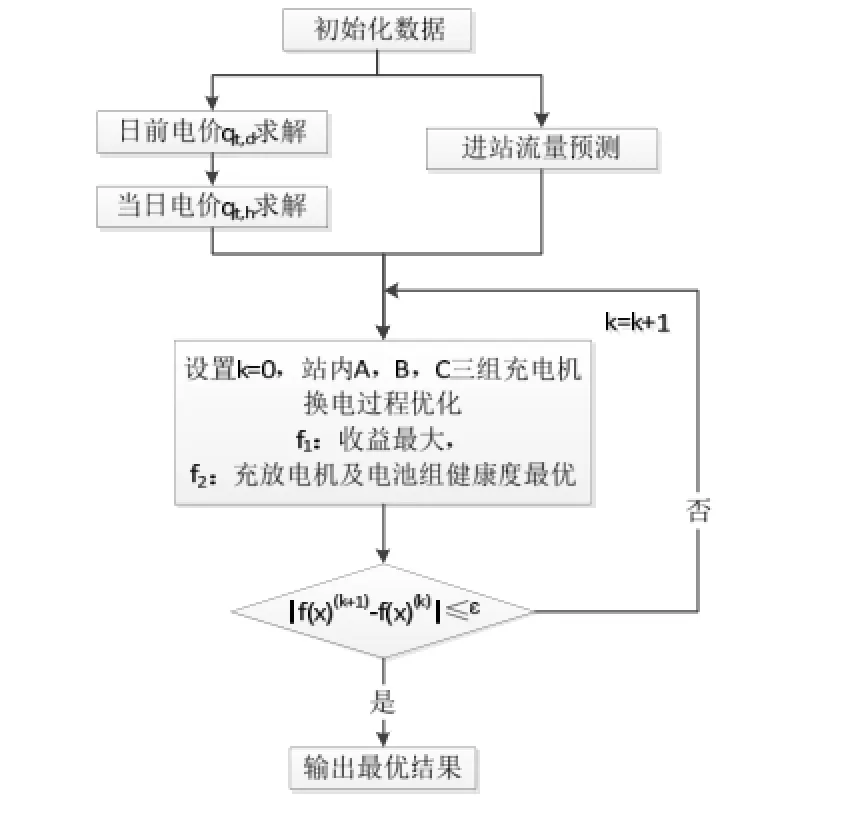
图2 电池更换站内最优充电策略求解电流程图Fig.2 The flow chart for solving the replacement battery charging station optimal strategies

首先将电动汽车用户通过互动意愿概率分为两类，以电网等效负荷方差最小为目标，通过弹性系数矩阵得到日前电价qt,d；其次通过优化电动汽车的充电功率来补偿日前预测值与时前预测值之差，得到当日电价qt,h；然后结合进站流量的预测，以收益最大和健康度最优分别对站内A、B、C三组充电机的换电过程利用人工鱼群算法进行优化，直至满足终止条件输出最优结果。

4 算例分析

根据实时电价与车辆流量的日前预测值，结合历史数据，通过模拟仿真计算，得到次日的的日前充电计划的充电机状态矩阵。输入信息如图3与图4所示。完成全天24h的换电工作模拟后，可以对电池更换站的收益进行统计分析。

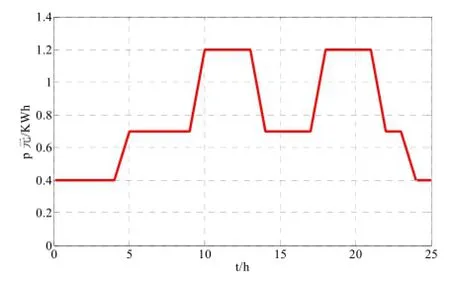
图3 充电价格预测曲线Fig.3 Price forecasting curve of batteries’ charging

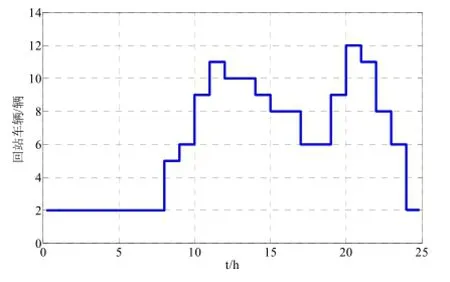
图4 未来24小时电池更换需求量预测曲线Fig.4 The battery replacement demand predict curve in the next 24 hours

对于电池更换站的换电池收费与馈电电价的计算思路如下:

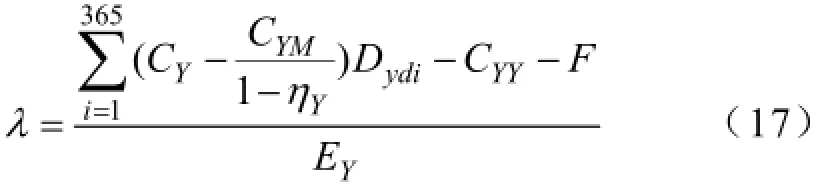
电池更换站年收益率为:式中，Dydi为电池更换站每天换电服务的所有电动汽车充电量；ηY为电池更换站充电损耗率；CY为电池更换站销售电价；CYY为电池更换站每年运营折算成本；CYM为电池更换站向电网购电电价，即充电成本价；EY为电池更换站建设成本；F为电池更换站每年租赁电池成本。

换一块电池的价格为CY*Q*0.8，其中Q为单块电池的容量；放电价格高于换电价格CY，取裕度10-20%。考虑到电池更换站的建设成本、电池购买成本、运行维护成本等问题，将馈电价格设为购电价格的5倍。

对电池更换站全天的收益与站内充电机的状态切换次数进行统计，得到图5与图6。从图中可以看出，充电机状态切换次数过多时，电池更换站的收益较低；当充电机状态切换次数低于某一数值时，其切换次数多少不再对电池更换站的收益产生规律性影响，此时电池更换站的收益仅收到充电成本、馈电收益、换电收益及电池备用率的影响。

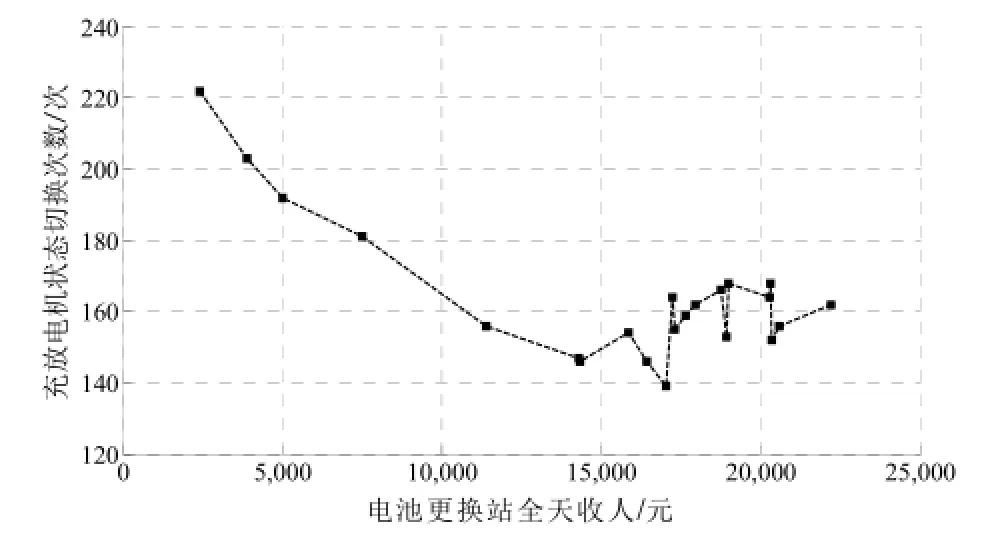
图5 电池更换站全天收入仿真结果Fig.5 The daily income of the battery changing station

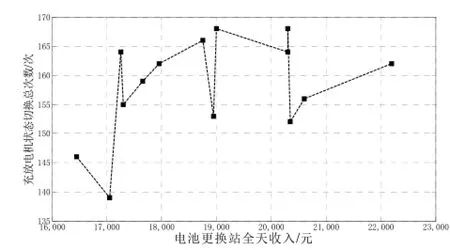
图6 充放电机切换次数低于180次时电池更换站全天收入仿真结果Fig.6 The daily income of the battery changing station based on the charge and discharge machines’ switching times below 180

通过计算得到，若不对站内电池的使用策略进行优化，仅按照用户的需求进行随用随充的充电安排，则无法使用空闲电池向电网进行馈电。按照这种方式进行经营，在不扣除电池购买成本、电池更换站建造及维护成本的情况下，整个电池更换站运行一天的收入约为1万元。

若考虑电池的优化分配，进行分类梯度利用，并对电池的充电时间进行优化，利用电池的空闲时段进行馈电，则在同等条件下，整个电池更换站运行一天的收入仿真结果如图5所示，当电池更换站内所有充放电机状态切换次数高于180次时，切换次数与全站的收入之间存在一定的反比关系，而当切换次数降到180次以下时，收入与充放电机状态切换次数之间就不再具有明显的比例关系，如图6所以，电池更换站的全天收入基本约在2万元左右。从图6可以得到优化结果，当站内所有电池的切换次数总和在162次时，电池更换站收益达到最大值22200元。

5 结论

本文主要研究充放电机的集群控制调度算法，以电池更换站的运行经济性与站内充放电机状态切换次数最优为目标，结合电池更换的管理策略与电池的梯度利用原则进行优化模型的设计，采用智能算法对集群调度模型进行求解，在满足用户换电池需求的基础之上实现自身运行的最优化。

通过算例仿真可以看出，电池更换站通过响应电网下发的不同电价实现自身的经济性最优，同时间接实现对电网调峰策略的响应；在此基础上以电池健康度为指标，通过梯度利用在保证电池健康的基础上进行电池的合理利用，最大限度地保证了站内电池的健康度，延长电池的使用寿命；并且约束条件中考虑了分时段用户满意度，实现全局总体优化。在切换次数降低到一定程度后可以得到最优可行解。

[1] C. N. kristien, H. Edwin, D. Johan. The impact of charging plug-in hybrid electric vehicles on a residential distribution grid[J]. IEEE Trans. Power System, 2010(25)： 371-380.

[2] W Su, M. Y. Chow. Performance evaluation of an EDA-based Large-scale plug-in hybrid electric vehicle charging algorithm[J]. IEEE Trans. Smart Grid, 2011, 3： 308-315.

[3] J. B. Ricardo, A. M. Manuel, J. S. Filipe, et al. Optimized Bidding of a EV aggregation agent in the electricity market[J]. IEEE Trans. Smart Grid, 2012, 3：443-452.

[4] 田文奇, 和敬涵, 姜久春, 等. 电动汽车充电负荷空间分配优化算法[J]. 电工技术学报, 2013, 28(3)：269-276.

Tian Wenqi, He Jinghan, Jiang Jiuchun, et al. Electric vehicle charging load spatial allocation optimization algorithm[J]. Transactions of China Electrotechnical Society, 2013, 28(3)： 269-276.

[5] 杨冰, 王丽芳, 廖承林. 大规模电动汽车充电需求及影响因素[J]. 电工技术学报, 2013, 28(2)： 22-27.

Yang Bing, Wang Lifang, Liao Chenglin. Research on Power-Charging Demand of Large-Scale Electric Vehicles and Its Impacting Factors[J]. Transactions Of China Electrotechnical Society, 2013, 28(2)：22-27.

[6] 徐国钧, 刘永胜, 李题印, 等. 基于层次分析和概率模拟的电动汽车对配网负荷影响研究[J]. 电力系统保护与控制, 2012, 40(22)： 38-44.

XU Guo-jun1, LIU Yong-sheng, LI Ti-yin, et al. Study on the impact of electric vehicles charging load integrated into distribution network based on analytic hierarchy process and probabilistic simulation[J]. Power System Protection and Control, 2012, 40(22)：38-44.

[7] 张学清, 梁军, 张利, 等. 计及风光电源的一种地区电网电动汽车充电调度方法[J]. 电工技术学报, 2013, 28(2)： 28-35.

Zhang Xueqing Liang Jun Zhang Li, et al. Approach for Plug-in Electric Vehicles Charging Scheduling Considering Wind and Photovoltaic Power in Chinese Regional Power Grids[J]. Transactions Of China Electrotechnical Society, 2013, 28(2)： 28-35.

[8] 葛少云, 黄镠, 刘洪. 电动汽车有序充电的峰谷电价时段优化[J]. 电力系统保护与控制, 2012, 40(10)：2-5.

Ge Shaoyun, Huang Liu, Liu Hong. Optimization of peak-valley TOU power price time-period in ordered charging mode of electric vehicle[J]. Power System Protection and Control, 2012, 40(10)： 2-5.

[9] 张昌华, 孟劲松, 曹永兴, 等. 换电模式下电动汽车换电充裕度模型及仿真研究[J]. 电网技术, 2012, 36(9)： 15-19.

Zhang Changhua, Meng Jingsong, Cao Yongxing, et al. A Battery Swapping Requirement Adequacy Model for Electric Vehicles and Its Simulation Research[J]. Power System Technology, 2013, 36 (9)：15-19.

[10] Owen Worley, Diego Klabjan. Optimization of Battery Charging and Purchasing at Electric Vehicle Battery Swap Stations[C]. Vehicle Power and Propulsion Conference (VPPC). Chicago： IEEE, 2011： 1-4.

[11] Thoralf Winkler, Przemyslaw Komarnicki, Gerhard Mueller. Electric vehicle charging stations in magdeburg[C]. Vehicle Power and Propulsion Conference (VPPC). Dearborn： IEEE, 2009： 60-65.

[12] 占恺峤, 宋永华, 胡泽春, 等. 以降损为目标的电动汽车有序充电优化[J]. 中国电机工程学报, 2012, 32(31)： 11-18.

Zhan Kaiqiao, Song Yonghua, Hu Zechun, et al. Coordination of electric vehicle charging to minimize active power losses[J]. Proceedings of the CSEE, 2012, 32 (31)： 11-18.

[13] A. N. Brooks. Vehicle-to-Grid Demonstration Project：Grid Regulation Ancillary Service with a Battery Electric Vehicle. AC Propulsion, Inc., San Dimas, CA. Tech. Rep. 01-313, Dec. 10, 2002.

[14] J. R. Pillai, B. Bak-jensen. Integration of Vehicleto-Grid in the Western Danish power system[J]. IEEE Trans. Sustainable Energy, 2011(2)： 12-19.

[15] 王锡凡, 邵成成, 王秀丽, 等. 电动汽车充电负荷与调度控制策略综述[J]. 中国电机工程学报, 2013, 33(1)： 1-10.

Wang Xifan, Shao Chengcheng, Wang Xiuli, et al. Survey of Electric Vehicle Charging Load and Dispatch Control Strategies[J]. Proceedings of the CSEE, 2013, 33 (1)： 1-10.

[16] KEMPTON W, LETENDER S. Electric vehicles as a new power source for electric utilities[J]. Transportation Research： Part D, 1997, 2(3)： 157-175.

[17] 秦祯芳, 岳顺民, 余贻鑫, 等. 零售端电力市场中的电量电价弹性矩阵[J]. 电力系统自动化, 2004, 28(5)： 16-24.

Qin Zhenfang, Yue Shunmin, Yu Yixin, et al. Price Elasticity Matrix of Demand in Current Retail Power Market[J]. Automation of Electric Power System, 2004, 28 (5)： 16-24.

[18] 吴月萍, 杜奕. 改进的人工鱼群算法的参数分析[J].计算机工程及其应用, 2011, 48(13)： 50-51.

Wu Yueping, Du Yi. Parameters analysis of improved artificial fish swarm algorithm. Computer Engineering and Applications[J]. Computer Engineering and Applications, 2011, 48 (13)： 50-51.

[19] L. X. Chen, G. J. Liu. Optimization design of electromagnetic system based on adaptive improved behavior of artificial fish swarm algorithm[J]. Low Voltage Apparatus, 2012, 23： 17-21.

Research on Control Strategy for the Uniform Charging of Electric Vehicle Battery Swapping Station

Zhang Qidong Huang Xueliang Chen Zhong Chen Lixing Xu Yunpeng
（School of Electrical Engineering Southeast University Nanjing 210096 China）

In this paper, price model is established considering car owners’ interaction will based on the scale of charging and discharging load model of EVs, guide the orderly charging behavior through the battery change price, so as to realize the strategy of power grid peak shaving, genetic algorithm is used to solve the optimal real-time electricity price model. Finally, taking the battery changing stations economic operation and the charge and discharge machine state switching frequency optimal as the goals, using intelligent algorithm to solve the scheduling model, the optimal operation model of the EVs’ battery changing station cluster control is set up to meet the users’ demand for batteries.

Electric vehicle, smart grid, battery swapping station, coordinated charging, dispatching strategy

TM715; TM910.6

张齐东 女，1990年生，硕士研究生，研究方向为电动汽车与电网互动、智能电网。

国家高技术研究发展计划(863计划) 资助项目（No.2012AA050210）。

2014-09-22

黄学良 男，1969年生，教授，博士生导师，研究方向为无线电能传输技术、电力电子技术在电力系统中的应用、智能用电技术。