平均电流损耗时间法在配网线损计算中的应用

付学谦 陈皓勇

平均电流损耗时间法在配网线损计算中的应用

付学谦 陈皓勇

（华南理工大学电力学院 广州 510640）

配电网电能损失率是供电企业非常重要的技术经济综合性指标。本文采用平均电流损耗时间法对配电网的线损进行计算，并对最大负荷损耗时间法、损失因数法、方均根电流法和平均电流法的数学推导公式进行了物理概念的介绍。平均电流损耗时间法算法简单，易于实现，去除和弱化了假定条件，有利于提高线损计算精度。

负荷率 理论线损 损失因数 功率因数

1 引言

电量损耗最常用的计算方法有最大负荷损耗时间法、损失因数法、方均根电流法、平均电流法和等值功率法。文献[1]对最大负荷损耗时间法提出了质疑，指出功率因数cosφ含义不明确，未确定是平均功率因数还是最大负荷时的功率因数或另有其他含义。文献[2]指出最大负荷损耗时间法的计算精度主要取决于最大负荷损耗时间τ的误差大小，并通过分析证明在线路充电功率较大或在有无功补偿的情况下，最大负荷损耗时间法失效。用损失因数法推导等值最大负荷损耗时间τ可避免使用功率因数，其值由负荷率计算得到。文献[1-2]对理论线损计算的研究中忽略了一个重要误差，即最大负荷值的误差。等值功率法计算电能损耗时需要用到计算时段内的有效值，电量推导平均值计算的线损值偏小，需要考虑方差对线损计算的影响[3-4]。利用形状系数计算等效功率时，使用形状系数的平均值代替实际值会不可避免地导致相对误差。最小负荷率大于0.4时，相对误差在10%以内。文献[5]提出基于损失系数计算线损的方法，利用负荷曲线的平均值和偏离量的信息计算损失系数。该方法忽略了电流曲线和有功负荷曲线形状的区别，计算线损时没有区分有功负荷曲线和电流曲线。

本文分析了最大负荷值和电压值计算线损的缺点，基于平均电流损耗时间的概念提出了有功负荷曲线和电流曲线计算理论线损的方法，并与传统线损计算方法进行比较。在Matlab软件环境下搭建配电网仿真模型对实际运行电网数据进行仿真，采用平均电流损耗时间法对理论线损进行计算研究。

2 常用算法

2.1最大负荷损耗时间法

设ΔA为线路电能损耗，S为线路的视在功率，V为线路线电压，R为线路电阻，ΔPmax为最大负荷时线路的有功功率损失。则有

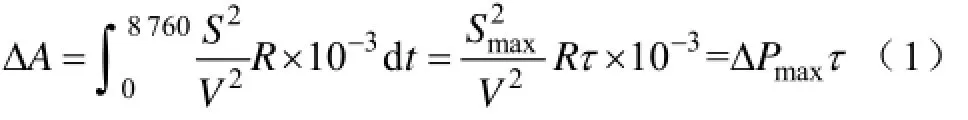
如果线路中输送的视在功率一直保持为最大负荷功率Smax，在τ小时内的能量损耗等于线路全年的实际电能损耗，则称τ为最大负荷损耗时间[6]。假定电压V恒定不变，可得

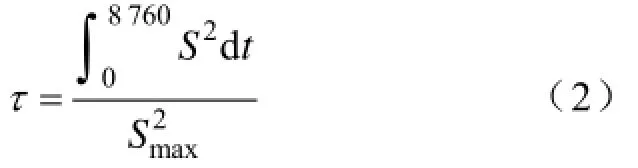
可见，最大负荷损耗时间与视在功率负荷曲线形状和最大视在功率有关。

2.2 平均电流法

平均电流法也称形状系数法，计算电能损耗公式为

式中，Iav为平均电流；k为负荷曲线形状系数，其值为方均根电流与平均电流之比。

2.3损失因数法

损失因数F等于计算时间T内的平均功率损耗ΔPav和最大负荷功率损耗ΔPmax之比，即式中，Ieff为方均根电流值；Imax为最大电流；f为负荷率。

电能损耗ΔA用损失因数F和最大负荷功率损耗ΔPmax表示，即

损失因数F与负荷率f和最小负荷率a的关系为[7]

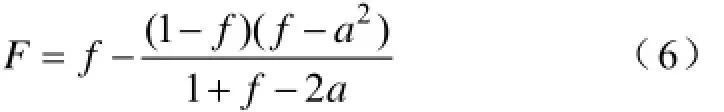
文献[8]中对几个国家损失因数F的经验公式进行了介绍，其中，英国和澳大利亚经验公式为美国城市和农村电网经验公式分别为

2.4方均根电流法

设计算时间内共有N个电流值，Ii为第i个电流值，方均根电流Ieff计算式为

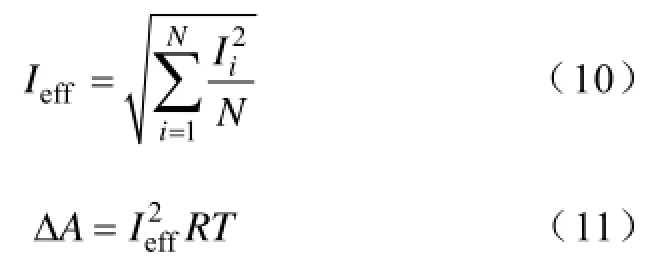
3 最大负荷值和电压值分析

3.1最大负荷值

3.1.1 离散型

负荷曲线是连续曲线，在供电企业实际运营中负荷数据一般按照一定时间间隔采集，是离散的数字量。广州电网负荷数据采集时间隔最小为15min。以广州市东城大酒店的有功负荷数据进行分析，某日的最大功率为56.616kW，功率因数为0.92。96点负荷数据由按照15min的间隔导出，48点和47点有功功率负荷曲线中每个点的数据依次是96点负荷数据中2个点数据值的平均值，即时间间隔为30min。48点负荷曲线的第一个点为96点负荷曲线前两个点的数据平均值，47点负荷曲线第一个点为96点负荷曲线第2点和第3点的平均值。以该日最大功率56.616kW作为基准值，对96点、48点和47点有功功率负荷曲线标幺化，如图1所示。

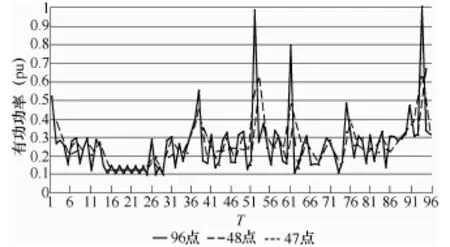
图1 96点、48点和47点负荷曲线Fig.1 96 point, 48point and 47point load curve

由图1可知，96点负荷曲线和48点、47点负荷曲线最大负荷值不相同。96点负荷曲线最大负荷值为1，而48点和47点负荷曲线最大负荷值分别为0.66和0.49。很明显对于同一负荷曲线，96点负荷曲线比和48点和47点负荷曲线更加准确。负荷数据采集时间区间大小对采集最大负荷数据值影响很大。当采集数据的时间间隔相同时，受最大负荷值采集起止时间影响。负荷曲线本身为预测数据，采集时间间隔内负荷变动越小，采集结果越准确。利用最大负荷值计算理论线损将存在误差，即采集时间间隔内的负荷变动对计算准确度的影响。

96点、48点和47点有功功率负荷曲线最大值和平均值由表1所示。

表1 96点、48点和47点负荷曲线Tab.1 96point, 48point and 47 point load

96点和48点有功功率负荷曲线计算的平均负荷值相同。采集起止时刻相同时，负荷数据采集时间间隔内的负荷突变对平均负荷数据值没有影响。48点和47点有功功率负荷曲线计算的平均负荷值相差很小，受起止两个时间点有功功率值的影响，当统计时间足够长采集点数足够多时，该差值可趋于0。

3.1.2 偶然性

图2所示为广州市东城大酒店的某月份的有功功率负荷曲线。

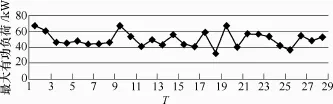
图2 最大负荷曲线Fig.2 Maximum demand curve

由图2可知，日最大负荷值是一个随机变量，具有偶然性的特点。随机变量的取值具有不确定性，因此将最大负荷值当作某个确定的数字来处理具有一定的风险。

3.2电压值

图3所示为广州市东城大酒店某日的三相电压数据，采集时间间隔为1h，每4个点采集一次。由图3可知实际运行电网的电压值是一个在一定范围波动的值，并不是恒定的。因此将电压值当作某个确定的数字来处理，必然给线损的计算带来误差。

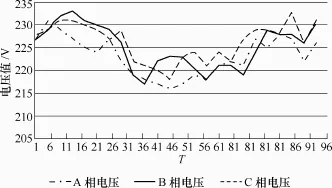
图3 日电压曲线图Fig.3 Daily voltage curve

4 平均电流损耗时间法

4.1基本原理

假定线路向一个集中负荷供电，如图4所示。

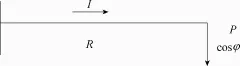
图4 简单供电网Fig.4 Simple circuit for anaysis

在计算时间T=NΔt内，设Ii为第i个电流值，Iav为电流的代数平均值，Ii,dif为Ii偏离Iav的差值，可得

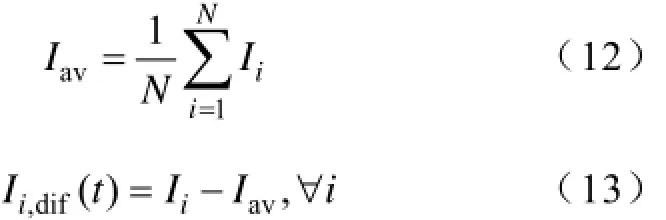
设R为恒阻抗，线损公式可以表示为

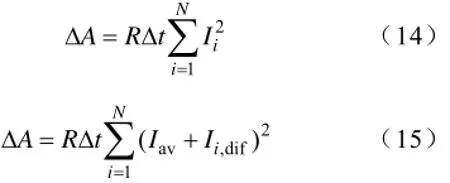
由于Ii,dif的代数和为0，可得

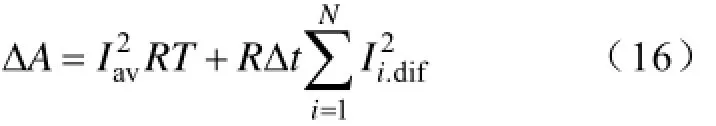
进一步化简可得

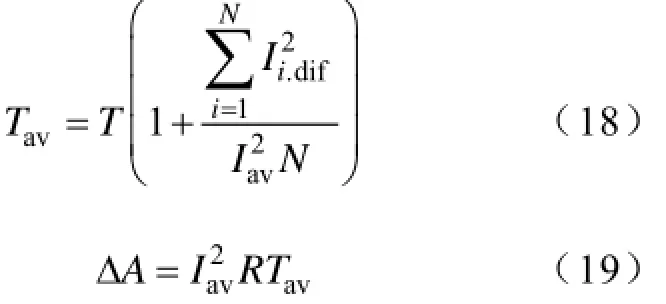
式中，Tav为产生等效损耗所需要的平均电流作用时间，称为平均电流损耗时间。平均电流损耗时间法不涉及损失系数的概念，引入平均电流损耗时间的概念。

平均电流损耗时间法用于计算变压器损耗时的计算式为

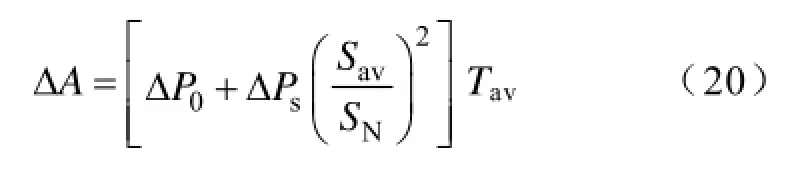
式中，ΔP0为空载损耗；ΔPs为短路损耗；SN为三相额定容量；Sav为视在功率平均值。

由于电压曲线和功率因数的影响，有功负荷曲线和电流曲线计算的平均电流损耗时间不同。在各时间点的电流值难于获得的情况下，如电网规划中，可以采用有功负荷值代替电流值计算理论线损。用平均有功负荷Pav代替平均电流Iav，设Pi为第i个有功负荷值，Pi,dif为Pi偏离Pav的差值，可得

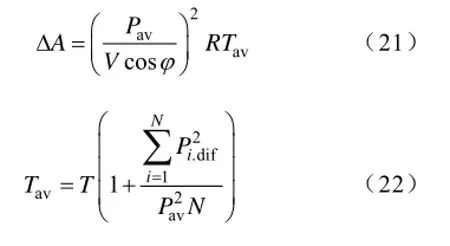
如果没有无功数据，用有功负荷计算出的线损值比用实际电流计算的结果误差大。

4.2本质分析

平均电流法的物理概念是在等效损耗时间阻抗中流过的平均电流所产生的电能损耗相当于实际负荷电流在计算时间内所产生的电能损耗。各时间点电流值的准确完整采集使得线损计算变得很简单。实际运行的电网对于电流值信息的采集不是实时的，有一定的时间间隔。每一时刻点采集的电流值具有离散性、偶然性和波动性的特点。平均电流损耗时间法通过电流的代数平均值求电能损耗，削弱了偶然的畸变值对最终计算值的影响，并将离散性、偶然性和波动性情况作为平均电流损耗时间的原始信息。对于同一负荷电流，不同采集时间间隔的负荷曲线的最大负荷损耗时间相同。平均电流损耗时间法本质为利用负荷电流曲线信息对理论线损进行的精确估算。

4.3与常用算法的区别联系

平均电流损耗时间法作为一种新的理论线损计算方法与常用算法既有区别又有联系。

4.3.1 最大负荷损耗时间法

（1）联系。最大负荷损耗时间τ可由平均电流损耗时间Tav推导，即

最大负荷损耗时间法计算线损，τ由最大负荷利用小时数Tmax和功率因数cosφ查表得到。可以由式（23）和查表法进行相互验证。

（2）区别。平均电流损耗时间法避免了功率因数cosφ、误差较大随机性较强的最大负荷值，同时避免了电网电压偏差对线损计算的影响。

4.3.2 平均电流法

本文所提算法的平均电流损耗时间法与平均电流法不是同一概念。平均电流法是由方均根电流法派生出来的一种理论线损计算方法，计算时间是实际负荷作用时间，需要利用方均根电流与平均电流关系计算形状系数。平均电流法计算的电能损耗偏小，需要乘以大于1的修正系数[10]，修正系数由负荷率和最小负荷率推导。平均电流损耗时间法计算理论线损不需要进行修正。

4.3.3 损耗因数法

（1）联系。损耗因数F可由平均电流损耗时间Tav推导，即

由式（24）可以验证计算损失因数F时选择的经验公式是否合理。

（2）区别。平均电流损耗时间法避免了使用经验公式，不受经验公式使用条件的限制。

4.3.4 方均根电流法

（1）联系。由方均根电流和平均电流损耗时间计算线损公式可知，两种方法均由原始公式（14）推导得出。

（2）区别。平均电流损耗时间法利用电流代数平均值计算理论线损，而非方均根电流。方均根电流法计算时间为实际负荷作用时间，平均电流损耗时间Tav值大于实际负荷作用时间。

5 算例分析

5.1算例1

以广州电网环风变电站10kV馈线F42为例，采用平均电流损耗时间法、损失因数法和等值功率法对该馈线某日的理论线损进行计算分析。其中电流采集时间间隔为15min，F42使用ZRYJV22-3×240电缆，如图5所示。

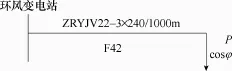
图5 环风变电站F42馈线Fig.5 A 10kV feeder

该10kV馈线A相电流2013年5月21日的日负荷电流曲线如图6所示。

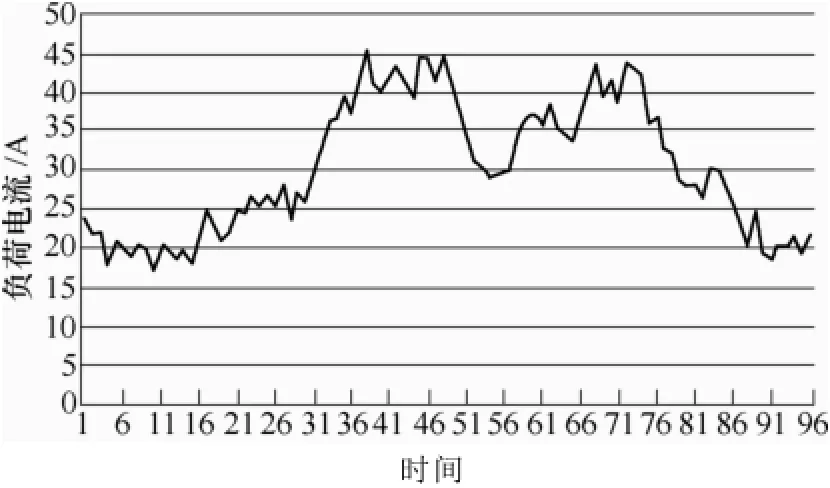
图6 日负荷电流曲线Fig.6 Daily electric current curve

由平均电流损耗时间Tav推导损失因数F，并与国外损失因数F的经验公式计算结果作比较，如表2所示。

表2 损失因数值Tab.2 Loss factor values

由表2可知，采用平均电流损耗时间法推导出的损耗因数F与经验公式计算值的结果接近，证明了利用平均电流损耗时间Tav验证损失因数F具有可行性。

损失因数法计算理论线损时，本文选用式（8）进行计算。平均电流损耗时间Tav计算值为25.817 74h，大于24h计算时间。采用损失因数法计算理论线损得到的最大负荷功率损耗时间FT值为11.801 242 75h，小于计算时间，其他关键参数值如表3所示。

表3 关键参数值Tab.3 Parameter Values

环风变电站F42线路的实际线损和理论线损计算值如表4所示。

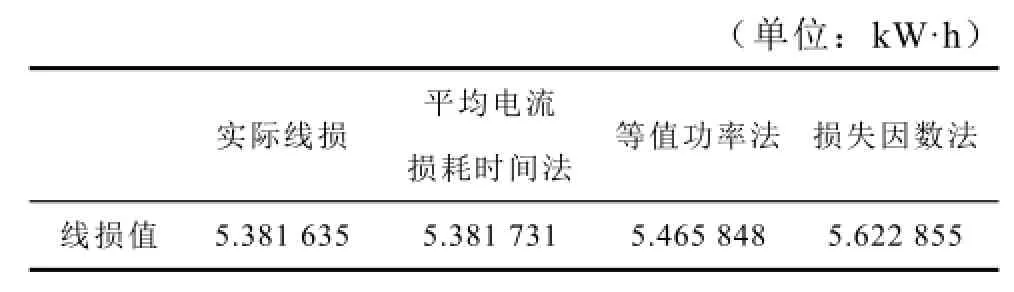
表4 算法的准确性比较Tab.4 Performance comparison

F42馈线网络拓扑结构简单，可认为管理线损为0，将实际线损视为理论线损真值。基于平均电流损耗法计算出的理论线损与真值最为接近。

5.2算例2

环风变电站F10配电线路仿真电路如图7所示，其中电流值采集时间间隔为1h，日采集电流点数24个。

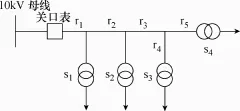
图7 配网拓扑结构Fig.7 Distribution network topology structure

图7 中，用户s1为一商务大厦，用户s2为食品药品监督局，用户s3为房屋管理所，用户s4为一工程建设单位。计算日的二次侧A相电流曲线如图8所示。

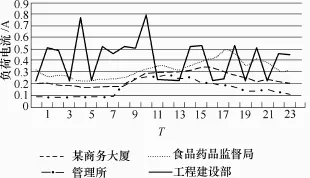
图8 日负荷电流曲线Fig.8 Daily electric current curve

平均电流损耗时间Tav计算值和采用损失因数法中的FT值如表5所示，单位为h。

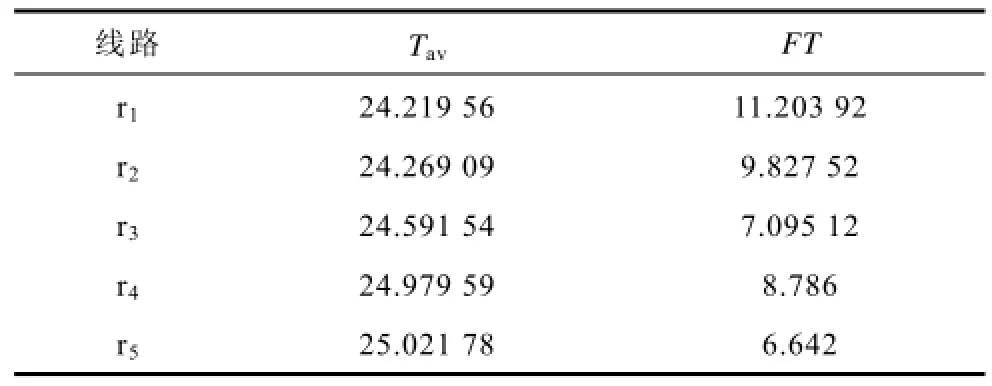
表5 时间参数值Tab.5 Time parameter values

F10线路的理论线损计算的结果如表6所示，单位为kW·h。由计算值可知，平均电流损耗时间与等值功率法、损失因数法、方均根电流法和平均电流法的计算结果相差不大。最大负荷损耗时间法通过查表法计算全年电能损耗，日电能损耗计算值与其他方法相比误差较大。

表6 理论线损计算结果Tab.6 Theoretical line loss value

电能损耗的计算一般用于规划和经济计算中，通常采用最大负荷损耗时间法。由仿真结果可知，最大负荷损耗时间法计算结果与平均电流损耗时间法的电能损耗计算值相差53.12kW·h。按照1kW·h电价0.89元计算，1年相差17 256元。对于该仿真配网，平均电流损耗时间法计算线损需要4个采集点的电流值。每个采集点的年运行维护成本小于4 314元时可挽回线损计算不准确导致的费用。

6 结论

本文对配电网的理论线损计算公式进行了详细的推导，提出了平均电流损耗时间法。该方法利用负荷电流曲线信息得到平均电流损耗时间Tav和各时间点电流值计算理论线损，计算逻辑简单，结果准确。平均电流损耗时间法基于各个时间节点的电流值或功率值。由于多功能电能表和计量自动化系统终端的发展应用，电网可以在获得电量数据的同时获得电流数据和负荷数据。由于不需要购置额外设备获得电流值或功率值，平均电流损耗时间法具有工程可行性和优越性。

[1] 陆广香, 单渊达, 龚乐年, 等. 最大负荷损耗小时数求取方法质疑[J]. 电工技术学报, 1996, 2(11)：54-59.

Lu Guangxiang, Shan Yuanda, Gong Lenian, et al. The method aboutthe determination of maximum load’s loss hours is doubtful[J]. Transactions of China Electrotechnical Society, 1996, 2(11)： 54-59.

[2] 霍佳丽, 王主丁, 聂崇峡. 电能损耗近似计算常用方法的误差分析[J]. 电网技术, 2009, 33(8)： 50-56.

Huo Jiali, Wang Zhuding, Nie Chongxia. Error analysis of widely used electric energy loss calculation methods [J]. Power System Technology, 2009, 33(8)： 50-56.

[3] Goswami S K, Basu S K. A new algorithm for the reconfiguration of distribution feeders for loss reduction [J]. IEEE Trans. on Power Systems, 1992, 7(3)： 1484-1491.

[4] 杨秀台. 电力网线损的理论计算与分析[M]. 北京：水利电力出版社, 1985.

[5] Leonardo M O Queiroz, Marcio A Roselli, Celso Cavellucci, et al. Energy losses estimation in power distribution systems[J]. IEEE Transactions on Power System, 2012, 27(4)： 1879-1887.

[6] 何仰赞, 温增银. 电力系统分析[M]. 武汉： 华中科技大学出版社, 2001.

[7] 霍佳丽, 王主丁, 聂崇峡. 电能损耗近似计算常用方法的误差分析[J]. 电网技术, 2009, 33(18)： 50-56.

Huo Jiali, Wang Zhuding, Nie Chongxia. Error analysis of widely used electric energy loss calculation[J]. Power System Technology, 2009, 33(18)： 50-56.

[8] Pabla A S. Electric power distribution[M]. New York：McGraw-Hill, 2004.

[9] 广东电网公司. 线损理论计算与应用[M]. 北京： 中国电力出版社, 2009.

[10] 李文琦. 含分布式发电的配电网网损分析[D]. 北京：华北电力大学, 2012.

Energy Losses Estimation Using Equivalent Time of Average Current Loss Method

Fu Xueqian Chen Haoyong
（School of Electric Power South China University of Technology Guangzhou 510640 China）

Power distribution network loss rate is a very important comprehensive technical and economic indicator in power enterprises. An alternative approach is proposed to evaluate energy losses estimation in electric power distribution networks, relying on the average current instead of the maximum demand. The physical conceptual analysis on the mathematical derivation of the equivalent hours of maximum loss, loss factor, rms current and average-current methods is introduced. The equivalent time of average current loss method can be regarded as an effective method to enhance the quality of information in loss estimation analysis. It eliminates and weakens the assumed conditions. Furthermore, it is helpful to improve the precision of energy losses estimation.

Load factor, theoretical line loss, loss factor, power factor

TM751

付学谦 男，1985年生，博士研究生，主要研究方向为电能质量监测控制评估，分布式发电优化规划与运行。

国家自然科学基金资助项目（51177049）；国家优秀青年科学基金资助项目（51322702）。

2013-09-13 改稿日期 2013-11-18

陈皓勇 男，1975年生，教授，博士生导师，本文通信作者，主要研究方向为电力市场，电力系统优化规划与运行。