无极灯用多阶高频谐振变换器负载匹配的研究
沈 豫 林国庆
无极灯用多阶高频谐振变换器负载匹配的研究
沈 豫 林国庆
(福州大学电气工程与自动化学院 福州 350116)
立足于无极灯用多阶高频谐振变换器,阐述了变换器的工作原理和稳态特性,引出了对高管压小功率无极灯进行负载匹配的关键问题。从起动时无极灯负载电阻很大,并且需要高压触发到稳态时灯电阻急剧变小,能够以最大功率输出以及实现开关管零电压开通等几个方面进行了理论分析和数学推导,充分考虑了无极灯负载自身在不同工作阶段的特点,得到了适合无极灯负载特性的匹配方案及其关键参数的设计方法。依据所提出的关键参数设计方法,研制了一台适用于不同工况的实验样机,实验结果证明了设计方法的有效性和可行性。
无极灯 多阶 谐振变换器 负载匹配 最大功率
1 引言
负载谐振变换器有利于改善电源性能,减小电感、变压器等磁性元件的体积和质量,提高变换器的功率密度,实现开关管的零电压开通(Zero Voltage Switching,ZVS)或者零电流关断(Zero Current Switching,ZCS)[1-3]。多阶负载谐振变换器由于兼具串联谐振和并联谐振的优点,应用越来越广泛。无极灯电子镇流器则是多阶负载谐振变换器在照明领域的典型应用[4-5]。无极灯没有电极,依靠电磁感应形成等离子气体放电的基本原理而发光,其放电的“伏安”特性呈负阻特性,必须与电子镇流器配合才能使用。电子镇流器与灯负载的良好匹配能够延长无极灯的使用寿命,提高无极灯工作的稳定性,对绿色照明的实施具有重要意义。
负载匹配是谐振变换器得到额定输出的关键。传统的电磁耦合依靠变压器变换阻抗进行负载匹配,高频下,这种方法对变压器的要求较高,成本也较高[6-7]。因此,采用多个无源器件通过不同拓扑结构改变阻抗的静电耦合匹配方法在国内外得到了广泛的重视[8-9]。文献[10-11]分别采用并联谐振变换器和CCL串并联谐振变换器,在负载匹配的过程中考虑了最佳工作点,并给出了参数设计的详细步骤,然而这两种电路结构由于缺少限流电感并不适用于具有负阻特性的无极灯负载。文献[12-13]基于品质因数远大于1这一假设对LLC谐振变换器进行了特性分析与负载匹配,方法简单易操作,但无极灯电子镇流器在起动和稳态时的负载等效电阻变化很大,品质因数相差较大,因此基于品质因数远大于1这一假设不成立;同时,这种电路无法为高管压的小功率无极灯负载提供点灯时所需的高压。
针对上述缺陷,本文结合无极灯负载在不同工作状态时的变化情况,对无极灯负载匹配的关键问题进行了研究,包括:起动时谐振变换器为近似于开路的无极灯负载提供点灯所需的高压;稳态时灯负载等效电阻急剧变小,无极灯能以最大功率输出并满足软开关条件。在此基础上,提出一种适合无极灯负载特性的匹配方案及其关键参数的设计方法。理论分析和实验结果表明,该方案是可行的。
2 无极灯用谐振变换器电路拓扑及工作原理
无极灯用高频谐振变换器的电路结构如图1a、1b所示,分别由电压型半桥逆变电路、串并联谐振网络和耦合线圈等组成。电压型半桥逆变电路由开关管Q1和Q2组成,VD1、VD2分别为开关管Q1、Q2体内二极管,C1、C2分别为开关管Q1、Q2寄生电容与外加并联电容之和。串并联谐振网络由电感Lr和电容Cr、Cb及耦合线圈等组成,耦合线圈由激励线圈和灯管等离子体放电体环组成。灯管等离子体放电环和若干匝的激励线圈之间可等效成一个耦合系数为k的变压器,其中激励线圈相当于变压器的一次绕组,等离子体放电环相当于变压器二次单匝绕组。半桥逆变电路将功率因数校正(PFC)电路输出的直流电压Udc变换成方波信号,再经谐振网络转换成高频交流信号,供给无极灯负载。
利用灯管等离子体放电环和激励线圈之间的耦合关系,将等效变压器二次侧等离子体放电环映射到变压器的一次侧,可以等效变换为等效电感Leq和等效电阻Req并联的形式[14]。起动时无极灯负载等效电阻Req很大,近似于开路;稳态时,无极灯负载等效电阻Req急剧变小。

图1 高频谐振变换器的电路结构及主要工作波形Fig.1 Circuit structure and main operational waveforms of high-frequency resonant converter
电路的主要工作波形如图1c所示。图中uin为半桥电路中点电压,iin为谐振回路输入电流,uo为谐振回路输出电压,ugs1和ugs2分别为逆变桥上、下开关管的驱动电压,tf为半桥中点电压uin从Udc下降到0的时间,td为死区时间,T为工作周期。
3 负载谐振变换器的阻抗匹配
无极灯的负载特性要求与之匹配的谐振变换器具有以下特性:①灯起动时负载电阻很大,谐振变换器能输出点灯所需高压;②稳态时灯电阻急剧变小,固有谐振频率发生变化,变换器应工作在最大功率输出;③参数变化时,开关管能实现软开关。
由于变换器工作在谐振回路固有谐振频率附近,电路中的有效成分都是正弦量,因此采用基波分析法对电路特性进行分析[15]。为分析方便,对电路进行如下假设:①变换器中所有的元件都是理想元件,变压器耦合系数k=1,等效电感Leq=Lc(Lc为激励线圈电感),等效电阻Req=Nc2Rl(Rl为灯电阻);②开关管Q1和Q2交替导通,uin是一个占空比为0.5、幅值等于Udc的方波;③变换器的工作频率f接近谐振回路固有谐振频率。
谐振变换器的拓扑结构以及谐振网络参数不同,谐振网络阻抗特性也不同。下面就图1所示两种电路结构分析它们与无极灯负载的匹配情况。
3.1电路结构1
根据图1a可以得到变换器的电压增益和谐振回路的输入功率为

其中,Z1(f)=1/(j2πfCb)+j2πfLr+[1/(j2πfCr)//j2πfLeq//Req]。谐振回路的电压增益和输入功率在两个频率点有极大值,如图2所示。

图2 谐振回路电压增益Mu和输入功率P与f的关系曲线Fig.2 Muvs. f & P vs. f
根据无极灯负载特性,取其中较高的频率作为工作频率,则有

该频率下,电压增益和谐振回路的输入功率为

由式(2)和式(3),可以得到f1=250kHz时,稳态输入功率Pm以及起动时电压增益Mum随电感Lr和电容比值Cr/Cb变化的三维曲线,如图3所示。从图中可以看出:Lr的取值越大,与之对应的Pm和Mum越小,即采用此电路结构与小功率负载匹配时无法获得点灯所需高压。因此,电路结构1不适用于高管压小功率灯负载。

图3 Pm与Cr/Cb、Lr以及Mum与Cr/Cb、Lr的关系曲线Fig.3 Pmvs. Cr/Cb、Lr& Mumvs. Cr/Cb、Lr
3.2电路结构2

根据图1b可以得到变换器的电压增益和谐振回路的输入功率为其中,Z0(f)=j2πfLr+1/(j2πfCr)//[1/(j2πfCb)+j2πfLeq// Req],同理可得

该频率下,电压增益和谐振回路的输入功率为

由式(5)和式(6),可以得到f0=250kHz时,稳态输入功率Pm以及起动时电压增益Mum随电感Lr和电容比值Cr/Cb变化的三维曲线,如图4所示。从图中可以看出:①当Cr/Cb较小时,对于小功率负载Lr的取值要大,但与之对应的Mum较小,无法获得点灯所需的高压。因此,Cr/Cb较小的取值不适用于小功率灯负载;②随着Cr/Cb增大,获取同样功率所需Lr减小,Mum增大。当Cr/Cb增大到一定值时,可以获得点灯所需高压。同时,Cr、Cb必须是nF级的电容,才能满足f0=250kHz这一条件。给定工作频率、额定功率以及灯起动所需高压的下限,由式(6)可以得到电感Lr的最大值Lr1。因此,只有Lr≤Lr1,谐振回路才能满足无极灯负载对灯起动高压的要求。

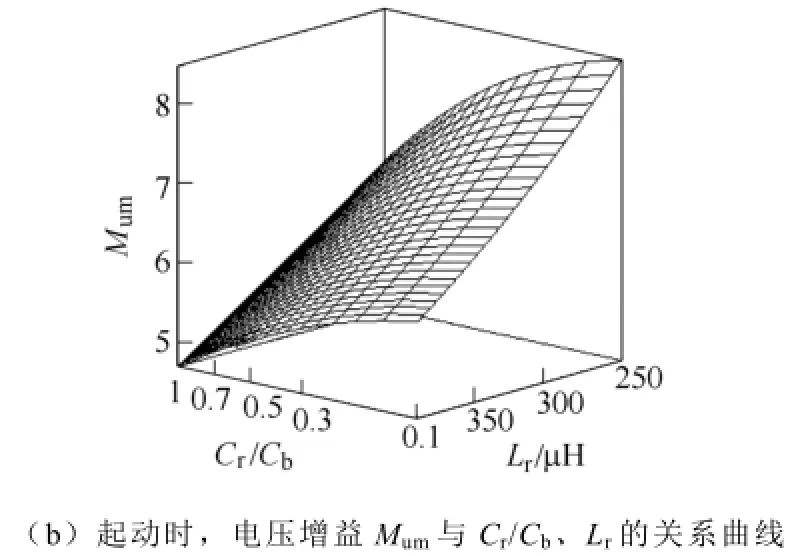
图4 Pm与Cr/Cb、Lr以及Mum与Cr/Cb、Lr的关系曲线Fig.4 Pmvs. Cr/Cb、Lr& Mumvs. Cr/Cb、Lr
从对两种电路结构的分析可以得出:当Cr/Cb较小时,在谐振回路中Cb的容抗可以忽略不计。此时,上述两种电路结构的谐振回路特性基本一致,且都不适用于小功率负载。当Cr与Cb可比拟时,电路结构1不适用于小功率负载,电路结构2适用于小功率负载。因此,采用电路结构2对小功率无极灯负载进行匹配。两种电路结构在Cr/Cb取不同值时谐振回路的特性对比如表所示。
4 电路结构2关键参数设计
4.1开关管的ZVS条件
图1c中,开关管Q1关断时,电容C2两端的电压uin从Udc下降到0的时间段tf内有

其中

式中,Iin为谐振回路输入电流iin的有效值;θ1为uin与uo间的相位差;θ2为uin与iin间的相位差。经化简可以得到

为了实现开关管的ZVS,必须为开关管的驱动设定合理的死区时间td,使tf≤td。

表 谐振回路特性表达式Tab. Expressions of resonance properties
4.2谐振参数计算
无极灯点火时,激励线圈承受最大的电压;稳定工作时,激励线圈传递无极灯的功率。因而在点火阶段,激励线圈磁心中的磁感应强度最大,为避免激励线圈磁心饱和、防止磁心过热,应限定激励线圈磁心中的磁感应强度。然后根据无极灯管径、功率Po、工作电压Uo、工作频率f0和磁感应强度等确定激励线圈匝数Nc和电感量Lc。最后再由式(5)、式(6)匹配出兼顾最大功率和点灯高压时的Lr、Cr和Cb。
(1)Lr的选取。令f0=250kHz,C1=C2=155pF,Po=55W,Uo=300V,Udc=400V,Lc=156μH,td= 280ns,由式(8)可以得到开关管两端电压下降时间tf随着Lr变化的曲线,如图5所示。可以看出: tf随Lr增大而增大,tf越小,则开关管越容易实现ZVS。给定死区时间td,由图5可以得到使开关管实现ZVS的电感Lr最大值Lr2。
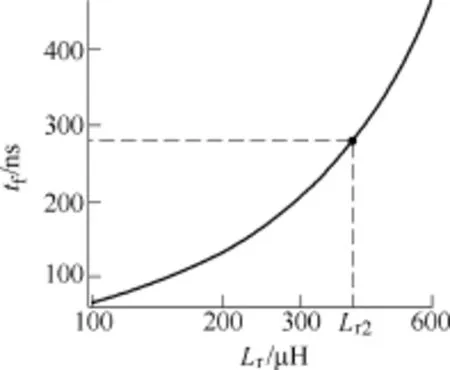
图5 开关管两端电压下降时间tf随Lr变化的曲线Fig.5 tfvs. Lr
结合图4b和图5可知,在参数设计时,Lr的取值越小,越能够兼顾起动时无极灯负载所需的高压和开关管实现ZVS的条件。因此,必须取Lr≤min(Lr1,Lr2);然而tf越小,开关管的关断损耗越大,因此选择Lr时应折中考虑。
(2)谐振电容的计算。Lr确定之后,依据无极灯负载对谐振回路的要求,变换器正常工作时需获得最大功率输出同时达到额定电压。因此,根据式(6)中的电压增益及最大功率表达式,可以推导出最大功率时,Cr和Cb的表达式为

5 实验结果
基于上述分析,设计了一台额定功率为55W、灯电压Uo=300V的电子镇流器原理样机。主要参数如下:PFC输出直流电压Udc=400V,谐振变换器频率f0=250kHz,激励线圈电感Lc=156μH,开关管两端并联电容C1=C2=155pF,死区时间td=280ns。实验结果如图6所示。
图6a、图6b所示分别为Lr=270μH和Lr=170μH时点火期间电压uo的波形。开机时,芯片电源上电到起动电压后芯片起振。芯片起动后,开始下扫频率,点灯电压uo逐渐上升最终将灯点亮。随后灯电阻迅速减小,uo额定输出。Lr=270μH点火时uo峰值为800V,低于Lr=170μH点火时uo峰值1 300V。即限流电感Lr越大,uo的峰值越小,与图4b相符。
图6c、图6d所示分别为Lr=270μH和Lr=170μH无灯开机时电压uo的波形。从图中可以看出,Lr=270μH无灯开机时uo峰值为1 500V,低于Lr=170 μH无灯开机时uo峰值2 200V。同样与图4b相符。
图6d、图6e所示分别为Lr=270μH和Lr=170μH稳态时半桥中点电压uin以及下管驱动电压ugs2的波形。从图6d、图6e可以看出,开关管都实现了ZVS,且Lr=270μH时稳态uin的电压下降时间为156ns,大于Lr=170μH时稳态uin的电压下降时间124ns,即限流电感Lr越小,电压下降时间越短,开关管越容易实现ZVS。与图5所示相符。


图6 实验波形Fig.6 Experimental waveforms
6 结论
本文结合无极灯负载特性,分析比较了两种电路结构与无极灯负载的匹配情况。电路结构1在与小功率无极灯负载匹配时需要较大的Lr值,而随着Lr值的增大将无法产生点灯所需的高压,因此不能与高管压小功率无极灯负载匹配;电路结构2在与小功率无极灯负载匹配时仅需要较小的Lr值,并能满足点灯高压条件,因此可与高管压小功率无极灯负载匹配。
针对高管压小功率无极灯负载提出一种能够兼顾最大输出功率、点灯高压和开关管ZVS条件的匹配方案及其关键参数设计方法。在此基础上,研制了一台55W适用于不同工况的无极灯电子镇流器原理样机。实验结果表明电路结构2可与高管压小功率无极灯负载匹配,且电感Lr越小,越容易获得点灯高压同时电路越容易实现软开关,验证了理论分析和设计方法的准确性以及可行性。
[1] 王镇道, 赵亚魁, 章兢, 等. LLC半桥式谐振变换器参数模型与设计[J]. 电工技术学报, 2012, 27(12):51-55.
Wang Zhendao, Zhao Yakui, Zhang Jing, et al. Parameter model and design for LLC resonant halfbridge converter[J]. Transactions of China Electrotechnical Society, 2012, 27(12): 51-55.
[2] Wang H, Zanchetta P, Clare J, et al. Modelling and control of a zero current switching high-voltage resonant converter power supply for radio frequency sources[J]. IEEE Transactions on Power Electronics, 2012, 5(4):401-409.
[3] 陈申, 吕征宇, 姚玮. LLC谐振型软开关直流变压器的研究与实现[J]. 电工技术学报, 2012, 27(10):163-169.
Chen Shen, Lü Zhengyu, Yao Wei. Research and verification on LLC resonant soft switching DC-DC transformer[J]. Transactions of China Electrotechnical Society, 2012, 27(10): 163-169.
[4] 沈豫, 林国庆, 唐建山. 无极灯电子镇流器频率跟踪控制技术研究[J]. 电工电能新技术, 2013, 32(1):52-55.
Shen Yu, Lin Guoqing, Tang Jianshan. Research on frequency tracking technology of electronic ballasts [J]. Advanced Technology of Electrical Engineering and Energy, 2013, 32(1): 52-55.
[5] Jang T, Kim H J, Kim H. Dimming control characteristics of electrodeless fluorescent lamps[J]. IEEE Transactions on Industrial Electronics, 2009, 56(1): 93-100.
[6] 潘天明. 现代感应加热装置[M]. 北京: 冶金工业出版社, 1996.
[7] Chudjuarjeen S, Sangswang A, Koompai C. An improved LLC resonant inverter for induction heating with asymmetrical control[C]. IEEE Industrial Electronics Conference, 2009: 1612-1617.
[8] Branas C, Azcondo F J, Casanueva R. A generalized study of multi-phase parallel resonant inverters for high-power applications[J]. IEEE Trans. on Circuits and Systems, 2008, 55(7): 2128-2138.
[9] 王春芳, 徐勤超. 变频微波炉电源用LLC谐振变换器[J]. 电工技术学报, 2012, 27(6): 103-109.
Wang Chunfang, Xu Qinchao. Study of LLC resonant converter for variable-frequence microwave oven power supply[J]. Transactions of China Electrotechnical Society, 2012, 27(6): 103-109.
[10] Fuentes R, Juliet J, Estrada J, et al. Design aspects and experimental results of a high power factor induction heating system[C]. IEEE Industrial Electronics Conference, 2009: 373-377.
[11] Zhang Z J, Li H M, Peng Y L. Induction heating power CCL static electricity coupling load matching analysis[C]. IEEE Region 10 Conference, 2008: 1-4.
[12] Chudjuarjeen S, Sangswang A, Koompai C. An improved LLC resonant inverter for induction heating with asymmetrical control[C]. IEEE Industrial Electronics Conference, 2009: 1612-1617.
[13] Chudjuarjeen S, Sangswang A, Koompai C. An improved LLC resonant inverter for induction heating applications with asymmetrical control[J]. IEEE Trans. on Industrial Electronics, 2011, 58(7): 2915-2925.
[14] Shen Y, Lin G Q. Research on control strategy of electronic ballast for electrodeless lamp[C]. IEEE Applied Mechanics and Materials Conference, 2013:2442-2445.
[15] 张卫平. 开关变换器的建模与控制[M]. 北京: 中国电力出版社, 2006.
Study of Load Matching of Multi-Order High Frequency Resonant Converter for Electrodeless Lamp
Shen Yu Lin Guoqing
(College of Electrical Engineering and Automation Fuzhou University Fuzhou 350116 China)
Focused on multi-order high frequency resonant converter for electrodeless lamp, this paper expounds operating principle and steady-state characteristics, leading to key issues of load matching. When starting up, electrodeless lamp needs high trigger voltage for its large equivalent resistance. Lamp resistance suddenly decreases as soon as it lit up. The converter outputs maximum power and zero voltage switching is realized in steady state. From these aspects, theoretical analysis and mathematical deduction are carried on. Matching scheme suitable for electrodeless lamp load characteristics and the design of key parameters are obtained taking into full account the features of electrodelss lamp at different operating stages. Based on the proposed design method, a laboratory prototype adapts to different working conditions has been built. Experimental results were proposed to confirm validity and effectiveness of the scheme presented.
Electrodeless lamp, multi-order, resonant converter, load matching, maximum power
TM46
沈 豫 女,1985年生,博士研究生,研究方向为电能的高频变换与控制技术。
2013-07-15 改稿日期 2013-10-29
林国庆 男,1966年生,教授,博士生导师,研究方向为电力电子变流技术。

