补 形
——求解三棱锥外接球半径的一条重要途径
2015-04-14 09:27崔磊
新课程(中学) 2015年11期
崔 磊
(江苏省平潮高级中学)
在立体几何的学习中,经常遇到求解三棱锥外接球体半径的问题,此类问题往往球心的位置难以找到。我们知道,棱锥是柱体的一部分,因此,在求三棱锥外接球体的半径时,通过“补形”,将锥体还原成柱体,有时能起到柳暗花明的效果。常见的“补形”方法有下列几种.
例1. 已知三棱锥P-ABC 中,PA⊥PB,PB⊥PC,PC⊥PA,且PA=3,PB=4,PC=5.则其外接球体的表面积为________.
思路:补成“长方体”
解析:三棱锥P-ABC(图1)可以补成长方体,且它们拥有相同的外接球体(图2),再过长方体的一组对面上的对角线作轴截面得一圆的内接矩形(图3).其中矩形的一边为原长方体的棱,另一边为原长方体的面对角线,而该矩形的对角线则为球体的直

图1

图2

图3
例2.已知一正四面体的棱长为4,则其外接球体的体积为________.
思路:补成“正方体”
解析:由于连接正方体的六条面对角线可以形成一个正四面体,因此,可将正四面体补成一个正方体,且它们拥有相同的外接球体(图4).再过该正方体的一组对面上的对角线作轴截面,易得外接球体的半径为,从而其体积为
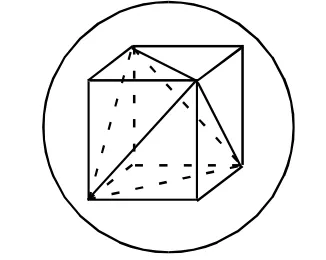
图4
例3.已知三棱锥P-ABC 中,底面ABC 为正三角形,边长为2,侧棱PA⊥底面ABC,且PA=2,则其外接球体的半径为 .
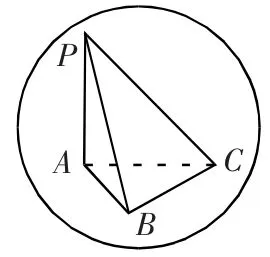
图5

图6

图7
思路一:补成“直三棱柱”

思路二:补成“圆柱”


图8

图9
总之,“补形”是求解三棱锥外接球体半径的一条重要途径,且通常可补成上述几种模型。“补形”应遵循“拥有相同的外接球体”的原则,在此基础上,还要选择好恰当的位置作出截面,将抽象的空间问题转化为熟悉的平面问题,关系也就简单明朗多了。
猜你喜欢
数学大王·低年级(2021年4期)2021-04-27
消费电子(2020年5期)2020-12-28
振动与冲击(2019年7期)2019-04-22
兵工学报(2019年2期)2019-03-13
福建中学数学(2018年1期)2018-11-29
中学数学研究(2008年9期)2008-12-09
中学数学杂志(高中版)(2008年4期)2008-07-31
中学数学杂志(高中版)(2008年1期)2008-02-23
中学数学杂志(高中版)(2006年4期)2006-07-19

