为什么要“一分为二”——由一道应用型问题的错解说起

☉江苏省如皋市东陈初中 杭石琴

为什么要“一分为二”
——由一道应用型问题的错解说起

☉江苏省如皋市东陈初中 杭石琴

题目：某地出租车计费方法如图所示，x（km）表示行驶里程，y（元）表示车费，请根据图像解答下列问题：

（1）当x＞2时，求y与x之间的函数关系式；

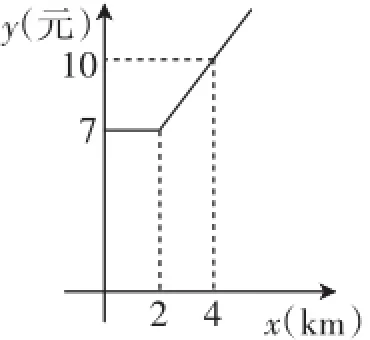
图1

（2）若某乘客有一次乘出租车的里程为18km，则这位乘客需付出租车车费多少元？

一、解法呈现

对比分析：对于（1），“用待定系数法求一次函数的解析式”，由于图像的直观呈现，绝大多数同学都能从图像中捕捉到两个点（2，7）、（4，10），用待定系数法求出了正确答案.但是解答（2）时，很多同学给出了上面的“出错解法”.这一解法，与“正确解法”相比，解题过程增加了一个“分段”的环节，学生将路程“一分为二分”（即2km和16km）分别计费，其中2km是应用“起步价”进行计费，收7元，而余下的16km所付费用则由（1）中的函数解析式求得.最终，通过简单相加，得到“需要付出租车车费35元”的结论.“用18减去2”，将解题者对题意的理解展露无余，学对题意理解的偏差，让他们在“错解之路”上迈出了一大步.

二、错因分析

学生的出错，起因多种多样.要想让他们在今后的问题解决中规避此类错误，就必须找出真正的错因.为此，在学生解答后，笔者对学生给出的解题过程进行了详细地分析，并与部分出错的同学进行了深入交流，最终，将这道题的出错进行了如下归因.

1.函数概念理解不清

函数是初中阶段的核心概念，而“单值对应”又是函数概念的核心，只有“变量x取一个值时，y有唯一确定的值与之对应”，变量y才是变量x的函数.与文本概念相对应的是，只有当两个变量在图像上也存在这种“一一对应”的关系时，纵轴所表示的量与横轴所表示的量之间才具有函数关系.就文中的题目而言，图像中所呈现出的车费y（元）与行驶里程x（km）之间的一一对应关系，正是函数关系的图像化体现.自然地，18km作为行驶的里程之一，也就应该对应着横轴上x的取值，在这个图像上自然就应该有与之对应的车费y（元）.在问题解答过程中，一些学生无视这种对应关系，将18km“一分为二”，将本题错误地理解为“分段付费”.这样的求解，充分说明他们对函数概念的认知是含糊的，尤其是对图像中的函数关系的辨析是不到位的.

2.生活经验干扰解题

很多以考查函数为背景的数学试题，都选择了与学生息息相关的生活情境作为问题背景，其中较为常见的有商品销售、分段计费（水、电等）、行程问题、工程问题等.本题中的“出租车付费”，同样来自于实际生活，是生活中较为常见的情境，每当人们谈到出租车付费，常会用“‘起步价’加上‘超出3km的部分每千米x元’”的方式付费.而事实上，由于出租车计价器的引入，乘坐出租车付费并不需要我们进行计算，只需直接按计价器付费（计价器已经按照既定我们常说的付费方式进行了设置）.所以我们常常陈述的这种付费方式仅仅停留在口头上.但在这道题的解答上，不少学生却将这种方法用了起来，误认为“前2km是按照起步价计费，后面的16km按照关系式计费”.显然，来自生活的经验，干扰了学生对函数本质的认知，看似对“这笔帐是如何算”了如指掌，实则忽视了数量之间的内在关系，另起炉灶用正确的说法求出了一个错误的答案，来自实际生活的经验对数学问题的解答开了一个不小的玩笑.

3.应用模型意识不强

数学来自于生活，而又服务于生活.所以在数学学习中，很多应用型问题的解答需要借助常见的数学模型，用一种较为固化的形式得出最终的答案.在初中阶段，应用型数学问题常与方程（组）、不等式（组）及函数等数学模型紧密关联，用好这些模型就能使问题顺利得解.以本题为例，图1中，车费y（元）实际上是行驶里程x（km）的一个分段函数，其解析式为第一问，“当x＞2时，求y与x之间的函数关系式”，是命题者为第二问进行的铺垫.学生给出了第一问的答案，却没能用好自己已经建构好的数学模型，错误地将18“一分为二”进行计费，绕了一个弯子给出的解题过程凸显了学生模型应用意识的薄弱，让命题者的良好初衷彻底落在了空处.

三、教学启示

1.关注生活问题与数学问题的互相转化

实际问题与学生的生活紧密关联，在学生熟悉的情境中，充实着复杂的数量关系.为了能让学生明晰这些数量关系，我们不仅要让他们经历生活问题向数学问题转化的过程，还要让他们经历数学问题向生活问题的转化，在这种有意识的互相转化中，让两种问题实现有效融通.这种不同性质问题的转化，既能培养学生的抽象思维，让他们将复杂的生活情境数学化，借助数学的工具解决；还能培养学生的形象思维，促进数学问题的生活化，以生活的角度分析问题.这种介于抽象与形象之间的互换，易于培养学生“设身处地”思考问题的思维习惯，有利于提高他们分析问题和解决问题的能力.如果有了长期的转化训练，学生完全可以将“题目”中的出租车的行驶里程用字母x替代，将出租车车费用字母y替代，这样一来，图像中的两条线就直接转化成y与x的关系了，第二问“乘出租车的里程为18km”就会被直接转化为“x=18”.在学生分析问题的过程中，生活问题的数学化和数学问题的生活化，自然会激活学生的生活经验和数学经验，那么“一分为二”求解的做法自然就不会出现了.所以当遇到实际问题时，我们要强化学生进行数学化分析，离情境远点，多谈谈数学的东西；当遇到数学问题时，我们也可以借助生活化的情境来帮助学生分析，用生活经验辅助学生的数学认知.

2.强化模型生成与模型应用的过程体验

数学模型“生来有用”，它生成于学生获取数学知识与应用数学知识的过程之中，是后续的学习和应用的重要工具.在化解数学问题时，建构有效的数学模型是解题的便捷通道.为了培养学生提取模型解题的习惯和应用数学模型的意识，我们不仅要重视新知教学中模型的建构，还要重视巩固训练中模型的应用.新知教学，我们应让学生经历完整的模型建构历程，充分体验到数学模型内在的“知识链”，感知到“四基”在模型中的固着点；巩固训练，我们可以安排模型适用性训练，通过编排适量的题组，将关键信息，如点、线、文本、表格等与数学模型联系起来，让学生在自主解答中形成自觉选择数学模型解决问题的意识.这种用以巩固的题组训练滞后于新知教学，但与学生解题技能的提升是同步的.题组训练可以是以某一种模型为主的专题训练，也可以是多个模型混合应用的综合性训练，只要达到强化模型的解题应用就行.模型的应用训练关键是要学生自主经历，要让他们全程经历题目的分析、模型的建构和模型的化解过程，从而积累宝贵的解题经验.在这种过程历练中，应突出模型与情境的关联，本文中的这道题就是将一个“分段函数”模型融合到了“出租车付费”问题之中，为了培养学生的模型应用意识，我们应让学生经历这道题目模型建构与化解的历程，逐步形成“提取有用信息”、建构适用模型的能力.

3.突出读题析文能力的培养

初中阶段的应用型问题，与前面学段相比，不仅题目的信息量大，而且信息的呈现方式也比较多.在众多的呈现方式中，主要有丰富的文本信息、复杂的图像信息和规范的表格信息.众多的问题信息通道，给学生的信息分析与获取设置了障碍.在教学中，为了让学生能够从题目中提取到“有用的解题信息”，我们应结合不同的信息呈现方式，对学生的审题进行指导.以本文中的这道图像信息题为例，这是一道以图像信息为主的应用型问题，遇到此类问题，我们应指导学生从图像入手，找出“线”的“起点”“拐点”“途中点”，深入剖析这些点的实际意义，通过组内和全班的交流，让题中的信息在图像与文本之间反复转化，从而生成有利于问题解决的函数模型.要想提升应用型问题的解答能力，培养学生的审题能力是起点.在我们的日常教学中，应立足于具体情境的“透视”分析，让学生对问题的情境不断揣摩与拆解，促进有效解题信息自然分离，从而让解题适用的数学模型自然“析出”.当学生经历长期的审题训练后，其读题析文的能力必然会增强，文图、文表、图表的呼应应该会变得较为顺畅，最终生成有利于问题解决的数学模型也就在情理之中了.Z