例谈初中数学开放题教学对学生思维品质的培养

☉江苏省昆山市石浦中学 潘田芬

例谈初中数学开放题教学对学生思维品质的培养

☉江苏省昆山市石浦中学 潘田芬

《义务教育数学课程标准》强调：“数学课程要面向全体学生，适应学生个性发展的需要，使得：人人都能获得良好的数学教育，不同的人在数学上得到不同的发展.”［1］教育部《中考改革指导意见》明确指出：“理科在试卷中适当增加开放性试题，培养学生的创新能力，初步体现素质教育的要求.”随着开放题在高考和中考数学试卷上的频频出现，对数学学科教学提出了一个新的课题，开放题教学研究就越来越受到广大数学教师的重视.下面结合初中数学新课程教学案例，就此作探讨.

一、初中数学开放题教学的内涵

戴再平老师的研究认为：“数学开放题是指那些答案不唯一，并在设问方式上要求学生进行多方面、多角度、多层次探索的数学问题.”［2］可见，数学开放题教学就是从学生的数学现实出发，把生产、生活中的现实数学问题，用数学语言将其数学化，即通过设计数学情境或建立数学模型来引导学生探索问题解决结果的教学过程和方法.

开放题教学具有探索性和拓展性，这是因为开放题教学具有非常规性、发散性和创新性，通常都要运用一定的数学思维方法来探索求解，而且在此过程中又会生成一些新的问题，从而发展成一系列的问题，或将问题加以推广，找出更一般、更有概括性的结论.

开放题教学需要学生的广泛参与，体现了学生的主体地位.这是因为开放题的答案是不确定的，解答过程具有层次性，能满足各层次水平学生的需求，使全体学生都能参与到对问题的探索解答过程中，在自己的能力范围内解决问题，得到不同深度的答案.开放题的条件有时会不足，要求学生予以补充，有时会多余，要求学生进行选择，才能着手解题.

因此，在教学过程中，富有技巧地设计一些开放性问题，恰到好处地搭建一个开放性的教学平台，不但有利于培养学生的数学思维品质，更有利于因材施教，实施个性化教学，对于实现学生“四基”（基础知识、基本技能、基本思想、基本活动经验）培养目标也具有重要意义.

二、初中数学开放题教学的初步实践

1.运用条件不唯一型开放题，培养学生思维的深刻性

案例1：（2013年盐城市中考题）写出一个过点（0，3），且函数值y随自变量x的增大而减小的一次函数关系式：_________.（填上一个答案即可）

思路分析：此题可用待定系数法来解决.设此一次函数关系式是y=kx+b（k≠0）.把x=0、y=3代入得：b=3.根据y随x的增大而减小，知k＜0.此条件包含的答案不唯一，故此题只要给定k为一个负数，如k取-1，则y=-x+3.

反思：条件不唯一型开放题，所给条件包含着答案不唯一的因素.在解题过程中，学生必须迁移已有知识，结合有关条件，从不同角度对问题作全面分析，正确判断，得出结论，这能培养学生思维的深刻性.本题的条件“函数值y随自变量x的增大而减小”，表明答案不唯一，此时要求学生根据一次函数的增减性做出正确的判断，并给定k为任一个负数即可得解.

2.运用结论未知型开放题，培养学生思维的求异性

案例2：（2005年济宁市中考题）结合生活中的实例，（1-15%）x可以解释为_________.

思路分析：此题主要考查学生对代数式表示意义的理解和掌握，学生只要结合生产、生活实际，用数学模型解释清楚就行，其答案不唯一，如：一件商品的原单价为x元，降价15%后的单价是（1-15%）x元.

反思：这类问题因其结论具有多样性，所以学生能从多角度、多层次、多侧面来思考问题，这对于适应学生个性发展，使学生养成求异思维、发散思维的学习习惯，提高学生观察生活、发现问题、分析问题、迁移知识、解决问题的能力都很有益处.

3.运用条件隐藏型开放题，培养学生思维的缜密性

案例3：（2011年牡丹江市中考题）如图1，△ABC的高BD、CE相交于点O.请你添加一对相等的线段或一对相等的角的条件，使BD=CE.你所添加的条件是_______.

图1

思路分析：由△ABC的高BD、CE相交于点O，可得∠BEC=∠CDB=90°，或可得∠AEC=∠ADB=90°，要使BD=CE，只需证明△BCE≌△CBD或△ACE≌△ABD即可.根据全等三角形的判定定理与性质，要证△BCE≌△CBD，除了∠BEC=∠CDB=90°外，可根据图形挖掘出隐含条件BC=CB，还要添加一对相等的线段：BE=CD；或添加一对相等的角：∠EBC=∠DCB或∠DBC=∠ECB.若证△ACE≌△ABD，除了∠AEC=∠ADB=90°外，可根据图形挖掘出隐含条件∠A=∠A，还要添加AC=AB或AE= AD.故此题答案不唯一.

反思：条件隐藏型开放题，是指解题所需的某些条件隐藏在题目中，如不注意容易遗漏.在解题时既要充分利用已知的条件，又要挖掘与问题有关的隐藏的条件.这样有利于学生养成认真细致的审题习惯，培养学生思维的缜密性.

4.运用多向型开放题，培养学生思维的广阔性和灵活性

案例4：如图2，已知线段AB，C为线段AB上任一点，M、N分别为AC、BC的中点，若AB=10cm，BC=4cm，求MN的长.

图2

解：由AB=10cm，BC=4cm，得AC=AB-BC=10-4=6（cm）.

变式1：若AB=10cm，BC=6cm或BC=8cm，…，发现MN恒等于5cm；若AB=8cm，BC=4cm，发现MN=4cm；求证MN的长与BC的长度无关，始终等于AB的一半.

变式2：将题中“C为线段AB上任一点”改为“C为线段AB的延长线上任一点”（如图3），M、N分别为AC、BC的中点，此时MN与AB又有怎样的数量关系？

图3

变式3：角的计算与线段的计算存在着紧密的联系，它们之间可互相借鉴解法，请你模仿设计一道以角为背景的计算题.

解：（1）如图4，OC是∠AOB内任一条射线，OM、ON分别平分∠AOC和∠BOC.

①若∠AOC=30°，∠AOB=90°，求∠MON的度数；

②猜想∠MON与∠AOB有何数量关系，并说明理由；

（2）如图5，若OC是∠AOB外任一条射线，则∠MON与∠AOB的数量关系还成立吗？请说明理由.

图4

图5

反思：多向型开放题，可有多种思考方向，这样就可引导学生通过联想进行一题多变、一题多解、一题多思，以培养学生思维的广阔性和灵活性.此案例先让学生发现不管点C在线段AB上何处，两中点的距离MN始终等于AB的一半，由数的运算到线段数量关系的说理，逐步引导学生发现规律，并渗透数学整体思想，启发学生一题多解；接下来通过“变式”让学生发现不管点C在线段AB的上还是在线段AB的延长线上，MN始终等于AB的一半；最后运用类比转化，由线段问题联想到角的问题，引导学生发现角方面的相似规律.这样通过探究、交流、反思等活动，不仅引导学生发现了图形中蕴含的一般规律，还让学生体会了数形结合、转化、整体等数学思想，体验了由特殊到一般、分类讨论、类比等解题方法，培养了学生思维的广阔性和灵活性，提高了学生分析和解决问题的能力.

5.运用设计型开放题，培养学生思维的创新性

案例5：在一服装厂里有大量形状为等腰直角三角形的边角布料，现找出其中一种，测得∠C=90°，AC=BC= 4，今要从这种三角形中剪出一种扇形，做成不同形状的玩具，使扇形的边缘半径恰好都在△ABC的边上，且扇形的弧与△ABC的其他边相切，请设计出符合题意的方案示意图，并求出扇形的半径（只要画出图形，并直接写出扇形半径）.

思路分析：所设计的扇形要求满足两个条件.①弧线与三角形的边相切，有两种情形：与其中一边相切（直角边或斜边）；与其中两边相切（两直角边、一直角边和一斜边）.②半径都在三角形的边上，且尽量能利用边角料（即找到最大的扇形）.根据题意可设计出如下四种方案（.1）如图6，与一直角边相切，r1=4；（2）如图7，与一斜边相切，；（3）如图8，与两直角边相切，r3=2；（4）如图9，与一直角边和一斜边相切，r4=-4.

图6

图7

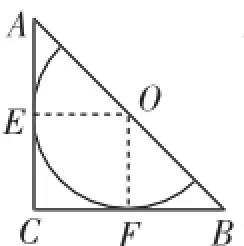
图8

图9

反思：设计型开放题是近年来出现的一种题型，代表一种命题的新思路.这类试题往往利用给定的几个基本图形，要求设计一个有意义的图形，一般背景新颖、形式活泼，主要运用添画、分割、剪拼等方法，主要考查学生的动手能力和实践能力，让学生在充满探索的过程中感受数学创造的乐趣，从而培养学生思维的创新性.

开放型试题已成为数学中考的热点试题之一.以上仅是笔者实践开放题教学的一瞥，要强调的是上述五例开放性问题对思维品质的培养是相互交叉、互相渗透、很难分清的，其区别仅在于侧重点不同而已.

1.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

2.戴再平，等.开放题——数学教学的新模式［M］.上海：上海教育出版社，2004.

3.张清芳.解决数学开放性问题对思维品质的要求［J］.云南教育，2006（2）.Z