瓦斯爆炸压力与波前瞬态流速演化特征及其定量关系

林柏泉，洪溢都，朱传杰，江丙友，刘 谦，孙豫敏

(1.中国矿业大学安全工程学院，江苏 徐州 221116； 2.煤炭资源与安全开采国家重点实验室，江苏 徐州，221008； 3.安徽理工大学，安徽 淮南 232001； 4.龙岩学院，福建 龙岩 364012)



瓦斯爆炸压力与波前瞬态流速演化特征及其定量关系

林柏泉1，2，洪溢都1,2，朱传杰1,2，江丙友3，刘 谦4，孙豫敏1,2

(1.中国矿业大学安全工程学院，江苏 徐州 221116； 2.煤炭资源与安全开采国家重点实验室，江苏 徐州，221008； 3.安徽理工大学，安徽 淮南 232001； 4.龙岩学院，福建 龙岩 364012)

为了建立爆炸波前的瞬态流速和超压的定量关系，采用数值模拟的方法分别研究了开口型方管内瓦斯爆炸超压和瞬态流速传播特征。研究结果表明：开口型方管内，波前瞬态流速和超压的波形曲线的峰值个数不一样，而且超压峰值总是早于波前瞬态流速峰值出现。大部分情况下，方管横截面边长越大，其超压峰值相对较小，并且超压峰值沿传播方向呈现降低趋势。波前瞬态流速峰值沿传播方向呈不断增长趋势，而且方管横截面边长越大，其峰值也相对较小。长径比(方管长度与横截面边长之比)小于125时，超压峰值与波前瞬态流速峰值的定量关系始终呈现线性反比关系；大于或等于125时，超压峰值和波前瞬态流速峰值的定量关系呈分段关系。研究结果可为爆炸冲击波扬尘的研究提供基础数据。

爆炸力学；瞬态流速；超压；瓦斯爆炸

可燃性煤尘爆炸是煤矿灾害的重要形式之一，但是单一的煤尘爆炸在煤矿中很少见，它往往由瓦斯爆炸引发，作为一种次生灾害发生。爆炸冲击波能否扬起煤尘，是发生煤与瓦斯爆炸的关键。B.Fletcher[1]通过研究发现冲击波前的高速气流是粉尘扬起的关键因素，目前这种观点已经得到学界的认可。因此，研究冲击波扬尘问题关键在于是否能够准确了解爆炸冲击波的波前流场特征。

由于当前实验条件有限，波前瞬态流速的分布特征仍然难以通过实验方法获得，目前能得到的最多的是用纹影或阴影法拍到的流场特征[2-4]。但这种方法归根结底是一种定性方法，只能配合定量测试方法来定性描述爆炸火焰或冲击波的传播特征[5-7]。考虑到爆炸波的超压是相对容易在实验室测得的参数，如果能建立爆炸波前瞬态流速与超压的定量耦合关系，对认识不同爆炸强度的扬尘能力具有重要意义。但目前很少有学者对爆炸的波前流速进行单独研究。杨书召等[8]给出了冲击波和波前流速关系的理论公式，但是该公式只适用于惰性冲击波，也难以准确估算冲击波对气体介质所做的功。

基于上述研究现状以及课题组此前所做的研究工作[9-10]，本文中研究开口型系统内的爆燃波前瞬态流速与爆炸超压的变化规律，并尝试建立两者之间的关系，为预测开口型系统内的冲击波前流场特征提供一种新的方法，从而为评估不同强度下爆炸波冲击波扬尘特征提供依据。

1 数值模型及验证

1.1 数值模型

数值模拟软件AutoReaGas能够较好地模拟气体爆炸，模拟的可靠性较高[11-13]。湍流作为气体燃烧爆炸的重要因素，采用k-ε模型。燃烧反应过程简化成基元反应，而燃烧速率Rc表示为[14]

(1)

式中：Ct是量纲一常数，ρ是密度，Γ是质量扩散系数，Rmin是可燃物、氧气和燃烧产物中的最小值。 湍流燃烧速度St表示为[15]

(2)

式中：ut湍流强度，Lt湍流的特征长度，Sl是层流燃烧速度，ν是运动黏度。数值模拟中的其余设置参数参考W.P.M.Mercx等[16]的研究设定。初始阶段的层流燃烧速率按照准层流模型处理。Fs是另外一个重要的修正系数，主要是为了修正压力、温度和火焰前沿褶皱对层流燃烧速度的影响。Sl,eff是湍流火焰速度，其与Fs、火焰半径r和理论层流火焰速度Sl的关系表示为[17]

(3)

数值计算的初始参数按参考文献[18]进行设置。

1.2 实验验证

有学者曾利用实验矿井进行了大量实验，发现只要数值模拟结果与实际实验误差值在±47%以内，数值模拟的结果就能够满足工程现场的需要[19]。C.J.Lea等[20]也通过实验证实了AutoReaGas软件模拟的可靠性。本文中通过相关实验来验证实验数据与数值结果，从而验证网格划分的合理性以及模型的合理性。

1.2.1 实验设备

实验设备如图1所示。实验管道为方形不锈钢管，管长L=5 m，横截面边长a=8 cm， 如图1(a)所示。数值模拟所建模型管道与实验管道一样。管道左端为封闭点火端，管道右端开放。图1(b)是活塞式压力计，主要用于标定传感器，尽量避免测量误差。压力测点自管道左端0.5 m开始布置，每隔0.5 m安置一个，总共9个，火焰测点安装在管道左端0.25 m处，起触发开关用，如图1(c)所示。点火能量是2 J。实验瓦斯气体体积分数为9.5%。在对比参数的选取上，采用实验方法易于获得的爆炸超压值[21]。

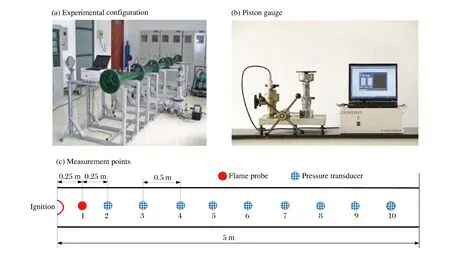
图1 实验设备Fig.1 Schematic of experimental equipment

1.2.2 实验结果与数值模拟结果对比

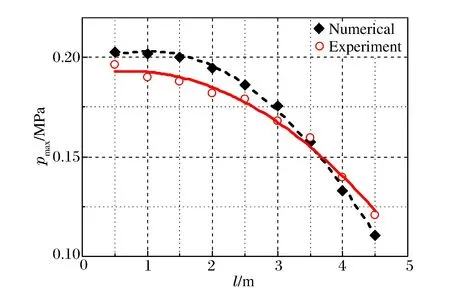
图2 管道实验数据和数值模拟结果的对比Fig.2 Comparison of numerical and experimental results

数值模拟实验中选取了2种网格进行对比选择。一种网格尺寸为2 cm×2 cm×2 cm，另一种网格尺寸为4 cm×4 cm×4 cm，模拟结果与实验结果对比如表1中所示。应该说明的是，表格中对比的数据是超压峰值pmax，测点与点火端的距离为l，数值模拟结果与管道实验数据之间的偏差程度为E。从中可以发现2 cm×2 cm×2 cm的网格划分所得的模拟结果与实际更吻合。因此用2 cm×2 cm×2 cm的网格进行更深入的模拟研究。图2为数值模拟结果与管道实验数据的对比，可以看出数值模拟结果与实验结果吻合较好。表2为数值模拟结果与管道实验数据以及两者的偏差，其中最大的偏差是8.35%，明显小于47%。因此，我们认为在这种数值模型以及这种网格划分方法下的模拟结果具有较大的可靠性。

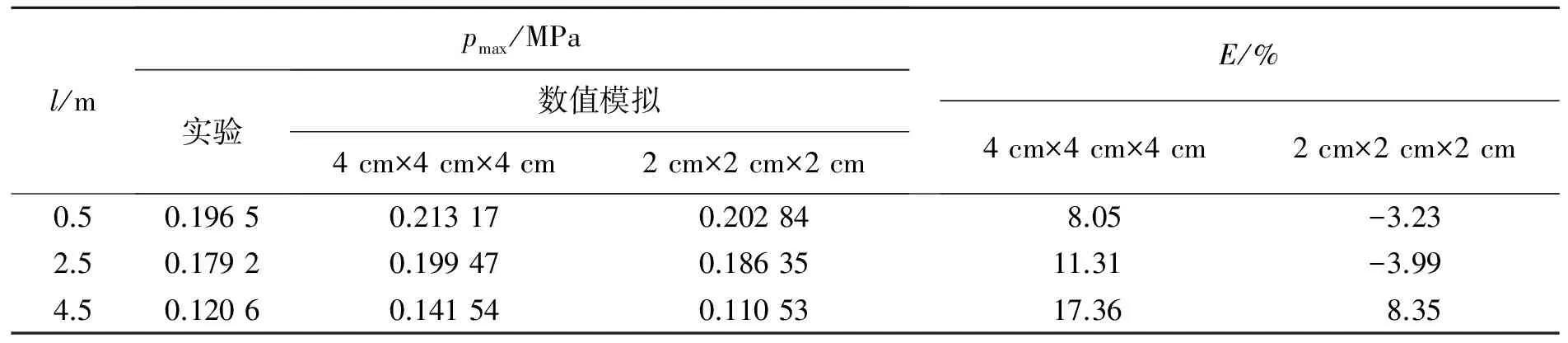
表1 不同网格划分方法下的数值模拟结果的对比

注：表中的偏差以管道实验结果为基准，其顺序与数值模拟结果的呈对应关系。

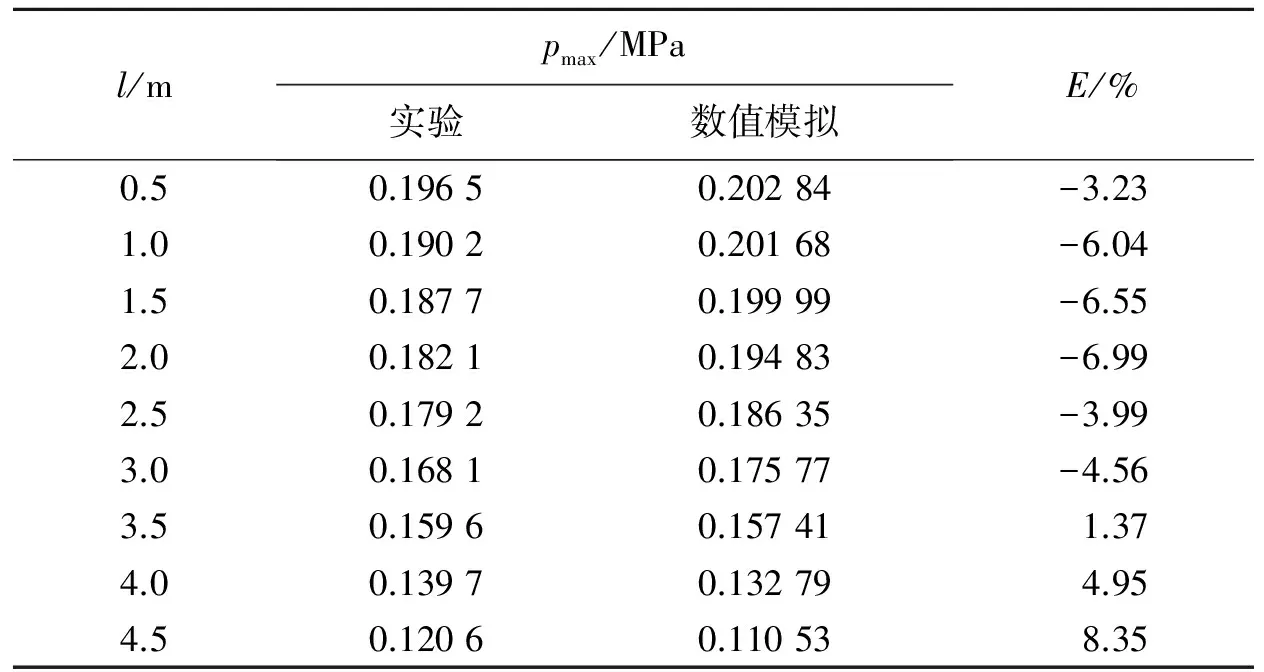
表2 数值模拟结果与实验数据的对比

2 数值计算结果与分析

2.1 超压和波前瞬态流速的变化规律

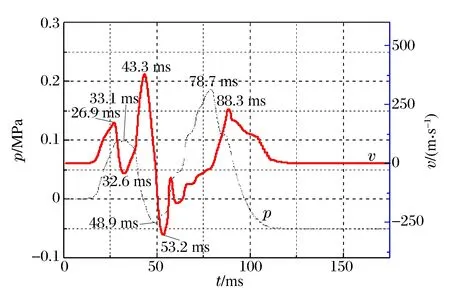
图3 超压和波前瞬态流速随时间的变化规律Fig.3 Overpressure and flow speed versus time

图3为开口型管道内的超压p和波前瞬态流速v随时间t的演化特征曲线。由于管道中火焰始终处于缓燃阶段，前驱冲击波尚未完全形成，其超压值很小，所以超压波形曲线只体现火焰锋面的影响，而波前瞬态流速演化波形曲线却表现出了前驱冲击波和火焰锋面两者的影响。因此，前驱冲击波和火焰锋面的影响下，波前瞬态流速在26.9、43.3 ms时依次出现2个正向峰值，而由于波后回流现象的影响,在32.6、53.2 ms出现2个反向峰值；然后由于封闭端的反射作用,波前瞬态流速再一次加速，在83.3 ms时出现第3个正向峰值；最后由于气体动能不断耗散，波前瞬态流速不断减速直至趋于零。比较而言，超压的演化波形曲线稍微简单一点，在33.1 ms时才出现首个正向峰值，而后不断降压，在53.2 ms时出现首个反向峰值，接着再次升压，在78.7 ms时出现第2个正向峰值，而后不断降压，直至趋于一个定值。冲击波传播过程中，在到达某处时会首先对该处的气体进行压缩，使密度、压力升高，而后由于密度增加、体积减小，流体质点被冲击波推动，这时才产生运动速度[22]。所以超压峰值总是在波前瞬态流速峰值之前出现，这在图中清晰可见。

2.2 超压峰值与波前瞬态流速峰值沿传播方向上的分布规律

图4～5为开口型管道内超压峰值pmax和波前瞬态流速峰值vmax沿传播方向的演化曲线。管道横截面边长a为8、20和30 cm等3种，管道长度L有5、10、15和20 m等4种。从图4中可以看到，L和a都能够明显影响超压峰值的变化趋势。当L相同时，a越小，超压值越大。而当a为20和30 cm，超压峰值在点火端要比管道末端大，沿传播方向上呈降低趋势。而当a为8 cm时，其变化趋势与L的值相关。5和10 m管道中超压峰值沿传播方向呈降低趋势，最小值在管道末端；但是在15和20 m管道中超压峰值却呈现先降低后增长的变化趋势，最小值在管道中间。

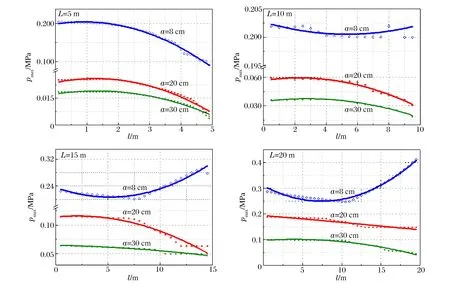
图4 管道尺寸不同时超压峰值沿传播方向的分布Fig.4 Overpressures in different tubes

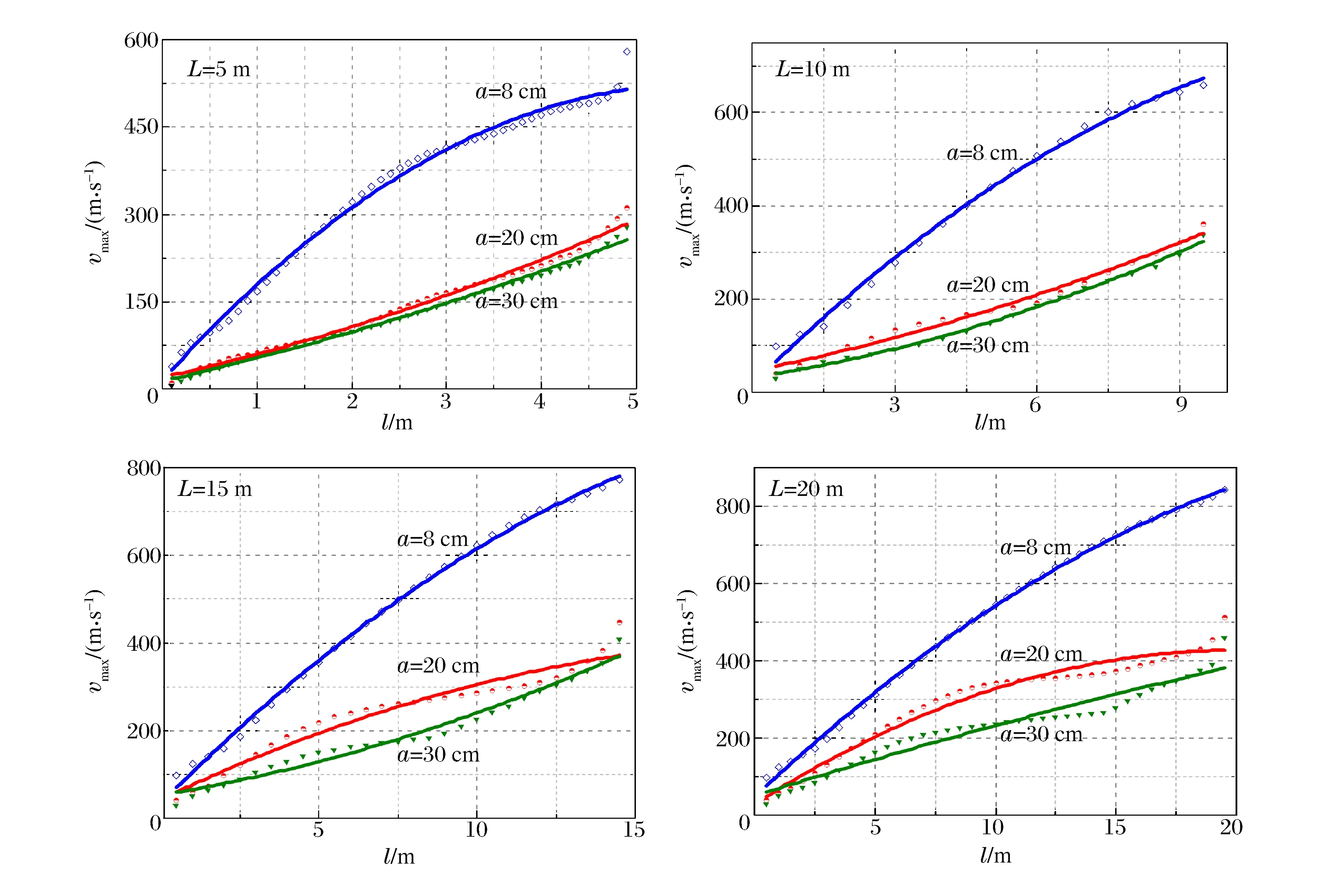
图5 不同管道尺寸中流速峰值沿传播方向的分布Fig.5 Flow velocities in different tubes

从图5中可以看出，a值对波前瞬态流速峰值的影响与对超压峰值的影响类似。a越小，流速峰值在不同管道的相同测点位置上越大。但是L的值对两者的影响却有明显的不同，当a相同时，波前瞬态流速峰值沿传播方向上只呈明显的增大趋势，而不是超压峰值的多样变化。因此，L和a的综合影响使得波前瞬态流速峰值在不同情况下有明显区别。当L为20 m、a为8 cm时，波前瞬态流速最大可达到852 m/s；而当L为5 m、a为30 cm时，波前最大流速最大才278 m/s，两者相差数倍。

2.3 超压峰值与波前瞬态流速峰值的定量关系

图6为超压峰值与波前瞬态流速峰值的定量关系。图中r为长径比，即L与a的比值。从图4～5可知，除了在a为8 cm、L为15和20 m时超压先减小后增大的情况外，当a的值相同时，波前瞬态流速沿传播方向不断增大，而超压沿传播方向不断减小。当火焰处于缓燃阶段时，气体爆炸释放的能量较小，超压和波前瞬态流速会出现此消彼长的变化；而当火焰处于爆燃阶段时，气体爆炸释放的能量足以维持超压和波前瞬态流速的同时增长[23]。所以，当r较小时，管道中的火焰始终处于缓燃阶段，超压和波前瞬态流速的耦合关系是反比关系；而当r较大时，火焰在经历过一段缓燃阶段之后会进入爆燃阶段，所以波前瞬态流速和超压的耦合关系早期是反比关系，但是到后期是正比关系，这在图6中有着直接的体现。从图中可以清晰地看出，当r<125时，超压峰值和波前瞬态流速峰值都呈单一线性反比关系；当r=125时，两者之间的定量关系开始呈分段关系，并且两段都呈线性反比关系；等到r=187.5、250时，则早期依然呈反比关系，但是后期就变为正比关系。

图7为图6中超压与波前瞬态流速耦合得到的斜率和截距。图形中左轴是截距h，右轴是斜率k，横坐标是r。当r<100时，k与r呈反比关系，如图中B所示。当r>125时，即当a=8 cm、L=15和20 m时，k与r在早期仍然呈反比关系，如图中C所示，而在后期则转换为正比关系，如图中D所示。而对于h而言，在r<100时，h与r呈正比关系，如图中A所示，但是在r>125时，h与r却都是反比关系，如图中E和F所示。

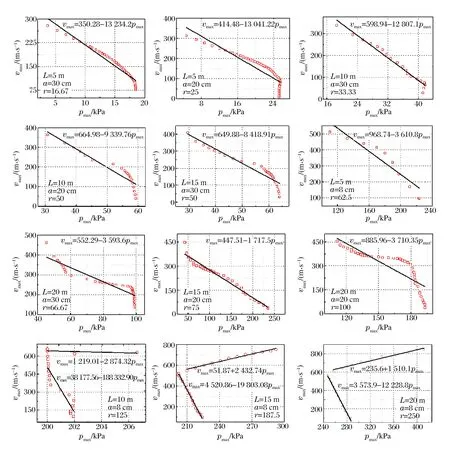
图6 超压峰值与波前瞬态流速峰值的定量关系Fig.6 Relationships between flow velocities and overpressures

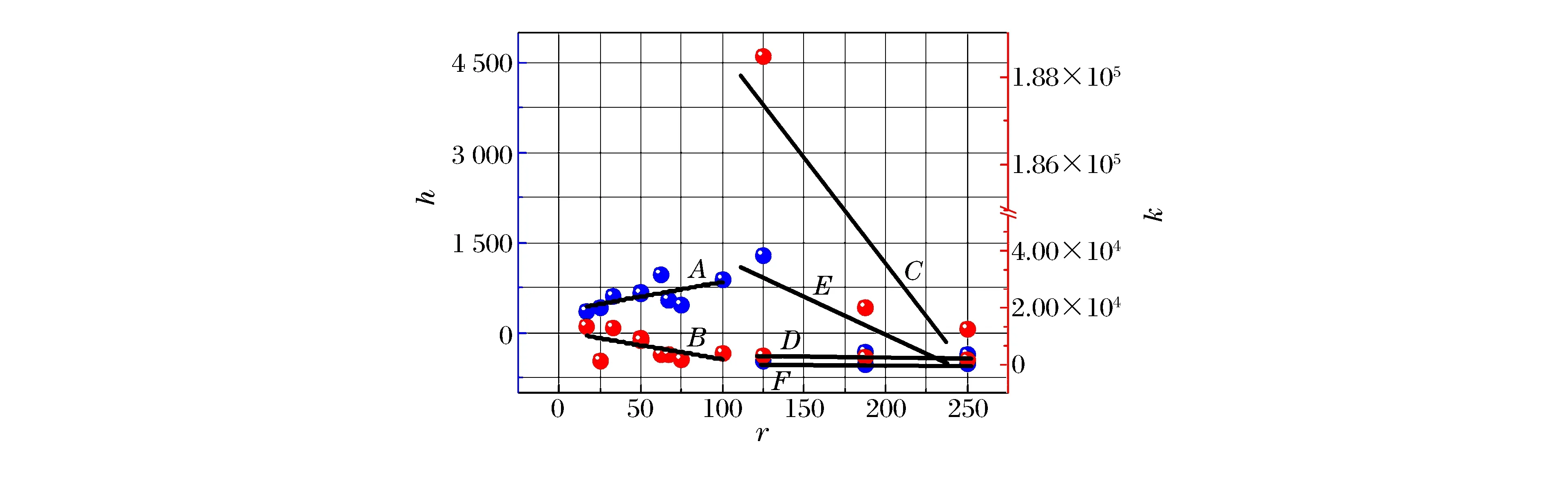
图7 斜率和截距的分布关系Fig.7 Fitting curves of slope and intercept

3 结 论

(1)开口型管道内，波前瞬态流速和超压在前驱冲击波和火焰锋面的不同影响下表现出不一样的演化波形曲线。超压演化波形曲线只有2个正向峰值和1个反向峰值，而波前瞬态流速演化波形曲线却有3个正向峰值和2个反向峰值。此外，超压峰值总是早于波前瞬态流速峰值出现。

(2)管道长度L和管道横截面边长a对超压峰值和流速峰值都有明显影响。a值较大的管道，其超压峰值比a值较小管道中的超压峰值小，而且在a值较大管道中超压峰值的降低趋势要比a值较小管道中的降低趋势更为平缓，同时超压峰值沿传播方向上呈降低趋势。但是当a=8 cm、L=15和20 m的管道中，超压峰值沿传播方向上表现出先下降后上升的变化趋势。波前瞬态流速峰值在a值较大的管道中比a值较小的管道中要小，而且其沿传播方向上呈增长趋势。

(3)在对超压峰值和流速峰值的定量关系分析中发现，当长径比小于125时，超压峰值和波前瞬态流速峰值的定量关系始终呈单一线性反比关系；当长径比是125时，两者之间的定量关系开始呈分段关系，并且两段都呈线性反比关系；等到长径比为187.5和250时，则定量关系早期依然呈反比关系，但是后期就变为正比关系。

[1] Fletcher B. The interaction of a shock with a dust deposit[J]. Journal of Physics, D: Applied Physics, 1976,9(2):197-202.

[2] Kuznetsov M, Alekseev V, Matsukov I, et al. DDT in a smooth tube filled with a hydrogen-oxygen mixture[J]. Shock Waves, 2005,14(3):205-215.

[3] Ilbas M, Crayford A P, Ylmaz I, et al. Laminar-burning velocities of hydrogen-air and hydrogen-methane-air mixtures: An experimental study[J]. International Journal of Hydrogen Energy, 2006,31(12):1768-1779.

[4] Johansen C T, Ciccarelli G. Visualization of the unburned gas flow field ahead of an accelerating flame in an obstructed square channel[J]. Combustion and Flame, 2009,156(2):405-416.

[5] Ciccarelli G, Johansen C T, Parravani M. The role of shock-flame interactions on flame acceleration in an obstacle laden channel[J]. Combustion and Flame, 2010,157(11):2125-2136.

[6] Ciccarelli G, Johansen C T, Parravani M. The role of shock-flame interactions on flame acceleration in an obstacle laden channel[J]. Combustion and Flame, 2010,157(11):2125-2136.

[7] Ciccarelli G, Dorofeev S. Flame acceleration and transition to detonation in ducts[J]. Progress in Energy and Combustion Science, 2008,34(4):499-550.

[8] 杨书召,景国勋,贾智伟.矿井瓦斯爆炸冲击气流伤害研究[J].煤炭学报,2009,34(10):1354-1358. Yang Shu-zhao, Jing Guo-xun, Jia Zhi-wei. Injury study on impact current of gas explosion in coal mine[J]. Journal of China Coal Society, 2009,34(10):1354-1358.

[9] Zhu C J, Lin B Q, Hong Y D, et al. Numerical simulations on relationships between gas velocity and overpressure of gas explosions in ducts[J]. Disaster Advances, 2013,6(S1):217-227.

[10] Lin B Q, Hong Y D, Zhu C J, et al. Effect of length on the relationships between the gas velocity and peak overpressure of gas explosion disasters in closed-end pipes[J]. Disaster Advances, 2013,6(S2):176-184.

[11] Jiang B Y, Lin B Q, Shi S L, et al. A numerical simulation of the influence initial temperature has on the propagation characteristics of, and safe distance from, a gas explosion[J]. International Journal of Mining Science and Technology, 2012,22(3):307-310.

[12] Maremonti M, Russo G, Salzano E, et al. Numerical simulation of gas explosions in linked vessels[J]. Journal of Loss Prevention in the Process Industries, 1999,12(3):189-194.

[13] Pang L, Zhang Q, Wang T, et al. Influence of laneway support spacing on methane/air explosion shock wave[J]. Safety Science, 2012,50(1):83-89.

[14] Janovsky B, Selesovsky P, Horkel J, et al. Vented confined explosions in Stramberk experimental mine and AutoReaGas simulation[J]. Journal of Loss Prevention in the Process Industries, 2006,19(2):280-287.

[15] Bray K N C. Studies of the turbulent burning velocity[J]. Proceedings of the Royal Society of London. Series A: Mathematical and Physical Sciences, 1990,431(1882):315-335.

[16] Mercx W P M, Van den Berg A C, Hayhurst C J, et al. Developments in vapour cloud explosion blast modeling[J]. Journal of Hazardous Materials, 2000,71(1):301-319.

[17] Bakke J R. Numerical simulation of gas explosions in two-dimensional geometries[J]. Christian Michelsen Institute, 1986:865403-865408.

[18] AutoReaGas user manual version 3.1[Z]. England: Century Dynamics and TNO, 2002.

[19] Zipf R K, Sapko M J, Brune J F. Explosion pressure design criteria for new seals in US coal mines[S]. 2007.

[20] Lea C J, Ledin H S. A review of the state-of-the-art in gas explosion modelling[M]. Health and Safety Laboratory, 2002.

[21] Salzano E, Marra F S, Russo G, et al. Numerical simulation of turbulent gas flames in tubes[J]. Journal of Hazardous Materials, 2002,95(3):233-247.

[22] 吴望一.流体力学(下册)[M].北京:北京大学出版社,2011:414-432.

[23] Baker W E, Cox P A, Kulesz J J, et al. Explosion hazards and evaluation[M]. Access Online via Elsevier, 1983.

(责任编辑 曾月蓉)

Quantitative relationship between flow speed and overpressure of gas explosion in the open-end square tube

Lin Bai-quan1,2, Hong Yi-du1,2, Zhu Chuan-jie1,2, Jiang Bing-you3, Liu Qian4, Sun Yu-min1,2

(1.FacultyofSafetyEngineering,ChinaUniversityofMiningandTechnology,Xuzhou, 221116Jiangsu,China; 2.StateKeyLaboratoryofCoalResourcesandSafeMining,Xuzhou221008,Jiangsu,China; 3.SchoolofMiningandSafetyEngineering,AnhuiUniversityofScienceandTechnology,Huainan232001,Anhui,China; 4.SchoolofResourceEngineering,LongyanUniversity,Longyan364012,Fujian,China)

The main objective of this study is to establish the quantitative relationship between overpressure and flow speed in the open-end square tube by the numerical simulation. It is found that the numbers of the peak value of overpressure and flow speed at the same measured point are different. The peak overpressure always appears earlier than peak flow speed in time scale. In mast cases, larger side lenth of square tube corresponds to smaller peak overpressure, and the peak flow speed goes down slowly along the propagation direction. The peak overpressure decreases with the increasing of the distance far from ignition end. However, the peak flow speed increases with the stream wise distance. When normalized distance is less than 125, the peak overpressure and peak flow speed always presents an inverse relationship. Otherwise, the relationship is piecewise-linear. The results may provide reference for the study on evaluating the dust lifting ability behind shock wave in the limited spaces.

mechanics of explosion; flow speed; overpressure; gas explosion

10.11883/1001-1455(2015)01-0108-08

2013-04-25；

2013-11-13

国家重点基础研究发展计划(973计划)项目(2011CB201205)；国家自然科学基金青年科学基金项目(51204174)；中国矿业大学人才引进&青年教师启航计划(2011RC07)；中央高校基本科研业务费专项基金项目(2012QNB01)

林柏泉(1960— )，男，博士，教授,lbq21405@126.com。

O389；TD712.7 国标学科代码： 13035

A