小型高压引爆装置冲击电流简易测量方法

陈 祎，袁士伟，吴 昊，王 鹏，林润山

(北京航空航天大学宇航学院，北京 100191)



小型高压引爆装置冲击电流简易测量方法

陈 祎，袁士伟，吴 昊，王 鹏，林润山

(北京航空航天大学宇航学院，北京 100191)

依据脉冲放电电路的等效电路及其微分方程，采用Levenberg-Marquarat算法对主电容放电电压测试波形数据进行衰减系数识别，从而获得模拟电流波形。该方法克服了分流器法和Rogowski线圈法等直接测量小型高压引爆装置冲击电流时，因附加电路引起的电流波形失真。MATLAB模拟结果表明，该方法得到的电流模拟波形与真实电流波形拟合精度高，可用于直列式引信电子安全与解除保险装置和低能冲击片雷管的优化匹配设计。

爆炸力学；Levenberg-Marquarat算法；放电电流模拟；小型高压引爆装置；衰减系数

高压引爆装置冲击电流的测量普遍采用的方法是分流器法和Rogowski线圈法[1]。分流器是能产生与施加电流成比例的电压信号的电阻器。分流器法原理简单，但需将分流器接入脉冲放电回路的闭合路径中，对于微小型高压引爆装置，分流器本身的剩余电感对原始电路参数有较大改变，当脉冲上升很快时，分流器的感抗加大，使测得电流波形与实际电路电流波形有较大误差。Rogowski线圈是能产生与输入电流成比例的输出信号的电流互感器[2]。其优点是被测信号与被测回路没有联系，是一种非接触测量装置，但对于微小型高压引爆装置，线圈的体积过大，无法使被测回路穿过线圈，只能在放电回路中接入一段导线，但导线的接入同样改变了原始回路的电感参数，导致测得的电流波形误差较大。

本文中针对微小型高压引爆装置无法通过分流器法或Rogowski线圈法等常规方法获得实际产品状态下精确冲击电流波形的现状，依据主电容放电电流方程与放电电压方程的关系，采用Levenberg-Marquarat算法对主电容放电电压测试波形数据进行衰减系数识别，间接获得电流波形参数，进而得到模拟电流波形。通过同一状态下实测电压波形获得的模拟电流波形与实测电流波形的对比，证明此方法的有效性。

1 数学物理模型

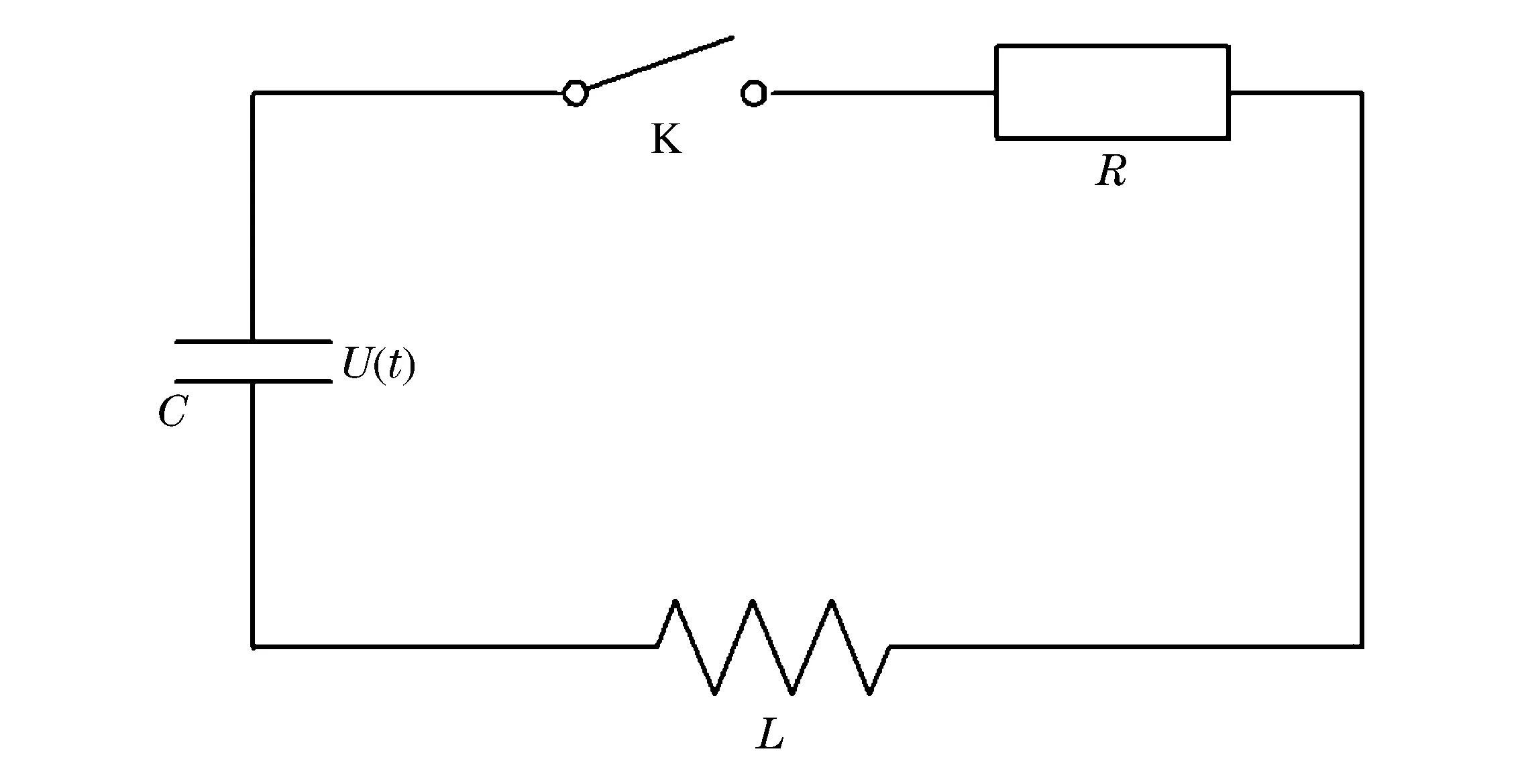
图1 高压引爆装置放电回路示意图Fig.1 Discharge circuit of high-voltage exploding device

高压引爆装置放电回路可简化为如图1所示的等效RLC串联电路。图中K为触发管开关，R为回路总电阻，L为回路总电感，C为电容器电容。容器充电电压为U0，触发管开关K被触发而导通时，电容器放电，电路中形成脉冲电流I(t)，电容器两端电压为U(t)。假设：(1)触发管开关K为理想开关，导通电阻并入回路电阻R中；(2)电容器选定，忽略电容器内电抗对放电电流的影响。

根据图中所示的放电回路，由基尔霍夫定律可得到

(1)

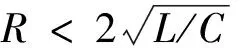
(2)

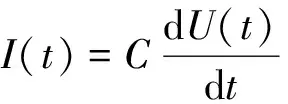
(3)

(4)

式中：δ为衰减系数，ω为实际电流波形的角频率，f为电流频率，T为电流周期。

2 衰减系数识别算法

2.1 衰减系数识别的最小二乘问题

经过上一节的推导，建立了电容器放电电压U(t)与待识别衰减系数δ之间的非线性模型，可以采用非线性最小二乘法识别参数。

设有m组观测数据(ti,Ui)(i=1,…,m)，作偏差平方和函数

(5)

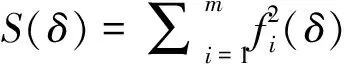
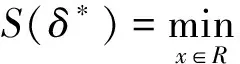
2.2Levenberg-Marquarat识别算法

非线性最小二乘问题的解算方法主要分为3大类：(1)近似解法，当非线性模型的非线性强度较弱，可以将非线性模型在初始点处线性化，再用线性模型的求解方法来解算。(2)数值迭代解法，从初始点出发，确定迭代方向和步长，重复进行迭代直至满足收敛准则。数值迭代法包括牛顿法、梯度法、信赖域法等[3-4]。(3)其他算法，一般是指直接搜索算法，如单纯形法、遗传算法、神经网络算法。

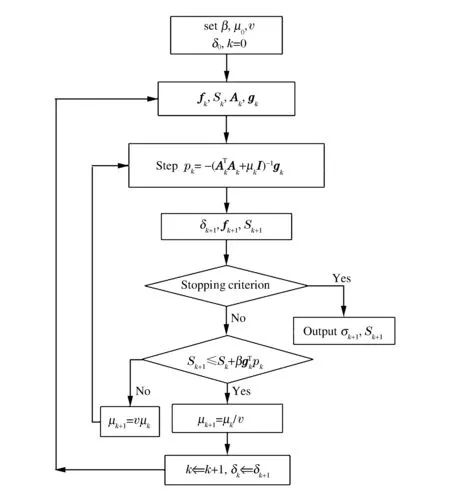
图2 衰减系数识别流程图Fig.2 Attenuation coefficient identification flowchart

对于当前迭代点，L-M算法的迭代步长为[8]

(6)

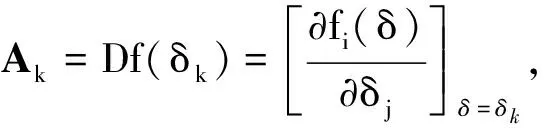
综上所述，衰减系数识别算法可总结为图2所示的流程图。

3 数据处理及波形模拟分析

3.1 数据处理流程及实验参数选取

实际的高压引爆装置放电回路衰减系数的识别采用如下的流程：放电回路进行短路放电，利用高压探头测量电容器两端放电电压并送入示波器；在示波器中，将电压波形以Excel格式转存入计算机；在计算机中，用MATLAB实现识别算法，在程序开始时读入*.xls波形数据文件，导入各采样点的ti、Ui值，注意：电压值还须乘以高压探头的变换系数，才是真实的电压值；最后将通过程序运算识别出的衰减系数δ*带入电流表达式(3)中，在MATLAB中生成模拟电流波形。

放电电压表达式(2)中，电容两端充电电压U0通过高压探头测得；参数C由脉冲放电回路的储能电容决定，其电容量可以用电桥精确测定；周期T由示波器于电压波形中读取并进行多次放电取平均值。

在实际的衰减系数识别过程中，发现选取电压负半轴波形的数据或者包括负半轴波形的数据进行识别，得到的电流模拟波形拟合效果不好，仿真波形幅值较实测波形小。原因可能是冷阴极开关管反向导通时的导通特性变差，内阻非线性增长，导致电压波形斜率变小，使用负半轴数据识别出来的衰减系数变大，模拟出来的电流波形幅值变小。由于微小型高压引爆装置与低能冲击片雷管设计优化主要集中在电流的第1峰值，在实验中发现第1峰值在电压波形正半轴四分之一周期内产生。为保证参数识别效果，在数据的采用上只选用电压波形前四分之一的波形数据，这样既保证了模拟结果的准确性，又与冲击片雷管的实际工作过程相符。

3.2 算例识别结果与波形模拟

将一个∅35 mm×10 mm(体积约10 cm3)微小型高压引爆装置接入一段5 cm长的导线并串入Rogowski线圈，对其放电回路进行放电实验，电容器放电电压波形如图3所示。在程序中利用电压波形对衰减系数进行识别，将结果带入电流表达式(3)中并在MATLAB中生成模拟电流波形。测试放电回路的实验参数为电容器充电电压U0=1 900 V，电容器电容C=0.098 μF。

程序运行结果如表1所示，从表中可以看出，步长pk在结果距离最优值较远时逐渐增大以提高迭代速度，当接近最优值时步长变小以提高迭代精度。程序迭代至最终步，S(δ)已经趋近于零，一阶最优性P趋近于零表示δ*趋近于最优值。最终得到衰减系数的最优值为δ*=2.293 5×106。

将衰减系数的最优值带入电流表达式(3)中，在MATLAB中生成电流模拟波形。电流模拟波形与Rogowski线圈测得波形的对比图如图4所示，冲击电流波形第1峰值为1 738 A，电流从零到第1峰值上升前沿时间为110 ns。由图3～4可见，放电电压与电流均呈现衰减震荡的状态，并周期性地改变方向，电容器也周期性地充放电。电流极值点在电压斜率最大时产生，电流过零点在电压极值点附近产生。表2为电流模拟波形与实测波形拟合结果，表中E为相对误差。从波形对比图及拟合结果表中可以看出：根据L-M算法识别结果重建的波形与实测波形拟合较好，证明了识别算法的有效性。

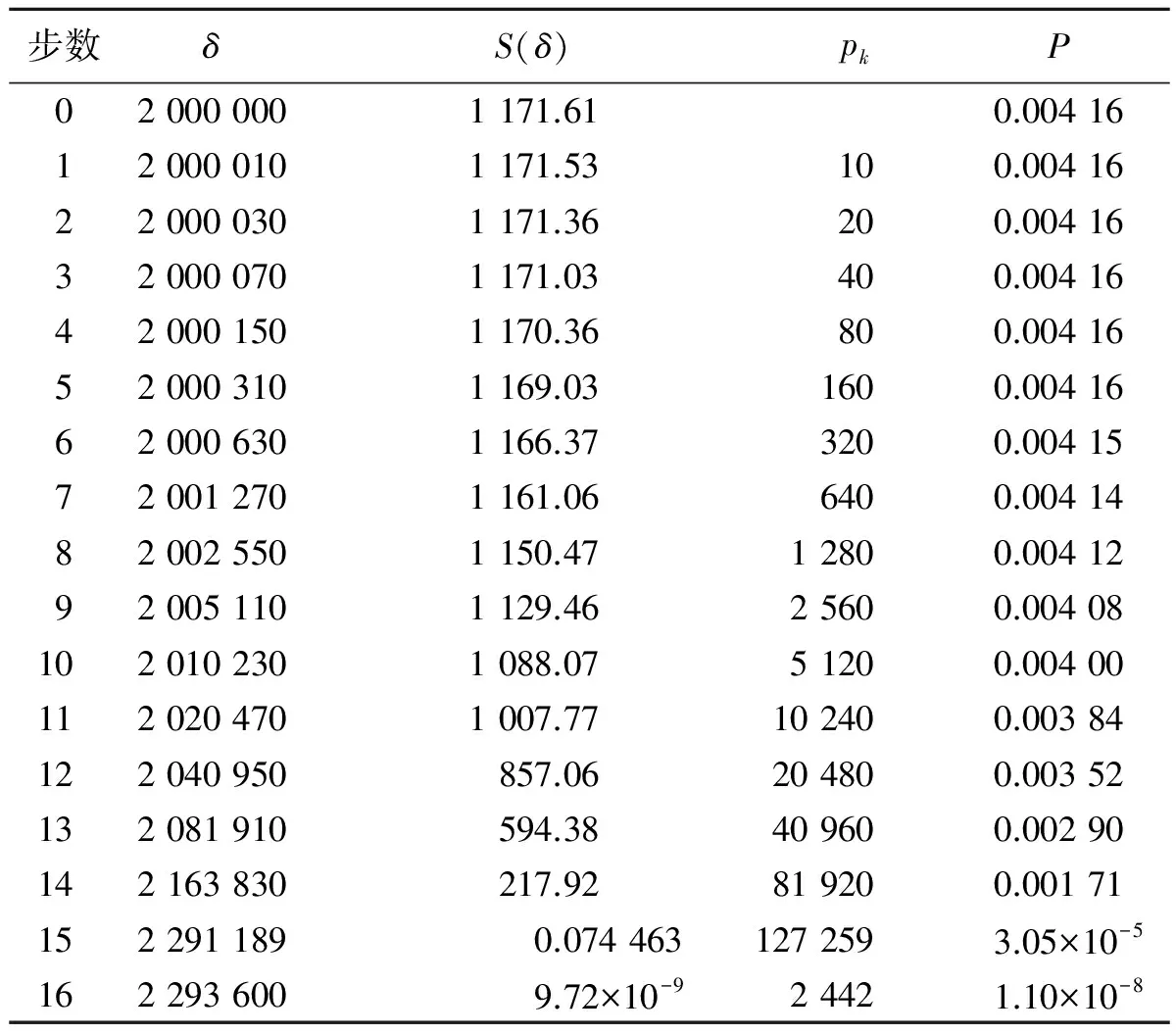
表1 衰减系数识别数值结果

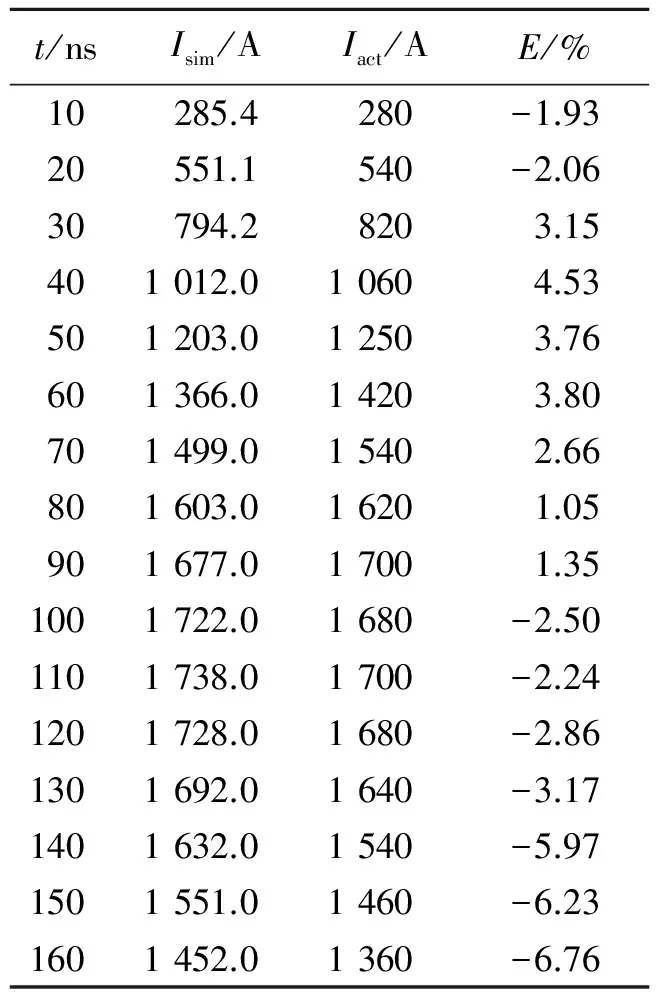
表2 模拟波形与实测波形拟合结果表

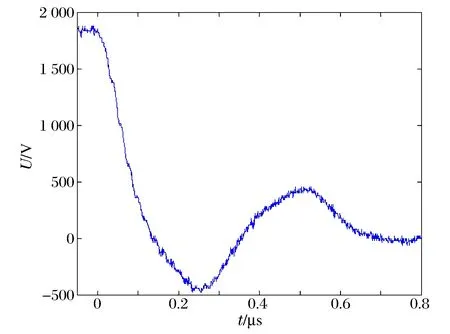
图3 电容器放电电压波形Fig.3 Waveform of capacitance discharge voltage

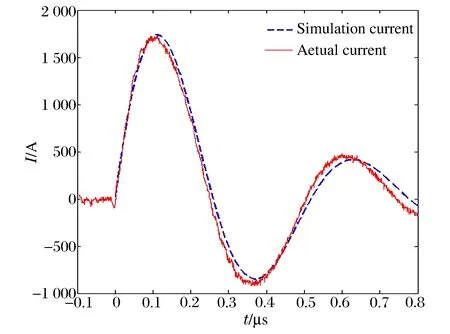
图4 模拟电流波形与实测波形对比图Fig.4 Waveforms of simulation current and measured current

4 结 论

识别与模拟结果表明，采用基于L-M算法的识别方法能有效地实现对衰减系数的识别。在对电压波形数据进行处理时，利用真实电压波形初始四分之一周期的数据进行处理，识别精确度高。利用该方法可以根据放电电压的真实曲线模拟出该放电回路的放电电流波形。为高压引爆装置进一步小型化，以及直列式引信电子安全与解除保险装置与低能冲击片雷管的优化匹配设计提供了设计工具。

[1] 陈景亮,姚学玲,孙伟.脉冲电流技术[M].西安：西安交通大学出版社,2008.

[2] 戴建华,李开成.基于Rogowski线圈的大电流测量[J].高电压技术,2002,28(1):6-10. Dai Jian-hua, Li Kai-cheng. Heavy current measurement based on Rogowski coil[J]. High Voltage Engineering, 2002,28(1):6-10.

[3] Eriksson J, Wedin P A, Gulliksson M E. Regularization methods for uniformly rank-deficient nonlinear least-squares problems[J]. Journal of Optimization Theory and Applications, 2005,127(1):1-26.

[4] Zhang J Z, Xue Y, Zhang K. A structured secant method based on a new quasi-newton equation for nonlinear least squares problems[J]. Bit Numerical Mathematics, 2003,43(1):217-229.

[5] 邹志伟.求解对称非线性方程组的一种修正共轭梯度法[D].长沙：湖南大学,2010.

[6] 孙风建.基于新拟牛顿方程的非线性最小二乘的一类新算法[D].南京：南京理工大学，2007.

[7] Fan Jin-yan. The modified Levenberg-Marquardt method for nonlinear equations with cubic convergence[J]. Mathematics of Computation, 2011,81(277):447-466.

[8] 王新洲.非线性模型参数估计理论与应用[M].武汉:武汉大学出版社,2002.

(责任编辑 曾月蓉)

A simple method of measuring impulse current of small high-voltage exploding device

Chen Yi， Yuan Shi-wei， Wu Hao， Wang Peng， Lin Run-shan

(SchoolofAstronautics，BeiHangUniversity，Beijing100191，China)

A simple method was developed for measuring the impulse current waveform produce by a small high-voltage exploding device. The model of impulse current was determined by attenuation coefficient. To estimate the attenuation coefficient from the actual discharge voltage curve, the Levenberg-Marquarat algorithm was applied based on the equivalent circuit of discharge circuit and its differential equations. Compared with the direct measuring methods such as using shunt or Rogowski coil, this method overcomes the distortion of impulse current waveform caused by additional measuring circuit. The results show that the simulation current waveform fits the actual current waveform well. The method can be used for optimum matching design of electronic safety, arming device of in-line fuse or low-energy slapper detonator.

mechanics of explosion; Levenberg-Marquarat algorithm; impulse current simulation; small high-voltage exploding device; attenuation coefficient

10.11883/1001-1455(2015)01-0065-05

2013-05-02；

2013-07-15

陈 祎(1989— )，男，硕士研究生,tonychenyc@gmail.com。

O389；TJ431 国标学科代码： 13035

A