利用导数巧解一类常见的三角函数问题

徐振宇 陈贤婵 郭小瑞

（陕西师范大学数学与信息科学学院）

在三角函数的教学和练习中, 师生常常会碰到一类这样的三角函数问题：

问题1：（2013 浙江镇海中学阶段性测试）已知3sinα+4cosα=5，求tanα。

师生通常是从三角方面的知识与方程方面的知识相结合出发进行求解，但有时对于像问题1、问题2 师生可以将三角方面的知识与导数求极值的知识相结合来巧妙解答。因为三角函数相关的知识学习是在必修内容中，而导数相关知识在选修内容中，在高中数学的教学过程中，很多学校老师往往是先进行必修内容的教学，再进行选修内容的教学。选修内容的有些知识与前面必修内容知识联系密切。比如，导数与函数会放在高三复习时连接起来，但是因为高考对三角函数的考查一般很少与导数联系起来，所以很多师生都会忽略导数与三角函数相结合起来解题。有时对于像问题1、2 这种类似的问题，将导数与三角函数结合起来能巧妙快速准确地解答题目。

作者先给出问题1 目前常见的四种解法。

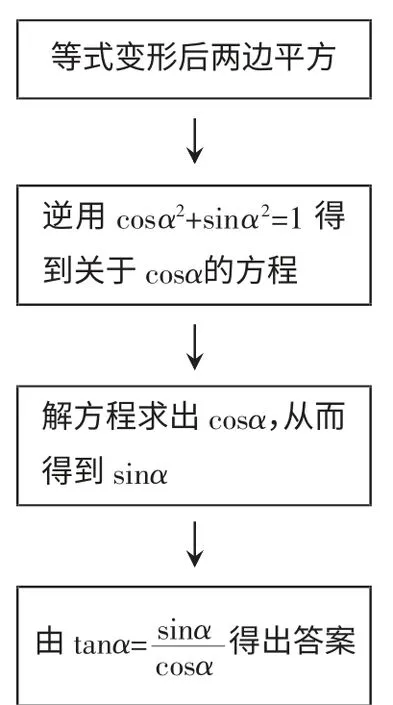
图1 思路1

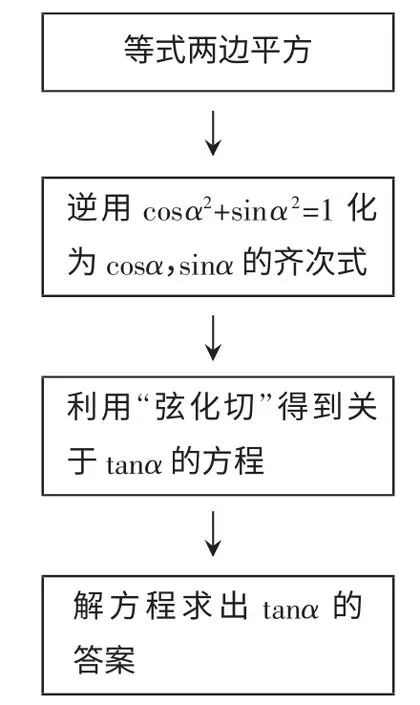
图2 思路2

解法1：

3sinα+4cosα=5，等式变形得3sinα=5-4cosα，两边平方得9sin2α=25-40cosα+16cos2α

得到关于cosα 的方程：25cos2α-40cosα+16=0，

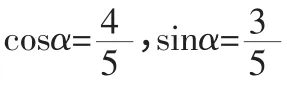
解法2：

等式两边平方得到：

9sin2α+24sinαcosα+16cos2α=25

9sin2α+24sinαcosα+16cos2α=25（sin2α+cos2α）

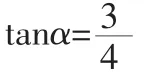
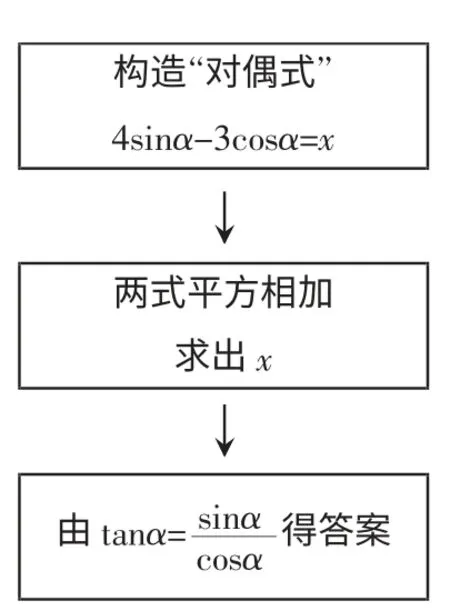
图3 思路3

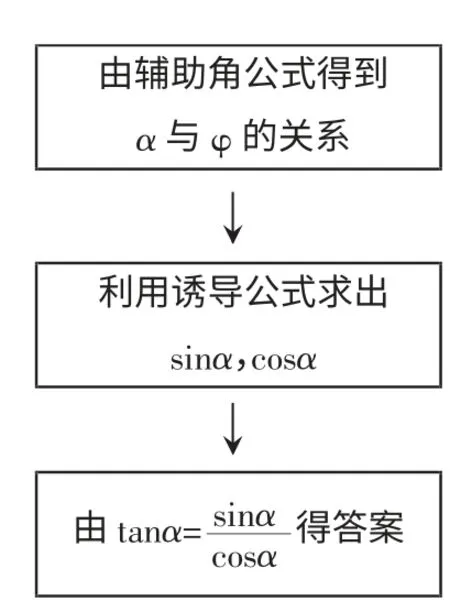
图4 思路4

解法3：

设4sinα-3cosα=x，两式平方相加得到

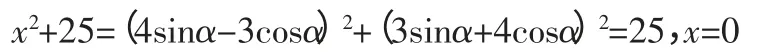
解法4：

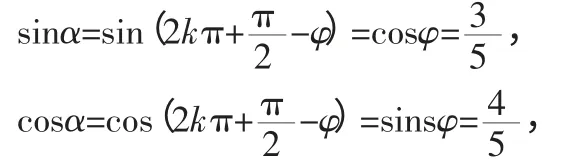
现在，重点介绍解法5：利用导数的有关知识来求解。

解法5：

设f（x）=3sinx+4cosx，

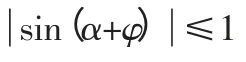
∴f（a）的最大值为5，最小值为-5，

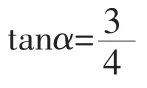
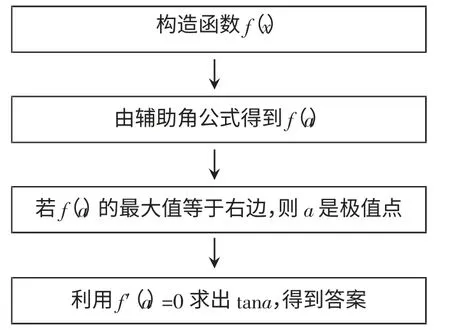
图5 思路5

作者在用解法5 给学生讲解这类题时，效果是非常好的。因为在用前面的方法讲解时，学生虽然入手很快，但是总在计算时出错，得分率不是很高，但是教授了解法5 后，学生出错的概率小了很多，除了个别求导求错之外。将此法写出来与大家分享，希望能给同仁以帮助与启示。