基于区间分析的汽车制动器不确定性优化*

吕 辉,于德介

(湖南大学,汽车车身先进设计制造国家重点实验室，长沙 410082)



2015140

基于区间分析的汽车制动器不确定性优化*

吕 辉,于德介

(湖南大学,汽车车身先进设计制造国家重点实验室，长沙 410082)

为抑制不确定参数汽车制动器的制动噪声，基于区间分析理论，将响应面法与优化技术相结合，提出了一种降低系统复模态负阻尼比以提高汽车制动器稳定性的优化方法。该方法采用拉丁超立方试验设计在设计变量和不确定参数构成的混合空间内采样，建立了包含不确定参数的制动器系统复模态负阻尼比的响应面近似模型；以系统结构参数为设计变量，以最小化系统复模态负阻尼比为优化目标，利用基于区间分析的不确定性优化方法对响应面近似模型进行优化。对某型车的浮钳盘式制动器的优化结果表明，采用该方法对汽车制动器进行优化，能在整个使用周期内有效减小制动器不稳定模态的负阻尼比，从而提高制动器的稳定性。

制动噪声;不确定性;区间分析;优化

前言

汽车制动噪声已成为城市的主要噪声污染源之一。如果汽车的制动器设计不合理，制动时就可能引起强烈的振动，并产生刺耳的噪声。由于在设计后期，制动器产品的结构形状、尺寸和工艺已确定，修改设计空间的自由度已大大减小，因此在早期设计中，有必要对制动器部件的结构参数进行合理的匹配设计，以抑制制动噪声，提高整车NVH性能。

目前被国内外大多数学者所认可的制动噪声机理为系统自激振动理论，根据该理论，制动噪声是由摩擦耦合和制动器各部件模态参数匹配不当而产生的自激振动所引起的[1]，即制动噪声与摩擦材料特性和结构的具体形式有关。多年来，国内外学者在制动噪声控制方面做了大量研究工作。文献[2]中在建立制动器动力学模型的基础上，用最优化方法对结构动态特性进行修改，抑制了产生尖叫噪声的不稳定模态。该研究对制动器的设计有一定的指导意义，但研究对象仅为制动器支撑支架，而单部件优化抑制噪声的方法在应用上存在一定的局限性。文献[3]中建立了盘式制动器系统的耦合模型，针对系统几何参数和材料特性参数的一系列取值，分别求解了制动器的复模态，提出了降低摩擦因数和修改制动片几何形状的制动噪声抑制方法。该研究的主要特点是从复模态负阻尼比的角度进行分析，各部件参数独立研究，得到的结果只是一个噪声产生倾向的定性说明。实际上，为充分考虑各部件间的相互耦合关系，有效控制制动噪声，应对整个制动器系统建立优化模型，并对多部件参数同时进行优化设计。

国内现有的关于制动噪声的研究，多数是基于确定性的力学模型，即将结构参数和作用载荷视为确定参数[4]。而汽车制动器由于长期承受摩擦力等复杂载荷的作用，其材料特性、几何尺寸和作用载荷等参数往往具有不确定性，尤其是不断磨损会引起制动片的厚度尺寸变化。为了使设计得到的优化解能更好地满足工程实际要求，应在优化设计时考虑不确定因素的影响。对于不确定性问题，大多采用概率方法，把不确定变量作为随机变量处理，但在工程实际中有时很难提供充分的概率分布信息来描述这些随机变量，因而限制了基于概率的优化方法在工程中的应用[5-6]。基于区间分析的不确定性优化方法把不确定参数看作区间数，只须获得参数的上下界信息即可，这些信息在工程实际中也很容易获得，因此基于区间分析的优化研究在工程中得到了广泛的应用[7]。

本文中针对汽车制动噪声的抑制问题，将响应面法与优化技术相结合，对具有不确定参数的汽车制动器进行区间分析优化研究，提出了一种基于区间分析的汽车制动器不确定性优化方法。该方法首先采用拉丁超立方试验方法在不确定参数和设计变量所构成的混合空间内进行试验设计；再建立包含区间参数的制动器系统复模态负阻尼比的响应面近似模型；最后以结构几何参数为设计变量，以减小系统复模态负阻尼比为优化目标，利用基于区间分析的不确定性优化方法对响应面近似模型进行优化，以提高制动器的稳定性。对某型车的浮钳盘式制动器的分析和优化结果表明，采用该方法对汽车制动器进行优化，能有效减小制动器不稳定模态的负阻尼比，从而提高了制动器的稳定性。

1 汽车制动器噪声的预测原理

文献[8]的研究表明，制动器工作时，系统引入了摩擦力，导致系统为一个耦合系统，其运动方程可以表示为

(1)

式中：M，C，K分别为无摩擦制动器系统的质量矩阵、阻尼矩阵和刚度矩阵；μ为摩擦因数；Kf为摩擦接触刚度矩阵；D为振动位移向量。

由式(1)可知，由于摩擦力的存在导致了系统刚度耦合，系统的刚度矩阵不对称。从数学角度来看，刚度矩阵不对称意味着特征矩阵不对称，而不对称矩阵的特征值在一定条件下是复数。

式(1)的特征方程为

det(s2M+sC+K+μKf)=0

(2)

式中s为系统复特征值，记为

s=a±jb

(3)

式中：a为特征值的实部，是系统的阻尼系数；b为特征值的虚部，是系统的自然频率。由系统控制理论知，一个系统为稳定系统的充分必要条件为：系统的特征值具有负实部。因此a的正负决定了一个系统的稳定与否。

定义复特征值的阻尼比[3]为

(4)

式中ζ为系统复特征值的阻尼比。如果阻尼比为正，即a<0，则系统是一个衰减振动系统，系统是稳定的；如果阻尼比为负，即a>0，则系统随着时间推移而放大振动，系统是一个不稳定系统。因此根据制动器系统复特征值的阻尼比来判断其稳定性。阻尼比值的大小与系统的稳定程度相关，负阻尼比绝对值越大则制动器系统越不稳定，产生噪声的可能性越大。

因此，在制动器摩擦耦合系统中，具有正实部的特征值对应的模态是不稳定模态，表现为有噪声倾向的模态。如果采用有限元分析方法求出制动器的复模态和对应的阻尼比，就能对制动噪声倾向进行预测。本文中以表征系统稳定程度的复模态的负阻尼比为目标函数。

2 汽车制动器的不确定性近似模型

2.1 汽车制动器不确定性因素分析

汽车制动器是由多个部件组成的系统，以盘式制动器为研究对象，主要的部件有制动盘、制动片、支撑背板、绝缘板、卡钳、分泵和油管等。存在于系统部件中的不确定性因素与制动噪声的产生有着密切的关系。主要的不确定性因素如下。

(1) 摩擦因数的不确定性 为了方便，多数研究都把制动盘和制动片之间的摩擦因数简化成一个恒定的数值[4]。虽然目前国内外对制动噪声的产生机理还未能达成共识，但研究表明：摩擦因数-相对滑动速度曲线的负斜率是产生制动噪声的主要因素之一[9]。摩擦因数在实际工况中并不是恒定的，受温度、压力、湿度和粉尘等因素的影响，摩擦因数会在一定范围内波动，因此在优化设计中应考虑摩擦因数不确定性的影响。本文中将摩擦因数不确定取值区间定在初始值的±10%范围之内。

(2) 制动压力的不确定性 对于盘式制动器，两个制动片分别装在制动盘的两侧，分泵的活塞受油管输送来的液压作用，推动制动片挤压转动中的制动盘，由此产生摩擦阻力而达到减速效果。制动主缸和油路的变化，制动卡钳所受摩擦力的变动以及分泵活塞密封性的变化等都会引起制动压力在一定范围的波动性。本文中将制动压力不确定取值区间定在初始值的±10%范围之内。

(3) 制动片磨损的不确定性 制动片作为制动器的主要部件之一，对制动器的振动和噪声有着重要影响。相对其它部件，制动片是一个易损件，随着车辆的使用，制动片会不断磨损。已有研究表明，随着制动片的磨损，制动器系统的耦合摩擦特性会发生变化，导致出现一些只在磨损状态下产生的振动或噪声。因此在制动器的早期设计中必须考虑到制动片的整个使用寿命周期，针对其整个厚度变化过程进行优化设计，而不是只针对某一个确定的厚度值。制动片一般磨损到只剩原来厚度的1/3时进行更换，本文中根据该使用原则及其初始厚度确定其取值范围。

(4) 制动盘磨损的不确定性 制动盘相对制动片来说其磨损是相当微小的，属于非易损件，故暂不考虑其磨损情况。

2.2 响应面近似模型

由于对制动器系统模型进行数值计算的时间较长，基于该模型的优化计算，特别是进行嵌套优化计算，每次计算响应值都要调用有限元模型，导致计算效率低下，阻碍了优化算法在制动器系统优化设计中的应用。用近似模型代替真实模型的设计方法，是目前解决大规模抽象模型优化问题的有效方法，可大幅度提高工程优化问题的求解效率。

建立近似模型的基本原理是通过数理统计和试验设计的方法，建立设计变量和响应值之间的函数关系，用以代替复杂的真实模型。本文中选用响应面法在指定的采样空间内进行有限次数的试验设计，以输出变量的全局逼近来代替真实响应。

假定系统响应与设计变量之间满足函数关系：

y=g(x1,x2,…,xn)

(5)

式中：y为系统响应；x1,x2,…,xn为n个设计变量。通过试验设计，系统响应与设计变量确定的函数关系为

y=f(x1,x2,…,xn)

(6)

式中f(x1,x2,…,xn)是对g(x1,x2,…,xn)的近似，其表示的曲面为响应面。

多项式响应面是应用比较广泛的一种近似模型，它具有数学表达式较为简单，且易于实现等特点。工程中通常采用二次多项式响应面近似模型，其基本形式为

(7)

式中：c0，ci，cii和cij为待确定的未知系数；n为设计变量个数。

2.3 试验设计

为了建立有效的近似模型，须借助试验设计的方法，以获取足够多且合适的样本点。采样点的选择不当会导致近似模型的精度低、甚至错误，并且会提高构建近似模型的成本。本文中采用拉丁超立方试验设计方法[10]进行抽样。其采样点在采样空间中分布均匀，可以在相对较少的采样次数下，获得充分的信息。因为基于区间分析的不确定性优化的目标函数是设计变量和不确定性变量的函数，所以采样空间应由设计变量和不确定性变量组成。

2.4 汽车制动器噪声预测的不确定性近似模型

为减少计算量，同时又能真实准确地模拟制动器的振动特性，利用Altair. Hypermesh软件建立了某型轿车的制动器有限元模型，如图1所示。

该模型由制动盘、制动片、支撑背板和绝缘板4部分组成，共有26 125个实体单元，37 043个节点，其中六面体单元(C3D8)25 041个，五面体单元(C3D6)1 084个，制动片与制动盘之间为摩擦接触面，整个系统为一个摩擦耦合系统，各部件材料特性参数见表1。该模型的制动片前期已经过中部开槽和边缘倒圆角等工艺处理，噪声倾向性已较小，但还不能完全消除。将定义好边界条件和工况的有限元模型提交ABQUS/Standard即可求解系统的复模态和阻尼比。

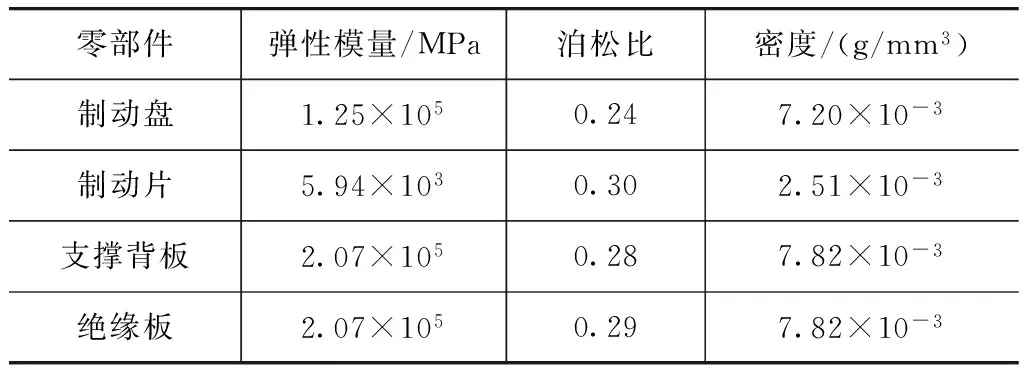
表1 制动器部件材料参数

文献[3]中的研究表明，在盘式制动器系统中，摩擦因数、制动压力、制动盘转速、制动盘刚度、制动片刚度和支撑背板刚度这些设计参数都与系统的不稳定模态有关，但制动盘转速和制动压力对不稳定模态的影响极小，因此选取制动盘刚度和制动片刚度参数为设计变量，选取摩擦因数、制动压力和制动片刚度参数为不确定性变量。其中制动片、制动盘和支撑背板的刚度特性分别通过其几何厚度参数间接体现。

根据制动器部件的规格和不确定特性，制动器设计变量和不确定参数的初始值和取值范围如表2所示。采用拉丁超立方试验设计方法，选取了35组由摩擦因数μ、制动压力p、制动片厚度h1、制动盘厚度h2和支撑背板厚度h3组成的样本点。

将试验设计中得到的35组样本点代入到制动器系统有限元模型中进行计算，得出其相应的不稳定模态及其负阻尼比。通过有限元计算，发现系统对应各组样本点的第6，7阶模态均为复模态，其中第7阶模态的复特征值实部大于0，为不稳定模态；

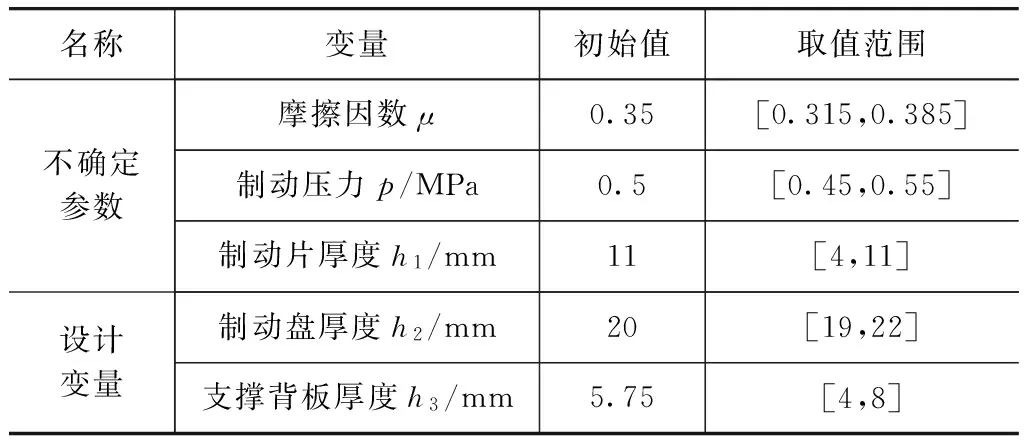
表2 试验设计采样空间

个别样本点还在其它阶数上出现复模态，但其复特征值的负阻尼比值都远比第7阶模态的负阻尼比值小；因此本文中主要对第7阶模态进行研究。初始状态下，制动器的第6，7阶模态的复特征值分别为-97.088+1962.2j和97.088+1962.2j。第7阶复模态的负阻尼比为-0.015 75，振型图如图2所示。

以第7阶复模态为研究对象，根据第2.2节的方法，建立以摩擦因数μ、制动压力p、制动片厚度h1、制动盘厚度h2和支撑背板厚度h3为自变量的制动器系统负阻尼比的近似模型。基于2阶多项式响应面模型建立的负阻尼比的近似表达式为

ζ(μ,p,h1,h2,h3)=-0.0463-0.2046μ+

0.0598p+0.0004h1+0.0101h2-0.0138h3-

0.2431μp+0.0038μh1-0.0023μh2+0.0169μh3-

0.0293ph1+0.0159ph2+0.0028ph3-0.0007h1h2+

0.0005h1h3+0.0004h2h3+0.3908μ2+0.0159p2+

(8)

根据文献[10]中的方法对上述响应面模型进行显著性分析，由F检验结果知响应面模型的不可靠概率小于1%，与真实有限元模型的逼近程度高，能够较好地满足预测精度要求。

3 基于区间分析的不确定优化理论

基于区间分析的系统不确定性优化问题，一般可表述为

(9)

式中：f为包含设计变量和不确定参数的目标函数；gi为第i个不确定约束函数；k为不确定约束的个数；X为n维设计向量；U为不确定向量；上标L和H表示区间的下界和上界。

利用区间数理论中的区间序关系对区间进行比较，则式(9)的不确定优化问题可转化为式(10)的多目标优化问题：

(10)

式中：m(f(X,U))为目标函数区间的中点；ω(f(X,U))为目标函数区间的半径；fL(X)和fH(X)分别由式(11)得出：

(11)

至此，通过区间序关系转换，将式(9)的不确定优化问题转化为式(10)的多目标确定性优化问题。为方便后续求解，采用线性加权法将式(10)进一步转化为一单目标优化问题：

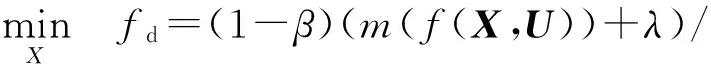
β(ω(f(X,U))+λ)/ψ

(12)

式中：fd为单目标评价函数；β为权重系数，其取值范围为0≤β≤1；λ为保证m(f(X,U))+λ和ω(f(X,U))+λ非负的常数；φ和ψ为各目标函数的正则化因子：

(13)

实际应用中，上述两个参数可以根据具体问题，大致取与各自目标同一量级的值即可，以防止“大数吃小数”的现象发生。

本文中采用罚函数方法来处理不确定优化问题的约束条件，使其转化为单目标无约束优化问题，式(12)可写为

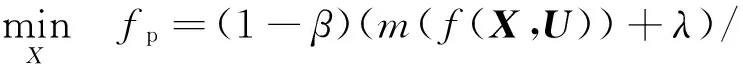
β(ω(f(X,U))+λ)/ψ+

(14)

式中：σ为惩罚因子，通常取一个较大的值，当不满足约束条件时将受到惩罚，使搜索保持在可行域内。

4 基于区间分析的制动器不确定性优化

制动器系统不确定优化的目的是使制动器在其整个使用寿命周期中不稳定模态的负阻尼比尽可能小，从而提高制动器系统的稳定性，降低制动噪声产生的可能性。本文中以第2.4节的盘式制动器系统为研究对象，以式(8)表述的不稳定模态的负阻尼比ζ(μ,p,h1,h2,h3)为目标函数，以设计变量取值范围为约束条件，得到制动器系统的不确定优化问题的数学模型：

(15)

在区间不确定性优化方法中，将区间中点和区间半径视为同等重要，则式(14)中权重系数β=0.5。取参数λ=0.1，则式(15)最终可表示为

(16)

其中

(17)

采用隔代遗传算法对上述目标函数进行优化。隔代遗传算法是在微型遗传算法的基础上加入隔代映射算子。隔代映射算子是用来沿着连续两代中最好个体的方向上，寻找更好的个体，以代替当前代中最差的个体[11]。隔代遗传算法不仅继承了微型遗传算法种群规模小、基因多样性和全局优化的特点，而且提高了收敛速率。

首先，外层遗传算法在制动盘厚度h2和支撑背板厚度h3组成的设计空间内寻优，对于每个所取的设计向量进入内层遗传算法，在不确定摩擦因数μ、制动压力p、制动片厚度h1组成的不确定参数空间内搜索，通过计算响应面近似模型ζ(μ,p,h1,h2,h3)确定目标函数响应的上下界，进而得到目标函数响应区间的中点和半径。把内层优化结果反馈给外层优化算法，以帮助外层算法继续寻优，直到满足停止准则输出最后的设计变量作为优化结果。整个优化流程如图3所示。

最后的优化结果为，在不确定参数作用下，当h2=21.8mm，h3=7.5mm时，制动器系统不稳定模态的负阻尼比区间为[-0.015 3,-0.003 7]，不确定区间中心为-0.009 5，区间半径为0.005 8。以区间中点来说，优化后的负阻尼比值比优化前降低了39.7%，即使为最不利情况，即负阻尼比为-0.015 3，也比优化前降低了2.9%。

将优化后的结果h2=21.8mm，h3=7.5mm以及不确定参数的一组初始取值：μ=0.35，p=0.5MPa，h1=11mm代入有限元模型分析计算，结果显示第7阶模态复特征值为69.736+2029j，负阻尼比为-0.010945，在优化结果区间内，振型如图4所示，并且除了第7阶模态外，其余全部均为稳定模态，制动器系统整体稳定性大幅提高。

5 结论

(1) 在参数不确定性的基础上，结合区间分析理论，将响应面法与优化技术相结合，应用遗传算法，对汽车制动器系统进行优化。该方法在对制动器系统设计参数进行寻优的同时，还考虑了实际工况部分参数的不确定性，从而使设计得到的优化解能更好地满足工程实际要求。

(2) 对某型车的浮钳盘式制动器的分析和优化结果表明：采用该方法对汽车制动器进行优化，能有效提高优化设计结果的稳健性，使制动器在其整个使用寿命周期中不稳定模态的负阻尼比尽可能小，从而提高制动器的稳定性，减小制动噪声产生的可能性。

[1] 管迪华,宿新东.制动振动噪声研究的回顾、发展与评述[J].工程力学,2004,21(4):150-155.

[2] 宿新东,管迪华.利用子结构动态特性优化设计抑制制动器尖叫[J].汽车工程,2003,25(2):167-170.

[3] Liu P, Zheng H, Cai C, et al. Analysis of Disc Brake Squeal Using the Complex Eigenvalue Method[J]. Applied Acoustics,2007,68(6):603-615.

[4] 吕辉,于德介,谢展,等.基于响应面法的汽车盘式制动器稳定性优化设计[J].机械工程学报,2013,49(9):55-60.

[5] Cho G M. Log-barrier Method for Two-stage Quadratic Stochastic Programming[J]. Applied Mathematics and Computation,2005,164(1):45-69.

[6] Sengupta A, Pal T K, Chakraborty D. Interpretation of Inequality Constraints Involving Interval Coefficients and a Solution to Interval Linear Programming[J]. Fuzzy Sets and Systems,2001,119:129-138.

[7] Jiang C, Han X, Guan F J, et al. An Uncertain Structural Optimization Method Based on Nonlinear Interval Number Programming and Interval Analysis Method[J]. Engineering Structures,2007,29(11):3168-3177.

[8] Mario T J , Samir N Y G, Roberto J. Analysis of Brake Squeal Noise Using the Finite Element Method[J]. Applied Acoustics,2008(69):147-162.

[9] Kinkaid N M, O’Reilly O M, Papadopoulos P. Automotive Disc Brake Squeal[J]. Journal of Sound and Vibration,2003,267(1):105-166.

[10] Papilla M. Accuracy of Response Surface Approximations for Weight Equations Based on Structural Optimization[D]. University of Florida,2001:43-48.

[11] 刘桂萍,韩旭,姜潮.并行隔代映射遗传算法及其在材料参数反演中的应用[J].中国机械工程,2007,18(4):387-390.

Uncertainty Optimization of Vehicle Brakes Based on Interval Analysis

Lü Hui & Yu Dejie

HunanUniversity,StateKeyLaboratoryofAdvancedDesignandManufacturingforVehicleBody,Changsha410082

To suppress the noise of vehicle brakes with uncertain parameters, an optimization scheme by reducing the negative damping ratio of the complex mode of brake system to improve the brake stability is presented based on the theory of interval analysis and combining response surface method with optimization technique. The scheme adopts the Latin hypercube design of experiment to conduct sampling within the mixed space formed by design variables and uncertain parameters and create a response surface approximation model for the negative damping ratio of the complex mode of brake system with uncertain parameters. With the structural parameters of brake system as design variables and minimizing the negative damping ratio of its complex mode as optimization objective, an optimization is performed on response surface approximation model with an uncertainty optimization scheme based on interval analysis. The results of the optimization on the float caliper disc brake of a vehicle show that the optimization on vehicle brakes using the scheme presented can effectively reduce the negative damping ratio of unstable mode of brake system in entire life cycle, and hence improve the stability of brakes.

brake noise; uncertainty; interval analysis; optimization

*湖南省研究生科研创新项目(CX2013B143)，湖南大学汽车车身先进设计制造国家重点实验室自主课题(71375004)和长沙市科技计划重大专项(K1306007-11-1)资助。

原稿收到日期为2012年9月17日，修改稿收到日期为2015年6月15日。