最优预瞄加速度驾驶员模型参数试验辨识方法研究*

白 艳，贾 鑫

(1.长安大学汽车学院，西安 710064； 2.吉林大学，汽车仿真与控制国家重点实验室，长春 130025)



2015137

最优预瞄加速度驾驶员模型参数试验辨识方法研究*

白 艳，贾 鑫

(1.长安大学汽车学院，西安 710064； 2.吉林大学，汽车仿真与控制国家重点实验室，长春 130025)

研究通过试验辨识获得最优预瞄加速度驾驶员模型物理参数的方法。采用时域辨识方法确定模型传递函数，采用非线性最小二乘法确定传递函数中所包含的物理参数，利用已知目标函数优化预瞄时间和反应时间，针对仿真数据进行了辨识分析。结果表明，该方法对驾驶员模型物理参数的辨识具有良好的效果。

驾驶员模型；最优预瞄加速度；参数辨识

前言

从20世纪50年代开始，驾驶员模型成为各国学者的研究对象，随着对驾驶员心理和生理等操纵特性认识的不断深入，驾驶员模型的精度越来越高。驾驶员模型在汽车主动安全、交通事故分析、车辆动力学分析和智能驾驶方面得到了广泛应用[1]。然而，模型中参数的获得是其使用的一个难点，是模型完备性的重要条件。驾驶员模型参数的获取必须在正常驾驶过程中进行，并且很难通过物理仪器测量，通过系统辨识方法可从驾驶过程中的数据信息中提取建模需要的参数。文献[2]和文献[3]中通过递推最小二乘法在线辨识驾驶员模型参数设计自适应转向控制主动安全系统。文献[4]中为了研究驾驶员模型参数的不确定性和未建模的动力学部分的不确定性，采用ARMAX参数辨识的方法对12名驾驶员的119组试验数据进行模型参数辨识。如果模型考虑不周全，辨识得到的参数在预测转向盘转角输出时误差也会较大[5-6]。文献[7]中用神经网络的方法对高速公路上纵向驾驶员行为模式进行识别。

文献[8]中通过测量人-飞机闭环回路中输入和输出信号的各类交叉谱密度，采用频域拟线性法估计驾驶员模型的传递函数。其等效驾驶员模型框图如图1所示，其中，Yp(s)为驾驶员模型，n(t)为驾驶员模型和真实驾驶员操作之间的误差，r(t)为预期跟随输入。驾驶员模型的传递函数可以由下式得到：

(1)

式中：φru(iω)为输入输出信号的交叉谱；φre(iω)为r(t)和e(t)的交叉谱。通过阻尼最小二乘迭代求解结构驾驶员模型参数向量[9]。

对于基于MPC和LQR方法的驾驶员模型的辨识,需要辨识的参数是其价值函数的加权系数qy和qθ[10-11]。通过比较驾驶员模型和真实驾驶员的转向盘转角输出,用迭代的方法(包括噪声模型)最小化预测误差,辨识出基于MPC方法的驾驶员模型的增益和滞后，再计算出驾驶员模型中价值函数的加权系数。

本文中所辨识的对象为郭孔辉院士1983年提出的最优预瞄加速度驾驶员模型[12]，该模型的提出是基于驾驶员的操作行为要使预瞄路径和实际跟踪路径误差最小化。该模型具有结构简单，各参数物理意义明确的特点。

1 最优预瞄加速度驾驶员模型

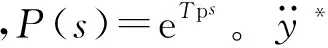
(2)

式中：Gay为汽车稳态增益；Ty1，Ty2，T1和T2为系统时间常数。

最优预瞄加速度驾驶员模型基于预瞄跟随理论，即认为预瞄环节和跟随环节的乘积为1，即

F(s)=1/P(s)

(3)

由闭环控制理论计算可得

(4)

则

(5)

对式(5)进行泰勒展开，并且保留前两项，得

(6)

设C(s)=C0(1+Tcs)

(7)

得

C0≈1/Gay

(8)

Tc≈Td+Tn+T1-Ty1

(9)

2 最优预瞄加速度驾驶员模型参数识别

表1列出最优预瞄加速度驾驶员模型中所涉及的参数及其符号。其中由式(8)可知，C0和车辆参数有关，不需辨识；Tc包括车辆参数和驾驶员模型参数Td和Tn，如Td和Tn辨识出来，则Tc不需辨识。故待辨识参数共计3个(Tp,Td和Tn)。综上所述，模型待辨识参数较少，便于辨识，并且参数意义明确。

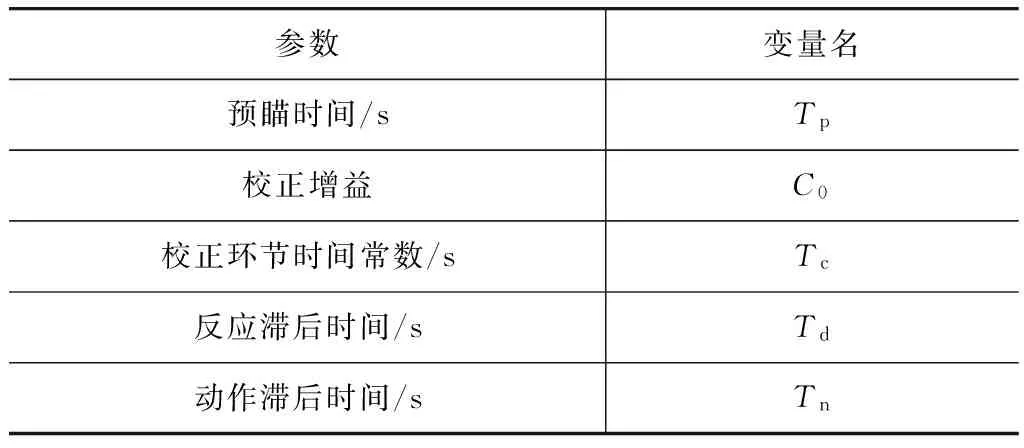
表1 最优预瞄加速度驾驶员模型参数

2.1 最优预瞄加速度驾驶员模型传递函数辨识

对于图2所示最优预瞄加速度驾驶员模型，汽车的侧向位移y(t)、预期轨迹f(t)和驾驶员转向盘转角输出δ(t)可在试验中测量得到，并可作为辨识的输入和输出数据。因此，最优预瞄加速度驾驶员模型可等价变换为图3所示的双输入单输出系统。

如图3所示，如果f(t)为辨识输入的预期轨迹，y(t)为测量车辆侧向位移，δ(t)为测量转向盘转角，则双输入单输出模型表达式为

δ(s)=f(s)Hf(s)+y(s)Hy(s)

(10)

式中：Hf为转向盘转角对预期行驶轨迹的传递函数；Hy为转向盘转角对汽车侧向位移的传递函数，即

(11)

(12)

其中

(13)

(14)

令

(15)

(16)

式中：βf0，βf1，α1，βy0，βy1和βy2均为传递函数系数。

由于驾驶员心理、生理、环境和测量因素等的影响使测量所得系统输入输出数据带有随机扰动，如转向盘转角、汽车状态测量量中所包含的测量噪声，因此，测量数据具有强噪声，而且驾驶员的随机扰动不是白噪声。常采用最小二乘法对式(15)和式(16)进行辨识[13]。

2.2 最优预瞄加速度驾驶员模型物理参数识别

由辨识可获得系统在各频率点上的频响特性，还需估计传递函数式(13)和式(14)中包含的最优预瞄加速度驾驶员模型参数Tn。可以通过在给定频率点下，寻找一组物理参数使用这组物理参数估计得到的频响特性和试验得到的频响特性式(15)和式(16)误差最小。在频率点ω，由物理参数估计的频率响应G*(jω)与辨识得到的频率响应G(jω)的误差记作：

ε(jω)=G*(jω)-G(jω)

(17)

优化目标函数为

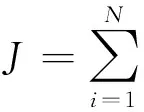
(18)

这类辨识常采用非线性最小二乘法[14]，它具有良好的迭代收敛范围和收敛速度，可用于求解非线性方程组，将非线性最小二乘问题逐次化为一系列线性最小二乘问题来迭代求解，从而减少了将非线性函数模型线性化过程中的模型误差。因此，本文中采用非线性最小二乘法优化模型中的物理参数。

2.3 预瞄时间Tp和反应时间Td的优选估计

根据驾驶员进行转向操纵的假设[15]：在驾驶安全和自身生理限制的条件下,驾驶员操纵力求使汽车实际行驶轨迹与期望路径的误差最小。根据这一假设所确定目标函数[16]为

J=Je+JSW+JLatac

(19)

其中

(20)

(21)

(22)

式中：J为闭环性能指标(目标函数)；Je为侧向位移偏差的性能指标；Jsw为转向盘转角总方差；JLatac为侧向加速度总方差；T为试验时间，s；D1，D2和D3分别为对应指标的门槛值，对于大于该值的响应值具有“惩罚作用”，取值为D1=0.5m,D2=360°,D3=3m/s2。

最后驾驶员模型物理参数组(Tp,Td,Tn,C0,Tc)应能使目标函数式(19)最小。因此，在式(11)和式(12)中，最优预瞄加速度驾驶员模型参数中的预瞄时间Tp和反应时间Td依目标函数值优选而得。

2.4 最优预瞄驾驶员模型物理参数辨识流程

最优预瞄驾驶员模型物理参数辨识步骤如图4所示。(1)生成一系列滞后时间点阵(Tp,Td)；(2)在给定滞后时间(Tp,Td)下，采用最小二乘法辨识双输入单输出系统传递函数式(15)和式(16)；(3)计算各采样频率处幅值和相角；(4)采用非线性最小二乘法拟合式(13)和式(14)所包含的物理参数Tn；(5)把滞后时间(Tp,Td)和步骤(4)中参数估计值Tn，以及Tc和C0代入人-车闭环模型(图3)中进行仿真，并计算目标函数式(19)；(6)重复步骤(2)和(3)直到估计完成(1)中所有点阵(Tp,Td)对应的辨识程序，并选择目标函数式(19)最小时对应的参数(Tp,Td,Tn)即为辨识所得参数。

3 最优预瞄加速度驾驶员模型辨识仿真结果

仿真模型的建立在Matlab/Simulink环境下生成，车辆模型为2自由度车辆模型，即

(23)

式中：Fyf=afKf；Fyr=arKr；m为汽车质量；ay为侧向加速度；v为汽车前进速度；r为横摆角速度；Fyf和Fyr分别为地面作用在前后轮的侧向力；af和ar分别为前后轮侧偏角；Kf和Kr分别为前后轴侧偏刚度；Iz为汽车绕z轴转动惯量；lf和lr分别为汽车前后轴距质心的距离。

表2为仿真时采用的车辆模型和驾驶员模型仿真参数。辨识试验采取ISO标准[17-18]中急剧移线行驶试验，其道路中心线如图5所示。图中：S1=15m；S2=30m；S3=25m；S4=25m；S5=15m；S6=15m；b为汽车宽度。

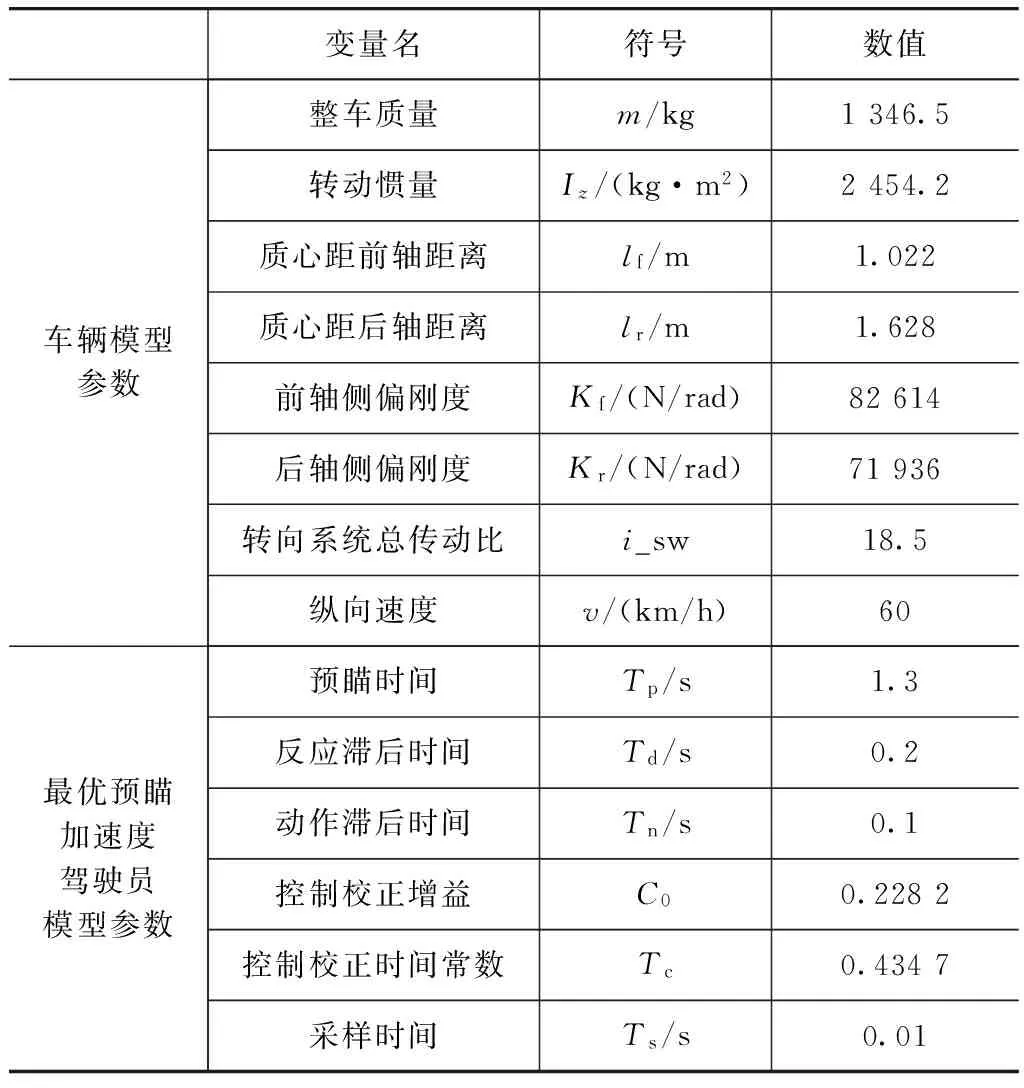
表2 车辆模型和驾驶员模型仿真参数

试验记录转向盘转角时间历程、预期道路侧向位移时间历程和跟随道路侧向位移时间历程。

图6所示为仿真所得待辨识输入输出数据，即辨识输入的预期轨迹f(t)，车辆侧向位移y(t)和转向盘转角δ(t)。

根据表2所示参数计算得到最优预瞄加速度驾驶员双输入单输出模型中传递函数为

(24)

(25)

3.2 最优预瞄加速度驾驶员模型辨识结果

在仿真中，设置Tp=1.3s,Td=0.2s和Tn=0.1s。根据文献[19]，预瞄时间Tp的取值范围为0.8～1.5s，反应时间Td的取值范围为0.2～0.6s。按照此范围形成的点阵如表3所示。按照图4所示，选取其中一组(Tp,Td)点阵，通过最小二乘法获得传递函数表达式，在通过非线性最小二乘法拟合驾驶员模型的物理参数，将拟合的参数(C0,Tn,Tc)及(Tp,Td)代入式(19)目标函数计算其值。表4为目标函数J的计算结果，表5为对应点阵辨识得到Tn值。从表4可见，当Tp=1.3s，Td=0.2s时，J最小，此时从表5可见，辨识所得Tn=0.078 9s，辨识结果与真实值比较接近。

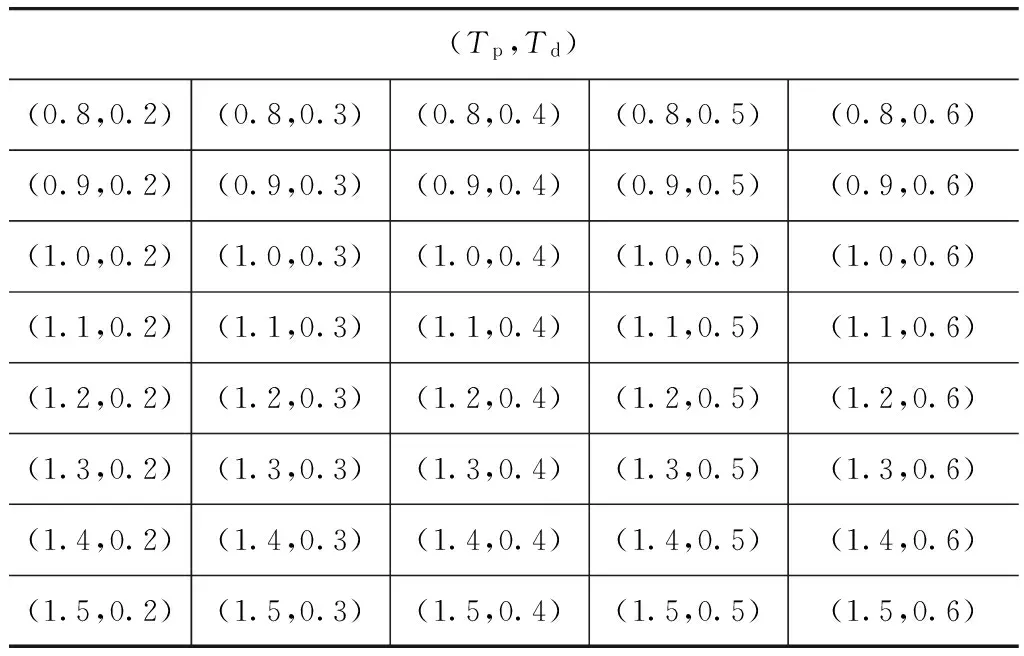
表3 (Tp,Td)点阵 s

图7为辨识环节中，实际的Hy(s)、Hf(s)的频响特性与步骤(2)辨识所得频响特性，步骤(6)所得频响特性的对比结果，其中选择表4中J=0.172 2的“结果1”和J=0.171 9(J最小)的“结果2”进行比较。由表4和表5可知，“结果1”辨识结果为Tp=1.3s，Td=0.3s，Tn=0.024 9s；“结果2”辨识结果为Tp=1.3s，Td=0.2s，Tn=0.078 9s。从图中可见，“结果1”频响特性的相频比“结果2”的相频在低频处要好，而“结果2”的幅值则比“结果1”好很多，但总体上，“结果2”的频响特性比“结果1”的频响特性要好。对于“结果2”直接辨识所得传递函数(即步骤(2)所得)的幅值在频率小于15rad/s时，与真实值比较接近，相频则在频率小于5rad/s时与真实值比较接近。而从图7(c)可见，“结果2”的步骤(6)所得相频和步骤(2)所得相频差异较大，这是因为采用非线性最小二乘拟合的优化目标(式(16))是Hf(s)和Hy(s)的幅值和相角共4组数据在采样点处的误差最小。从图7(a)、图7(c)和图7(d)中可见，步骤(6)所得频响和步骤(2)所得几乎完全重合。从辨识“结果2”的数值来看，Tp和Td的估计较准确，而Tn估计误差略大。

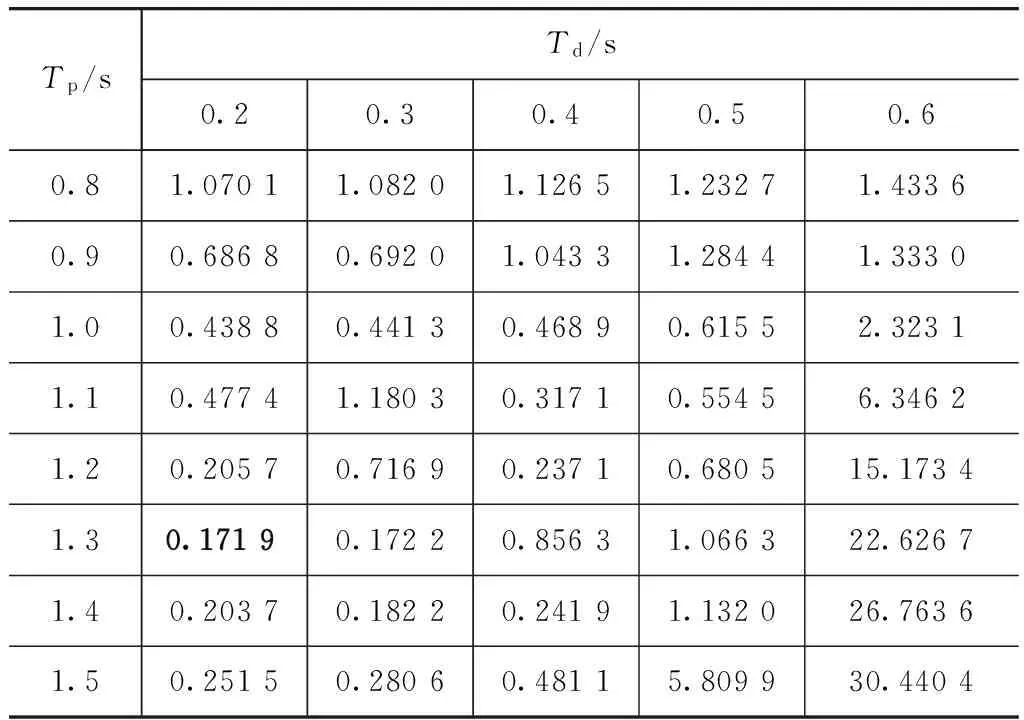
表4 目标函数J计算结果

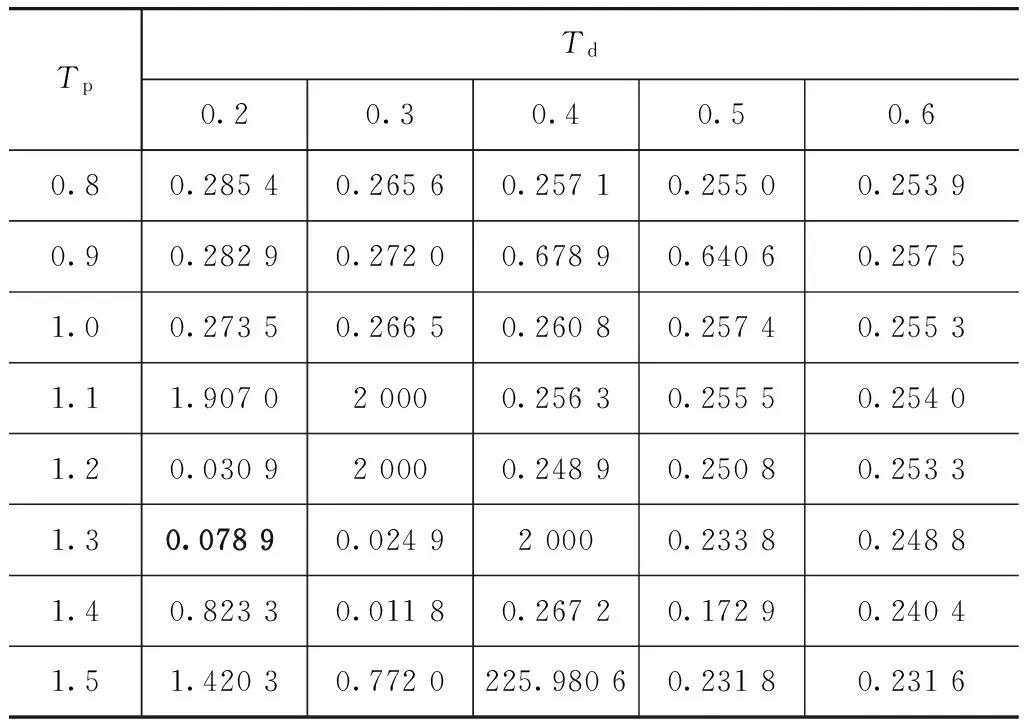
表5 Tn辨识结果 s

为进一步说明辨识方法的稳定性，采用仿真参数不在表3所列点阵的情况下，如取Tp=1.42s，Td=0.2s，Tn=0.1s，再次进行辨识。图8为仿真参数为上述时目标函数J的计算结果，表6为其对应的参数值。从图8可以看出，J值较低的范围也是实际值Tp和Td所在范围。从表6可以看出，J=0.172 1为最小值，相应的辨识结果为Tp=1.4s，Td=0.2s，Tn=0.322s。Tp和Td较接近实际值，而Tn误差较大，这与步骤(2)中传递函数的辨识误差有关，也与在此基础上进行的非线性最小二乘估计引入二次误差有关。

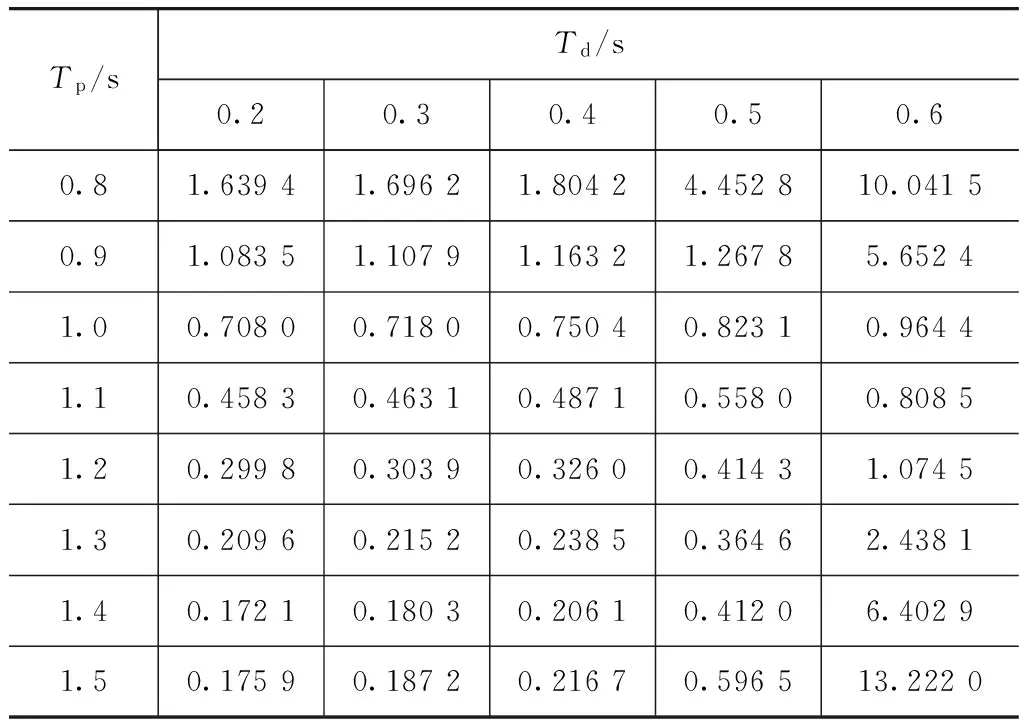
Tp/sTd/s0.20.30.40.50.60.81.63941.69621.80424.452810.04150.91.08351.10791.16321.26785.65241.00.70800.71800.75040.82310.96441.10.45830.46310.48710.55800.80851.20.29980.30390.32600.41431.07451.30.20960.21520.23850.36462.43811.40.17210.18030.20610.41206.40291.50.17590.18720.21670.596513.2220

4 结论

驾驶员模型参数的估计对驾驶员模型在汽车设计和交通安全等领域的应用有重要意义，通过系统辨识的方法估计最优预瞄加速度驾驶员模型的物理参数。采用时域辨识方法，非线性最小二乘法等确定模型参数，并针对仿真数据进行了辨识分析，结果显示该方法对驾驶员模型物理参数的辨识具有良好效果，为驾驶员模型参数的获得提供可行方法。

[1] Plöchl M, Edelmann J. Driver Models in Automobile Dynamics Application[J]. Vehicle System Dynamics,2007,45(7-8):699-741.

[2] Chen Liang-kuang, Lin Hung-ta. On Line Driver Steering Model Estimations[C]. Proceedings of the 8th International Symposium on Automotive Control (AVEC 2006),Taiwan,2006.

[3] Chen Liang-kuang, Hu Dong-young. Adaptive Control with Respect to Driver Model Uncertainty[C]. Proceedings of the 8th International Symposium on Automotive Control (AVEC 2006),Taiwan,2006.

[4] Chen L K, Ulsoy A G. Identification of a Driver Steering Model, and Model Uncertainty, from Driving Simulator Data[J]. Journal of Dynamic Systems, Measurement, and Control,2001,123(4):623-629.

[5] Chen L, Ulsoy A G. Driver Model Uncertainty[C]. American Control Conference, Proceedings of the 1999, IEEE,1999,1:714-718.

[6] Chen L, Ulsoy A G. Identification of a Nonlinear Driver Model via NARMAX Modeling[C]. American Control Conference, Proceedings of the 2000, IEEE,2000,4:2533-2537.

[7] MacAdam C, Bareket Z, Fancher P, et al. Using Neural Networks to Identify Driving Style and Headway Control Behavior of Drivers[J]. Vehicle System Dynamics,1998,29(S1):143-160.

[8] 屈香菊,方振平,王中文,等.测定驾驶员模型的模拟实验研究[J].飞行力学,1992,10(4):62-67.

[9] 屈香菊,方振平.驾驶员结构模型参数辨识[J].航空学报,1996,17(7):63-66.

[10] Odhams A M C, Cole D J. Identification of a Driver’s Preview Steering Control Behaviour Using Data from a Driving Simulator and a Randomly Curved Road Path[C]. Proc. 10th Int. Symp. AVEC.,2010:605-609.

[11] Odhams A M C. Identification of Driver Steering and Speed Control[D]. University of Cambridge,2007.

[12] Guo K, Fancher P S. Preview-follower Method for Modelling Closed-loop Vehicle Directional Control[C]. Proceedings of the Nineteenth Annual Conference on Manual Control, May 23-25,Massachusetts Institute of Technology 1983.

[13] 方崇智,萧德云.过程辨识[M].北京:清华大学出版社,1988.

[14] 管欣.驾驶员方向控制模型及闭环驾驶安全性预测方法的研究[D].长春:吉林工业大学,1992.

[15] 郭孔辉.汽车操纵动力学原理[M].南京:江苏科学技术出版社,2011.

[16] 郭孔辉.预瞄跟随理论与人-车闭环系统大角度操纵运动仿真[J].汽车工程,1992,14(1):1-11.

[17] International Standards Organization (ISO). ISO: 1999-3888 Passenger Cars -- Test Track for a Severe Lane-change Maneuver -- Part 1: Double Lane-change[S]. ISO,1999.

[18] International Organization for Standardization. ISO:2002-3888 Passenger Cars -- Test Track for a Severe Lane-change Maneuver -- Part 2: Obstacle Avoidance[S]. ISO,2002.

[19] 丁海涛,郭孔辉,李飞,等.基于加速度反馈的任意道路和车速跟随控制驾驶员模型[J].机械工程学报,2010(10):116-120.

A Research on Parameter Identification of OptimalPreview Acceleration Driver Model by Tests

Bai Yan1& Jia Xin2

1.SchoolofAutomobile,Chang’anUniversity,Xi’an710064; 2.JilinUniversity,StateKeyLaboratoryofAutomotiveSimulationandControl,Changchun130025

A method to identify the physical parameters of driver model for optimal preview acceleration by tests is presented. Firstly the transfer function of driver model is estimated by time-domain identification and the physical parameters of transfer function are determined by using nonlinear least squares method. Then the preview time and reaction time are optimized by a known objective function. Finally the method is verified by simulation data. The results show that the method presented is very effective for the physical parameter identification of driver model.

driver model; optimal preview acceleration; parameter identification

*教育部长江学者与创新团队支持计划项目(IRT1286)、国家自然科学基金(61473046)和中央高校基本科研业务费专项资金(2013G2222029，2014G3222004，2013G1221017)资助。

原稿收到日期为2014年9月25日，修改稿收到日期为2015年4月20日。