飞行状态受限的多旋翼无人直升机姿态控制
杨成顺, 杨 忠, 葛 乐,
(1.南京工程学院电力工程学院,南京 211167; 2.南京航空航天大学自动化学院,南京 210016)
0 引言
多旋翼无人直升机是指由对称分布在机体四周、正反转成对且个数一般大于等于4 的旋翼提供飞行所需的升力、可机载通信设备、影像采集设备以及各种分析取样设备等有效工作载荷,并能实现垂直起降、自主飞行完成预定任务且可重复使用的不载人航空器,如常见的四旋翼无人直升机[1-3]、八旋翼无人直升机[4]。该类无人直升机因结构简单、超强的机动性、独特的飞行方式以及在军事和民事领域展现出的巨大应用价值,引起了国内外学者以及科研机构的广泛关注,并迅速成为目前国际上研究的热点之一。
然而,国内对多旋翼无人直升机自主飞行控制的研究与国外先进水平之间还有一定的差距,此外,目前所广泛研究的四旋翼无人机的旋翼组件无任何冗余,任一执行机构发生卡死(停转)故障时,都难以实施容错飞行控制,只能任其坠落。因此,多旋翼无人机在构型以及先进飞行控制方法方面都需要进一步深入研究。针对上述问题,提出了一种面对称布局结构的多旋翼无人直升机[5],并针对该无人机的飞行控制问题开展了探索性研究[6-8]。国内外对具有6 个电机配置形式的无人直升机的研究并不多,文献[9]设计出一种3 个轴臂上各2 个电机呈对称结构的六旋翼飞行器,上下对称的电机以相反的方向转动,以抵消产生的反扭矩,并将数学模型在悬停点线性化处理后采用经典PID 算法对其进行了姿态控制研究。
前期研究中已完成该无人机的数学建模,并通过设计合理的干扰估计算法和飞行控制器,使得该无人直升机在受到外界环境干扰以及系统本身存在建模误差和参数不确定等因素影响下具备了优越的飞行性能。然而,该无人机在实际工程应用中不仅受到外部干扰和不确定因素的影响,有时还需对无人机的飞行状态,特别是无人机的姿态角和姿态角速率进行限幅。例如,利用该无人机对输电线路巡检时[10],为了使无人机机载影像采集设备对焦输电线路部件,以采集清晰的线路部件图像,要求无人机的姿态角和角速率的变化范围不能太大;同时还要避免系统反馈控制信号过大引起的执行器饱和问题[11]。
基于上述分析,本文在前期研究的基础上,为了更好地体现和满足该无人机实际工作特点和飞行需求,不仅考虑无人机在飞行过程中会受到不确定以及外界干扰等的影响,同时还在飞行控制系统的设计中进一步综合考虑无人机飞行状态受限情况下的姿态控制问题。
1 数学模型
本文研究的多旋翼无人直升机的外形结构如图1所示。

图1 多旋翼无人直升机外形结构Fig.1 The structure of the multi-rotor unmanned helicopter
为清晰说明该无人机结构中各参数的含义,给出如图2 所示的无人机平面简化结构。图中:l1为旋翼臂OC,OF 的长度;l2为旋翼臂AM,BM,DN,EN 的长度;l3为机身OM,ON 的长度;α 为旋翼臂AM 或BM 与机身对称轴OM 之间所夹锐角。
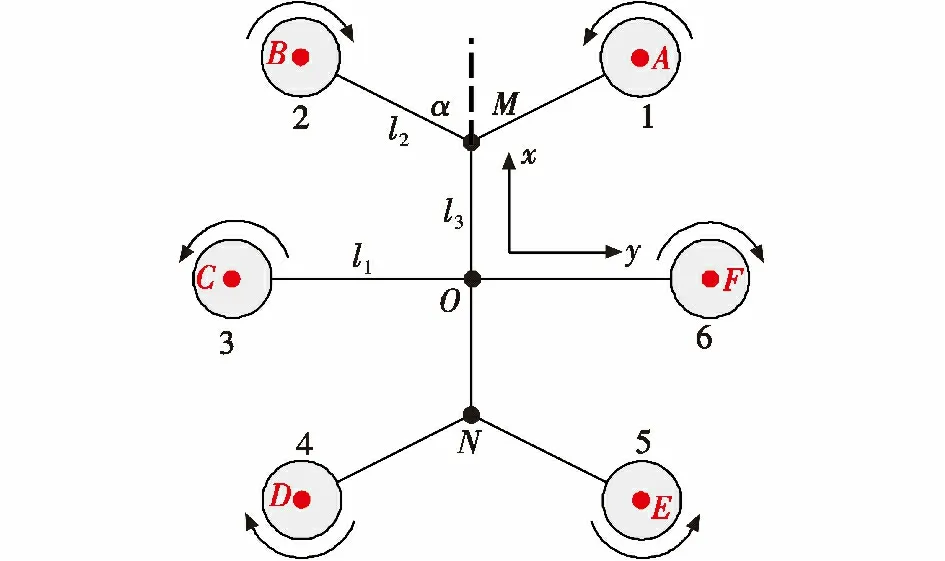
图2 无人机平面简化结构Fig.2 The simplified structure of the unmanned helicopter
为便于对该无人机的建模与分析,首先给出如下合理假设:1)不考虑飞行器负载变化,质心位置始终保持在机体的结构纵轴上;2)飞行器视为刚体,忽略其弹性变形;3)飞行器外形结构和质量分布均匀,质心与坐标系原点重合,且结构完全对称,则其惯性积Ixy=Iyz=Izx。
基于上述假设,并根据Newton-Euler 方程,同时考虑无人机受到的外部干扰以及系统本身的不确定和建模误差的影响,该多旋翼无人直升机的姿态动力学模型,即姿态角方程和角速率方程描述为[8]
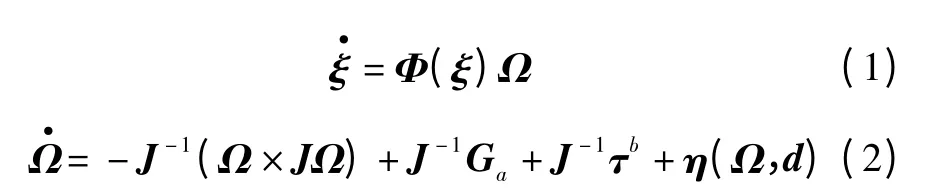
式中:ξ=(φ,θ,ψ)T,为无人机的姿态角向量,φ 为滚转角,θ 为俯仰角,ψ 为偏航角;Ω=(p,q,r)T,为绕机体轴的角速率,p 为滚转角速率,q 为俯仰角速率,r 为偏航角速率;控 制 力 矩],为包括建模误差、内部不确定以及外部干扰在内的姿态系统的复合干扰,并在不引起歧义的情况下,将η(Ω,d)简称为η;J =diag(Jx,Jy,Jz),为无人机的惯性矩阵;Φ(ξ)为角速率到欧拉角速率的转换矩阵;Ga为旋翼陀螺效应力矩。分别表示为
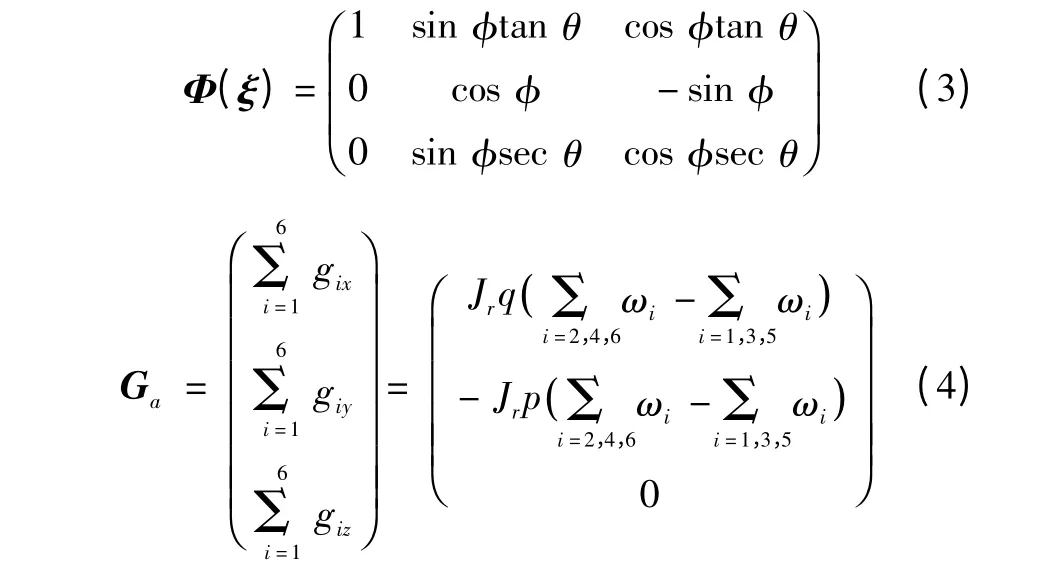
式中:gix,giy,giz(i=1,2,…,6)分别表示第i 个旋翼转动时在机体坐标x,y,z 方向产生的陀螺效应;Jr和ωi分别表示电机的转动惯量和第i 电机的转速。
2 SMDO 复合干扰重构算法设计
干扰观测器技术以其物理意义明确、工程实现方便的优势成为解决不确定非线性系统控制问题的有效方法。它的设计思想是通过构造与原系统并行的新动态系统对原系统中的包括内部不确定、建模误差以及外部扰动在内的复合干扰项进行观测逼近,进而设计补偿控制律以消除复合干扰的影响,并将其与标称系统的控制律相结合来提高系统的鲁棒性。其中,基于滑模控制思想而产生的滑模干扰观测器(Sliding Mode Disturbance Observer,SMDO)以其设计过程简单、易于实现、快速收敛的特点成功应用于飞行控制系统的设计中,如文献[12]采用SMDO 对四旋翼无人机数学模型中存在的干扰进行观测,取得了较好的效果;文献[13]提出基于超扭曲算法的SMDO 以实现对导弹姿态系统中干扰的估计和补偿。
基于此,为实现对多旋翼无人机姿态系统中未知复合干扰的重构,并用于设计补偿控制律,本文设计了如下适用于该无人机的SMDO 复合干扰重构算法。
定理1 针对姿态控制模型角速率方程式(2),构造如下滑模动态
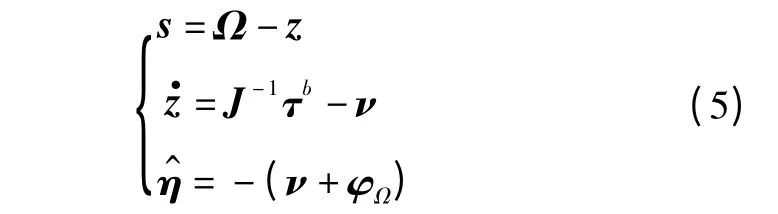
证明 针对式(5)的第一式求导,并将式(2)代入可得
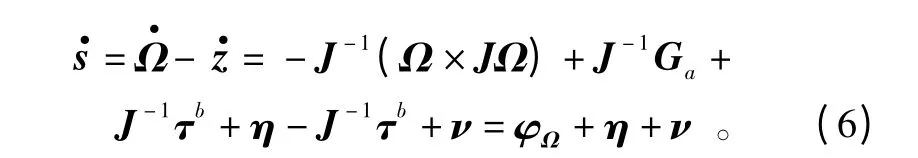
针对式(5),选取如下Lyapunov 函数则当选取

对式(7)求导可得
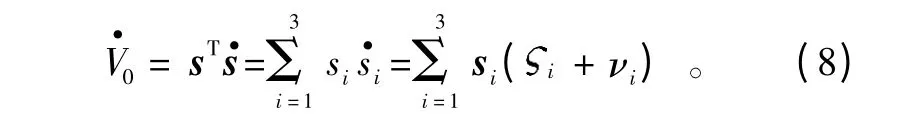
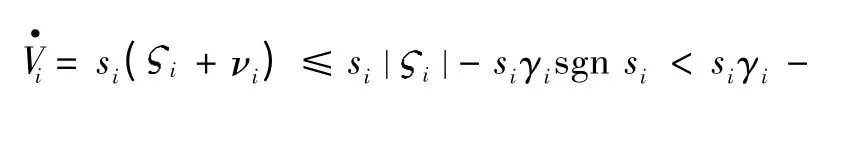

将式(9)代入式(8)可得
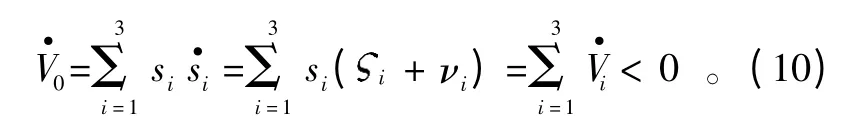
因而,s 在原点平衡状态稳定,且可满足可达性条件。当辅助滑模向量s 及其导数均收敛于原点,即当系统达到稳定的平衡点时,由式(5)可得复合干扰的重构值。证毕。
3 基于SMDO 干扰重构补偿和受限指令滤波的姿态控制器设计及稳定性分析
3.1 控制器设计
首先定义姿态角和角速率的跟踪误差,即

式中:ξc=(φc,θc,ψc)T,为期望姿态角指令;Ωc为期望角速率指令? 经过指令滤波器的输出矢量,Ω*d将在随后定义。
根据式(1)和式(2),姿态角和角速率跟踪误差的导数为
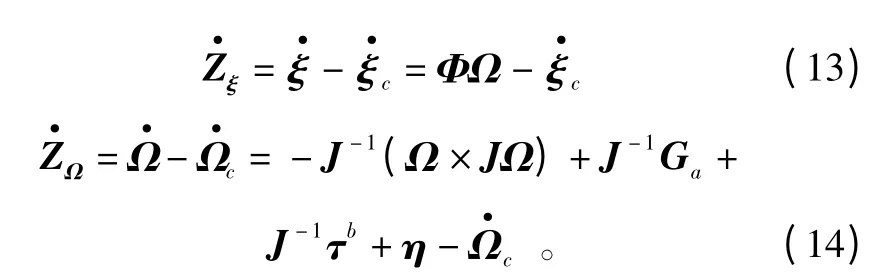
为清晰说明控制器的设计过程,给出如下步骤。
1)针对误差方程式(11)选取如下Lyapunov 函数

对式(15)求关于时间的导数并将式(13)代入,可得
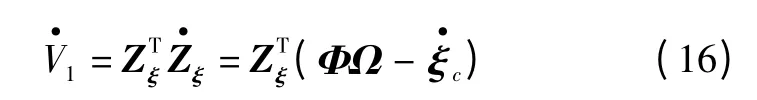
设计如下虚拟控制律
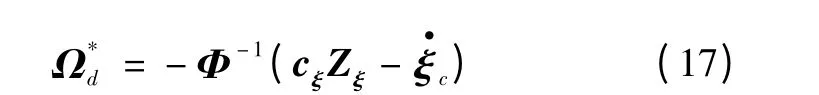
式中:Ω*d为期望角速率指令;cξ为设计的正定参数对角阵。
将式(17)代入式(16)可得

由式(18)可知,所设计的控制律式(17)可使得系统式(13)稳定。
此处,为解决状态受限以及避免回馈递推控制器设计过程中的微分膨胀问题,在姿态控制器的设计过程中引入如图3 所示的指令滤波器。
图3 中:ξ 和ωn分别为滤波器的带宽和自然频率;Ω*d和Ωc分别为滤波器的输入和输出,除此之外,也可通过滤波器获得,因而可避免通过繁琐的解析计算求取Ω*d的微分。

图3 指令滤波器结构图Fig.3 Command filter block diagram
同时,考虑指令滤波器的影响,在严格稳定性分析的基础上引入辅助滤波器ε 来补偿跟踪误差,即
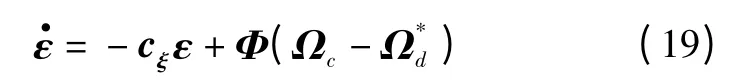
故式(11)所示的姿态跟踪误差可重新被定义为
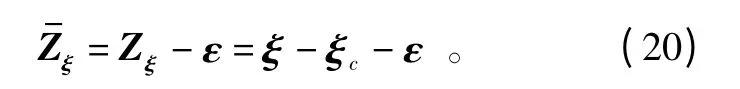
2)设计控制输入力矩τb,以实现飞行器的角速率Ω 渐近跟踪期望角速率Ωc。
针对角速率误差方程式(12),同时兼顾式(20),选取如下Lyapunov 函数
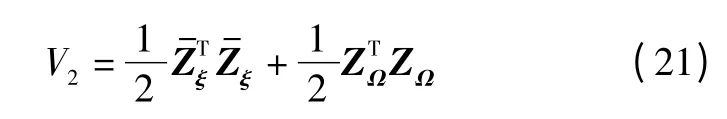
其关于时间的导数为
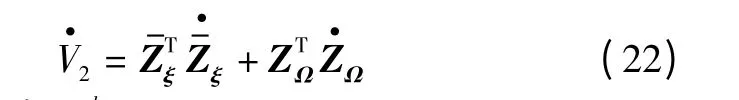
设计如下控制力矩τb,即
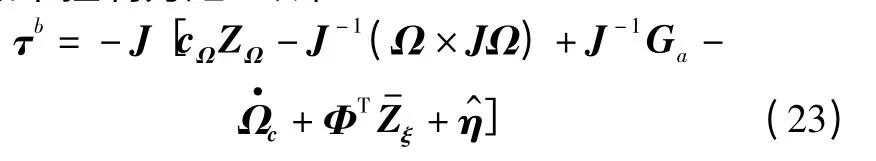
式中:cΩ为待设定的正定对角参数矩阵;η^为由式(5)获得的复合干扰的重构值。
3.2 稳定性分析
基于上述设计过程,给出定理2。
定理2 考虑飞行器的姿态控制系统式(1)和式(2),设计复合干扰重构算法式(5)和选取参数γi那么在虚拟角速率指令式(17)、指令滤波器和辅助滤波器式(19)以及控制力矩式(23)作用下,复合干扰重构值η^ 可一致收敛至真值,且飞行器的姿态角误差Z-ξ以及角速率误差ZΩ均收敛于零,即内回路闭环系统稳定。
证明 根据式(17)、式(19)、式(20)可得
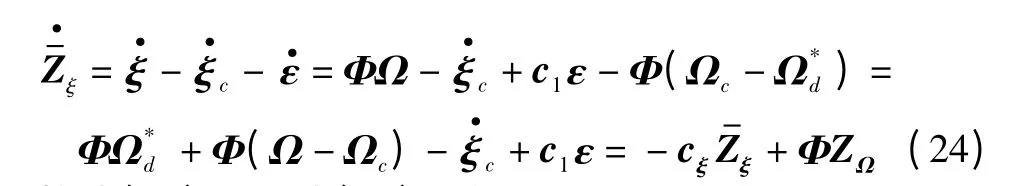
将式(23)代入式(14)可得
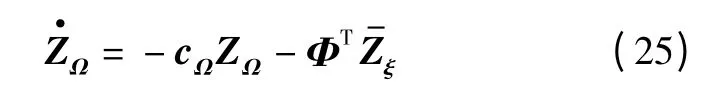
将式(24)和式(25)代入式(22)可得
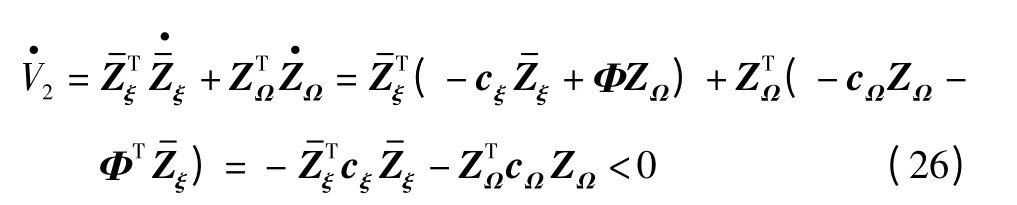
4 仿真结果与分析
为验证所提方法的有效性,利用上述所设计的姿态控制器对该无人机进行姿态跟踪控制。
多旋翼无人机的3 个期望姿态角指令设置为φc=ψc=0.1,初始姿态角和角速率分别为(φ0θ0ψ0)T=(0 0 0)T,(单位为rad),角速率为(p0q0r0)T=(0 0 0)T(单位为rad/s)。在仿真实验中各参数的选择:姿态控制器参数cξ=diag(2,2,2),cΩ=diag(3,3,3);带有幅值和速率受限的指令滤波器参数选择见表1。

表1 指令滤波器参数Table 1 Command filter parameters
多旋翼无人直升机的角速率在回路中受到(0.1cos(0.5t),0.01sin(0.4t)+0.05,0.05cos(0.3t)+0.08)T(单位为N·m)的等效力矩干扰,此实验条件下的姿态跟踪控制响应曲线如图4 所示,其中,dis1 ~dis3 为干扰力矩。
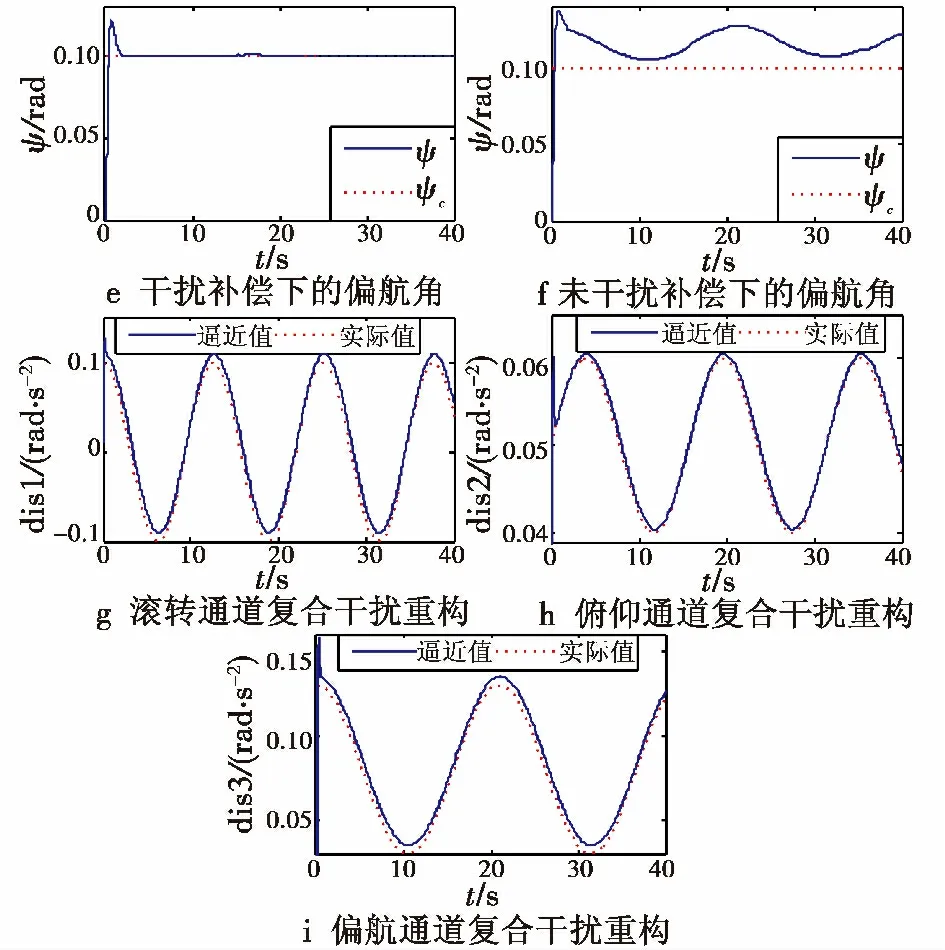
图4 姿态控制响应曲线Fig.4 The response of attitude angles
结果分析如下所述。
1)图4a、图4c、图4e 表示在本文所设计的姿态控制器的控制作用下多旋翼无人直升机的姿态角跟踪响应曲线,从中可以看出,无人机的姿态可以快速、精准地跟踪期望姿态指令,且当期望指令回零时,其姿态也快速保持姿态稳定。图4b、图4d、图4f 表示未对干扰进行补偿下的姿态响应曲线,从仿真结果可以看出,当无人机在飞行过程中受到外部干扰时,如果不对干扰进行补偿,其姿态角的跟踪控制性能将变差,同时角速率也不能趋近于零,即无人机变得不稳定。
2)图4g ~图4i 表示无人机姿态系统中复合干扰的重构曲线。从中可以看出,利用本文所设计SMDO干扰重构算法可以较准确地重构出该无人机姿态系统模型中存在的复合干扰,从而为姿态控制器提供较准确的干扰补偿项。
5 结论
本文在前期研究的基础上,为了更好地体现和满足多旋翼无人直升机的实际工作特点和飞行需求,在考虑无人机飞行过程中不确定以及外界干扰等影响的同时,进一步综合考虑无人机飞行状态受限情况下的姿态控制器的设计问题。仿真结果表明,本文所设计的基于SMDO 复合干扰重构和受限指令滤波的姿态控制器能够使得无人机的飞行姿态快速准确地跟踪给定的指令信号,并能够使得无人机在复合干扰情况下仍具有较好的稳定性和跟踪效果。
[1] GUERRERO-CASTELLANOS J F,MARCHAND N,HABLY A.Bounded attitude control of rigid bodies:real-time experimentation to a quadrotor mini-helicopter[J].Control Engineering Practice,2011,19(8):790-797.
[2] ERGINER B,ALTU E.Design and implementation of a hybrid fuzzy logic controller for a quadrotor VTOL vehicle[J].International Journal of Control,Automation,and Systems,2012,10(1):61-70.
[3] NICOLA C,MACNABA C J B,RAMIREZ-SERRANO A.Robust adaptive control of a quadrotor helicopter[J].Mechatronics,2011,21(6):927-938.
[4] CHEN X J,LI D,BAI Y,et al. Modeling and neuo-fuzzy adaptive attitude control for eight-rotor MAV[J]. International Journal of Control,Automation,and System,2011,9(6):1154-1163.
[5] 杨忠,黄宵宁,李桥梁.新型面对称布局多旋翼飞行器:中国,CN202071985U[P].2011-12-14.(YANG Z,HUANG X N,LI Q L.A novel multi-rotor aircraft with symmetry layout:Chinese Patent,CN202071985U[P].2011-12-14.)
[6] YANG C S,YANG Z,HUANG X N,et al. Modeling and robust trajectory tracking control for a novel six-rotor unmanned aerial vehicle[J].Mathematical Problems in Engineering,2013,673525:1-13.
[7] 杨成顺,杨忠,许德智,等.新型六旋翼飞行器的轨迹跟踪控制[J].系统工程与电子技术,2012,34(10):2098-2105.(YANG C S,YANG Z,XU D Z,et al. Trajectory tracking control for a novel six-rotor aircraft[J]. Systems Engineering and Electronics,2012,34(10):2098-2105.)
[8] 杨成顺,杨忠,葛乐,等.基于RBFNN 和回馈递推的新型多旋翼飞行器控制[J]. 应用科学学报,2014,32(3):301-310.(YANG C S,YANG Z,GE L,et al.Control of a new type multi-rotor aircraft with RBFNN and backstepping[J]. Journal of Applied Sciences,2014,32(3):301-310.)
[9] YIN L L,SHI J S,HUANG Y M.Modeling and control for a six-rotor aerial vehicle[C]//International Conference on Electrical and Control Engineering,2010:1289-1292.
[10] 黄宵宁,郑伟,许家浩,等.输电线路巡检无人机高精度云台设计与实现[J].电子测量技术,2014,37(4):43-47.(HUANG X N,ZHENG W,XU J H,et al.Transmission line inspection precision PTZ design and implementation[J].Electronic Measurement Technology,2014,37(4):43-47.)
[11] 周洪波,裴海龙,贺跃帮,等.状态受限的小型无人直升机轨迹跟踪控制[J]. 控制理论与应用,2012,29(6):778-784.(ZHOU H B,PEI H L,HE Y B,et al.Trajectory tracking control for small unmanned helicopter with state constraints[J]. Control Theory & Applications,2012,29(6):778-784.)
[12] BESNARD L,SHTESSEL Y B,LANDRUM B.Control of a quadrotor vehicle using sliding mode disturbance observer[C]//Proceedings of the American Control Conference,New York City,USA,2007:5230-5235.
[13] 曾宪法,王洁瑶,王小虎,等.基于SMDO 的滑模控制器设计及其在导弹上的应用[J].航空学报,2011,35(5):873-880.(ZENG X F,WANG J Y,WANG X H,et al.Design of sliding mode controller based on SMDO and its application to missiles control[J]. Acta Aeronautica et Astronautica Sinica,2011,35(5):873-880.)

