基于非均匀海水固有光学性质的透明度计算方法
陈 希, 于 斌, , 何君姮, 孔凡龙, 李宗叶
(1.解放军理工大学 气象海洋学院, 江苏 南京 211101; 2.91206部队训练部, 山东 青岛 266108; 3.东海舰队37分队, 浙江 宁波 315122; 4.71901部队, 山东 聊城 252000)
海水透明度是指透明度盘铅直沉入海水中的最大可见深度, 是军事海洋环境的关键要素, 对探潜、反潜及潜艇隐蔽等活动具有重要的军事意义。目前,获取海水透明度包括, 海水透明度盘测量、经验公式计算、激光雷达探测、卫星资料反演等多种方法。
利用透明度盘测量海水透明度是海洋调查工程中广泛使用的一种常规方法, 但是受海况、人为差异等外界因素的影响较大, 观测数据具有一定的主观性和随意性, 存在较大误差; 海水透明度计算的另一种方法是基于经验公式, 如张绪琴等[1]基于海水均匀的假设, 提出了海水透明度与光束衰减系数和漫射衰减系数之和成反比的经验公式, 适用于均匀海水透明度计算; 在激光测量透明度方面, 姜璐等[2]分析了机载激光雷达最大探测深度与海水透明度之间的比例关系, 该方法适用于水深 30 m以浅海域;在卫星遥感反演透明度方面, 何贤强等[3]使用SeaWiFS卫星遥感资料, 建立半经验模式反演海水透明度, 该方法适用于一类水体。
上述研究中, 透明度盘方法存在主观性、随意性缺点; 利用表观和固有光学性质数据计算透明度的方法一般是基于海水光学均匀性假设开展的相关研究。本文基于垂直非均匀海水分层思想, 引入蒙特卡罗方法, 提出并建立了一种基于海水固有光学性质的海水透明度计算模型。
1 海水透明度计算模型
利用透明度盘测量海水透明度原理示意图如图1。当入射光穿透海水照射到透明度盘上, 透明度盘反射太阳光, 产生透明度盘上涌光, 盘具有一定的亮度。同时海水由于对光有后向散射等作用, 产生海水上涌光, 海水具有一个背景亮度。于是在透明度盘处,透明度盘和海水存在亮度差异, 即固有对比度。透明度盘上涌光和海水上涌光传递到人眼处, 两者仍然存在亮度差异, 即为相对对比度, 若此时人眼能感知到相对对比度, 则透明度盘可见。不断下放透明度盘的深度, 当人眼感知不到相对对比度时, 认为透明度盘已经下放到透明度深度, 则可测得海水透明度。本文在仿真晴空条件下透明度盘测量原理基础上, 建立非均匀海水透明度计算模型的基本思路如下: 假设透明度盘位于深度D处, 其上涌光相对量为uD, 通过uD计算透明度盘的固有对比度, 代入非均匀水体对比度传输方程求解到达人眼处的相对对比度, 与人眼阈值进行比较, 若相对对比度大于人眼阈值, 则D达到了海水透明度所在深度,得到海水透明度值, 反之, 增大D, 进行新一轮计算, 计算流程如图2所示。其中, 海水上涌光相对量、透明度盘固有对比度及相对对比度的计算方法是该模型的关键, 下文将对这3个问题进行详细论述。

图1 透明度盘测量海水透明度原理图Fig.1 Schematic of transparency disc measuring water transparency

图2 基于固有光学量计算海水透明度算法流程图Fig.2 Calculating water transparency based on inherent optical quantization
1.1 海水上涌光相对量的计算方法
假设透明度盘在D处的上涌光相对量为uD, 向上辐照度为Eu, 向下辐照度为Ed, 则有:

Eu和Ed分别描述了水下光场上涌光和下涌光能量的分布情况, 而水下光场的能量分布, 可以利用蒙特卡罗方法, 跟踪光子运动过程, 达到稳定状态时,对光子能量进行统计和累加得到,Eu和Ed的计算步骤如下(图3)。
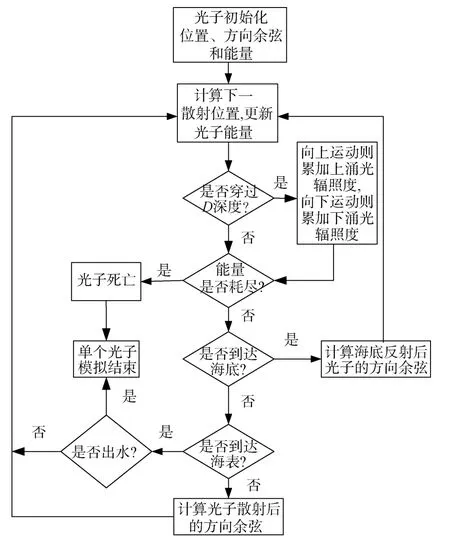
图3 蒙特卡罗方法跟踪光子水下运动过程流程图Fig.3 Flow diagram of tracking photon underwater movement based on Monte Carlo method
第一步: 初始化光子能量、入射方向和位置;
第二步: 计算光子下一个散射点的位置及能量;
第三步: 根据散射前后位置关系, 若光子自下而上穿过深度D的海水薄层, 则将光子能量累加到向上辐照度, 若向下穿过, 则累加到向下辐照度, 若不能穿越, 光子继续运动;
第四步: 根据能量阈值判断光子能量是否耗尽,若耗尽则认定光子死亡, 转向第一步, 进行新一轮模拟;
第五步: 若光子并未死亡, 则判断光子是否到达海表或海底, 若到达海表则判断是否发生全反射,若发生全反射, 计算反射后光子的能量、坐标和运动方向余弦, 若出水, 则进行新一轮模拟; 若到达海底,则计算反射或者散射后的方向和能量; 若未到达海表和海底, 则计算光子散射后的方向余弦, 转向第二步。
在上涌光相对量计算过程中, 涉及光子散射点位置、运动方向余弦和能量的计算, 光子运动到海底、海面时运动方向余弦和能量的计算, 在透明度盘深度处的海水上涌光和下涌光辐照度的统计计算,相关计算方案如下。
1.1.1 光子散射位置、运动方向和能量的计算
1.1.1.1 光子散射位置
以水平的海表面为x-y轴, 垂直水平面向下为z轴建立直角坐标系, 如图4所示。假设光子在p= (x,y,z)处发生散射后, 其方向向量为μ={μx,μy,μz}, 能量为E, 下一次散射点的坐标p′ = (x′,y′,z′), 方向向量为能量为E′, 由于光子运动的几何路径远小于水深, 可认为光子在两次散射之间所经历的几何路径为直线, 则下一个散射点的坐标为

图4 光子水下运动参数几何关系示意图Fig.4 Schematic of relation among geometric parameters of photon underwater movement

式中l表示光子走过的几何路径, 在均匀水体中,l可由光学衰减长度s和衰减系数c确定[6]:
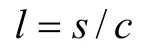
在非均匀水体中, 可将水体分为若干层, 每一层中的水体光学性质近似均匀, 假设每一层光子经过的光学衰减长度为si, 衰减系数为ci, 则光子穿过的几何路径长度为:

根据蒙特卡罗方法的基本原理[7], 光学衰减长度s= -lnq, 式中q为区间[0,1]上服从均匀分布的随机数。
1.1.1.2 光子散射后运动方向
由图3中的散射后各参量的几何关系, 通过余弦定理可计算光子散射后运动方向向量μ′:
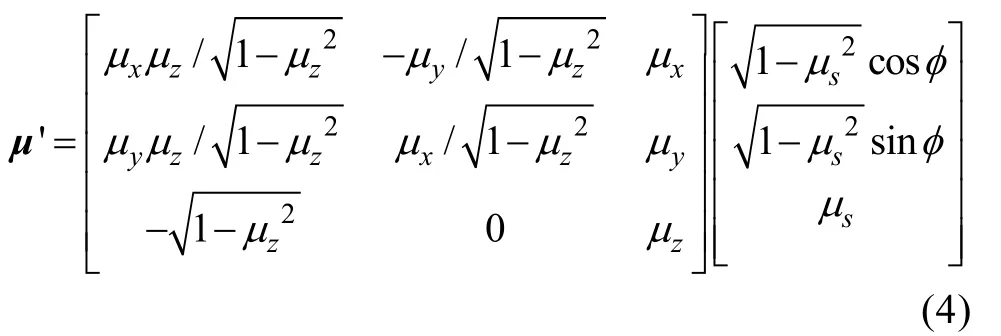
式中,φ为水平散射角, 满足φ=2πq,q为区间[0,1]上服从均匀分布的随机数。sμ表示散射角sθ余弦, 根据Robert 等[9]的研究有

其中q为区间[0,1]上服从均匀分布的随机数,g是不对称因子。
1.1.1.3 光子散射后能量
光子散射后的能量:

式中,sp分别为光子散射位置水体的散射系数。
1.1.2 海底对光子运动方向和能量的影响
假设光子碰撞海底前的坐标为p= (x,y,z), 方向余弦为μ={μx,μy,μz}, 能量为E, 碰撞后的坐标为p′ = (x′,y′,z′), 方向余弦为μ′= {μx′,μy′,μz′}, 能量为E′, 海底深度为H, 海底对光的反射可以看作是郎伯反射面, 则根据朗伯反射面的性质, 可以得到如下关系[10]:
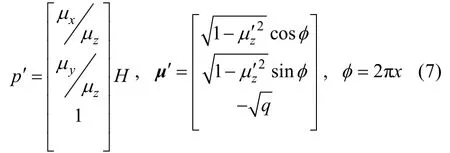
其中,q和x分别为区间[0,1]上服从均匀分布的随机数。若海底反射率为bρ, 则光子撞击海底后, 其能量变化为

由方程组(7)可以计算光子碰撞海底后的坐标以及运动的方向余弦, 根据(8)式, 可以更新光子的能量。
1.1.3 海面对光子运动方向和能量的影响
光子运动到海面后的方向和能量会受到波浪起伏的影响, 波浪起伏可以看作是若干小的倾斜平面组成的, 根据斯涅尔定律, 利用倾斜平面的斜率和入射方向可计算光束在海表处反射或折射的运动方向。由于出水后蒙特卡罗方法对单个光子模拟过程结束, 故在此只讨论发生全反射时光子反射方向和能量变化情况。
设光子在坐标p=(x0,y0,z0)处发生全反射,p所在平面的方程可由倾斜平面的仰角和方位角进行计算, 全反射前光子的运动轨迹直线方程可由全反射点、运动方向余弦唯一确定, 则可以确定直线上z坐标高于p的任意一点X, 根据直线与平面位置关系可以计算X关于倾斜平面的对称点X′, 向量up=X-p的单位向量即为反射方向向量, 计算得到:
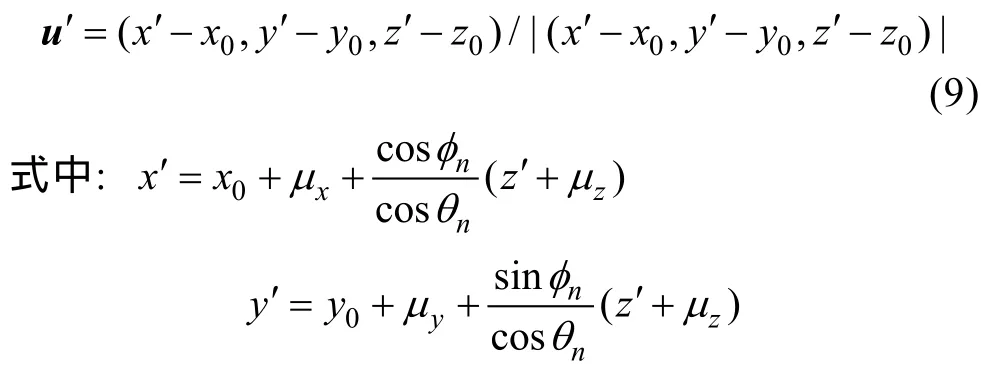
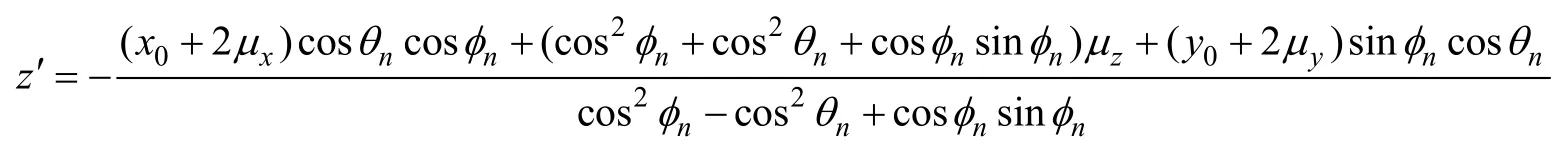
θn、φn分别为波浪面的仰角和方位角。φn可认为是[0,2π]上均匀分布,θn的概率分布函数[8]为:
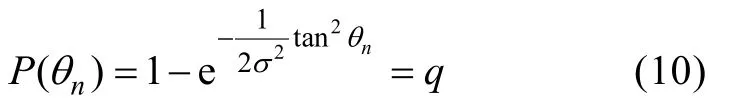
其中,σ2= 0.003 + 0.00512v,v为海表风速。根据概率分布函数的归一性, 可以计算θn:

(11)式确定了倾斜平面的法线方向。
光束从海水中射向空气中时, 若光线相对于波浪面法线的入射角iθ满足光的全反射条件:

则在波浪面上, 光线发生全反射, 此时, 光子的运动方向与原方向关于波浪面法线对称, 能量等于原能量与海表反射率的乘积。
反之, 若
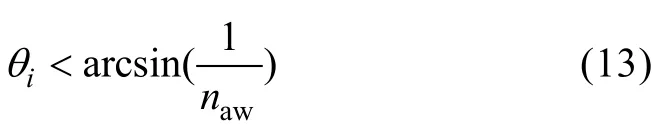
则光子穿透水面折射入大气, 光子运动符合折射定律, 通过折射定律可以计算光子的出射方向, 其能量等于原能量与海水折射率的乘积, 即则光子能量的变化为:

其中E为穿越前能量, 穿越后为E′,naw为海水相对于空气的折射率, 一般情况下, 空气的折射率为 1,而海水相对空气的折射率可取为naw=1.34。
1.1.4 上涌光辐照度和下涌光辐照度的计算
深度D处的上涌光辐照度Eu和下涌光辐照度Ed即可通过对光子能量统计和累加的方式计算出来。若光子向上穿越深度D处的均匀薄水层, 即μz<0, 则将光子在垂直方向上的能量累加到上涌光辐照度中, 即

若光子向下穿越深度D处的均匀薄水层, 即μz>0,则将光子在垂直方向上的能量累加到下涌光辐照度中, 即

根据(1)式, 即可计算深度D处的上涌光相对量。
1.2 固有对比度和相对对比度的计算
使用上涌光相对量计算透明度盘在深度D处的固有对比度CD[1]:

式中Dρ为透明度盘漫反射率。
在垂直方向上, 因为人眼距离水面较近, 故人眼到水面之间的衰减可以忽略不计, 将固有对比度作为输入, 通过对比度传输方程式(16), 即可计算透明度盘到达眼睛的相对对比度C为[9]:

式中li为透明度盘向上直到水面距离上各光学均匀层的厚度,Ki为漫射系数, 可在蒙特卡罗方法模拟光子水下运动时根据其定义进行计算[14]。
2 数值实验
利用上述建立的透明度计算模型, 进行透明度计算实验, 采用 Australian Antarctic Division的BROKE-WEST_ACS数据集中 2006年 1、2月份59.8°~68.1°S、30°~80°E 海区的实测固有光学性质垂直剖面数据、海表面风速和透明度盘观测数据进行验证, 具体步骤为:
第一步: 设置透明度盘的初始深度d为 0.1 m,固有光学性质数据的垂直分辨率为2 m, 实验海区水深取100 m(据海水透明度观测数据统计表明, 一般不超过70 m), 海水分层为50层。
第二步: 运用蒙特卡罗方法模拟水下光场, 其光子总数设为 1 000万个, 根据 Duntely等[4]和Gilbert[5]的研究, 设光子的初始能量值为 1个单位,光子死亡能量阈值取为0.000 1, 初始位置随机设定,初始方向为太阳天顶角。对模拟过程中穿过了d的薄水层的光子, 采用式(1)、式(13)、式(14)对计算d上的上涌光相对量uD, 并通过漫射衰减系数的定义,计算d上的漫射衰减系数k;
第三步: 将uD代入式(15), 计算透明度盘在d上的固有对比度Cd, 并通过式(16)计算到达人眼的相对对比度Cri;
第四步: 比较相对对比度Cri与人眼对比度阈值0.002, 若Cri> 0.002, 则将d增加0.1 m并转向步骤1), 否则, 认为d为海水透明度D并输出结果。计算流程如图5所示。
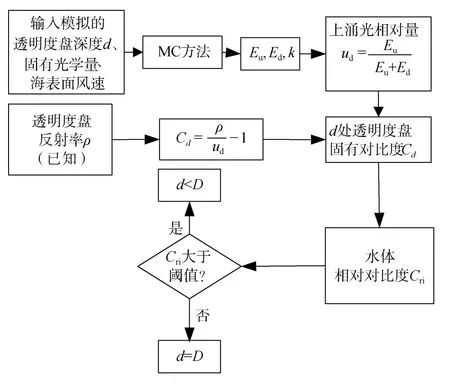
图5 数值计算流程图Fig.5 Circuit of numerical methods
将模型计算的海水透明度值与37个站点的透明度盘实测数据进行了对比, 如图6所示, 计算值与实测值接近, 平均绝对误差为1.1 m, 平均相对误差为9%, 取得了较好的效果, 说明本文的模型是可行的。
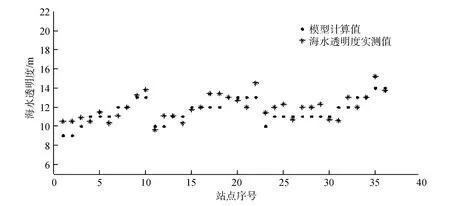
图6 计算透明度盘模型计算结果与实测值对比图Fig.6 Comparison of transparency disk model calculation results and measurements
3 总结和讨论
1) 本文建立了基于非均匀海水固有光学性质,仿真晴空条件下透明度盘测量海水透明度的基本过程, 将蒙特卡罗方法与对比度传输方程相结合, 计算海水透明度的数学模型。
2) 该模型克服了透明度盘测量方式易受天气、海况和人工影响等缺点, 计算模型仅为依赖于海水固有光学性质, 对不同海区具有通用性, 为夜间探测海水透明度增加了一种新途径。
3) 数值实验结果与海水透明度观测数据比较表明, 平均绝对误差1.1 m, 证明该方法可以客观、定量、准确的计算海水透明度。
4) 受到海水固有光学性质实测数据的限制, 数值实验验证样本相对较少, 下一步研究中, 将利用不同海区、不同季节的海水透明盘观测数据对模型计算精度进行进一步验证和改进。
[1] 张绪琴.海水透明度[J].海洋湖沼通报, 1982, 4:14-17.
[2] 姜璐, 朱海, 李松, 等.机载激光雷达最大探测深度同海水透明度的关系[J].激光与红外, 2005, 35(6):397-399.
[3] 何贤强.利用 SeaWiFS反演海水透明度的模式研究[J].海洋学报, 2004, 26(5): 55-63.
[4] Mobley C D.Light and Water [M].New York: Academic Press, 1994.
[5] Capone A, Digaetano T, Grimaldi A, et al.Measurements of light transmission in deep sea with the AC9 trasmissometer[J].Nuclear Instruments & Methods in Physics Research A, 2002, 487(3): 423-434.
[6] Robert A.Leathers, Monte Carlo Radiative Transfer Simulations for Ocean Optics[M].Washington: NRL,2004: 9.
[7] Lerner R M, Summers J D.Monte Carlo description of time and space resolved multiple forward scatter in natural water [J].Applied Optics, 1982, 21(5):861-869.
[8] Xu Z.A DNS capability for obtaining underwater light field and retrieving upper ocean conditions via in-water light measurements [D].Massachusetts: Massachusetts Institute of Technology Department of Mechanical Engineering, 2011.
[9] Jerlov N G.Marine Optics [M].Amsterdam: Elsevier Scientific Public, 1976.
[10] 陈文革, 黄铁侠.机载海洋激光雷达的试验研究[J].电子学报, 1998, 26(9): 21-24.

