把准三个点，提高数学课堂实效

江苏常州武进区芙蓉小学（213118） 杨 洁

在数学课堂中，经常会发现教师上得满头大汗、耗时费力，学生的作业仍错得一塌糊涂，究其原因，是教师没有把握好教学要点。要想使数学教学更具实效，笔者认为，教师要从把准新知生长点、把准新知生成点及把准学生困惑点三个方面入手进行教学。

一、把准新知生长点

在数学教学中，教师只有准确把握学生的认知起点，因势利导讲解新知，才能使教学更具实效。

案例：“小数加减法”教学片断

师：小刚买一支钢笔用了6．75元，小丽买一个文具盒用了3．5元，你知道小刚和小丽一共花了多少钱吗？谁能通过列算式来解决这个问题？

生1：6．75＋3．5。

师：这个算式正确，请大家运用自己学过的笔算方法来算一下。

生2（列式如右）：我是按照元、角、分的定义来算的，即元和元相加、角和角相加、分和分相加。

生3（列式如右）：我是按照整数加减法的法则来计算的，即先把数字对齐，再把各部分相加减。

师：你们觉得哪种算法正确？同时说明理由。

生4：第一个同学的算法正确，因为各个数字的单位是一样的；第二个同学在计算时知道对齐数位，但是忽视了各个数位上数字表示的意义是不同的，只有相同单位的数字才能够进行加减计算。

师：说得非常好。由此可见，整数加减法的法则在小数加减法里同样适用，不同的是，在计算小数加法时要由整数加减法中的末尾对齐改为小数点对齐，从低位算起。

从上述教学可以看出，教师恰当地从学生的已有知识经验入手，让学生先自行解决问题，再进行必要的点拨、引导。这样既讲清了新知的要点，又提高了教学效率。

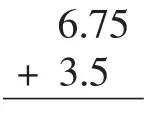
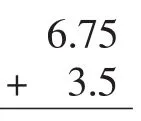
二、把准新知生成点

在新课程理念指导下，教师要把课堂真正还给学生，让学生勤于动脑、乐于思考，并及时捕捉学生思维的亮点、新知的生成点，通过恰当的点拨、引导，使学生获得新的数学思想和方法。

案例：“等式和方程的意义”教学片断

师：请大家仔细看图，并根据自己的理解把天平两端物体之间的关系表达出来。

生1：x＋50＞100，x＋50＝100，x＋50＜100，x＋x＝100。

师：如果老师让你把这些式子分类，你能做到吗？

生2：x＋50＞100，x＋50＜100 为一类；x＋50＝100，x＋x＝100为一类。

师：能把你的理由说一说吗？

生2：前两个式子是不等的关系，后两个式子是相等的关系。

师：很好！这后两个式子就是我们今天所要学习的重点，我们把含有未知数的等式叫做方程。请大家仔细观察这句话，哪些词比较关键？

生3：“含有未知数”和“等式”比较关键。

师：很好！那么，你知道方程和等式之间的区别吗？

生4：方程一定是等式，但等式不一定是方程。

从上述教学可以看出，在比较中得出方程与等式的区别是本课新知的生成点，对于基础好、悟性高的学生来说这部分知识比较简单，但对于大多数学生来说，由于初次接触方程，教师还是应该在新知的生成点上讲明、讲清，从而使学生对所学的新知印象深刻。

三、把准学生困惑点

在数学教学中，教师不能自己认为重要的就多讲，自己认为不重要的就少讲或不讲，而应准确把握学生的困惑点，真正起到教师传道、授业、解惑的教育职责。

案例：“因数和倍数”教学片断

师：谁能说说，24的因数有哪些？

生1：4、6。

师：除了这两个数以外还有吗？大家再仔细找找。

生2：1、3、8……

师：要想一个不漏地将因数找出来，最好采用哪种办法？

生3：从小到大地写。

师：非常好！那么一个数的倍数在寻找的时候又具有哪些特点呢？下面，就请大家以2的倍数为例说一说。

生4：2、4、6、8……

师：从一个数的倍数中，你发现了什么？

生5：一个数的倍数是无限的。

师：那么，怎样才能准确把握因数和倍数的特点呢？（多媒体出示表格说明）

上述教学中，教师抓住学生学习的困惑点，通过细化、比较的方式，强化学生对因数和倍数特征的认识，使学生学得轻松明了，很快就突破了教学难点。

总之，在数学教学中，教师只有立足学生已有的知识经验，才能使学生在数学上得到不同的发展。