一种分块的基础矩阵鲁棒计算方法

李 兵，邱儒琼,2

（1.湖北省基础地理信息中心，湖北 武汉 430074；2.中国地质大学（武汉），湖北 武汉430073）

一种分块的基础矩阵鲁棒计算方法

李 兵1，邱儒琼1,2

（1.湖北省基础地理信息中心，湖北 武汉 430074；2.中国地质大学（武汉），湖北 武汉430073）

针对基础矩阵计算过程存在异常数据的问题，提出了一种新的匹配点分块的基础矩阵鲁棒计算方法。该方法首先对特征点集进行分块处理，然后以点到基线的距离为最优化准则获得较为准确的特征点匹配集，最后以8点算法获得结果值。实验表明，设计的算法切实可行，对特征点错误匹配所造成的误差影响有较大的压制效果。

计算机视觉；极线几何；基础矩阵；鲁棒估计法

从二维影像中获取所拍摄场景的三维信息是摄影测量与计算机视觉等学科研究的热点内容之一[1]。对于某个场景的单幅影像，通常无法简单地从中获得所拍摄场景三维信息。为了获得场景中的三维信息，传统的方法是采用2个相机组成的立体视觉系统，或者使用单个相机从不同角度拍摄同一场景2次以上，才有可能达到目的。在无其他场景先验知识或者相机运行信息的情况下，2幅影像是通过极线几何关系来关联的，它的代数表示就是基础矩阵[2]。基础矩阵以一种简洁的方式将同一场景的2幅影像关联起来，它的精确计算问题是计算机视觉领域中的一个重要问题，也在其他的学科领域中广泛应用[3-6]。

目前，针对基础矩阵常用的计算方法可以分为线性方法、迭代方法和鲁棒方法[7]。其中，线性方法计算速度最快，但由于它在计算过程中忽略参数间的约束关系并且其最小化准则缺乏物理意义，因此估计精度较差。迭代方法所获得的计算精度较高，但计算时间相对较长，且不能消除特征点错误匹配所造成的影响。为此，许多学者引入统计学中的鲁棒回归分析理论，提出了一些估计基础矩阵的鲁棒方法，如RANSAC方法[8]、M-estimators方法和最小平方中值（LMeds）方法[9]等。

由于鲁棒方法能够有效地抑制异常数据的影响，因此得到了更加广泛的应用。针对原始匹配点对基础矩阵的不同影响，本文改进了经典算法，提出了一种新的鲁棒算法，其基本思想就是利用分块的策略进行抽样，然后以点到极线的距离最小为最优化准则得到误差相对较小的内点集，最后以分块基础矩阵的鲁棒扩充算法获得最终结果。

1 数学模型

1.1 基于分块的随机抽样策略

如图1所示。首先量测出所有待匹配点的平面坐标，并获得坐标值中的最大值和最小值，然后由最大值与最小值把第一幅图像中的匹配点划分成b×b块。各个块中若有匹配点则保留，若没有则剔除掉。为了获得8个点的子样本，在第一幅影像上随机抽取互不相同的8个数据块。其后在每块中随机抽出1个匹配点，从8个数据块中共得到8对分布比较均匀的匹配点，用这样的8对匹配点计算基础矩阵相对来说较为稳定。

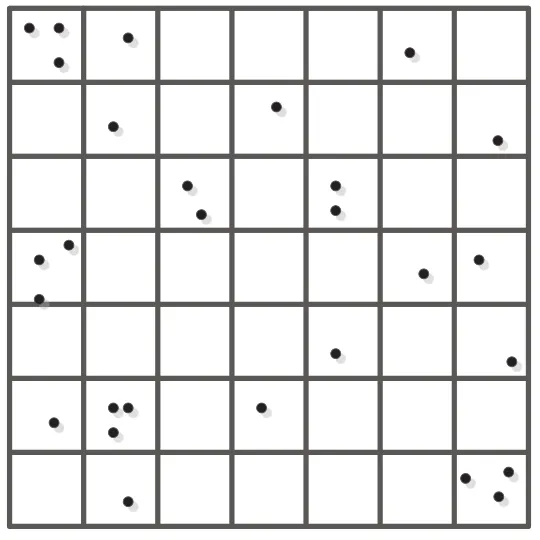
图1 数据分块示意图

在理想情况下，错误匹配在空间中均匀分布，每块中有相同数目的匹配点且随机抽取是均匀分布的。但实际情况中却并非如此。某一块中的匹配点数目和另一块中的匹配点数目可能并不一致。所以，一个在含有较少匹配点的块里，匹配点被抽取的概率要比在含有很多匹配点的块里大得多。为了让所有的匹配点被抽取的概率尽量相同，本文采取一种新的策略来保证随机采样的均匀性，具体方法如下：

假设一共有l个特征点块，将数值区间[0,1]分成l个间隔，并设定第i个间隔的宽度等于其中ni为第i个块中的匹配点个数。在数据块的随机抽取中，如果产生的一个0～1的随机数落在第i个间隔上，那么第i个块就认为被选中了。由此，可以保证匹配点随机抽样的均匀性，用该策略代替普通的随机采样去获得特征点子集，计算得到基础矩阵的结果会比较稳定和准确，如图2。

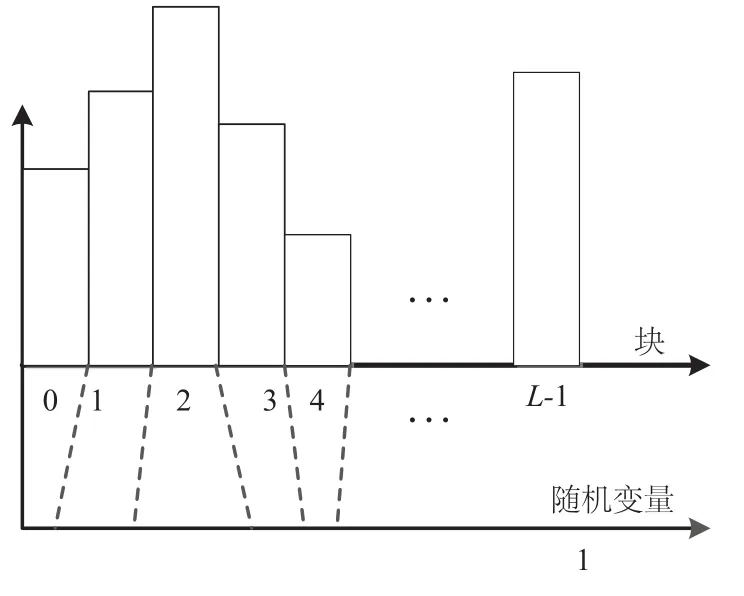
图2 分块抽取原理

1.2 错误匹配点剔除

要进行基础矩阵的估计，首先要剔除误差较大的匹配点。基于改进的最小平方中值算法获得内点集的思路如下：

首先，利用上一节介绍的特征点分块随机抽样策略进行多次随机采样以获得多个子样本，并采用改进的8点线性算法估计基础矩阵的近似值，并作为后续迭代运算的初始值。

然后，计算所有匹配点的对极距离，并把对极距离（计算方法如式（1）所示）作为匹配点的误差值。由于误差受很多因素的影响，可以假定它是服从高斯分布的，即99.87%的误差分布在3σ（σ是均方差）以内，把误差大于3 σ的匹配点作为异常匹配点，并把它们剔除掉，得到一组新的匹配点。

最后，用这组新的匹配点计算基础矩阵新的近似值，并一直循环下去，直到相邻2个基本矩阵的近似值偏差小于一定的阈值或循环已经达到一定的次数。那么，去除异常数据点后得到的点集就认为是内点集。

1.3 基于分块基础矩阵的鲁棒扩充算法

对原始匹配点进行异常点剔除操作后，可以获得一个误差相对比较小的内点集。但是，用该内点集中的匹配点去求解基础矩阵所得到的结果，很有可能并不是最优解，其原因主要有以下2点：

1）内点集中每个特征点的误差并不完全相同，用误差较小的部分特征点去求解基础矩阵，所获得结果的精度肯定要高于用内点集中所有匹配点计算获得的结果。

2）最小二乘法的最优化准则是通过极小化由特征点坐标构成的系数方程而进行迭代计算的。但是，这种极小化的原理没有具体的物理意义，其计算获得的解不能代表真正的最优解。

所以，如果能够在内点集中获得误差比较小的部分子集，那么该子集可以称之为最优子集。同时，由该子集按照具有实际物理意义的最优化准则进行计算所获得结果就可以解决上述两个问题，认为是最优解。

1.4 算法流程

具体的算法步骤可以分为以下5步，如图3所示。

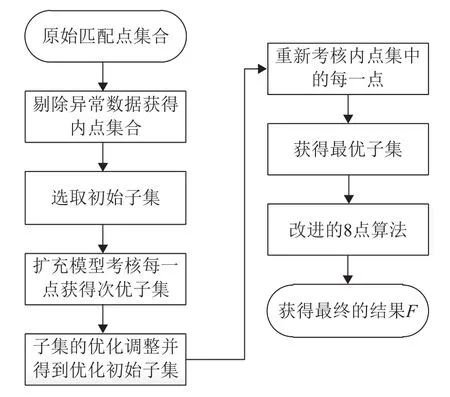
图3 算法流程图

1）获得特征点的内点集合。

2）获得基础矩阵的当前近似值所对应的8个匹配点为初始子集,用其中的元素计算基础矩阵以及点到极线的距离平方总和。

3）下述过程重复N-8次（N是特征点的个数，减去8是因为开始已经选取了8个特征点）。①从集合S中取出一对不存在的匹配点，加入其中形成新的子集，并计算和；②若是则接受该匹配点，否则剔除该匹配点。

4）对子集进行优化调整。

5）使用该最优子集并采用8点算法计算出基础矩阵的最终值。

2 实验与结论

如图4所示，使用走廊立体像对影像作为实验数据来验证本文的算法。图中画出了由本文算法得到的部分极线，表1以平均余差和平均对极距离指标为评价依据，分别列出了改进的8点算法、LMedS算法以及本文算法的计算结果。考虑到误差的随机性，对图4的影像进行了多次实验，每次选取不同数目的匹配点，以多次计算结果的平均值作为最终结果进行比较。

从表1可以看出，改进的8点算法由于难以应对错误匹配点的影响，所以计算获得的误差较大，由此得出的基础矩阵结果值不可靠。LMedS算法去掉了绝大部分的错误匹配点，计算得到的精度明显比改进的8点算法好。但是，由于LMedS算法在去掉部分匹配点后，剩余的匹配点所采用的计算策略相同，没有区分它们的误差大小而统一地进行计算，所以得到的结果并不是最优的。而本文算法依据其误差大小运用扩充模型在内点集中选取最优子集后再进行计算，所以获得的基础矩阵结果精度最高，偏差最小。

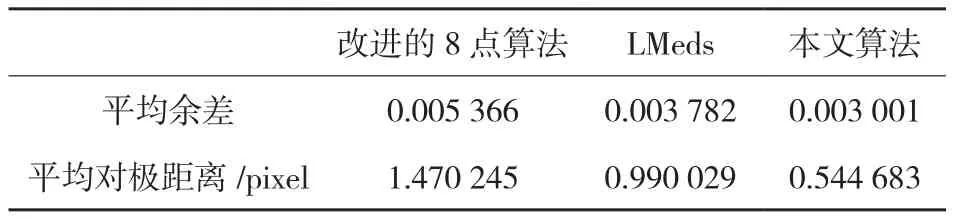
表1 3种不同算法的结果

图4 走廊的立体像对

[1] Hartley R, Zisserman A, Ebrary I. Multiple View Geometry in Computer Vision [M]. Cambridge Univ Press, 2003

[2] Armangu X, SalvI J. Overall View Regarding Fundamental Matrix Estimation [J]. Image and Vision Computing, 2003, 21(2): 205-214

[3] 徐巧玉, 叶东, 车仁生. 基于光学参考棒的立体视觉测量系统现场标定技术[J]. 光学学报, 2008, 28(1): 81-86

[4] 徐巧玉,车仁生. 基于光学测棒的立体视觉坐标测量系统的研究[J]. 光学学报, 2008, 28(11): 2 181-2 186

[5] 张旭苹, 汪家其, 张益昕， 等. 大尺度三维几何尺寸立体视觉测量系统实现[J]. 光学学报, 2012, 32(3):148-155

[6] 丁雅斌, 彭翔, 田劲东， 等. 一种三维数字成像系统的多视点姿态估计方法[J]. 光学学报, 2007, 27(3): 451-456

[7] Zhang Z. Determining the Epipolar Geometry and Its Uncertainty: A Review[J]. International Journal of Computer Vision, 1998, 27(2): 161-195

[8] Fischler M A, Bolles R C. Random Sample Consensus: a Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[J]. Communications of the ACM, 1981, 24(6): 381-395

[9] Torr P H S, Murray D W. The Development and Comparison of Robust Methods for Estimating the Fundamental Matrix[J]. International Journal of Computer Vision, 1997, 24(3): 271-300

P231.5

B

1672-4623（2015）01-0012-02

10.3969/j.issn.1672-4623.2015.01.004

李兵，正高职高级工程师，现主要从事地理信息系统等科研和应用方面的工作。

2014-05-26。

项目来源：数字制图与国土信息应用工程国家测绘地理信息局重点实验室开放研究基金资助项目（GCWD201204）。