Boost变换器混杂系统建模与仿真

李自成，李志远，刘新芝，王后能

武汉工程大学电气信息学院，湖北 武汉 430205

Boost变换器混杂系统建模与仿真

李自成，李志远，刘新芝，王后能

武汉工程大学电气信息学院，湖北 武汉 430205

为了得到Boost变换器在负载和输入电压扰动下稳定的输出电压，针对Boost变换器的混杂动态系统特性提出了一种新的控制算法．首先根据混合动态系统理论建立变换器的混杂自动机模型，从而将控制算法的设计问题转换为混杂自动机切换条件的选取．然后通过对电感电流连续模式及电感电流断续模式工作过程的分析，采用电路理论法计算得到切换条件．最后采用MATLAB的Simulink和Stateflow工具箱对控制算法进行了仿真．结果表明设计的控制算法可以实现Boost变换器全范围的稳定运行，同时对负载和输入电压扰动都有很好的抑制效果．

Boost变换器；混杂动态系统；混杂自动机；电流连续模式

0 引言

由于电感电流存在连续模式（Continuous Current Mode，以下简称：CCM）与断续模式（Discontinuous Current Mode，以下简称：DCM）两种模式，使得对Boost变换器的仿真建模变得复杂．近年来，随着混杂动态系统理论研究的深入，越来越多的学者尝试将混杂动态系统理论应用于DCDC开关变换器的建模和控制［1］．目前，在电力电子领域中，应用最为广泛的是切换线性系统模型以及混杂自动机模型．文献［2］根据李雅普诺夫稳定性，作为判定系统是否稳定的条件，从而提出了一种类滑模的新型控制方式，虽然这种控制方式对于电感电流连续模式有很好的效果，却并没有对电感电流断续模式进行讨论，使得结果变得不完整；文献［3］基于系统的切换线性模型，研究了电感电流连续模式下，系统的分析了整个模式下的能观性、能控性、能达性等基本理论，但是也没有对基于该模型下的切换系统进行综合；文献［4］指出了混杂自动机模型可以构成电力电子电路模型，同时给出一种数值计算方法，用于确定系统的最大稳定半径，并给出了一种以给定的两种性能不同的切换率以使系统稳定的系统设计的方法．

笔者首先对负载及输入电压扰动时Boost变换器的能量传输过程进行了分析，然后利用电感电流峰值与输出电流的比较，得到CCM与DCM每个模式之间的切换条件，从而建立Boost变换器的混杂自动机模型．最后，通过Matlab／Stateflow实验平台对理论分析进行建模仿真验证．仿真结果表明采用混杂系统控制策略对Boost变换器输出电压稳定性方面具有良好的控制效果．

1 Boost变换器的混杂动态系统建模

混合自动机模型H一般由6个元素组成的集合来表示［5］：

其中，F:Q→（X→Rn）是在每个离散状态下定义的利普希茨连续矢量场；I:Q→2X为每一个q∈Q，指定的一个X不变集合；E⊆Q×Q是一系列可达的离散转换集合；G:E→2X定义每一个e＝（q，q）∈E边界［6－7］．

混合系统相对于动态系统理论来说是符号的变化情况，系统状态在动态连续时间系统中，表示的是所述轨迹或差分方程的解的一个点，而在混杂动态系统的状态下是将系统保持，同时满足特定条件的情况［8－9］．

图1给出了Boost变换器的混杂自动机模型及每个状态与Boost电路的状态之间的关系．图片上方是离散状态机，下方则为连续状态机，这两部分共同构成了混杂自动机模型．通过连续信号x（t）的变化使得离散状态机之间实现了转换，同时连续信号则依赖于离散符号σ={σ1，σ2，σ3}进行转换，为了控制Boost变换器的输出电压，需要确定所有离散状态的边界条件．从图1可知，Boost变换器有q1（SW1 on，SW2 off），q2（SW2 on，SW1 off），q3（SW1 off，SW2 off）3种离散状态工作方式［8］．设Gij表示模型由模式i向模式j的切换条件．所以，只要确定两个边界条件即可控制电感电流连续模式；对于电感电流断续模式，则需要确定G12、G23、G31三个边界条件．这里采用电路理论法来确定切换条件．

图1 Boost变换器的混杂自动机模型Fig.1 Hybrid－automation representation of the boost converter

2 Boost变换器的切换条件

对于混杂动态系统而言，控制设计的问题本质上就是切换条件的选择问题，而CCM与DCM每个模式都有自己特有的切换条件［10］．

2.1 电感电流连续模式

图2所示为Boost变换器在电感电流连续模式下的电感电流和输出电压波形．图2中Ip、IL分别为电感电流iL的峰值、平均值，ΔiL为IL中的纹波；Vo为输出电压vo的平均值，ΔVo为Vo中的纹波，dT为系统在mode1与mode2之间切换的时刻，T是变换器转换回mode1的时刻，同时也是开关频率f的倒数．

图2 CCM模式下状态变量的近似变化Fig.2 Approximate variation of state variables in CCM

由图2可知，在0≤t≤dT时，

同时，电容上的电压变化为：

从而得到输出电压纹波和电感电流纹波的关系：

在CCM模式下，当确定了输出电压需要稳定的波动范围后，只需要确定G12和G21边界条件即可．两个模式之间切换的控制条件可以通过电感电流与其平均值之间的变化关系来定义．这里通过变换器输入输出功率之间的关系得到：

综上所述，可以确定切换条件

2.2 电感电流断续模式

图3为Boost变换器DCM模式下电感电流和输出电压波形．其中d1T为系统处于mode1的时间间隔，同理，d2T和d3T分别为系统处于mode2、mode3的时间间隔．由图可知，mode3时iL为0，电路为DCM状态，且d3T=（1－d1-d2）T．

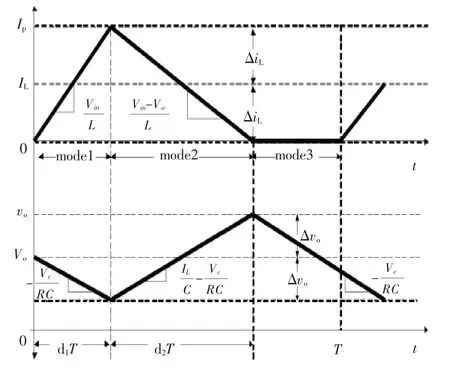
图3 DCM模式下状态变量的近似变化Fig.3 Approximate variation of state variables in CCM

从图3可知：在0≤t≤dT时，电感电流直线上升，输出电压直线下降．当t＝dT时，电感电流达到峰值，为：

根据平均电感电流与电感电流峰值之间的关系得到：

另外，从图3可得：

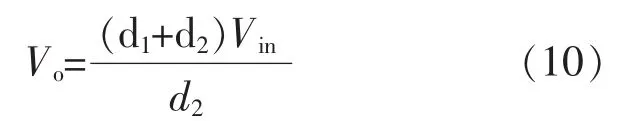
输出平均电流为：

根据输出平均电流与平均电感电流之间的关系，有：

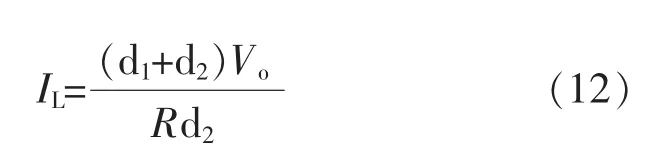
所以：

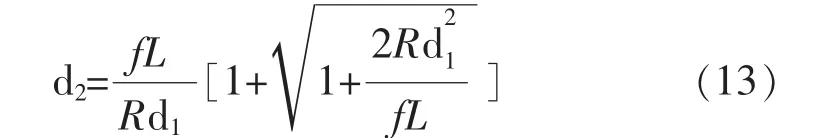
由于负载平均电流与流过二极管的平均电流相等，所以在DCM，有

整理有：

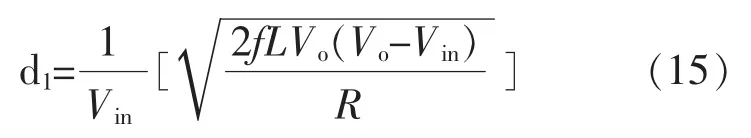
根据以上分析，可以推导出与频率相关的电感电流的峰值为：

综上，切换条件G12由Ip确定，切换条件G23可以选择电感电流iL＝0，为了确保在电压下降时电压波动vo相等，可以选择vo＝Vo作为切换条件G31．所以有：

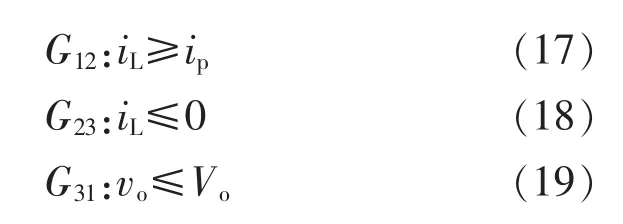
切换条件G12中的电感电流峰值Ip与开关频率有关，所以确定开关频率的范围就尤为重要．开关频率可以根据输入电压范围不超过电压纹波±Δvo来确定，则：

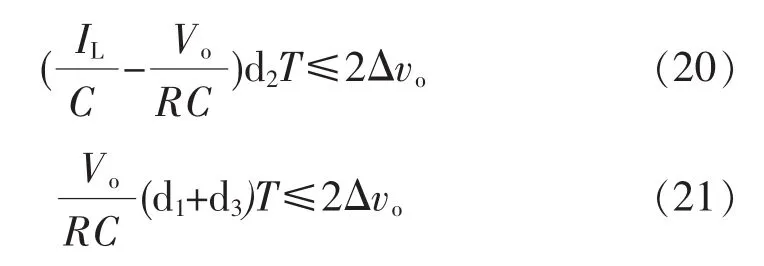
通过上面的不等式有：

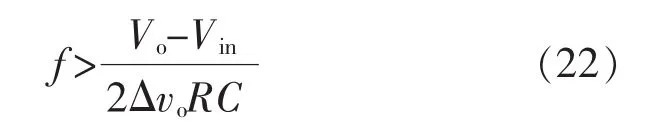
这样选择的开关频率，就可以通过保证输出电压在所要求的范围内．通过对更高的开关频率进行仿真，结果显示：开关频率越高，输出电压中的纹波电压越小，但更高的开关频率会带来输出电压Vo中心值下降．所以，开关频率应该在上式的基础上慎重选择，根据实际需要选择合适的开关频率．

3 仿真研究

在Matlab／simulink环境下，利用其自带的stateflow模块，设计了Boost变换器混杂系统仿真模型．仿真模型如图4所示．模型参数如下：给定输入电压36 V，理想输出电压为60 V，电感L＝6．72× 10－4H，电容C＝6．6×10－4F，电压波动Δvo＝0．5 V．根据已经确定好的边界条件来设定Boost变换器离散状态在stateflow中的边界条件．

图5为负载突变时的仿真结果．当t＝0时，输入电压为36 V，负载R＝20 Ω，系统运行于CCM模式，输出电压迅速升压到达预期电压60 V；当t＝0．03时，系统的电阻R由20 Ω增加到40 Ω，系统工作于CCM与DCM的边界，但仍处于CCM状态；当t＝0．06时，电阻R由40 Ω增加到80 Ω，系统工作于DCM状态．

图6为系统在输入电压变换情况下的仿真波形．当t＝0．062时，输入电压由36 V突然增加到40 V，由图6可以看出，在输入电压变化的条件下，电感电流出现一定的波动，而输出电压基本没有受到影响．通过以上几组仿真结果，可以看出无论是负载扰动还是输入电压扰动，本文所设计的混杂控制算法在保持输出稳定电压性能上都具有很好的效果．

图4 Boost变换器在simulink中的仿真图Fig.4 Boost converter simulation map in simulink

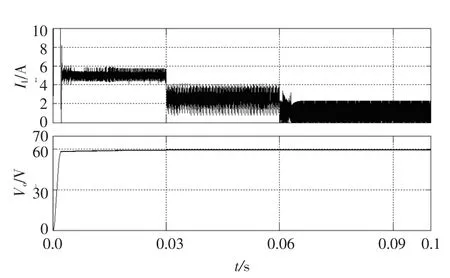
图5 电感电流与输出电压的波形图Fig.5 Inductor current and output voltage waveforms

图6 输入电压、电感电流与输出电压的波形图Fig.6 Input voltage,inductor current and output voltage waveforms

4 结语

笔者设计了一种基于混杂动态系统理论的Boost变换器的控制算法，控制问题被简化为根据混杂自动机模型确定切换条件的问题．最后通过simulink和stateflow工具箱，在MATLAB平台对提出的控制算法进行了仿真验证．结果表明在负载扰动和输入电压扰动下，采用笔者设计控制算法的Boost变换器，可以保持良好的输出电压稳定性．该方案的主要特点有以下5个方面：

a．设计的算法计算量非常小，使其成为一个不错的实时控制的选择．

b．设计的算法包括Boost变换器的完整的工作范围（CCM模式和DCM模式）．

c．笔者设计的控制算法可以应用于其他的变换器．

d．该方案具有在CCM模式下，可变的开关频率，拥有最大范围的输出电压．同时，在DCM的运作也非常流畅．无论是在CCM和DCM的操作，保护条件取决于负载值，准确的负载电流传感器是必需的．

e．笔者设计的控制算法并没有考虑寄生元件产生的影响，这样方便计算．

致谢

湖北省科学技术厅和武汉工程大学提供了资金支持，在此表示感谢！

［1］莫以为，萧德云．混合动态系统及其应用综述［J］．控制理论与应用，2002，19（1）：1－8．

MO Yi-wei，XIAO De-yun．Overview of hybrid dynamic system and its application［J］．Control Theory and Applications，2002，19（1）：1－8．（in Chinese）

［2］马皓，祁峰，张霓．基于混杂系统的DC－DC变换器建模与控制［J］．中国电机工程学报，2007，27（36）：92－96．

MA Hao，QI Feng，ZHANG Ni．Modeling and control for DC－DC converters based on hybrid systems［J］．Proceeding of the CSEE，2007，27（36）：92－96．（in Chinese）

［3］薛林，姚国兴．基于双向DC－DC变换器的光伏发电系统［J］．电气传动，2010，40（11）：29－32．

XUE Lin，YAO Guo-xing．Bidirectional DC－DC converter based photovoltaic power system［J］．Electric Drive，2010，40（11）：29－32．（in Chinese）

［4］SENSKY M，EIREA G，KOO T．Hybrid modeling and control of power electronics［J］．Proceeding of 6th International Workshop on Hybrid Systems：Computation andControl，LectureNotesinComputerScience．Springer，2003，26（23）：450－465．

［5］杜贵平，张波，张涌萍，等．基于切换线性系统的DCDC变换器矩阵系数多项式描述模［J］．中国电机工程学报，2006，26（21）：65－70．

DU Gui-ping，ZHANG Bo，ZHANG Yong-ping，et al．Matrix coefficient polynomial description model of DCDC converters based on switched linear systems［J］．Proceedings of the CSEE，2006，26（21）：65－70．（in Chinese）

［6］GUPTA P，PATRA A．Hybrid mode－switched control of DC－DC boost converter circuits［J］．IEEE Transactions on Circuit and Systems－II：Express Briefs，2005，52（11）：734－739．

［7］SREEKUMAR C，AGARWAL V．Hybrid control algorithm for voltage regulation in DC－DC Boost converter［J］．IEEE Transaction on Industrial Electonics，2008，55（6）：2530－2538．

［8］魏克新，高国振，李华平，等．用于电池测试系统的双向DC／DC变换器的研究［J］．电气传动，2010，40（2）：37－40．

WEI Ke-xin，GAO Guo-zhen，LI Hua-ping，et al．Research of bi－directional DC／DC converter using in the battery test system［J］．Electric Drive，2010，40（2）：37－40．（in Chinese）

［9］袁雷，沈建清，肖飞．电流控制模式Buck－Boost变换器建模及非线性现象仿真［J］．中南大学学报：自然科学版，2012，43（2）：972－976．

YUAN Lei，SHEN Jian-qing，XIAO Fei．Modeling and nonlinear phenomena simulation of current－mode controlled Buck－Boost converter［J］．Journal of Central South University：Science and Technology，2012，43（2）：972－976．（in Chinese）

［10］王振．基于平均法的DC－DC变换器建模综述［J］．广西电力，2011，34（5）：48－50．

WANGZhen．SummarizationofDC／DCconverter based on average method［J］．Guangxi Electric Power，2011，34（5）：48－50．（in Chinese）

Hybrid modeling and simulation of boost converter

LI Zi－cheng，LI Zhi－yuan，LIU Xin－zhi，WANG Hou－neng
School of Electrical and Information Engineering，Wuhan Institute of Technology，Wuhan 430205，China

To get a stable output voltage of boost converter under load and input voltage disturbances，a new control algorithm based on the hybrid features of boost converter was designed．Firstly，an exact hybrid automation model was built based on hybrid dynamic systems theory，and the problem of control algorithm design was equivalent to the guard－selection problem of hybrid automation．Then，the current flowing process was analyzed both in the continuous inductor current mode and in the discontinuous inductor current mode．The guard conditions were based on a circuit theoretical approach．Finally，the hybrid control algorithm was implemented by using simulink platform and the state flow chart feature of Matlab．The simulation results indicate that the boost converter can run under full operating ranges and has inhibitory effects on both load and input voltage disturbances by the proposed hybrid control algorithm．

boost converter；hybrid dynamic system；hybrid automations；continuous current mode

TP17

A

10.3969/j.issn.1674-2869.2015.02.012

1674-2869（2015）02-0054-05

本文编辑：苗变

2014－12－25

湖北省自然科学基金项目（2014CFB776）；武汉工程大学科学研究基金（K201420）

李自成（1977－），男，湖北广水人，博士，副教授．研究方向：混杂系统的建模与控制、电力电子与传动、计算机集成控制.