探析高中数学作业设计模式

李侠

《普通高中数学课程标准》要求，高中学生做作业的目的在于巩固和消化所学教材的基本知识，把基础知识转化为基本技能，并发展基本能力。但是现在高中学生的课余时间较少，作业多，学习压力普遍感觉大，而自愿完成作业的学生较少，大多数是迫于高考的压力或教师、父母的督促。作为教师，我们该怎样面对这种现象呢？几年来，笔者一直反思和探索，并进行了相关的实践研究。

一、传统作业存在的问题和分析

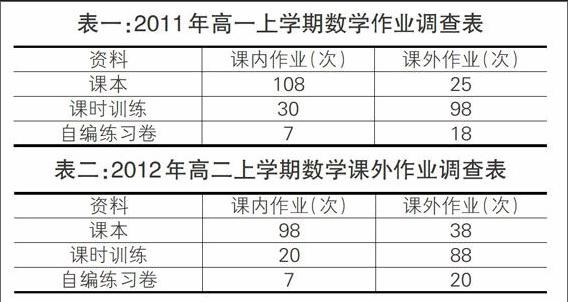
从上表高一和高二的作业布置可以看出，数学作业大多是直接从课本、课时训练上选择的，而书上的习题主要是巩固性练习。自编的练习卷实际上也是从网上或其他资料中搜集到的一批习题中剪拼而成的。这种作业有许多弊端，如：作业都是老师统一布置，形式单一;对作业的评价基本上是教师来讲解出错的题目。从而使大多数学生的学习成了上课听讲后完成作业的一种被动学习。

从表三可以看出高三的数学作业基本上以数学辅导书和试卷为主，形式是以做题和讲题为主。

从上表可以看出高一和高二大多数学生对作业能完成。对待数学的态度大部分不是太喜欢，但抄袭或不做作业的比例少，而高三的学生不同，一部分学生能完成作业，感到厌烦抄作业或不做的现象比例比高一和高二要大。这说明目前的高中数学作业已形成了许多较具操作性的模式，在培养学生做题能力方面起到很明显作用，但这种作业在培养学生的创造性思维和创新能力还有待于提高。

另外，在调查中发现有些学生反映数学的作业较多，作业多导致学生课业负担增重，学生学习的积极性减弱，这不是减少作业能解决的问题，这需要考虑课外作业对学生学习内容的有效性。数学课外作业的有效性能直接决定着教学目标是否实现，是实施课程标准的需要。数学课外作业的有效性也能直接决定着数学课堂的正常运转。因此，怎样布置数学课外作业才能有效在课堂教学中显得非常重要。

二、作业模式的探索

作业模式改革的目的是促进学生全面发展，调动学生的积极性、主动性和创造性，巩固和拓展所学知识。教师必须有针对性地对教学目标实施落实到位，按照课堂教学内容的要求布置作业，作业要精选，以便更好地巩固课堂教学内容。

（一）分层作业

高中的学生因认知水平、思维能力、和初中学习基础等方面的不同导致他们理解和接受新知识的能力也不同。在整个高中阶段，教师如果采取全班学生都做同样作业，就会出现各种各样的问题。有的学生觉得很简单，有的学生就得有点难度，也有的学生根本看也看不懂。这样时间长了，就会使一部分学生逐渐失去学习数学的兴趣，甚至有的学生会放弃数学的学习。因此，在平常教学中，教师应根据教学内容的要求和不同层次的学生的学习能力，设计层次不同的作业。

作业示例：《不等式教学》

（1）求函数[y=x+4x（x>0）]的最小值。（学困生）

（2）若[x>54]，求[f（x）=4x+14x-5]的最小值。（中等生）

（3）若[x>-1]，求[f（x）=（x+5）（x+2）x+1]的最小值，并求相应[x]的值。（优等生）

这三道题的练习就基本不等式的学习对三种类型的学生分别要求会做、理解和提高三个层次的要求。这样设计作业类型让不同层次的学生都有体会成功做题的机会，从而提高他们学习的积极性。教师在一个教学单元结束时会进行单元性检测，让不同层次的学生发现各自的问题。教师可以根据检测的结果将学生分成不同的类别，如合格和需努力两个不同的层次;优秀、良好和不及格三个层次。教师会根据学生的错误题目再找些题目让学生进行分层次练习，使他们进一步巩固和提高。

（二）自主作业

教师按照教学单元提供数学的巩固性作业，是根据学生的能力所选取适当难度的作业题，这部分一般是与教学内容相关的延伸题和拓展题，让学生根据自己的学习能力自由选择完成。

作业示例：《同角三角函数关系》

（1）已知[tanα=12]，[α∈（π，2π）]，则[cosα]的值是_______。

（2）若[cosα=-35]且[tanα>0]，则[tanα·cos3α1-sinα]的值是_____________。

（3）已知[tanα=3]，求[sinα-cosα]的值。

（4）已知[sinα=12]，又[α]是第二象限角，求[cosα]，[tanα]的值。

（5）已知[tanα=3]，求[sinα]和[cosα]的值。

（6）若[sinθ=m-3m+5]，[cosθ=4-2mm+5]，其中[θ]为第二象限的角，则[tanθ]=_______。

（7）已知[θ]为第二象限角，且[sinθ+cosθ=15]，那么[tanθ]=_______。

（8）已知;[tanx=-43]，求值：（1）[sinα+cosαsinα-cosα];（2）[5sin2α+3cos2α]。

这样做，尊重了学生的选择，改善了作业效果，为学生的更好发展提供了自由学习的机会，也让学生享受到了作为作业主人的快乐。

（三）自编练习或测验作业

课后教师可以指导学生自编练习作题，学生之间相互做，相互测评。开始时，学生可能不习惯，这就需要教师指导学生怎么编题，如可以把做过的题目变一变数字形成新题目，也可以考虑题目条件和结论是否能调换一下等等。每次编题后要求学生交给教师审核，检查情况。

自编检测练习示例：《集合》（苏教版必修一）

（1）若[x2∈{1，0，x}]，则实数[x]的值为______。（课本教材第10页第5题改编）

（2）已知集合[A={x|ax2-3x+2=0}]至多有一个元素，则[a]的取值范围是______。（课本教材第19页第1题改编）

（3）已知集合[{0，1，2}?A?{0，1，2}]，，则[A]的子集个数是______。（课本教材第19页第10题改编）

（4）集合[M={x|x=k+14， k∈Z}]，[N={x|x=k2-14， k∈Z}]，则它们之间的关系是______（同步练习册改编）

（5）已知方程[x2-px+15=0]与[x2-5x+q=0]的解集分别为[A]与[B]，若[A∩B={3}]，则[p+q]的值是______。（课本教材第14页第12题改编）

（6）已知全集[U=R]，集合[A={x|x<-3或x>3}]，[B={x|x<1或x>5}]，求[A∩B]，[A∪B]，[A∩（CUB）]。（课本教材第14页第11题改编）

（7）已知集合[A={x|x≤2， x∈R}]，[B={x|x≥a}]，且[A?B]，则实数[a]的取值范围是_____________。（课本教材第10页第7题改编）

（8）设集合[A={x|a≤x≤a+3}，][ B={x|x<-1， 或][x>5}]，若[A∩B≠?]，求实数[a]的范围。（同步练习册改编）

（9）已知集合[A={x|x2-3x+2=0}]，[B={x|x2-ax+][1=0}]，若[A∪B=A]求实数[a]的取值范围。（课本教材第18页第15题改编）

这种做法发挥了以往考试评价未曾发挥的交流作用，学生在自己编题的过程中学会了对知识的归类和整理，在一定程度上深化了对知识的运用，同时增强了学生的自信心，还有助于教师的教学。这种做法，为学生的被动学习变主动学习提供了有利的条件。每个班的高中学生的学习结果不可能一样，教师通过单元性测验可以看看学生的学习情况。而且教师在一个教学单元结束时测验，这样做有利于学生在教学单元的学过程中能自主选择作业，还能帮助提高学生完成作业的主动性和积极性。

（四）研究性作业

在完成新课教学后，笔者经常在给定范围后由学生自己选题，指导他们去调查数据和搜集整理资料、学生相互交流和评价。等作业完成后要以研究报告、小论文等形式上交给教师。如：函数模型结束后让学生利用放假时间到农村、工厂、商店等做调查，了解函数模型在生活中的应用，收集一些生活中的函数模型实例（指数函数、对数函数、分段函数等），并做出分析，写出调查报告。这种做的研究成果与同学交流，增强了学生学习的数学的兴趣和信念，同时培养了学生的合作意识和创新精神。

作业是高中数学教学过程中的一个重要环节，通过它能反馈教学，既能检查学生的学习效果，也能检验教师的教学效果。正确组织好高中数学作业的设计，对于培养高中学生的独立学习能力和养成良好的学习习惯，对于发展高中学生的才能具有重大意义。

[参 考 文 献]

[1]张巧文.多元智力观对作业设计的启示[J].广西教育学院学报，2004（3）.

[2]宋秋钱.有效作业的实施策略[J].教育理论与实践，2007（5）.

（责任编辑：张华伟）