基于MATLAB 的U 型滑道输送链运动学分析

李英杰，洪 林，尹瑞华

(1.天津理工大学机械工程学院，天津 300384;2.天津商业大学机械工程学院，天津 300134)

0 前言

链传动作为机械传动中的一种重要的运动传递方式，因其经济可靠以及良好的传动性能而广泛应用于运输、采矿、冶金、军事等各种机械的传动系统中［1］。对用于低速重载输送机一类装备的链传动，因为每个链节上都带有很重的负载，重力会产生很大的拉应力，所以不允许松边的存在［2］。本文通过对U 型滑道约束的输送链模型进行拆分求解，对各拆分的模型机构进行运动学分析，重点分析输送链过渡区域的传动性能，得出各个构件的运动曲线。

1 U 型滑道输送链等效物理模型

图1为U 型滑道输送链的等效物理模型，根据各个构件的运动规律，将U 型滑道输送链的机构模型拆分成三个子机构:主动链轮啮入区域、补偿轨迹区域以及从动链轮啮出区域，这三个子机构的自由度均为1，均是组合式串联物理模型的附加机构。先对运动学分析的机构构件进行一些假设:(1)所有构件均视为刚性体;(2)滑动摩擦力和各个销轴的铰接点的非定向摩擦矩均忽略不计;(3)链节的质心在其所在链节两端销轴连线的中心处。

如图1 所示，主动链轮啮入区域链节开始啮合时，补偿段区域开始释放冗余量，然而当主动链轮啮合链节运动到某位置时，补偿段区域将产生的冗余量进行储存。

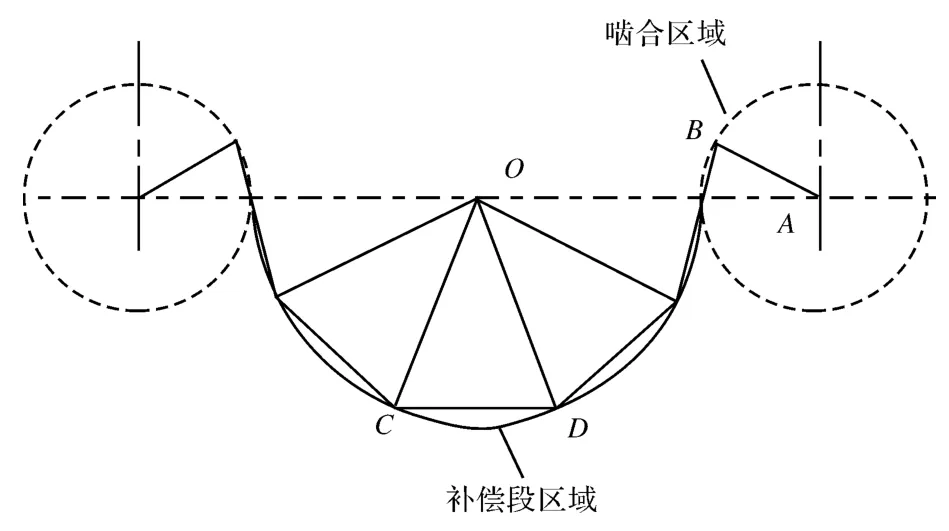
图1 U 型滑道输送链的等效物理模型Fig.1 Equivalent model of U-type slide conveyor

2 U 型滑道输送链运动学建模

2.1 主动链轮啮入区域运动学建模

将主动链轮啮入区域子机构可以等效为曲柄摇杆机构，机构的曲柄旋转角度为π/2(销轴在主动轮上的运动周期为π/2)，等效后的传动机构物理模型如图2。机构中r1～r4分别为机架的长度、曲柄的长度、连杆(链节)的长度以及摇杆的长度，且各杆件的长度、初始位置角度、曲柄的角速度ω2已经给出。

图2 主动链轮啮入区域的等效物理模型Fig.2 Equivalent model of active sprocket meshing area

建立该机构的角位移闭环矢量方程［3］

将该角位移矢量方程分别在x 轴和y 轴上进行分解

将式(2)对时间t 求取一阶导数，并整理成矩阵形式，可以得到机构的角速度方程

将式(3)分别对时间t 求取二阶导数，并整理成矩阵形式，可以建立机构的角加速度方程

2.2 位置补偿区域运动学模型

链节在补偿段区域内的运动轨迹比较特殊，将其等效成曲柄滑道机构(如图3)。曲柄滑道机构是典型曲柄摇杆机构的一种变形，将摇杆改变成弧形滑块，机架做成弧形滑槽，滑块在弧形滑槽内运动，滑槽的半径等于摇杆的长度［4］。曲柄滑道机构能形成比较不规则的轨迹，而此机构正适用于补偿段区域分析。

图3 补偿段区域的等效物理模型Fig.3 Equivalent model of compensation area

已知曲柄AB 的长度，连杆BC(链节)的长度、滑块C 的运动轨迹离散坐标点(xci，yci)，曲柄AB 及滑块C 的初始位置角度θ1和θ2。建立该机构角位移闭环矢量方程

将该角位移矢量方程分别在x 轴和y 轴上进行分解

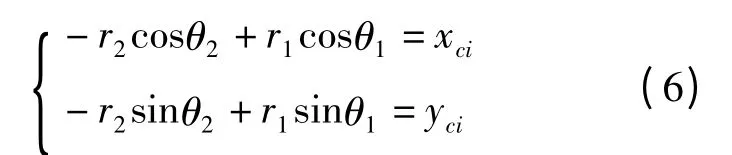
将式(2)对时间t 求取一阶导数，并整理成矩阵形式，可以得到机构的角速度方程

将式(3)分别对时间t 求取二阶导数，并整理成矩阵形式，可以建立机构的角加速度方程

2.3 从动链轮啮出区域运动学模型

与主动链轮啮入区域的等效模型类似，如图4 所示，OP为曲柄(长度为R)，PQ为啮合链节(长度为L)，QR为从动链轮的半径(长度为r)。

图4 从动链轮啮出区域等效模型Fig.4 Equivalent model of passive sprocket existing area

对图4 所示的等效物理模型建立闭环矢量方程

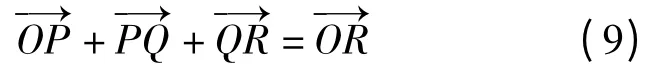
将式(9)分别在所建立的直角坐标系投影得到两分量形式

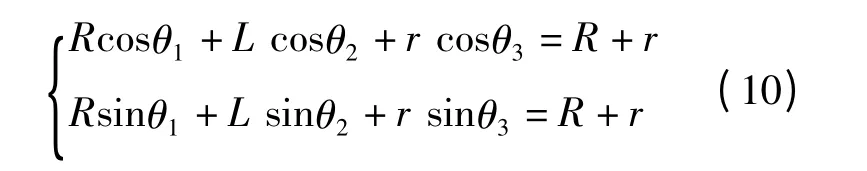
将式(10)对时间t 求取一阶导数，并整理成矩阵形式得到该机构各杆件的角速度

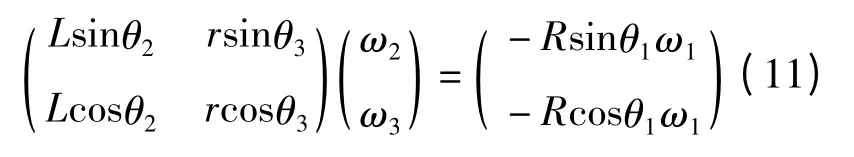
在上式中，曲柄的角速度为ω，角速度值可以由各时刻曲柄所处的位置角近似求得。

将式(10)对时间t 求取二阶导数，并整理成矩阵形式得到该机构各杆件的角加速度

3 基于MATLAB 的仿真结果

采用牛顿—辛普森方程求解机构位置非线性方程函数文件进行求解的方法，在MATLAB中建立M 文件将非线性方程组编程子程序，在一个运动周期内循环调用牛顿—辛普森方程。主动链轮以ω2=ω1匀速转动，从0°转到90°后停止，可以依次求解并得到啮合链节BC 的后节点90 个位置点的角位移结果，进而求得所有的运动参数(角速度、角加速度)。求解补偿段区域的运动参数需要知道滑块C 的速度、加速度，由于已知滑块C 的轨迹离散点坐标，很容易解出滑块C 的速度计加速度，求解方法即通过对已知滑块C 的轨迹点进行多项式拟合，得到拟合曲线的数学方程描述，将得到的方程对自变量求取一阶导数，可以得到滑块C 的速度，而对方程求取二阶导数时可以得到滑块C 的加速度。绘制出的随主动链轮运动的各个机构构件仿真结果如图5～7 所示。

图5 主动链轮啮入区域仿真结果Fig.5 Simulation results of active sprocket meshing area

图6 补偿段区域仿真结果Fig.6 Simulation results of compensation area

图7 从动链轮啮出区域仿真结果Fig.7 Simulation results of passive sprocket existing area

从角位移线图中可以看出，摇杆3(销轴C)的角位移曲线变化并不是很大，但是事实上并非如此。在角速度线图中可以看到销轴C 的角速度具有微弱的周期性波动，却比传统型的链传动机构传动性能稳定很多。

由滑块C 的运动轨迹推导出的补偿段区域内各构件的运动规律可以看出，无论是曲柄AB(前销轴)还是啮合链节BC 的角位移均变化较为平稳，其角速度及角加速度波动也不是很大，可以认为链节可以在补偿段区域内能平稳运动。

4 结论

本文利用闭环矢量法建立U 型滑道输送链的两区域的运动学模型，采用牛顿—辛普森方程求解机构位置非线性方程函数文件进行求解的方法求解出各个构件的运动参数，在一个周期内的仿真结果显示补偿段区域内的构件的角位移变化平稳，速度、加速度波动较小，能实现平稳运动，而在主动链轮啮入区域的构件波动相对较大，与传统型链传动性能相比则有很大提高。本文运动分析的结果为U 型输送链的动力学分析及速度补偿奠定有利的基础。

［1］李晓，洪林，李德胜.链传动多边形效应的一种补偿方法［J］.天津理工大学学报，2008，24(1):11－13.

［2］Weihua Liu，Yubin Gao.Compensation of Variable Pitch Roller Chains for the Polygon Effect［J］.International Conference on Electronic ＆ Mechanical Engineering and Information Technology［C］，2011:2900－2903.

［3］郭仁生.机械工程设计分析和MATLAB 应用［M］.北京:机械工业出版社，2011.

［4］赵匀.机构数值分析与综合［M］.北京:机械工业出版社，2005.

［5］唐宾，时胜德.拨禾轮偏心曲柄滑道机构的研究［J］.农机化研究，2011，11(11):93－95.

［6］刘成耀.基于Matlab 的铰链四杆机构仿真分析［J］.长江大学学报(自然科学版)，2011，8(3):109－110.

［7］赵匀.农业机械计算机辅助分析和设计［M］.北京:清华大学出版社，1998.

［8］于红英，赵彦微，许栋铭.平面铰链四杆机构的轨迹综合方法［J］.哈尔滨工业大学学报，2015，47(1):40－47.

［9］王德伦，肖大准，刘健.平面铰链四杆机构的运动几何学模型［J］.大连理工大学学报，1993，33(4):438－443.

［10］PIEGL L A，TILLER W.Surface approximation to scanned data［J］.The visual computer，2000，16(7):386－395.