对圆形线材轧扁过程中轧制力公式的研究

陈帅彰，孙斌煜，王 龙，崔鹏鹏，宋 黎

(太原科技大学重型机械教育部工程研究中心，山西 太原 030024)

0 前言

在现代计算机控制的型材生产中，轧制力设定是一个及其重要的环节，它是型材连轧精轧机组计算机设定模型的核心［1］，其设定精度直接影响到辊缝的设定，进而影响型材轧制时的稳定性及尺寸精度从而影响最终的质量。因此研究型材轧制过程中精轧机组的轧制力设定模型，提高轧制力设定精度是非常必要的。扁钢丝做为一种型材被广泛应用来制造弹簧，活塞环，扁平导线和医用导管以及其他产品。近年，传统金属极惰性气体保护电弧焊(GMAW)中用扁钢丝代替传统的钢丝电极已经成功［2］。然而高精度的扁钢丝的轧制过程中的变形相对板带轧制其变形为不均匀变形，难以用精确的计算模型对其求解。目前为止国内外很少有对轧扁过程的轧制力计算公式进行研究的。本文尝试用在板带冷轧中应用广泛的斯通公式来计算扁钢丝轧制过程中的轧制力问题。

1 斯通公式进行轧制力P 计算

轧制力计算公式为

式中，pm为平均单位压力(MPa);F为轧辊与轧件的接触面积(mm2)。

此处冷轧过程用斯通(Stone)公式进行计算平均单位压力pm

冷轧状态下的变形抗力仅与总变形程度有关，相关公式如下:

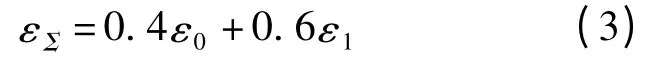
式中，ε0为本道次入口处的总变形量;ε1为本道次出口处的总变形量。

式中，μ为摩擦系数;l为轧件与轧辊接触弧长度(mm);hm为轧件平均高度(mm)。C为常数，mm3/N;γ为轧辊的泊松比，E为轧辊的弹性模量。

此处非线性方程可由数值迭代法在C 语言编程中进行迭代计算。

由上可算出式(2)中pm的值。

式中，l为接触弧的水平投影(mm);B0为轧制前轧件宽度(mm);B为轧制后的轧件宽度(mm)。

根据M.Kazeminezhaod 所研究的宽展［4］公式如式10

由式(10)可在轧件宽度B 已知的情况B0。

由以上内容便可求出轧制力P。

对以上斯通公式计算过程采用数值迭代方法并用C 语言进行编程制作轧制力计算软件如图1所示。

图1 轧制力计算软件Fig.1 Rolling force calculation software

2 对斯通公式计算过程进行分析优化

由斯通公式计算过程可得出，轧制力计算分为两部分，即求单位面积压力pm和轧辊与轧件之间的接触面积F。所以如果想提高斯通公式对于轧扁过程的计算精度应从两方面考虑。

2.1 首先考虑单位单位面积压力

其计算过程中所用轧件材料的变形抗力σ是根据轧件的变形量ε 和轧件材料的变形抗力曲线求得。因为圆截面线材轧扁过程与板带轧制不同，其变形为非均匀变形即三维变形，变形量ε 的计算精度很大程度决定了轧件材料的变形抗力σ 的计算精度，从而影响到单位面积压力

在斯通公式中变形量ε 是用高度的相对压下来表示的，即

而扁钢丝的轧扁过程非均匀变形，用高度的相对压下很大程度上是失真的。因此会造成较大的计算误差。

笔者考虑用横截面积A 的相对变化来表示轧件的变形量，为区分之前用高度压下表示的变形量，此处将面积变化率表示的变形量表示为ε'。

式中，A0为表示轧前的轧件的横截面积(mm2);A1为表示轧后的轧件的横截面积(mm2)。

本文采用上文实验数据对横截面积进行计算，轧件原始横截面积A0为19.634954mm2。各压下对应横截面积及变形量如表1。

表1 各压下情况下横截面积相对变形量Tab.1 cross-section relatively deformation under each pressure

为了更便捷的计算ε'，本文尝试用运用MATLAB 软件对几个轧件的横截面积相对变形量的值与轧件高度压下的关系进行多项式曲线拟合，拟合曲线如图2 所示。

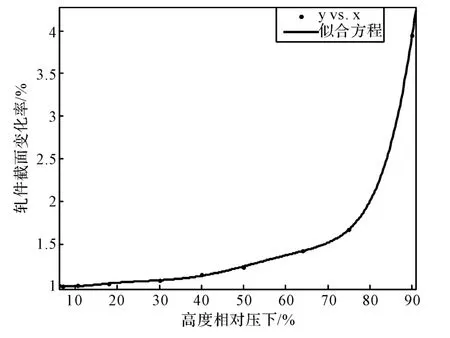
图2 面积相对变形量与高度压下的关系的拟合Fig.2 The fitting for the deformation of area and the rolling reduction

拟合所得方程为

由此可便捷的由高度的相对压下求出轧件的横截面积的变形量ε'。进而可以由此计算变形抗力。

对于材料的变形抗力，由于本文用的是202不锈钢材料，为了便捷及精确，对202 不锈钢的变形抗力曲线进行取点拟合求出其曲线公式以便于在求得变形率ε'，方便精准的计算出其变形抗力σ。其拟合曲线公式为

对于按高度压下作为变形率的其变形抗力求解为

斯通公式计算轧制力:

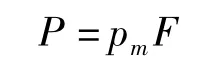
从变形率角度优化后

2.2 从接触面积角度考虑

斯通广泛应用与板带轧制中计算已经比较成熟，但是在轧扁过程中斯通公式若计算轧制力在计算接触面积的时按图3a 的形状进行计算

但是实际轧扁过程中其接触面的形状为图3b 形状，类似椭圆形。

所以由图可明显看出若按斯通公式计算则明显多算了接触面积，且接触的实际宽度如图3 所示，而不是轧件的宽度B。所以轧制力计算值偏大。导致轧制力预估不准确。

图3 接触面形状Fig.3 Contact surface shape

本文中假设扁钢丝轧制过程中的轧辊和轧件的接触面为椭圆，设接触区域的的长度(考虑弹性压扁)为I'为椭圆的长半轴，则接触宽度的一半b/2 短半轴的。所求接触面积:

而在斯通公式中所求面积为式(9)。

比较式(16)、(9)可明显看出接触面积按不同算法相差很大。因此会导致计算结果误差很大，虽然接触区域可能不是椭圆形但是非常接近，已经很大限度的提高了计算精度。

然而扁钢丝由圆形截面变为扁形截面区别于板带轧制中的变形，板带轧制过程金属变形为二维变形而扁钢丝轧扁过程为三维变形，其变形为不均匀变形。扁钢丝轧制变形过程如图4所示。

图4 线材尺寸示意图Fig.4 Wire size diagram

图4 中轧辊与扁钢丝接触区宽度可根据M.Kazeminezhad 对于扁钢丝横截面的研究求解［5］如下

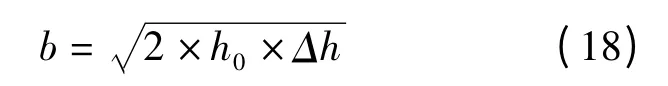
由上可得轧制力求解参数b 的大小。

常用计算公式算得P 与改进型算法的P'进行比值，只是接触面积的比较，则接触面积优化系数S 计算公式如下:

此处假设不考虑变形率问题，即p'm=pm

所以优化后的轧制力:

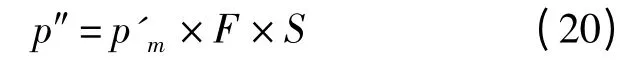
式中，S 的值是随压下变形的变化而变化的。

3 有限元模拟及实验研究

3.1 建模分析

本文用有限元数值分析软件DEFORM 中对扁钢丝轧制过程进行模拟。在DEFORM-3D 中的SHAPE ROLLING 中建立四分之一模型如图5 所示，其中轧辊直径为100 mm，轧件直径为5 mm，设置推块将轧件推入，辊缝设置为4.65 mm、4.475 mm、4.1 mm、3.4 mm、3.0 mm、2.5 mm、1.8 mm 进行边界条件施加和载荷施加:

图5 轧扁四分之一模型示意图ig.5 A quarter of the model for the flattening a quarter

(a)轧辊与轧件之间的摩擦统一设定为昆仑摩擦，摩擦系数为0.08。

(b)推块的速度为100 mm/s。

(c)轧辊的转速为3 rad/s，即0.15 m/s。

(d)设定步数为250 步，步长为0.00225 s。

(e)设定速度误差为0.005 mm/s，力的误差为0.05 N。

对模型进行数值计算，轧后示意图如图6 所示。提取轧制力进行分析。

图6 压下64%轧扁效果示意图Fig.6 Press down 64% flatting effect diagram

3.2 结果比较:

对于扁钢丝的轧制过程分别用斯通公式、优化后公式进行计算。然后进行Deform 数值模拟分析进行轧制力提取，和试验提取。进行结果比较分析。数据见表2。

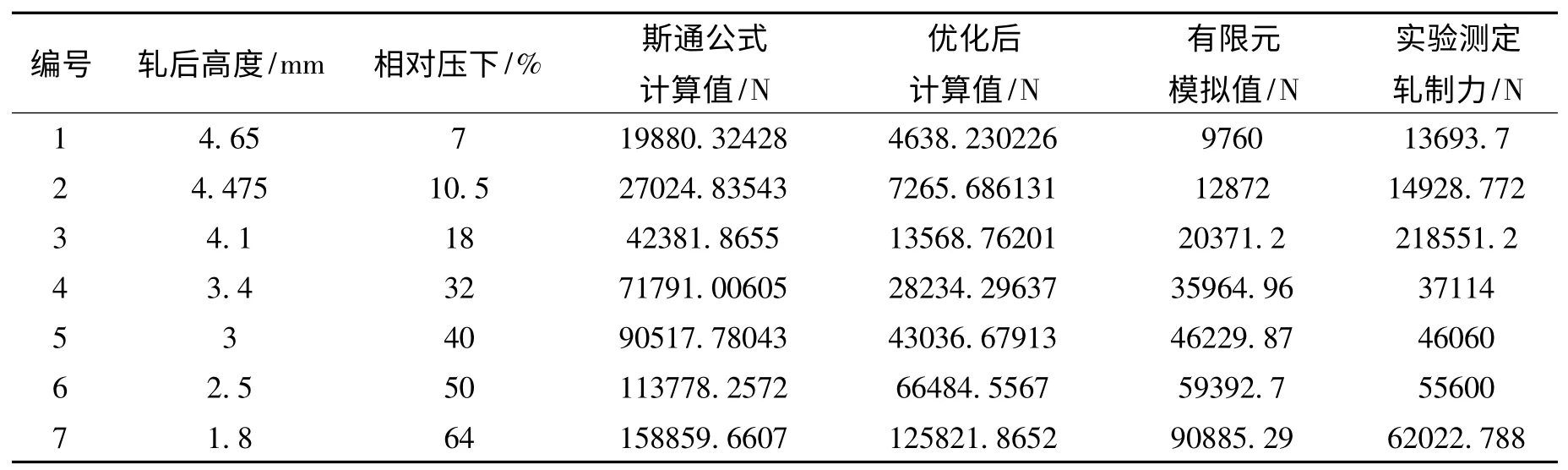
表2 数据处理Tab.2 data processing

理论计算与模拟及实验中所得轧制力如图7表所示。

图7 四种轧制力值的对比分析图Fig.7 Four kinds of rolling force value contrast analysis diagram

3.3 对结果进行比较分析

由图7 可看出，在优化前的轧制力计算值相比较实验值、模拟值、和优化后的计算值误差较大，且计算值大大超出其他值，所以相对于原斯通公式计算值优化效果明显。优化后公式的轧制力计算值相比于有限元数值模拟值和实验测定值较小，但误差相比于优化前大大降低。由图还可得出，优化后的计算值在较小相对压下率情况下如7%、10.5%、64%时，其计算值与模拟值和实验值误差较大，而在30%～50%压下情况下其计算误差能控制在15%之内，这是在轧制力计算时可以接受的范围，所以可以知道优化后的轧制力计算公式比较适用于轧扁过程的中度压下，而较小压下和较大压下情况下其计算偏差较大，分析其原因可能是因为在较小和较大压下情况下所用宽展预测公式可能不适用，造成误差。这正验证了圆形截面线材的扁平化轧制过程是不均匀变形，其变形为3D 变形，在中度压下情况下误差较小说明说明其变形趋于均匀，即压下加大情况下其变形趋于均匀，但是在较大压下情况下，例如64%压下时，其计算公式中应用到的宽展公式可能不太适用，所以造成计算值较大超出模拟值及实验值。

由图7 可清楚看到数值模拟所得轧制力数值与实验所测数值在7%～50%之间误差很小，说明实验效果和模拟效果很好，Deform 能够很精准的对轧制过程进行数值模拟。但是在7%压下和64%情况下，Deform 的数值模拟值与实验值有一定误差，分析其误差原因，在7%压下时，可能是实验所用轧机的传感器由于使用时间较长，在小轧制力作用下其应变片应变效果不太明显，所以其轧制力显示较大，在64% 压下时，其轧制压下过大，而轧辊直径偏小，其咬入困难，轧机提供的动力难以进行轧制，以达到最高轧制力，且在实验过程中也是试件轧制进行到一半的时候轧机无法转动进行轧制，其轧制力是取其已轧制区段的轧制力，所以实验值小于模拟值，且相差较大。

4 结论

线材轧制过程为冷轧，斯通公式广泛应用于冷轧。本文对斯通公式进行优化，首先对影响变形抗力σ 的轧件变形率ε 进行优化，用轧制前后的截面积表示变形率ε'，从而更精准的得到轧制时的变形抗力。其次对轧件与轧辊的接触表面形状做椭圆假设，使其所求接触面积更加接近实际值，并推导出接触面积影响系数S。

通过对轧制过程的数值模拟及实验得出:优化后的轧制力计算公式P″=P'm×F ×S，相比优化前的计算精度大有提升，但是在较小(如10.5%及以下)及以下和较大(64%及以上)压下时误差较大，在中度压下时计算精度较高。

［1］胡建军，李小平.DEFORM-3D 塑性成形CAE 应用教程［M］.北京:北京大学出版社，2012:183－184.

［2］C.Vallellano，P.A.Cabanillas.Analysis of deformations and stress in flat rolling of wire［J］.Journal Materials Processing Technology，2008，(195):63－71.

［3］邹家祥.轧钢机械［M］.北京:冶金工业出版社，2007:49－53.

［4］M.Kazeminezhad，Karimi Taheri.A theoretical and esperimental investigation on wire flat rolling process using deformation pattern［J］.Mater.Design，2005，(26):99－103.

［5］M.Kazeminezhad，Karimi Taheri，A.Kiet Tieu .A study on the cross-sectional profile of flat rolled wire［J］.Journal Materials Processing Technology，2008，(200):325－330.