一种时序约束下的Web服务组合兼容性的定量验证方法

郑宇迪，叶恒舟

(桂林理工大学信息科学与工程学院，广西桂林541004)

作为一种基于现有互联网协议与公开标准的自包含、自描述、模块化的应用，Web服务成为设计复杂商务应用的主要技术之一，而服务组合是研究服务技术的关键之一。为了增强服务组合的正确性及QoS特性，在流程设计层面的时间约束下的兼容性验证与错误检测正受到越来越多的关注。

当前，已经出现了一些验证组合服务的时序约束兼容性研究成果，如徐红霞等[1]提出了一种有限状态机(finite state automaton，FSA)模型，讨论了服务路径中顺序、选择、并行和循环4种结构的兼容性推导过程，并针对时序部分兼容的服务组合，提出相应的时序兼容性修正方法。为了缓解兼容性验证中广泛存在的组合爆炸问题，文献[2]将服务组合的时序约束分为两个层面，即服务内部的时序约束及服务之间的时序约束，并分别采用时序开放工作流网络(timed open workflow net，ToN)和协调网络(mediation net)表示，最终构建出模块化时序状态图(modular timed state graph，MTSG)，进而分析时序约束的兼容性。当两类约束均衡分布时优化效果较为明显。线性时序逻辑(linear temporal logic)[3]、活动时序逻辑(temporal logic of actions)[4]等模型检测方法也被用来描述服务组合中的各种时序约束，并进行兼容性验证。

以上研究认为单个活动的执行时间是固定值或区间，因而只能定性验证组合服务的时序约束兼容性(完全兼容、完全不兼容、部分兼容)。为此，文献[5]提出了一种基于概率的时序兼容性检验方法，以定量分析服务的兼容程度，但它通过转化并行与选择结构为顺序结构的形式回避了并行与选择结构的影响，而这种转换不仅容易导致组合爆炸问题，也不容易自动处理。笔者假设活动的时序约束符合正态分布，通过讨论顺序、选择及并行3种结构的概率分布，提出了一种基于概率的定量检验服务的时序兼容性的方法。本文的主要贡献是提出了一种估计两个正态分布随机变量的最大(小)值分布的算法，进而估算组合服务的时间分布，定量估计其时序兼容性。

1 时序工作流模型

Petri网[6]常用来描述服务及其组合。

定义1(工作流网，WFN)有向网PN=(P，T，F)是WFN的充要条件为:(1)PN有一个源库所i∈P，使·i=∅;(2)PN有一个漏库所o∈P，使=∅;(3)每个节点x∈P∪T都属于从i到o的一条路径上。

T中的变迁代表工作流中的活动，活动之间的依赖关系F通过库所的连接表示。多个活动可能顺序执行、并行执行或选择其中一个执行。为了讨论方便，约定由两个或以上活动顺序(并发、选择)组成的结构块称为纯顺序(并发、选择)结构块(图1)。考虑到不受约束的WFN可能导致潜在错误且不易发现与改正[7]，本文讨论的WFN仅由有限个纯顺序、并发或选择结构块嵌套形成，即非顺序结构块不允许交叉。

定义2(时序工作流网，TWN)一个时序工作流网是一个五元组TWN=(P，T，F，X，R)。其中:

(1)(P，T，F)是一个WFN;

(2)X={x1，x2，…，xn}，xi～N(μi，)是与ti∈T关联的一个基于正态分布的非负实数值，代表ti的时间开销;

(3)R={r1，r2，…，rm}描述工作流的时序约束，rk(ti，tj)≤dk表示tj应该在ti开始后不超过dk个时间单元内结束;

一条时序约束rk(ti，tj)≤dk的时序兼容性可通过rk(ti，tj)≤dk的概率来度量，为此，需要估计rk(ti，tj)的概率分布。

图1 不同的结构块Fig.1 Different structures

2 时序兼容性检查

对于给定TWN中的每一条约束rk(ti，tj)≤dk，约定包含在ti、tj的部分(包含ti与·ti，tj与t·j在内)也是一个TWN，即也是由有限个纯顺序(并发或选择)结构嵌套形成。算法1描述了一种基于概率的自动检验TWN时序兼容性的方法。

算法1:基于概率的时序兼容性检验

输入:一个TWN及置信水平1－α

输出:时序兼容性检验结果

S1:For(TWN中的每一条约束rk(ti，tj)≤dk)

{

S2:while(包含在ti，tj的部分存在纯结构)

选择一个纯结构，计算其概率分布赋给事件t，并用t代替该结构;

S3:将最后剩下的事件的分布作为rk(ti，tj)的分布，若rk(ti，tj)≤dk的概率小于1－α，输出“不兼容”并退出;

}

S4:输出“兼容”;

算法1的基本思想是逐条检验时序约束，每条约束对应以ti开头、tj结尾的一个子TWN。检验时，先通过步骤S2由里及外的逐步替换该TWN中的纯结构，直到TWN中仅剩下1个事件，该事件对应的概率分布就是该TWN的概率分布。再通过步骤S3确认该约束是否可兼容。由于每次纯结构替换都至少减少1个事件，设TWN中包含n个事件，则S2最多执行n次。若TWN中的约束条数为m，则算法1的时序复杂度为O(n×m)。如何计算一个纯结构的概率分布是算法的关键，将在下节探讨。

3 3种纯结构的概率分布估算

设在TWN中出现的变迁ti时间开销对应一个随机变量xi，xi～N(μi，σ2i)，且xi与xj(i≠j)相互独立。

3.1 纯顺序结构的概率分布

在图1a中，当变迁t1、t2都依次激活后，整个结构的变迁才算完成。其时间开销x12应该为两个变迁的时间开销之和，即x12=x1+x2，即x12～

3.2 纯并发结构的概率分布

考虑图1b，当变迁t1完成后，变迁t2、t3可同时激活，当它们都完成后，才能激活变迁t4。设变迁t2、t3整体的时间开销为x23，整个结构的开销为x1+x23+x4，故关键在于计算x23=max(x2，x3)的概率分布。

很难列出可以表示x23的概率分布的简单数学表达式，实验测试也表明该分布并不符合常见的分布类型;但可以通过采样的方式确定x23样本的有效(考虑置信水平)分布范围，再构造一个相应的正态分布，使其具有一致的有效范围。算法2实现了这一思想，其时间开销主要由步骤S2、S3、S4决定。其中S2的时间开销由采样次数(Times)决定。测试表明，当Times取10 000时，算法2的结果已经很稳定。S3、S4已经有很成熟的算法，其时间开销主要由采样密度决定，实验时采用了Matlab中的默认值。因而，算法2的时空复杂度不随问题的规模变化。

算法2:估计2个正态分布变量的最大值的分布

输入:X1～N(μ1，σ21)，X2～N(μ2，α22)及置信水平1－α

输出:μ，σ

S1:定义样本数组Examples[Times];

S2:For(i=1 to Times)

{

取X1的随机样本x1;

取X2的随机样本x2;

将min{x1，x2}存入Examples[i];

}

S3:以Examples[Times]构成分布F(y);

S4:寻找a使F(y≤a)=α;

寻找b使F(y≥b)=α;

S5:μ=(a+b)/2;

σ=(b－a)/(2*zα);//zα为标准正态分布的上

α分位点

3.3 纯选择结构的概率分布

考虑图1c，变迁t2、t3整体的时间开销x23=min(x2，x3)，可以用类似算法2的方法估算其概率分布。

尽管以上讨论是基于两个变迁的情形，对于多个变迁的情形也是适用的。

4 实例分析与性能测试

4.1 实例分析

某单片机系统开发流程可以用如图2所示的TWN描述，其中变迁t1～t8分别表示“系统需求分析”、“主板设计”、“软件架构设计”、“外设设计”、“重构已有系统”、“重新开发新系统”、“软件测试”、“集成测试”，对应的时间开销依次服从正态分布N(16，4)、N(6，2)、N(4，1)、N(8，2)、N(4，2)、N(6，1)、N(8，2)、N(10，3)。

为了估计整个TWN的时间开销分布(采样次数为10 000，α=0.01)，首先转化由路径p2到p5的纯顺序结构，转化的效果为图3a，其中t24的分布为N(14，4);再转化由路径p3到p10的纯选择结构，转化后如图3b所示，其中t37的分布为N(15.5，6.9);最后转化由路径p1到p11的纯并发结构，转化的效果为图3c，其中t18的分布为N(42.4，16.7)，即整个TWN的时间开销分布。

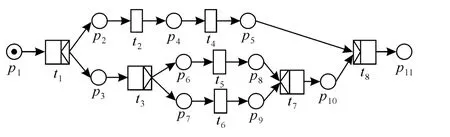
图2 用TWN描述的某系统开发流程Fig.2 System development describted by TWN

4.2 性能测试

为了测试估算的概率分布的有效性，设某TWN的时间开销的随机样本值为{x1，x2，…，xn}，其估算的概率分布服从N(μ，σ2)，统计样本值位于区间[μ－zασ，μ+zασ]的个数与n的比值称为命中率，命中率越高，表明估算值越有效。当样本总数为10 000时，上例的命中率约为99.5%(α=0.01)、98.5%(α=0.02)、94.0%(α=0.05)或87.4%(α=0.1)，可见当置信水平较高时，具有很高的命中率。

图3 TWN的转化过程Fig.3 Process of TWN transformation

在估算两个正态分布的最大值或最小值的分布函数时，这两个正态分布的概率密度曲线重叠部分的大小影响估算的准确性。为此，根据t5与t6的时间开销概率密度曲线重叠部分的面积差别，为t5与t6取了一组测试值。测试结果表明，不同取值时的命中率变化不大且均接近95%(表1)，验证了该方法的有效性与稳定性。

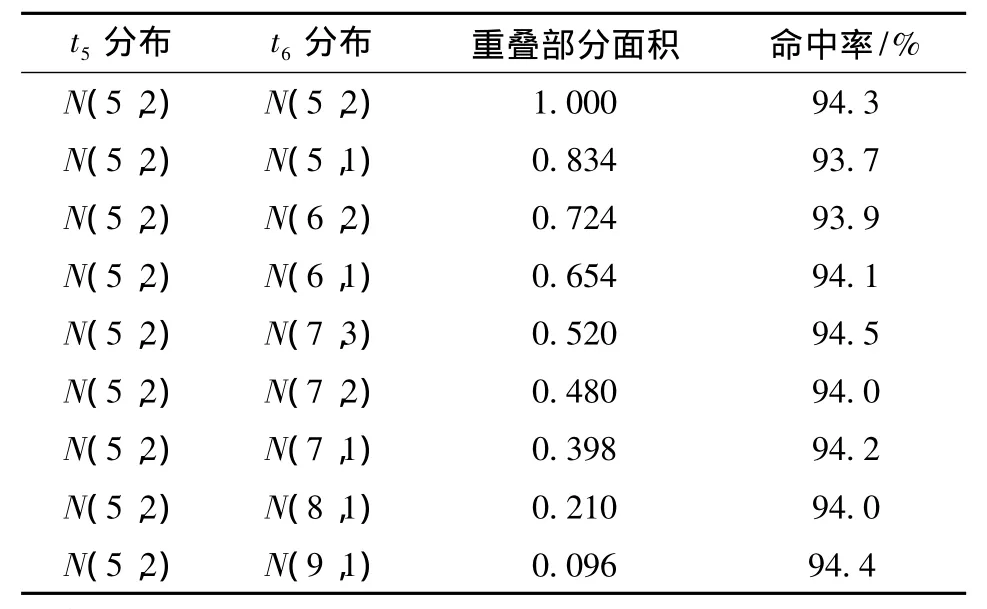
表1 不同取值时的命中率Table 1 Hit rates with different values

5 结论

时序约束是支持QoS的服务组合的一个重要指标，然而单个活动的时间开销往往并不容易准确指定，组合服务的时序兼容性也并不总能严格满足，因而需要研究一种基于正态分布和可信度的组合服务时序约束兼容性检验方法。笔者提出了一种基于概率的定量检验时序兼容性方法，重点探讨了纯顺序(并发及选择)结构的概率分布估算方法。实例分析与性能测试表明该方法是可行、有效的。下一步的工作目标是将相关算法应用于动态Web服务选择，研究高效的、支持时序约束的动态Web服务组合方法。

[1]徐红霞，杜彦华，董绍华.时序约束下Web服务组合的兼容性及修正研究[J].计算机集成制造系统，2012，18(11):2562－2572.

[2]Du Y H，Tan W，Zhou M C.Timed compatibility analysis of Web service composition:A modular approach based on Petri nets[J].IEEE Transactions on Automation Science and Engineering，2014，11(2):594－606.

[3]Hao S G，Zhang L.Dynamic web services composition based on linear temporal logic[C]//IEEE Computer Society.2010 International Conference of Information Science and Management Engineering(ISME)，2010:362－365.

[4]Wang H B，Zhou Q Z，Shi Y Q.Describing and verifying web service composition using TLA reasoning[C]//IEEE Computer Society.2010 International Conference of Services Computing(SCC)，2010:234－241.

[5]Du Y H，Wang X F，Yao J S.Probability based timed compatibility of Web service composition[M]//Practical Applications of Intelligent Systems.Berlin，Heidelberg:Springer，2012:31－39.

[6]Du Y H，Xiong P C，Fan Y S，et al.Dynamic checking and solution to temporal violations in concurrent workflow processes[J].IEEE Transactions on Systems，Man and Cybernetics，Part A:Systems and Humans，2011，41(6):1166－1181.

[7]Son J H，Kim M H.Improving the performance of time-constrained workflow processing[J].The Journal of Systems and Software，2001，58(3):211－219.