基于梯形网格辛Runge-Kutta射线追踪的角度域层析偏移速度分析
魏亦文,熊彬,唐国彬
(桂林理工大学a.地球科学学院;b.广西矿冶与环境科学实验中心,广西桂林541004)
复杂构造区采集的低信噪比地震数据经过偏移后生成的共成像点道集(CIGs)比原始数据显得简单些,可将旅行时反演与偏移速度分析(MVA)组合为层析偏移速度分析方法(TMVA),将波动方程层析反演和MVA组合成波动方程偏移速度分析法(WEMVA)。研究和实践表明,在成像空间中,针对速度比不大的地下结构成像和偏移速度建模,TMVA比WEMVA的应用更普遍。在考虑构建TMVA的反演线性方程组问题时,剩余时差和偏导数矩阵的求取是最关键的问题。
叠前深度MVA是建立复杂介质速度模型的有效工具。Faye等[1]提出深度聚焦分析(DFA);Al-Yahya等提出剩余曲率分析(RCA),利用剩余校正(RMO)来确定速度误差,CIGs平直性来判断速度模型的正确性[2];Berkhout等提出共聚焦速度分析(CFP),然后对其进行推广应用[3];Stork等基于RCA理论将反射旅行时反演应用到MVA中,提出TMVA[4]。
采用Kirchhoff偏移作为引擎的MVA,生成的CRP道集可能存在假象,利用DSRWDC或RTM提取的ADCIGs被证明是没有假象的道集。Prucha等采用DSRWDC生成ADCIGs[5],并将其应用于速度分析;Clapp等利用反射层位约束,基于ADCIGs实现了TMVA[6];Biondi等分析了ADCIGs的运动学特征,推导了求取RMO和旅行时残差的公式[7];Sava等提出了时移成像条件,通过倾斜叠加得到时移角道集并用于偏移速度分析[8];刘守伟等基于时移ADCIGs,提出将DFA和RCA两种方法进行组合求取偏移速度模型[9];张敏等对各种道集进行对比分析指出ADCIGs最适合MVA[10];秦宁等实现了自动拾取的成像空间走时反演速度模型[11]。研究表明,复杂构造中ADCIGs与偏移速度模型之间的关系比较复杂,确定两者之间的关系是角度域层析反演的基础。
本文实现了在角度域更新层速度模型的TMVA方法:①通过常规速度分析获得矩形网格初始层速度模型,在此基础上采用DSRWDC提取ADCIGs;②求取ADCIGs的RMO并计算旅行时残差作为层析反演线性方程组的右端;③根据初始速度模型和偏移层位构建梯形网格速度模型,在此基础上采用辛Runge-Kutta射线追踪算法构建方程组左端的偏导数矩阵;④建立TMVA处理流程,对青海某工区实际地震资料进行处理,验证该方法的可行性和有效性。
1 角度域层析偏移速度分析
1.1 角度域层析反演方程
角度域层析反演是在ADCIGs基础上构建旅行时反演方程
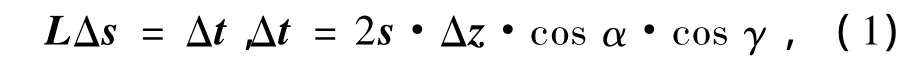
其中:L是灵敏度矩阵;Δt是走时残差;Δz是ADCIGs的剩余深度;Δs是慢度更新;α是地层倾角;γ是反射角。Δz可以通过ADCIGs剩余曲率选取控制点自动拟合求解,具体步骤见文献[11];式(1)中Δt具体推导见文献[7]。
为高效求解最小二乘法(LSQR)正规方程,数据量不大时直接采用GPU-LU或者递归LU[12-14],数据量很大时采用矩阵压缩存储技术和并行算法[13]。
1.2 DSRWDC提取ADCIGs
单程波方程波场向下延拓包括炮域单平方根方程波场向下延拓和CMP域双平方根方程波场向下延拓(DSRWDC)[8,15-16],两种方法提取ADCIGs效果相同。本文选取DSRWDC提取ADCIGs,将波场变换到频率域沿深度方向向下延拓,对频率求和相当于取零时间成像条件,得到局部半偏移距共成像点道集(ODCIGs)。速度模型正确时ODCIGs能量应该聚焦在零偏移距处,否则不聚焦。为利于RCA速度分析,利用文献[16]中的方法将ODCIGs快速转化为ADCIGs,算法的实现调用了美国Stanford大学勘探项目组(SEP)开发的SEPlib库。
1.3 初始速度模型梯形网格参数化
常规MVA方法可以获得旅行时反演需要的初始速度模型,主要包括叠加速度分析、Dix层速度反演、Kirchhoff MVA[17-18]。矩形网格速度模型通过层位控制插值后可以转换成梯形网格[12],图1是Zelt C等提出速度模型的梯形网格参数化方式,每个梯形单元的上下两条边具有不同的斜率k1、k2和截距b1、b2,但左右两条边必须是垂直的,x1、x2分别表示梯形网格左侧和右侧边界横坐标。可以利用梯形单元的4个节点速度或慢度(速度的倒数)插值得到梯形单元内任何位置的速度或慢度值。本文计算中梯形单元4个节点是慢度s1、s2、s3、s4,梯形单元内的任意点慢度值沿着梯形的4个边都是线性变化的,因此在梯形单元中存在水平慢度梯度或者垂直慢度梯度。地层界面可以用梯形网格上下界面连接组成,为计算界面的斜率需要对界面节点进行三次样条插值平滑处理[14],以满足射线追踪需要。梯形网格速度建模利用了构造信息,因此它更符合地质规律。
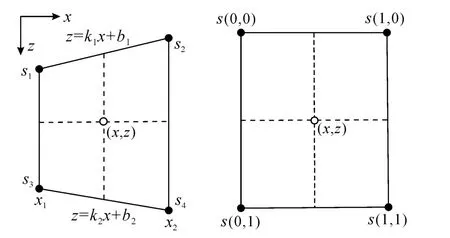
图1 梯形网格与矩形网格慢度插值示意图Fig.1 Slowness interpolation of trapezoid and rectangular grid
图1中梯形网格任意位置(x,z)处的慢度s(x,z)计算公式为
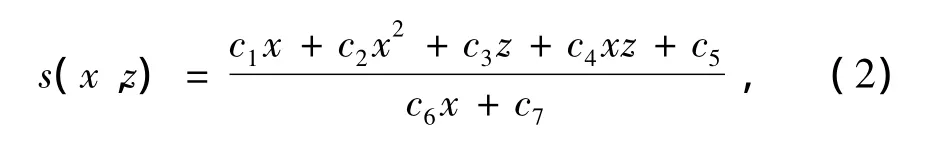
其中,系数c1、c2、c3、c4、c5、c6、c7表达式为

当s1、s2、s3、s4的4个顶点坐标分别为(0,0),(1,0),(0,1),(1,1)时,利用式(3)求取系数c1~c7并代入式(2)得
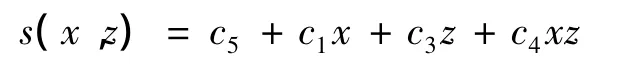
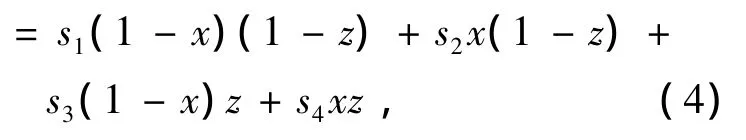
式(4)就是矩形网格双线性插值的基本公式,显然它是梯形网格双线性插值的特例。把慢度插值函数看成是4个顶点慢度si的函数,从式(3)可以看出,系数c1~c7中除了c6、c7与s1、s2、s3、s4无关外,其余均有关,由此可以得到梯形网格慢度场对4个顶点慢度的偏导数为
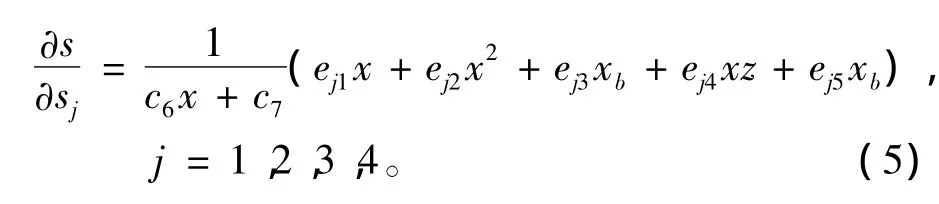
其中系数ej1、ej2、ej3、ej4、ej5的取值为
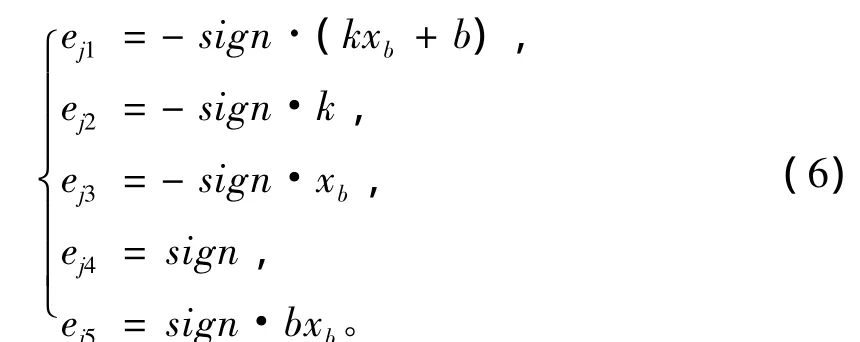
对第j个顶点来说,sign、k、xb、b是常数,见表1。
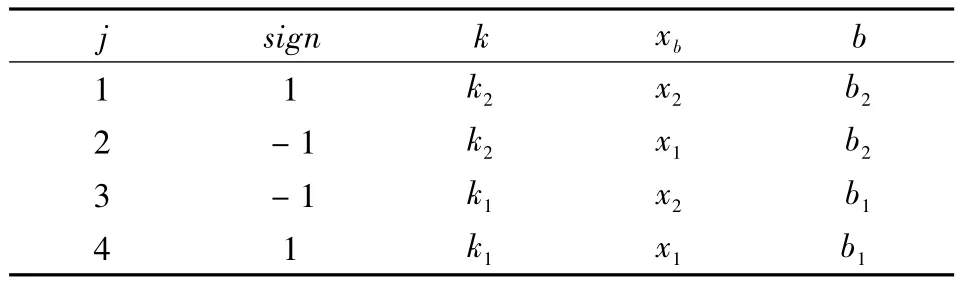
表1 偏导数中的参数值Table 1 Parameter values of partial derivative
当s1、s2、s3、s4的4个顶点坐标分别为(0,0),(1,0),(0,1),(1,1)时,根据式(2)和式(3)及表1容易证明梯形网格慢度函数s(x,y)对各节点慢度sj的导数与式(4)慢度函数对各节点慢度导数相同。
1.4 角度域辛Runge-Kutta射线追踪
Zelt C开发了RAYINVR软件,针对宽角反射射线追踪,在梯形网格中使用Runge-Kutta算法求解简化的射线追踪方程[12]。本文并不对射线方程进行简化,根据射线追踪方程一般形式,引入弧长τ得到射线追踪方程组[19-20]
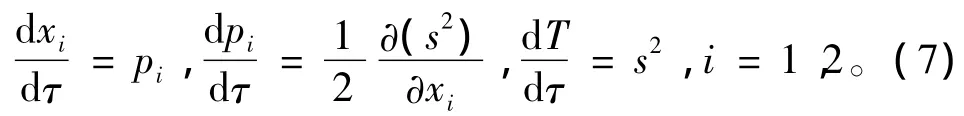
其中:x=(x1,x2)为坐标;s(x1,x2)为介质慢度分布;T为射线走时;是慢度向量,τ(T)=τ(T0)+∫Tc2dT。
式(7)为Hamilton系统,Hamilton函数为
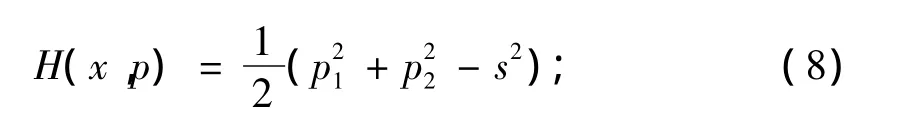
考虑Hamilton系统
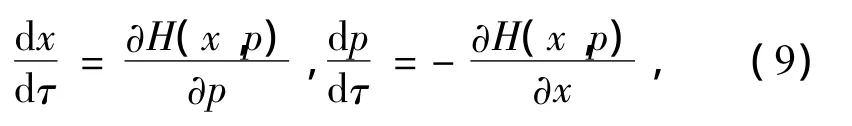
可以证明式(7)为Hamilton量H(x,p)≡0的正则方程,联合式(8)有


其中,h为步长;j为迭代次数,j=1,2,3,4。给定当前点(k(0),x(0))利用式(11)经过4次迭代计算得到下一个点射线参数和位置(k(4),x(4))。aj,bj是最优化系数参见文献[22]。
由于式(11)表示的辛Runge-Kutta算法直接在τ域计算射线路径,不需数值积分求旅行时,因此能高效求取反演线性方程组左侧的偏导数矩阵(灵敏度矩阵)。设梯形网格节点个数为N,射线有M条,式(1)中偏导数矩阵L的元素为第i(i=1,2,…,M)条射线旅行时对第j(j=1,2,…,N)个节点慢度sj的偏导数。首先,找到以sj为顶点的所有梯形单元,单元个数为K(1≤K≤4),求取每个梯形单元内射线路径,然后利用式(5)求取每个单元慢度函数对顶点sj的梯度作为权系数,最后对K个射线路径加权平均得到顶点sj对应的偏导数矩阵元素。
角度域射线追踪是从成像点向地表进行的,对于图2所示的理论速度模型,采用层位控制梯形网格参数化方式,应用式(11)进行射线追踪(图3)。

图2 理论层速度模型Fig.2 Theoretic interval velocity model
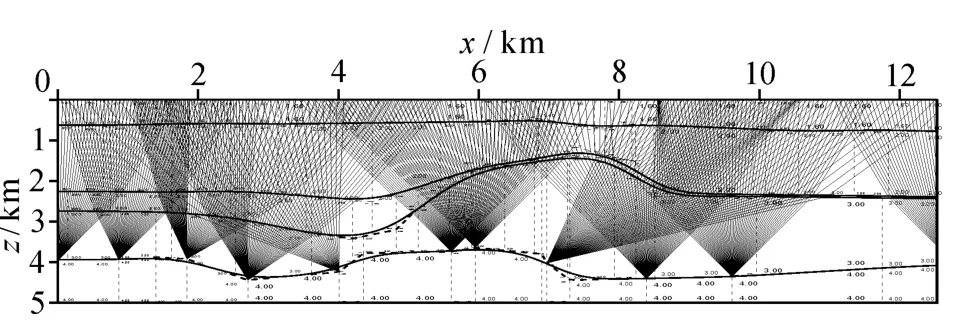
图3 辛Runge-Kutta射线追踪Fig.3 Symplectic Runge-Kutta seismic ray tracing
2 青海2-D叠前资料处理
针对青海的某2-D工区低信噪比叠前地震数据,通过前期预处理,再利用叠加速度分析、Dix反演和Kirchhoff偏移速度分析建立初始速度模型,然后应用TMVA求偏移速度模型,本文采用的速度分析处理流程(图4)。
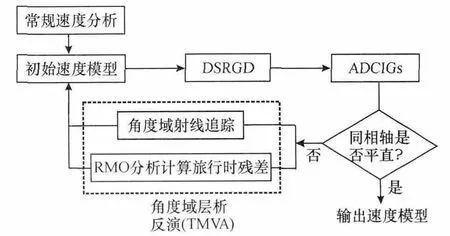
图4 TMVA流程图Fig.4 TMVA flowchart
2.1 初始速度模型
首先采用叠加速度分析求取均方根速度(RMS),然后通过最小二乘Dix反演层速度模型,再应用常规MVA求偏移速度,最后利用文献[13]中混合插值法进行圆滑得到初始速度模型(图5)。
采用Dix反演层速度模型(图5b)和Kirchhoff叠前深度偏移提取的地面偏移距共成像点道集(CIGs),CMP范围215~221的CIGs,其同相轴向下弯曲(图6a),表明偏移速度过大[9-11];图6b为偏移距范围100~1 000 m的叠加剖面。

图5 矩形网格初始速度模型Fig.5 Initial velocity model of rectanguler grids
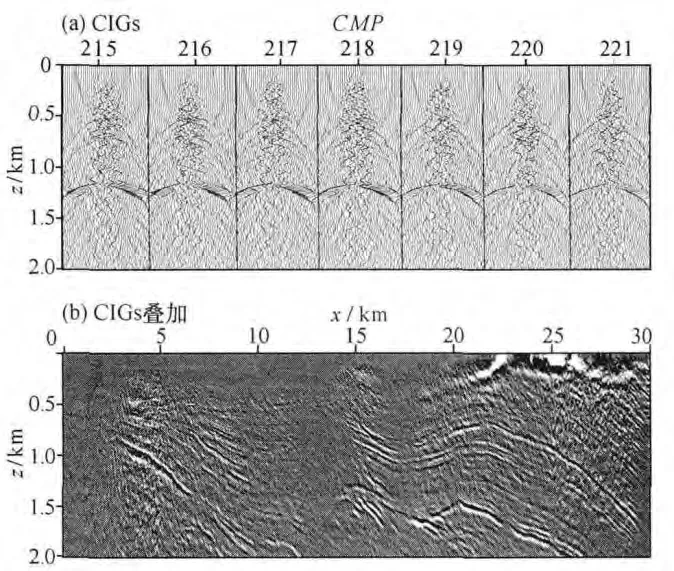
图6 Kirchhoff叠前深度偏移Fig.6 Kirchhoff pre-stack depth migration
2.2 提取ADCIGs
利用初始速度模型和DSRWDC偏移提取的ADCIGs(-30°~30°)见图7,CMP位置从722开始,间隔75,图7同相轴向上弯曲较大,表明ADCIGs中存在明显的剩余深度。对ADCIGs叠加,见图8。
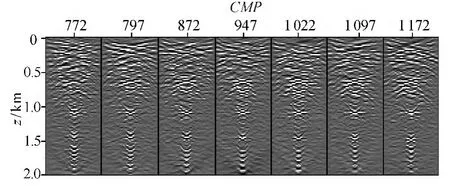
图7 初始速度模型DSRWDC提取的ADCIGsFig.7 ADCIGs extracted by DSRWDC with initial velocity model

图8 初始ADCIGs叠加剖面Fig.8 Initial stack of ADCIGs
2.3 层析偏移速度分析
利用图6b初始偏移剖面拾取层位,并根据图5c速度模型建立梯形网格速度模型(图9a),其均匀采样输出速度模型见图9b,表明速度模型符合地质规律,然后选择成像点进行射线追踪(图10)。
利用图9速度模型和TMVA迭代4次后的速度模型见图11。用DSRWDC偏移后,与图7相同CMP位置处的ADCIGs显示结果见图12,其ADCIGs小角度(-10°~10°)同相轴比图7更平直,10°以上同相轴有弯曲,为大角度数据缺失后偏移所致。对ADCIGs进行叠加(图13),与图8角度域初始叠加剖面相比,成像精度明显得到了提高,说明TMVA迭代更新后速度模型精度也得到了提高。
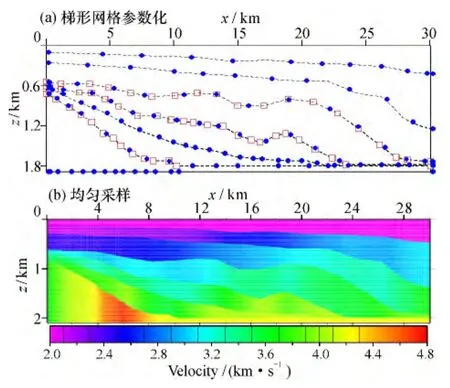
图9 初始速度模型Fig.9 Initial velocity model
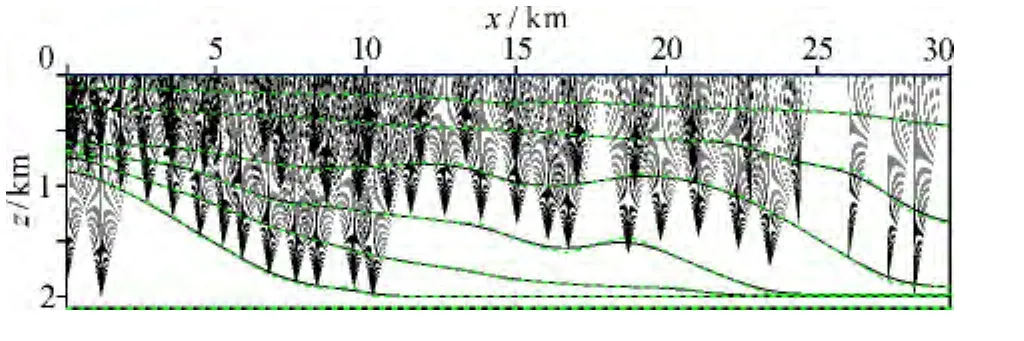
图10 角度域辛Runge-Kutta射线追踪Fig.10 Angle domain symplectic Runge-Kutta seismic ray tracing
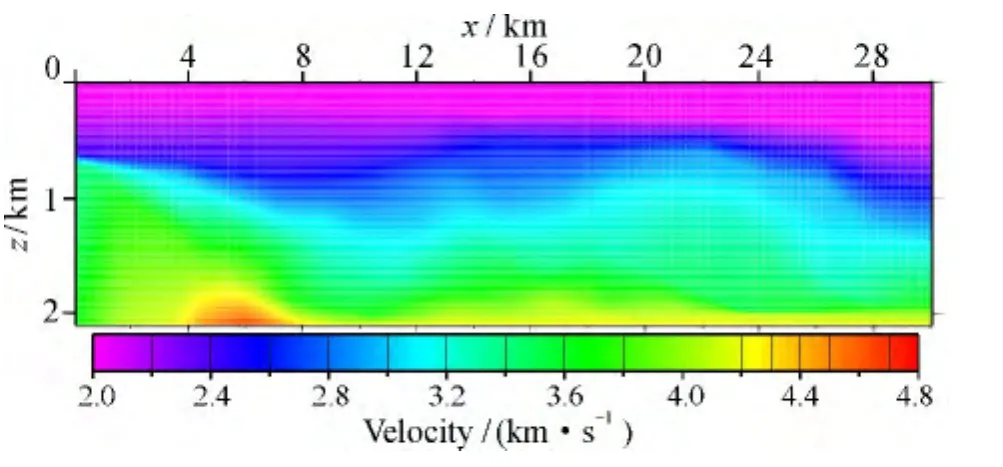
图11 4次迭代结果Fig.11 Result after 4 times iteration
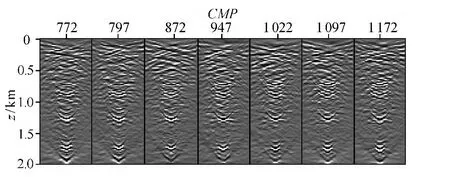
图12 最终速度模型偏移ADCIGsFig.12 ADCIGs migrated by final velocity model

图13 TMVA后角度域叠加剖面Fig.13 Angle domain stack after TMVA
3 结论
(1)对速度模型采用了梯形网格参数化方式,与矩形网格相比,可灵活选择层位控制点及速度控制点位置,且更符合地质规律。
(2)根据ADCIGs视反射角范围从成像点向地表进行射线追踪,辛Runge-Kutta算法求解τ域射线追踪方程,不需要数值积分求射线走时,只需要计算射线路径可快速求取层析反演线性方程组左侧的偏导数矩阵。
(3)在青海地震资料处理中,使用的角度域多次迭代TMVA方法建立的圆滑层速度模型比常规叠前MVA方法建立的速度模型精度更高,表明该方法是可行、有效的。
中国地质大学(北京)王彦春教授提供了地震数据,并在处理方法上给予了很好的建议,在此表示衷心的感谢。
[1]Faye J P,Jeannot J P.Prestack migration velocities from focusing depth analysis[C]//SEG 56th Annual Meeting,Expanded Abstracts,Houston:Society of Exploration Geophysicist,1986:438-440.
[2]Al-Yahya K.Velocity analysis by iterative profile migration[J].Geophysics,1989,54(6):718-729.
[3]Berkhout A J,Rietveld W E.Determination of macro models for prestack migration:Part 1 Estimation of macro velocities[C]//SEG 64th Annual Meeting,Expanded Abstract,Los Angeles:Society of Exploration Geophysicist,1994:1330-1333.
[4]Stork C,Clayton R W.Linear aspects of tomographic velocity analysis[J].Geophysics,1991,56(4):483-495.
[5]Prucha M L,Biondi B L,Symes W W.Angle-domain common-image gathers by wave-equation migration[C]//SEG 69th Annual Meeting,Expanded Abstracts,Houston:Society of Exploration Geophysicist,1999:824-827.
[6]Clapp R G,Biondi B L,Claerbout J F.Incorporating geologic information into reflection tomography[J].Geophysics,2004,69(2):533-546.
[7]Biondi B,Symes W W.Angle-domain common-image gathers for migration velocity analysis by wavefield-continuation imaging[J].Geophysics,2004,69(5):1283-1298.
[8]Sava P,Fomel S.Angle-Gathers by Fourier Transform[R].Stanford Exploration Project,Report 103,2000:123-133.
[9]刘守伟,王华忠,程玖兵,等.时空移动成像条件及偏移速度分析[J].地球物理学报,2008,51(6):1883-1891.
[10]张敏,李振春,张凯,等.叠前偏移共成像点道集的对比分析[J].地球物理学进展,2011,26(1):220-228.
[11]秦宁,李振春,杨晓东,等.自动拾取的成像空间域走时层析速度反演[J].石油地球物理勘探,2012,47(3):392-398.
[12]Zelt C A,Smith R B.Seismic traveltime inversion for 2-D crustal velocity structure[J].Geophysical Journal International,1992,108(1):16-34.
[13]刘劲松,刘福田,刘俊,等.地震层析成像LSQR算法的并行化[J].地球物理学报,2006,49(2):540-545.
[14]魏亦文,王彦春.混合插值法重构近地表模型[J].计算机辅助设计与图形学学报,2012,24(4):466-470.
[15]Rickett J,Sava P.Offset and angle domain common image gathers for shot profile migration[R].Stanford Exploration Project,Report 108,2001:1-8.
[16]刘守伟,程玖兵,王华忠,等.偏移距域/角度域共成像点道集与偏移速度的关系[J].地球科学——中国地质大学学报,2007,32(4):575-582.
[17]Liu Z Y.An analytical approach to migration velocity analysis[J].Geophysics,1997,62(4):1238-1249.
[18]Bloor R,Gonzalez A,Alertin U,et al.Tomographic velocity model updating for prestack depth migration[C]//SEG 69th Annual Meeting,Expanded Abstracts,Houston:Society of Exploration Geophysicist,1999:1255-1258.
[19]高亮,李幼铭,陈旭荣,等.地震射线幸几何算法初探[J].地球物理学报,2000,43(3):402-410.
[20]李川,王有学,何晓玲,等.基于二维三次卷积插值算法的辛几何射线追踪[J].地球物理学报,2014,57(4):1235-1240.
[21]韩果花,李川,黄明曦,等.二维复杂速度结构中的射线追踪[J].桂林理工大学学报,2013,33(3):425-429.
[22]McLachlan R I,Atela P.The accuracy of symplectic integrators[J].Nonlinearity,1992,5(2):541-562.

