基于非结构化网格的人工源频率域三维电磁场数值模拟

熊彬，蔡红柱，罗天涯，李长伟，丁彦礼，赵建国

(1.桂林理工大学a.地球科学学院;b.广西矿冶与环境科学实验中心，广西桂林541004;2.College of Mines＆Earth Sciences，University of Utah，Salt Lake City，USA，84112;3.中国石油大学地球物理与信息工程学院，北京102249)

在减少数据解释歧义、降低勘探风险方面，可控源电磁法(CSEM)勘查一直以来都被认为是一种重要的地球物理手段[1-2]。不可否认的是，CSEM勘探方法效果的优劣，将直接取决于人们对野外地质环境电磁响应的深入理解和认识[3]。随着数值技术及计算机性能的快速发展，现在普通的台式工作站已经能容易地处理CSEM三维正演问题。就当前而言，在电磁问题的正演模拟中，应用最为广泛的数值方法就是有限单元法和有限差分法[4]，尽管其他一些方法也伴随着得到了长足的提高和完善，譬如积分方程法[5-7]、有限体积法[8]、对模型电导率施加某些额外约束的近似求解方法[9]、Neumann级数法[10]、人工神经网络法[11]，以及基于低对比度假设的Born-Rytov型近似求解[12]，等等[13]。

完全非结构化三角形网格或四面体网格以Delaunay法或推进波阵面法为基础，采用三角形(四面体)来填充二维或三维空间，它消除了结构化网格中节点的结构性限制，节点和单元的可控性好，能更好地处理边界，适用于模拟不规则计算区域[14]，在刻画复杂地质构造时有明显优势。非结构化网格在其生成过程中采用一定的准则进行优化判断，能生成高质量的网格，很容易控制网格的大小和节点的密度;此外，它采用随机的数据结构也有利于进行网格自适应。一旦在边界上指定网格的分布，边界之间就可以自动生成网格，无需分块或用户的干预，而且不需要在子域之间传递信息。与此同时，有限单元法能实施完全非结构化网格，使其单元边界能与地下非均质体的特有几何形态达到一致，如偏离的钻孔、流体浸入带以及石油测井中经常遇到的倾斜地层，正是这种自然支持非结构化网格的特性，使得在处理具有一定程度几何复杂性问题时，有限单元法成为了普遍性的首选数值方法[4，15]。

用有限单元法求解电磁感应问题，可基于耦合的矢量位、标量位(A，Ψ)，进而通过数值微分得到电磁场各分量，或直接求解电场与磁场矢量(E，H)，两种方案各有优势[3，16-17]，本文将考虑基于位的CSEM三维有限元正演方案。

1 磁矢量位和电标量位所满足的微分方程

在Coulomb规范下，磁矢量位A和电标量位Ψ在求解模型的边界上连续，且A-Ψ方程对称、简单、通用。限于篇幅，下面直接列出基于Coulomb规范(▽·A=0)下磁矢量位A及电标量位Ψ所满足的二阶微分方程[3-4]

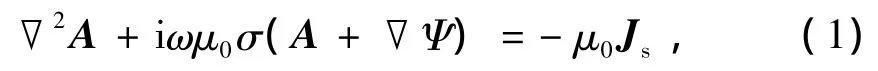
及

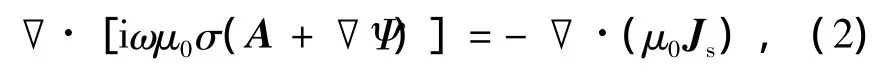
式中:采用正弦谐变型时间因子e-iωt;ω为角频率;μ0为自由空间磁导率;Js为场源电流分布;σ为介质电导率。

为了避免式(1)和(2)中显含场源项带来的奇异性[18]，不妨定义关于电磁场二次位的表达式

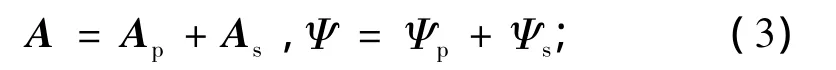
由此不难获得关于电磁场二次矢量位与标量位的控制方程

这里

σp为背景电导率。另外，设定区域边界远离发射场源，以至边界上的电磁场值可以忽略不计;此时，在外边界上施加均匀Dirichlet边界条件[19]

上述方程(4)、(5)和(7)即构成了磁矢量位及电标量位所满足的三维边值问题。

2 有限元分析

2.1 Galerkin线性方程组

很明显，对于均匀全空间介质中的偶极源与回线源，Ψp=0恒成立。在笛卡尔坐标系中，将方程(4)和(5)沿三轴向依次展开

应用Galerkin方法[20]，同时引用普通恒等式和散度定理，并注意到外边界条件，容易得到关于标量函数(Asx、Asy、Asz、Ψs)的体积分方程组

试验函数N(r)可以选择为基于节点的插值函数[20－21]。

2.2 总体系数矩阵的形成

用四面体单元离散整个计算区域，在各个单元中，电导率为常数，磁矢量位As及电标量位Ψs呈线性变化

将上述两式代入方程(12)～(15)，很明显，这里的单元矩阵是一个分块矩阵[4，21]，由4×4个子矩阵Kst(s，t=1，…，4)构成

这里

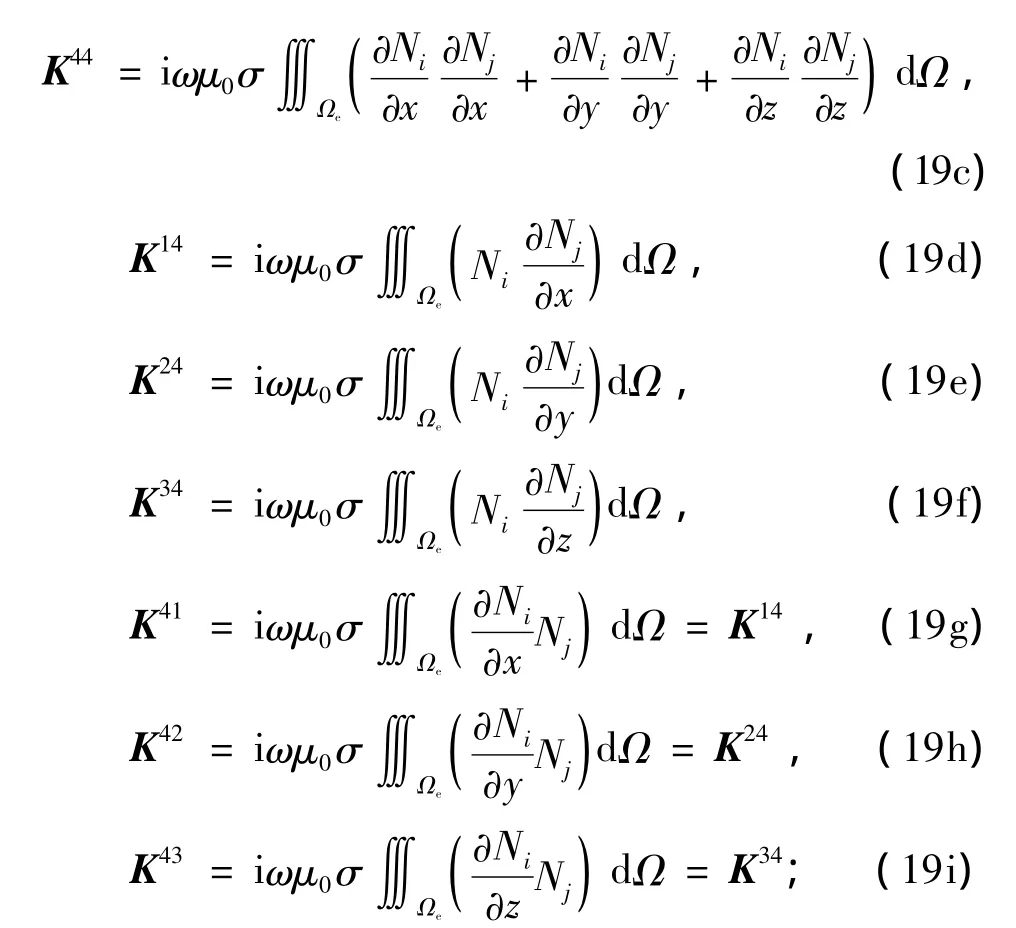
如此逐单元分析，并将单元的系数矩阵扩展成由全体节点组成的系数矩阵，而后，将各个单元系数矩阵中的元加在总体系数矩阵数组中的相应位置，即K=∑，由此，二阶微分方程经由离散最终得到如下线性代数方程组

b为一次位所形成的右端项列向量。

2.3 稀疏线性方程组的求解

方程组(20)中的K是一个大型稀疏对称的非正定矩阵。鉴于目前计算机存贮空间及计算量方面的客观需求，为了求解方程组(20)，即便采用现今最为高效的直接求解方法依然会是一个不小的挑战;再者，为便于算法日后的并行化，文中采用基于复系数Krylov子空间的迭代方法(QMR)进行大型稀疏线性方程组的求解[22]。

这里，diag()即为取总体系数矩阵对角线上的值。

3 均匀介质中的一次位

根据文献[25]，这里直接列出电导率为σ0的均匀介质中一次磁矢量位及电标量位的解析计算式

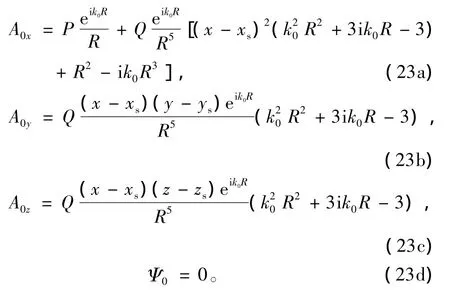
这里

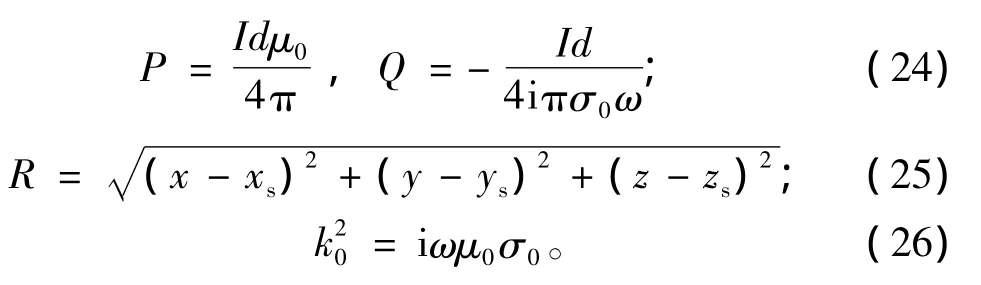
式中:I为供电电流;d为偶极长度;xs、ys、zs为偶极源中心位置坐标。

4 位的导数

上述有限单元法求解得到的是关于电磁场的二次位(As、Ψs)，为了进一步得到物理意义上的电磁场(Es、Hs)各分量，必须借助有效的数值微分方法来获取

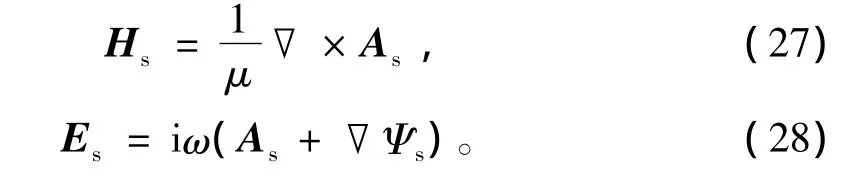
在规则化网格中，常规做法就是在节点周围的单元中，分别计算场的导数，再通过面积加权平均或体积加权平均来获得节点上场的导数[1];或者直接利用节点附近沿某一坐标轴方向若干点上的场值，通过等距差商的办法来获取节点上场的偏微分值[21]。

针对完全非结构化网格上的二次位，则采用滑动最小二乘插值的办法[26-27]来获取所期望节点t处电磁场各二次分量。不失一般性，设单元中场的线性描述

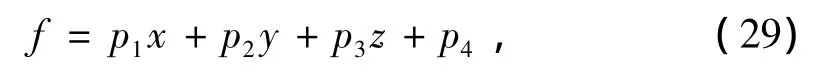
显然，式中的系数pi(i=1，…，4)即为所需的场沿各坐标轴的导数。略去中间推导过程，这里直接列出最终求取系数pi的方程

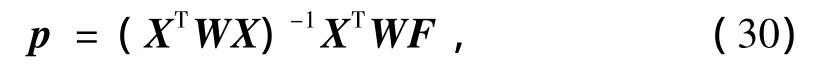
其中:

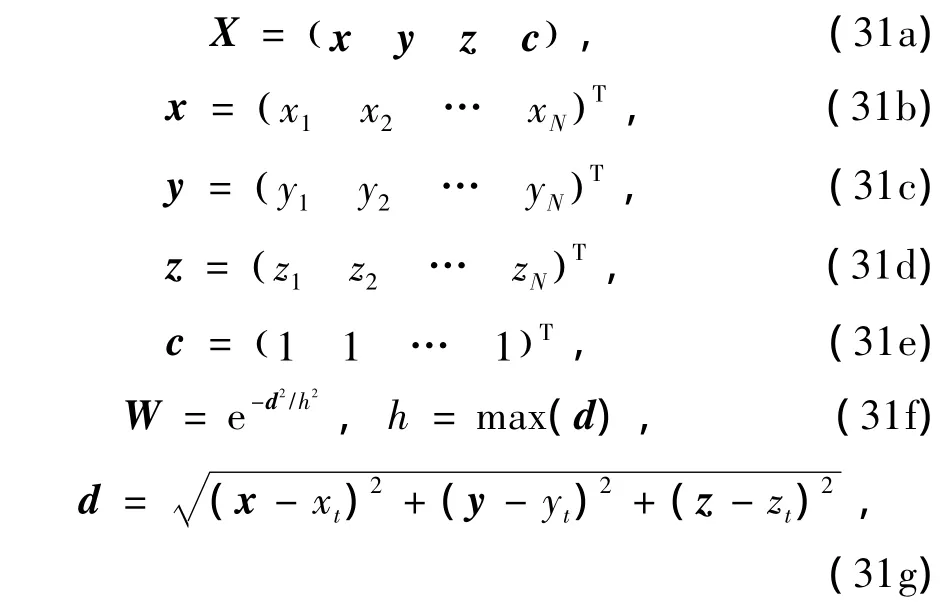
F即为期望节点t附近N个网格节点上的二次位的值。

5 数值算例

为了验证文中所提方案的可靠性和有效性，利用COMSOL Multiphysics生成四面体单元网格，以3例典型地电模型从不同角度进行分析和阐述。具体计算平台参数描述:Dell Precision T7610 CTO Base工作站，双英特尔至强处理器E5-2697 v2(12核HT，2.7GHzTurbo，30 MB)。

5.1 均匀介质中赋存单一目标体

如图1所示，均匀背景电导率为0.1 S/m，沿轴向布设水平电偶极子源，电偶极矩为100 Am，位于z=0界面以上100 m的(0，0，-100)处，发射频率为10 Hz。目标体电导率为0.01 S/m，大小为500 m×500 m×400 m，其几何中心位于(0，0，800)处。

计算区域设置为Ω={-2 000 m≤x，y≤2 000 m;-1 000 m≤z≤2 000 m}，以美国犹他大学电磁法正反演科研组CEMI的积分方程法结果为参照，本文给出了对比结果，详见图2(为充分体现各分量的细节，这里分别考察了二次场的实部和虚部)。结果表明，两者吻合情况令人满意。基于此，图3、图4分别给出了模型Ⅰ中二次电场和二次磁场实、虚部的平面分布。其中，由于受趋肤深度及网格剖分方面的影响，磁场分量Hsx出现一定程度的误差。

图2 有限单元解与积分方程解的对比Fig.2 Comparison of FE solution against IE solution

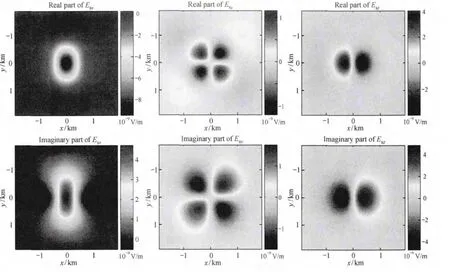
图3 模型Ⅰ二次电场三分量实部与虚部平面图Fig.3 Real and imaginary parts of secondary electric field for ModelⅠ

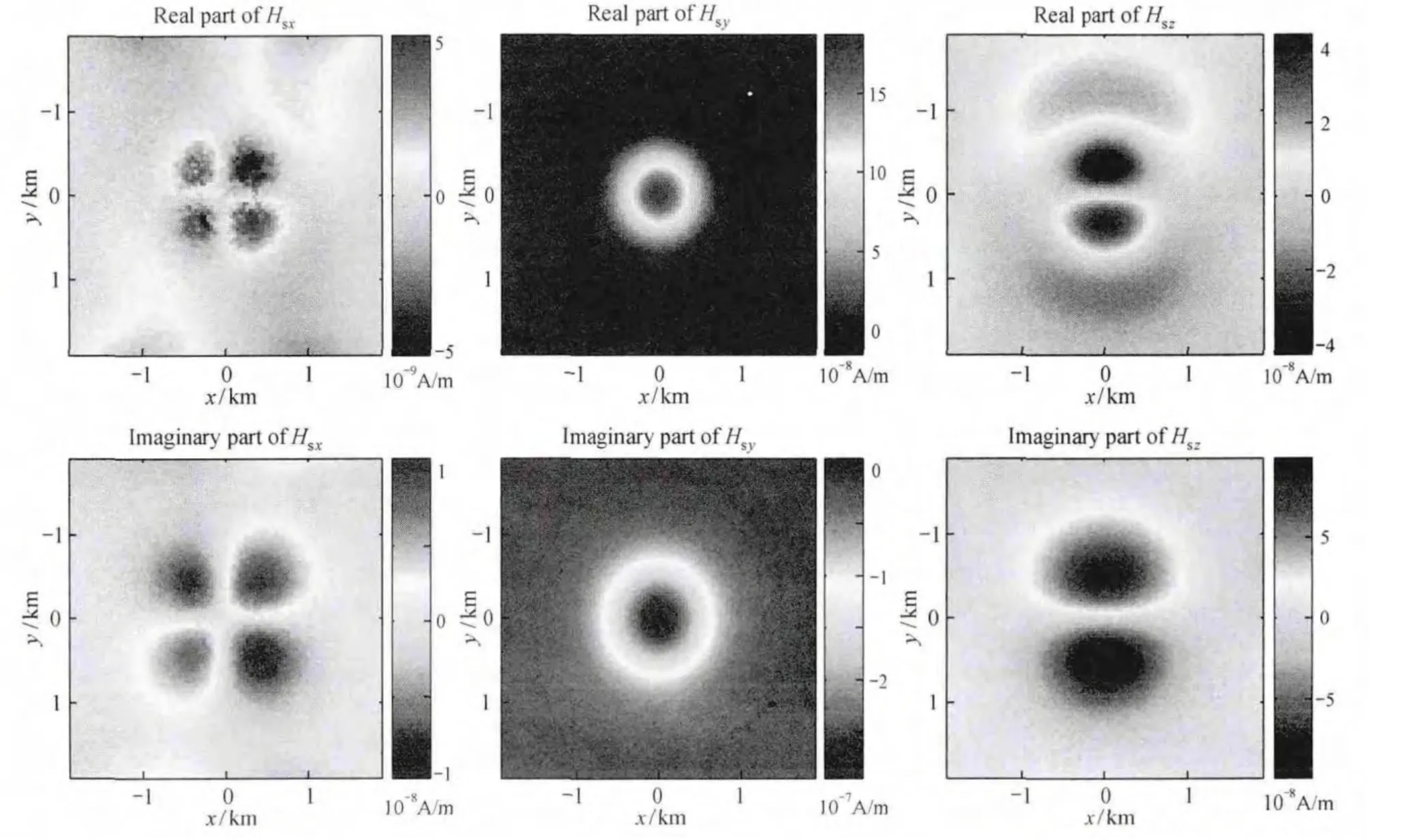
图4 模型Ⅰ二次磁场三分量实部与虚部平面图Fig.4 Real and imaginary parts of secondary magnetic field for ModelⅠ

5.2 多个目标体的电磁响应

图5给出了一均匀背景中赋存有2个矩形异常体的情况，背景电导率值为0.01 S/m，同上，在z=0界面以上100 m的(0，0，100)处，沿轴向布设水平电偶极子源，电偶极矩为100 Am，发射频率为10 Hz。两目标体电导率分别为0.1、0.001 S/m，大小均为400 m×400 m×200 m，其几何中心分别位于(-800，0，1 000)、(800，0，600)处。

计算区域的设置及有限元网格的剖分均同上，仍以二次场各分量的实部和虚部为研究对象，考察各分量的固有特征及变化规律，模型Ⅱ中二次电场和二次磁场实、虚部的平面分布见图6、图7。

图5 模型Ⅱ示意图Fig.5 Map of ModelⅡ

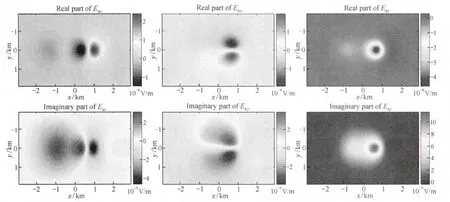
图6 模型Ⅱ二次电场三分量实部与虚部平面图Fig.6 Real and imaginary parts of secondary electric field for ModelⅡ

图7 模型Ⅱ二次磁场三分量实部与虚部平面图Fig.7 Real and imaginary parts of secondary magnetic field for ModelⅡ

5.3 海底地形模型

图8所示为储藏在海丘之下的一块藏油区，最大海水深度1 km，最浅500 m，海水电导率取3.3 S/m，沉积层水平和垂直方向电导率分别为1、0.8 S/m，油藏范围:xy方向-1 000～1 000 m，z方向2 000～2 100 m，油藏区域水平和垂直方向电导率分别为0.05、0.005 S/m，场源位于(-3 000，0，500)m处，沿轴向布设水平电偶极子源，电偶极矩为100 Am，发射频率为1 Hz。

如图9所示，Ex二次场的实部在海丘处显著增大，与5.1节相比较可知，海丘对Ex二次场的实部的影响远大于藏油区的影响。

图8 模型Ⅲ示意图Fig.8 Map of ModelⅢ

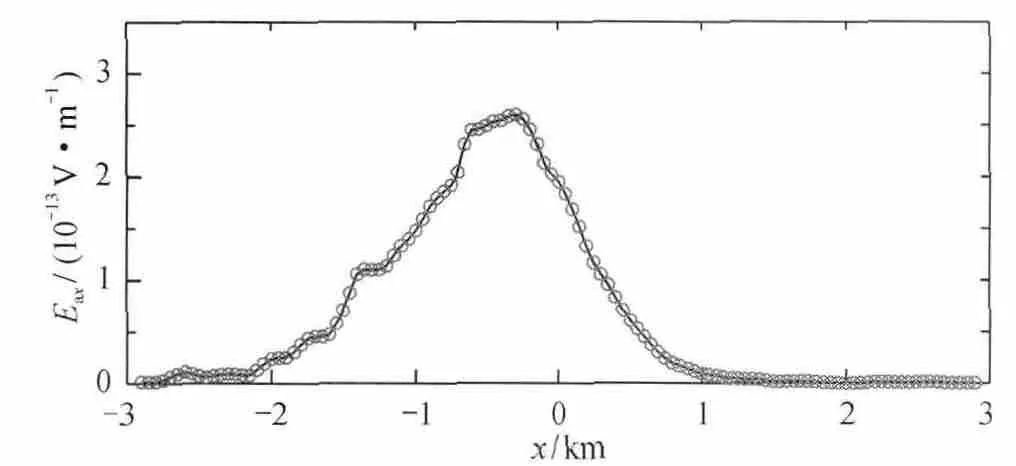
图9 模型Ⅲ二次场的实部Fig.9 Real part of secondary electric field for ModelⅢ

6 结束语

具有良好的通用性，适用于井中电磁、海洋电磁、环境地球物理等非均匀介质中的电磁感应基础研究。在后续研究中，本课题组将在本文所提正演方案的基础上，致力于解决人工源电磁法的三维反演问题。

美国犹他大学电磁法正反演科研组(CEMI)提供了优良的科研环境，审稿人对本文提出了宝贵意见，在此一并致谢。

采用COMSOL生成完全非结构化网格，本文建立了基于磁矢量位、电标量位的人工源频率域电磁法三维正演的流程与算法，通过与国际同行研究结果进行对比，文中正演算法是可靠和有效的。

由于Coulomb规范下磁矢量位、电标量位在求解区域内连续，满足节点型有限元法的最基本假设，避免了直接求解时对场的强制连续性要求。采用非结构化网格进行区域剖分，一方面可以在不影响解的精度的前提下，它能使得单元诸多属性参数达到最大程度的优化;另一方面，也是其不足之处，它会降低方程求解的收敛速度，针对这一问题，文中采用预条件因子改善稀疏矩阵条件数，大大提高了方程组求解收敛效率。本文算法具有良好的移植性，对方程组右端项稍加修改，即可适用于磁性源CSEM的三维正演。该方法也

[1]Nabighian M N.Electromagnetic Methods in Applied Geophysics—Theory(Volume 1)[M].Tulsa:Soc.Expl.Geophys.，1988.

[2]Nabighian M N.Electromagnetic Methods in Applied Geophysics:Volume 2，Application，Parts A and B[M].Tulsa:Soc.Expl.Geophys.，1991.

[3]Badea E A，Everett M E，Newman G A，et al.Finite-element analysis of controlled-source electromagnetic induction using Coulomb-gauged potentials[J].Geophysics，2001，66(3):786-799.

[4]Puzyrev V，Koldan J，de la Puente J，et al.A parallel finiteelement method for three-dimensional controlled-source electromagnetic forward modelling[J].Geophysical Journal International，2013，193(2):678-693.

[5]Zhdanov M S，Fang S.Quasi-linear series in three dimensional electromagnetic modeling[J].Radio Science，1997，32(6):2167-2188.

[6]Zhdanov M S.Geophysical Electromagnetic Theory and Methods[M].Oxford:Elsevier，2009.

[7]何展翔，王志刚，孟翠贤，等.基于三维模拟的海洋CSEM资料处理[J].地球物理学报，2009，52(8):2165-2173.

[8]Weiss C J，Constable S.Mapping thin resistors and hydrocarbons with marine EM methods，Part II—Modeling and analysis in 3D[J].Geophysics，2006，71(6):G321-G332.

[9]McKirdy D McA，Weaver J T，Dawson T W.Induction in a thin sheet of variable conductance at the surface of a stratified earth-II.Three-dimensional theory[J].Geophysical Journal International，1985，80(1):177-194.

[10]Avdeev D B，Kuvshinov A V，Pankratov O V，et al.Highperformance three-dimensional electromagnetic modelling using modified Neumann series.Wide band numerical solution and examples[J].Journal of Geomagnetism and Geoelectricity，1997，49:1519-1539.

[11]Spichak V，Popova I.Artificial neural network inversion of magnetotelluric data in terms of three-dimensional earth macroparameters[J].Geophys.J.Int.，2000，142:15-26.

[12]Song L P，Liu Q H.Fast three-dimensional electromagnetic nonlinear inversion in layered media with a novel scattering approximation[J].Inv.Prob.，2004，20(6):S171-S194.

[13]Avdeev D B.Three-dimensional electromagnetic modelling and inversion from theory to application[J].Surveys in Geophysics，2005，26:767-799.

[14]陈炎，曹树良，梁开洪，等.结合前沿推进的Delaunay三角化网格生成及应用[J].计算物理，2009，26(4):527-533.

[15]雷林林，刘四新，傅磊，等.海洋电磁法勘探油气的三维正演模拟[J].世界地质，2012，31(4):797-802.

[16]徐志锋，吴小平.可控源电磁三维频率域有限元模拟[J].地球物理学报，2010，53(8):1931-1939.

[17]汤井田，任政勇，化希瑞.Coulomb规范下地电磁场的自适应有限元模拟的理论分析[J].地球物理学报，2007，50(5):1584-1594.

[18]林昌洪，谭捍东，舒晴，等.可控源音频大地电磁三维共轭梯度反演研究[J].地球物理学报，2012，55(11):3829-3839.

[19]Bгró O，Preis K.On the use of the magnetic vector potential in the finite element analysis of three-dimensional eddy currents[J].IEEE Trans.Magn.，1989，25(4):3145-3159.

[20]Jin J M.Finite Element Method in Electromagnetics[M].2nd ed.New York:John Wiley＆Sons，2002.

[21]徐世浙.地球物理中的有限单元法[M].北京:科学出版社，1994.

[22]Saad Y.Iterative Methods for Sparse Linear Systems[M].2nd Edition.Philadelphia:Society for Industrial and Applied Mathematics，2003.

[23]吴建平，王正华李晓梅.稀疏线性方程组的高效求解与并行计算[M].长沙:湖南科学技术出版社，2004.

[24]Ascher U M，Chen Greif.A First Course in Numerical Methods[M].Philadelphia:Society for Industrial＆Applied Mathematics，2011.

[25]Liu C S，Everett M E，Lin J，et al.Modeling of seafloor exploration using electric source frequency domain CSEM and the analysis of water depth effect[J].Chinese J.Geophys.，2010，53(4):669-683.

[26]Tabbara M，Blacker T，Belytschko T.Finite element derivative recovery by moving least square interpolants[J].Comp.Meth.Appl.Mech.Eng.，1994，117:211-223.

[27]Alexa M，Behr J，Cohen-Or D，et al.Computing and rendering point set surfaces[J].IEEE Trans.Vis.Comput.Graphics，2003，9(1):3-15.

[28]Schwarzbach C，Börner R-U，Spitzer K.Three-dimensional adaptive higher order finite element simulation for geo-electromagnetics—A marine CSEM example[J].Geophysical Journal International，2011，187:63-74.