共轭梁比拟方法及在变截面梁计算中的应用

王赞芝，王晓，余佳代，邓年春，马瑞彦，江林雁，王淼，刘娥珍

(1.广西科技大学土木建筑工程学院，广西柳州545006;2.广西大学土木建筑工程学院，南宁530004;3.河北工程技术学院，石家庄050091;4.中煤邯郸设计工程有限责任公司，河北邯郸056031;5.柳州铁道职业技术学院，广西柳州545616;6.广西科技师范学院，广西来宾546199)

变换法与比拟法是常用的解决数学物理问题的方法。变换法中最简单、最熟知的方法是对数的运用，它可将数的乘除运算变换为加减运算，从而减轻了计算工作量。之后出现的复变函数的保角变换方法、微积分方程的Fourier变换、Laplace变换、Hankel变换解法等，都能够将原来不能解决的问题变得可解，原来处理起来很复杂的问题处理起来比较简单。比拟法常见的有水电比拟(将液体的流体力学问题用电磁学方法解决)、气液比拟(将液体的力学问题用气体实验方法解决)[1]、塑性力学扭转比拟(将理想塑性材料的等截面直杆扭转问题用沙堆比拟)[2]。本文介绍的是梁(真实的梁)与它的共轭梁(虚拟的梁)的比拟。共轭，本意指按一定的规律相配的一对，有对称的含义，如共轭复数，它们关于x轴对称。可以看出，通过共轭梁这种比拟，能将求实体梁挠度的问题转化为求虚拟梁的弯矩问题。在此基础上将连续分布的虚荷载，按照静力等效的原则，转换成集中作用的虚荷载，这样，计算虚梁的内力就变得简单并且可以程式化，在计算复杂的变截面梁时该方法具有一定的优越性。

1 共轭梁比拟方法

1.1 实梁与虚梁微分方程的对应关系

一般情况下，梁弯曲的微分方程为[3]

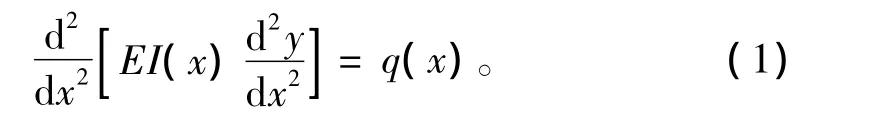
当I(x)不是常数时，方程(1)是变系数四阶常微分方程，因此只有特殊情况才能求出解析解[4]，一般采用近似的数值解法[5－8]。

对于变截面梁，尽管方程(1)是变系数的，但弯矩、剪力和荷载集度之间仍存在如下的关系:

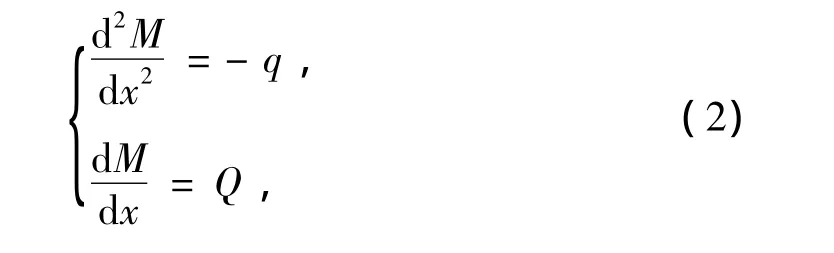
另一方面，梁的变形和内力之间的关系为

比较式(2)与式(3)，单纯从数学的形式上看，两组微分方程是完全相似的，因而求解的步骤和方法也完全相同。于是可以设想，如果将原来实际梁上所产生的当作荷载集度，并用q*表示之:

将它作用到某个虚设梁上，那么，根据式(2)可得

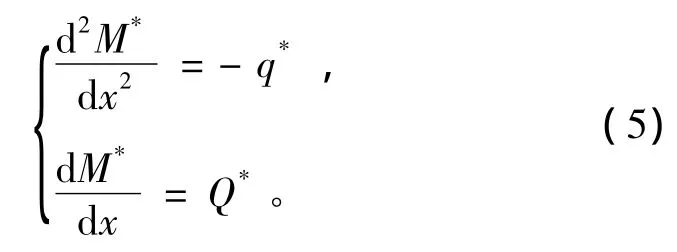
式中的M*、Q*是虚梁的虚弯矩和虚剪力。比较式(3)和式(5)可以看出，虚梁上的虚弯矩和虚剪力分别就是实梁上的挠度和转角。通过这种比拟手段，计算真实梁的挠度和转角可以转化为计算虚梁的弯矩和剪力，这就是共轭梁比拟方法，并将虚梁称为真实梁的共轭梁。

1.2 实梁与虚梁边界条件的对应关系

实梁的边界，一般有固定端、自由端、铰支端、中间铰支座、中间铰、弹性支座[3]等几种情况，分别给出这些实梁的边界条件所对应的虚梁的边界条件。

①固定端

由式(2)、式(3)的对比可以看出，实梁固定端的yA=0对应虚梁=0，实梁的θA=0对应虚梁的=0，因此实梁的固定端对应虚梁的自由端，如图1所示。

图1 实梁的固定端对应虚梁的自由端Fig.1 Fixed end of real beam and counterpart free end of virtual beam

②自由端

按与上述相似的理由，实梁的yA≠0和θA≠0对应于虚梁的≠0和≠0，因此实梁的自由端对应于虚梁的固定端，如图2所示。

图2 实梁的自由端对应虚梁的固定端Fig.2 Free end of real beam and counterpart fixed end of virtual beam

③铰支端

可以容易地看出，实梁的铰支端对应于虚梁的铰支端，这使得运用共轭梁法分析简支梁时不需要对边界条件进行转换，从而带来一定的便利，如图3所示。

图3 实梁的铰支座对应虚梁的铰支座Fig.3 Joint end of real beam and counterpart joint end of virtual beam

④中间铰支座

在中间铰支座A处，yA=0，θA≠0，θA左=θA右;对应的虚梁的条件是=0≠0，QA左=QA右。这样，实梁的中间铰支座对应在A点挠度不受约束的“中间铰”，如图4所示。

图4 实梁的中间铰支座对应虚梁的中间铰Fig.4 Intermediate joint support of real beam and counterpart intermediate joint of virtual beam

⑤中间铰(没有支座)

对于中间铰，实梁的yA左=yA右和θA左≠θA右，对应虚梁的，所以实梁的中间铰对应虚梁的“中间铰支座”，如图5所示。

图5 实梁的中间铰对应虚梁的中间铰支座Fig.5 Intermediate joint of real beam and counterpart intermediate joint support of virtual beam

从以上分析可以看到，在分析实梁的自由端时，并没有利用实梁的MA=0，QA=0;在分析中间铰时，也没有利用实梁的MA=0，QA=0和QA左≠QA右。这是因为在运用共轭梁法求解实梁问题时强调的是用求虚梁内力的方法来求实梁的位移，因此在此都是将实梁的位移边界条件转化为虚梁的力的边界条件。

1.3 运用共轭梁方法的算例

求解图6a所示变截面简支梁在均布荷载作用下的挠度[9]，分为如下几个步骤:

①作实梁的剪力图(图6b)、弯矩图(图6c);

②在各截面将实梁弯矩除以实梁的抗弯刚度，如图6d，这也就是虚梁的虚荷载分布图，是虚梁的外力图;

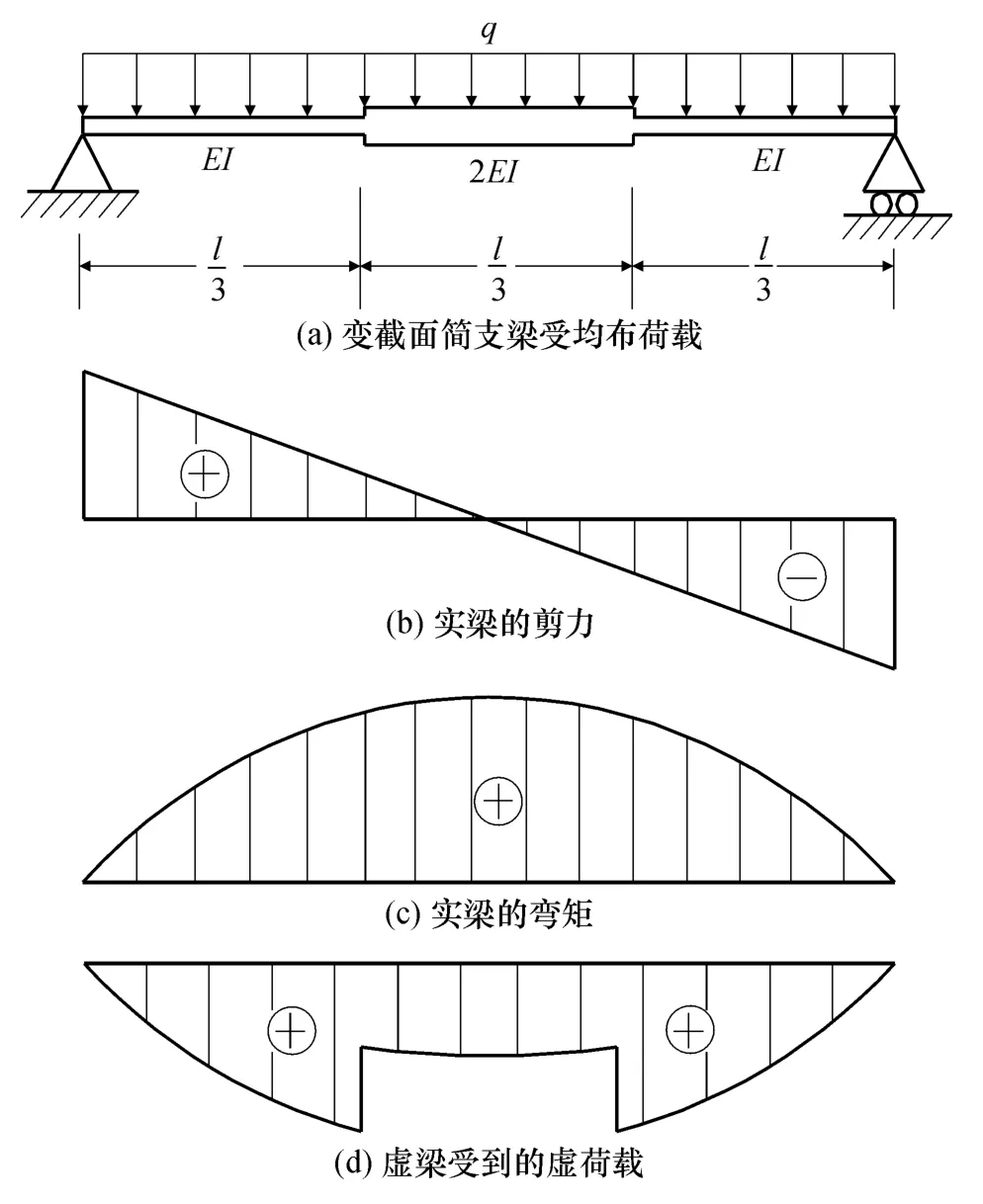
图6 共轭梁法示例Fig.6 Example for conjugate beam method

③根据上面对实梁和虚梁边界条件对应关系的讨论，实梁两端简支，对应的虚梁也是两端简支，这样图6d中的虚梁也是简支梁;

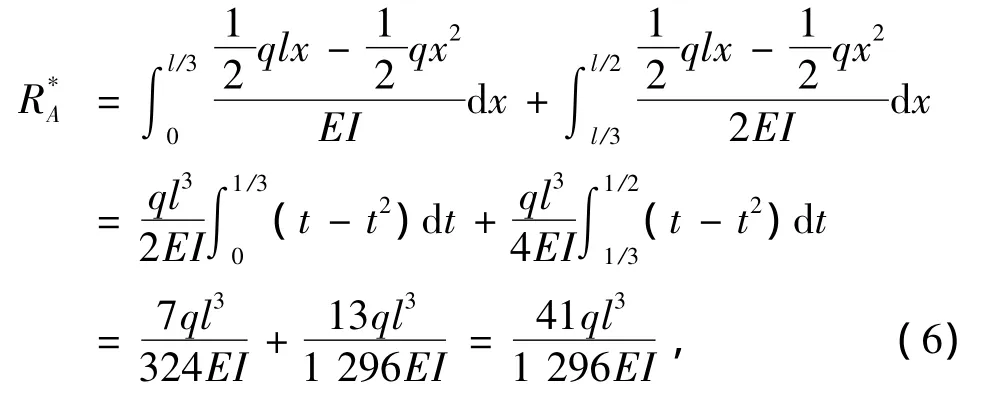
⑤计算虚梁跨中虚弯矩

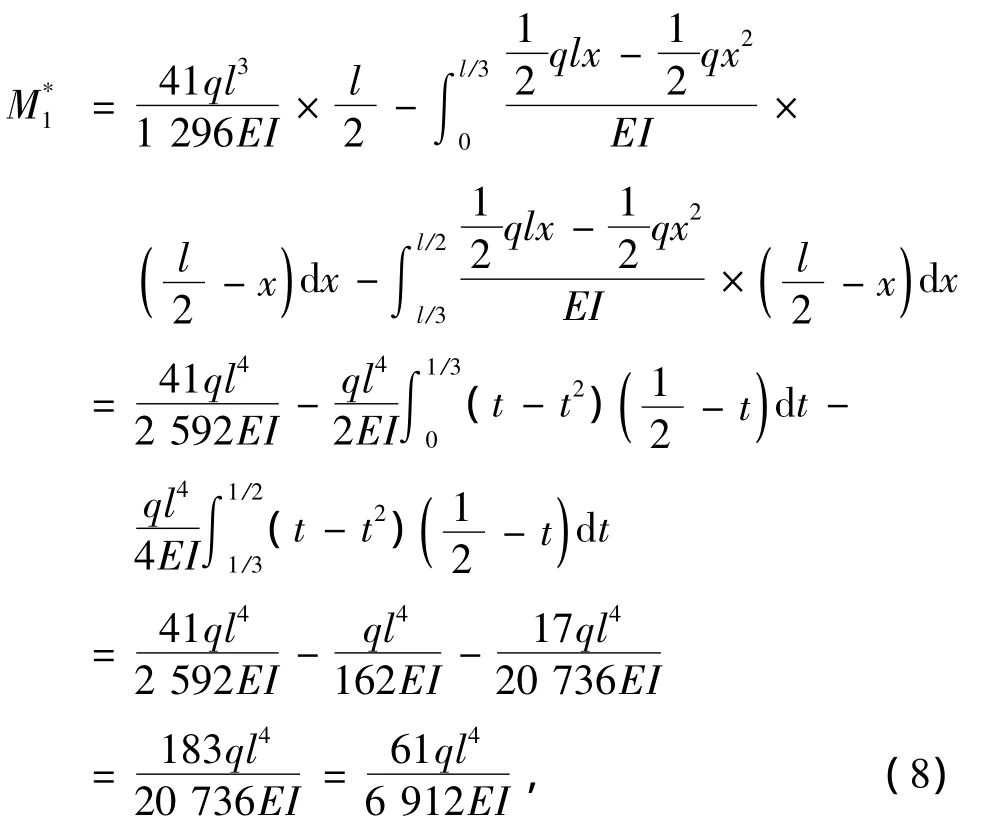
虚梁的虚弯矩M*对应实梁的挠度，因而实梁跨中挠度

1.4 共轭梁法解变截面梁问题的步骤

由算例可以看出，使用共轭梁法计算梁的变形问题包括如下一些步骤:①根据实梁所受外力，画出实梁的剪力图、弯矩图;②将实梁各截面的弯矩除以相应位置处该梁的刚度，得到虚梁的虚荷载;③根据上文实梁与虚梁边界条件的对应关系，确定虚梁的边界条件;④计算出虚梁的支座反力;⑤计算出虚梁的虚剪力、虚弯矩。

虚梁在端部的虚剪力就是实梁在端部的转角，虚梁在跨中的虚弯矩就是实梁在跨中的挠度。

2 共轭梁法的应用

2.1 共轭梁方法的本质

在差分法中，虽然可以处理变截面梁与阶梯轴等，但差分法处理阶梯轴是近似的，因为如果将差分法的节点正好放在截面的突变处，则无法决定在节点处到底取梁左侧的刚度还是取右侧的刚度，因此即使可以通过增加分段个数来提高差分法的精度，用差分法处理变截面梁本身仍然是近似的。

共轭梁法在实质上与直接求解方程(1)是一样的。直接求解方程(1)时，先积分方程(1)两次，得到方程

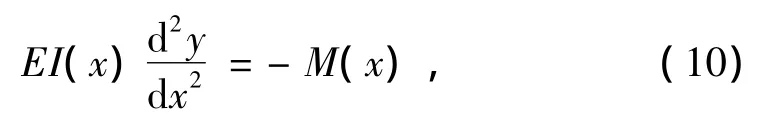
将上式变形为式(3)的第1式，再对式(3)的第1式积分两次，即得梁的挠度表达式y(x)。而在共轭梁法中，也是先求出M(x)，然后形式上把当成虚荷载q*(x)，再对q*(x)积分两次。

也正因为共轭梁法本身是精确的，使得共轭梁法没有简化计算过程，因此也没有减少计算工作量。有时尽管q(x)很简单，但q*(x)也很复杂，所以采用共轭梁方法本身只是转变了解题观念，其本身并不能给计算带来方便。

2.2 等效集中虚荷载

共轭梁法本身没有给计算带来便利，主要是因为虚荷载q*(x)较复杂，直接对q*(x)进行两次积分的工作量很大，要是进行实际工程中处理大型复杂结构的计算，将显得复杂而凌乱。如果能按一定的原则，将q*(x)等效为集中力，则可免除复杂的积分计算，从而显著减少计算工作量，提高计算效率。

按照这一思路对共轭梁法进行改进:q*(x)一般呈曲线分布，将梁分为n个节段、n+1个节点，每个节段长度分别为λ1、λ2、…、λn，将连续分布于全梁的虚荷载q*(x)转换成仅存在于节点的集中荷载，有些类似于有限元方法中对节间荷载的处理，也类似于桁架结构设计时对桁架节间荷载的处理[10]。

如图7所示，设分布虚荷载q*(x)在节点A、B、C三点上的值分别为a、b、c，则在两个相邻节间的q*(x)可用下列二次插值函数q2(x)来拟合:

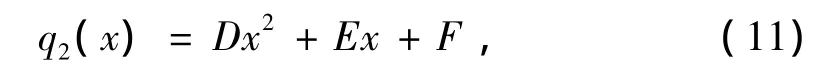
将x=0、x=λ1、x=λ1+λ2及相应的函数值a、b、c分别代入式(11)，以计算出式中的常数D、E、F，得到拟合后的q2(x):

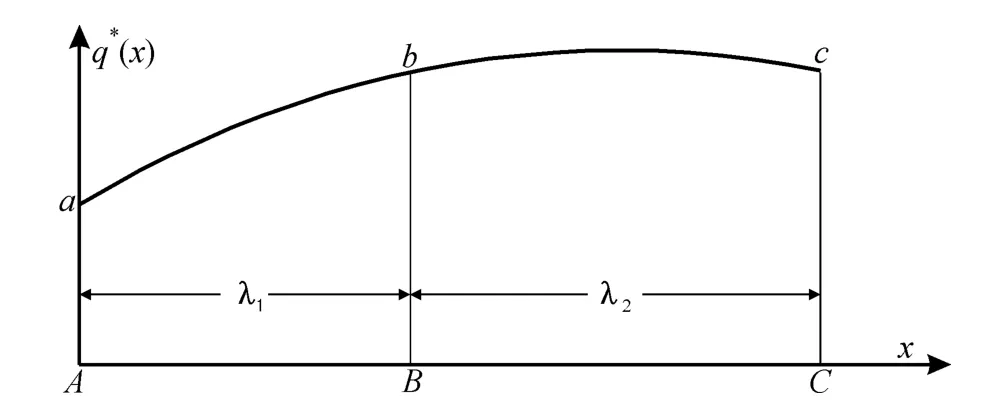
图7 等效集中荷载Fig.7 Equivalent accumulative loads

如果采用等间距划分节段，则λ1=λ2=…=λn=λ，式(12)将得到简化;如果虚荷载q*(x)在某节间呈线性分布或在全梁呈折线分布，则只需在这些节间线性插值，式(12)也得到简化。

设两节段AB及BC上的分布荷载等效到A、B、C三点的集中虚荷载分别为，现取出其中一个节间AB进行分析，于是有

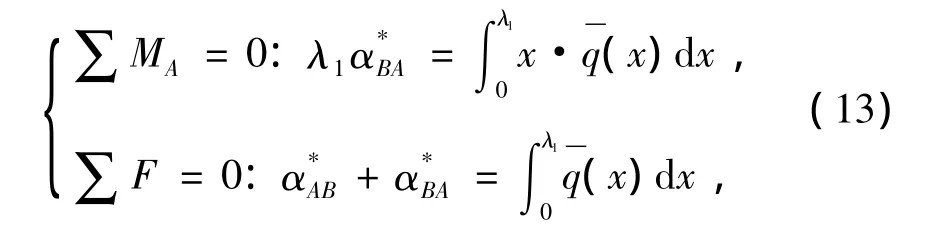
将式(12)代入式(13)，整理后可以解得

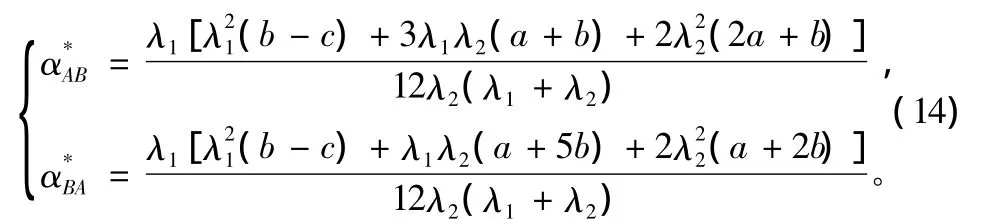
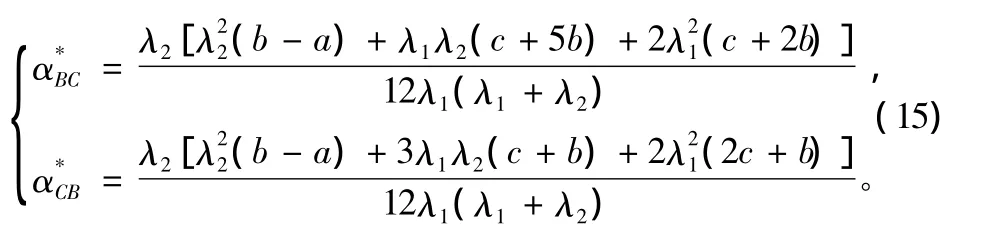
2.3 改进后的共轭梁方法

图8a为一变刚度简支梁，根据外荷载所得的剪力图如图8b所示，弯矩图如图8c所示，图8d是按照式(4)计算得到的作用于虚梁上的分布虚荷载q*(x)。将梁沿纵向划分为n段，每段长度分别为λ1、λ2、…、λn。显然，梁段划分愈细，计算精度愈高，但计算工作量却要大一些。根据分布虚荷载q*(x)计算出的等效集中虚荷载(图8e)，同时标出由其计算出的虚梁的两个虚支反力A*、B*，再根据图8e画出虚梁的虚剪力图8f、虚弯矩图8g。

按照“合乎情理和方便使用”的原则，可以自然地规定下列物理量的正、负号。

图8 改进的共轭梁方法计算步骤Fig.8 Calculating procedure for improved conjugate beam method

①荷载:凡荷载作用方向朝上者为正，这样图8a中两个支座反力A、B为正，外力P为负;

②剪力:凡使截面左边合力向上者为正，这样图8b中集中力左侧的剪力为正;

③弯矩:凡使顶部纤维受压者为正，这样图8c中的弯矩为正;

⑤坡度(或斜率):实梁挠曲线的坡度φi是虚梁的虚剪力V*，正的坡度相应于实梁的挠度从左到右增加，图8f中左半部分的坡度为正;

⑥挠度:实梁的挠度yi是虚梁的虚弯矩M*，向下的挠度yi为正挠度，与实梁正的弯矩相对应。

2.4 算例

已知条件见图9a，试求梁的挠度与端转角。本例将梁全长等分为6段。

①按图9a计算出梁的弯矩(图9b)。

④把此虚梁当成普通的简支梁，按式(13)同样的原理，根据图9d计算出虚梁两端支点处的支反力A*和B*，得这两个值也一并标在图中。

⑤用与画传统的剪力图同样的方法，画出图9d所示虚梁的虚剪力图(图9e)。

⑥根据图9e的虚剪力图，画出虚弯矩图(图9f)。

图9 改进后的共轭梁法算例Fig.9 Example for improved conjugate beam method

这个虚梁的虚弯矩M*，就是实梁的挠度y。因此此梁在节点2#有最大挠度(单位)。

值得说明的是，在图8e和图9d的虚外力图中，故意将虚支反力A*画得向左偏离一些，将支反力B*向右偏离一些。这样在图9e中，表示的是梁在端点A的切线的斜率，而1 115表示的是梁在A－1#这一段的平均斜率。端点B的情况与此类似。这是因为，是将原来分布在A－1#节间的分布荷载等效而来的，实际上在这个虚梁的A端并无这一集中虚荷载。也就是说，在图9f中，A－1#间的挠曲线本来不是直线，而是曲线。对于曲线，在A点切线斜率当然不同于在A－1#段的切线斜率。

3 结束语

本文从方程(2)和方程(3)具有相似性出发，提出共轭梁的概念，导出实梁的各种边界条件所对应的虚梁的边界条件。总结了共轭梁法的本质，在此基础上，对其作了改进，发展为计算变截面梁挠度的改进的共轭梁方法。计算时，将变截面梁分为若干节段，把实梁的当作共轭虚梁的虚荷载q*，作用在虚梁上的节间虚荷载拟合为二次抛物线分布，按静力等效的原则将抛物线分布的虚荷载q*转换成若干个作用于虚梁结点上的等效集中虚荷载，然后计算虚集中力作用下虚梁各个截面处的虚剪力、虚弯矩。依据实梁与虚梁的对应关系，虚剪力与虚弯矩就是实梁的截面转角和挠度，由此得到原来实梁问题的解答。

[1]许维德.流体力学[M].北京:国防工业出版社，1979:112－207.

[2]Hendry A W.Elements of Experimental Stress Analysis[M].Oxford:Pergamon Press，1977:58－61.

[3]陈铁云，陈伯真.船舶结构力学[M].北京:国防工业出版社，1984:14－17.

[4]宋启根，徐梁，宋丹.变截面梁柱刚度方程的Bessel函数解[J].计算力学学报，2001，18(3):355－357.

[5]秦荣，王涛，王晓峰.压电智能梁力电耦合应力应变分析的智能样条有限点法[J].桂林工学院学报，2007，27(3):343－347.

[6]王赞芝，江林雁，江培信.变截面连续梁抗扭惯矩修正系数的计算方法[J].铁道标准设计，2011(4):45－49.

[7]王赞芝，胡如成，张鹏，等.多跨连续梁弯曲自由振动的波动解法[J].四川建筑科学研究，2010，36(2):35－37.

[8]刘鸿文.材料力学Ⅱ[M].5版.北京:高等教育出版社，2011:261.

[9]王国周.钢结构——原理与设计[M].清华大学出版社，1993:353.

[10]程翔云.梁桥理论与计算[M].北京:人民交通出版社，1990:406－550.

[11]李国豪.桥梁结构稳定与振动[M].北京:中国铁道出版社，1992:87－89.

[12]朵英贤.工程中的纵向振动[M].北京:国防工业出版社，1983:237－239.

[13]Barber J R.Intermediate Mechanics of Materials[M].New York:McGraw-Hill Companies，Inc.，2001:339.