数控转塔冲床横梁结构多目标拓扑优化设计*

罗 黎 孙蓓蓓 周易达

(东南大学机械工程学院，江苏 南京 211189)

数控转塔冲床是一种加工多孔薄板的冲裁设备，横梁是数控转塔冲床的送料机构，其刚度与模态频率对冲床的稳定性、加工精度等性能影响显著。随着数控转塔冲床工作速度的提高，横梁的静动态特性尤为重要，而结构优化是提高横梁静动态特性最有效的途径之一。

拓扑优化技术是目前机床企业广泛应用的一种结构优化方法，相较于尺寸优化和形状优化，拓扑优化［1-2］具有更多的设计自由度和更大的设计空间，可以在均匀分布材料的设计空间内找到最佳分布方案，缩短结构改进设计周期，提高机床性能。

目前，国内外拓扑优化设计主要集中在采用传统的单目标的拓扑优化问题上，例如以刚度最大化为目标函数的单目标拓扑优化问题［3-4］，或是以频率最大化为目标函数的拓扑优化设计［5］，然后再对新的拓扑结构进行模态分析、静力分析等，这样可能会出现结构刚度和频率之间的不一致性和不可协调性，因而很难得到最优拓扑结构。

为避免传统的单目标优化设计方法无法同时考虑多个优化目标的缺点，本文以数控转塔冲床横梁为对象，采用多目标拓扑优化的方法进行结构优化设计。首先建立横梁准确的有限元模型，基于加权欧氏距离法，建立横梁多目标拓扑优化的目标函数，应用变密度法进行多目标拓扑优化计算，并根据拓扑优化结果对横梁进行结构改进设计，在保持横梁质量不变前提下，提高刚度与固有频率。

1 加权欧氏距离法

任何一个目标函数的目标值都可以转化为最小值问题，因此所有的多目标函数都可以表示为:

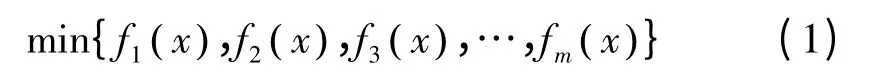
式中:m≥2，f1(x)，f2(x)，f3(x)，…，fm(x)分别为每个单目标函数，优化的目的是使全部单目标函数同时最小化。单目标优化问题往往只存在一个最优值，而多目标优化至少有两个或两个以上的目标函数，其解通常是一组Pareto 解。假设一个多目标问题，y1、y2、…、ym分别为每一个单目标函数的最优解，记为y=(y1，y2，…，ym)，x1、x2、…、xm为多目标问题的Pareto 解，记为x=(x1，x2，…，xm)，那么多目标优化问题的Pareto解即为与最优解距离最小的矢量，因此该多目标优化问题可以简化为单目标的优化问题，可以表示为:

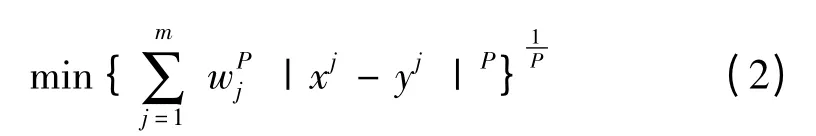
式中:P≥1;wj为每个目标函数的权重，=1，wj＞0。

P 取值不同时，目标函数意义具有不同的意义，当P=2 时，目标函数表示Pareto 解与最优解向量之间的最小化加权欧氏距离，故本文取P=2 建立拓扑优化的目标函数，由于每个目标函数的单位、量度不一样，因此需要将目标函数的Pareto 解与其最优解的距离相对化，将目标函数无量纲化，所以式(2)中的目标函数可以转化为下面的单目标函数优化问题:

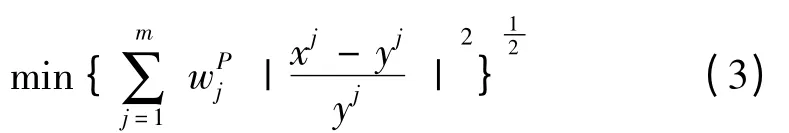
2 多目标拓扑优化目标函数

2.1 静态多刚度拓扑优化模型

静态优化设计的目标为结构刚度最大化，对结构刚度最大化拓扑优化是研究在设计域内得到使结构刚度最大的材料分布形式的问题。横梁在不同的工况下具有不同的静态特性，多工况下的刚度拓扑优化问题通常称为多刚度拓扑优化问题。横梁在每一个工况下对应着一个刚度的最优拓扑结构，所以不同的工况将得到不同的拓扑结构。因此，多刚度拓扑优化问题实际上是属于多目标拓扑优化问题。

在处理该类问题时，通常把刚度最大问题等效为柔度最小问题来研究，由加权欧氏距离法可以得到拓扑优化的目标函数为:

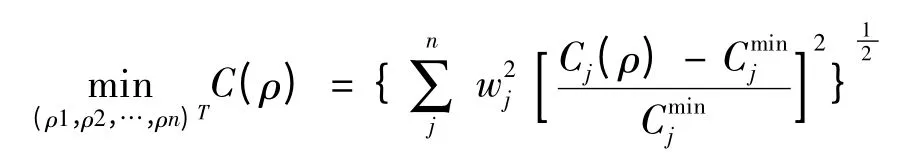
式中:n 为载荷工况总数;wj为第j 个工况的权值;Cj(ρ)为第j 个工况的柔度目标函数;Cminj 分别为第j 个工况柔度目标函数的最小值。

2.2 模态频率拓扑优化模型

结构在振动时，低阶模态反映结构的动态特性，而高阶模态对结构影响较小，因此动态拓扑优化设计时将低阶的几阶模态频率最大化作为目标函数，以结构体积做为设计约束。但是在优化过程中经常会遇到这样的情况:当其中一个阶次的频率达到最大时，其他阶次频率可能降到一个较低的值，而且几阶频率之间可能会相互调换次序。这样就会出现目标函数振荡问题。为了避免几阶频率目标函数出现振荡的现象，此处采用上述方式定义模态频率拓扑优化的目标函数:

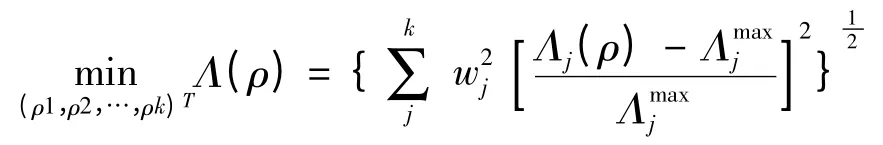
式中:n 为载荷工况总数;wj为第j 阶模态频率的权重值;Λj(ρ)为第j 阶模态频率目标函数为第j 阶模态频率的最大值。

该方法定义了一个光滑的目标函数。在优化过程中，当公式中的几个低阶模态的频率发生交替时，目标函数仍然保持光滑，这是因为这几个低阶模态的贡献在公式中已经被考虑了。

2.3 同时考虑静动态性能的多目标拓扑优化目标函数

结构多目标拓扑优化是以体积分数作为设计约束，同时考虑静态多刚度和振动频率目标的优化设计，优化目标函数可以表示为:

式中:F(ρ)表示优化目标函数;w 为柔度系数权重。

3 横梁结构多目标拓扑优化

3.1 有限元模型的建立与验证

如图1 所示，数控转塔冲床横梁主要由滚珠丝杠传动系统、3 根并联方管、轴溜板、电动机、护罩、底下支架等组成，横梁通过电动机带动滚珠丝杠实现加工板材沿X、Y 方向进给运动。

横梁属于大型复杂装配件结构，在建立有限元模型时应考虑各部件间的连接方式。机床上比较典型的连接方式有焊接、附加质量、滚动导轨结合面、刚性连接等，本文所研究的对象各部件间的连接方式在hyperworks 软件中分别通过CWELD 单元、CONM2 单元、CELAS1 弹簧单元、RBE2 单元来实现，横梁各部件连接方式如表1 所示。

表1 横梁各部件间连接方式

利用CAD 软件Solidworks 对几何模型进行简化处理:忽略工艺上的倒角和倒圆以及连接用的小直径孔;由于拓扑优化设计需要消耗大量的计算空间与时间，并且机床横梁整体结构较大，为了提高有限元模型的计算精度，节省计算时间与空间，将实体结构划分为六面体网格，薄板结构划分为四边形面网格;在hypermesh 中对零部件进行网格划分，并建立相应的连接关系;横梁主要通过Y 方向导轨固定在机身上，约束其底部六个方向的自由度。最终建立的有限元模型如图2 所示，网格总数为274042，计算X 轴溜板位于中间时横梁的约束模态;模态实验采用单点激励多点响应的方法，锤击激励频率范围为0～1000 Hz。表2 所示为横梁模态测试与有限元计算结果对比，固有频率最大误差为6.8%，在误差允许范围内，前四阶振型如图3 所示(模态实验的第二阶振型未激励出来)，可以看出实验模态振型与有限元计算的模态振型一致，因此验证了本文所建有限元模型的正确性。

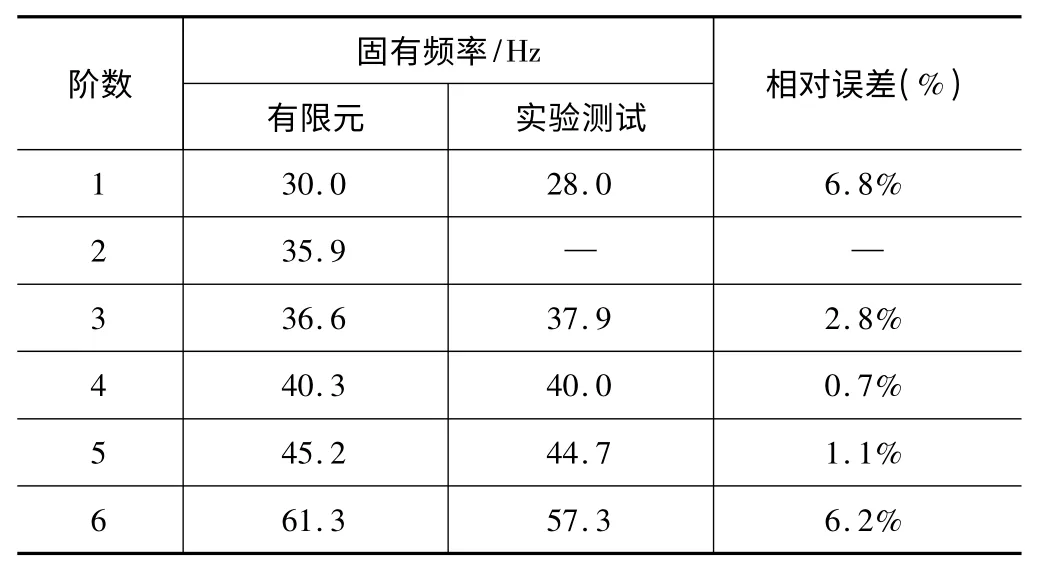
表2 横梁模态测试与有限元计算结果对比

3.2 拓扑优化结果分析

由于X 轴溜板在左右运动过程中，对横梁的动态性能影响较大，尤其是在两个极限位置(最左侧与最右侧)，对横梁的动态性能影响最大。现选取X 轴溜板位于最左侧时进行拓扑优化设计。在进行结构拓扑优化时，通过指定拓扑优化模型中的设计域和非设计域来控制结构中的优化和不需要优化的部分，如滚珠丝杠传动系统、滚动导轨等将其设为非设计区域，而横梁方管、底下支架、轴溜板、隔板等设为设计区域。

在以下2 中工况下对横梁进行多刚度拓扑优化:

(1)Y 进给方向最大加速度1.2g 时，横梁的变形。

(2)横梁端部施加2000 N力时横梁的变形，并计算横梁的静刚度()。

在目标函数中将两种工况权重取为相等;同样，也将横梁结构前三阶固有频率的权重值取为相同;在多目标拓扑优化的综合目标函数中，取柔度的权重值为0.4，固有频率权重值为0.6。

在结构进行网格划分后，将设计域每个单元的密度作为设计变量，设置相应的边界条件与工况，并用optistruct 软件中提供的自定义函数来定义多目标拓扑优化的目标函数，利用SIMP 插值方法作为材料模型，结构体积分数作为设计约束。目标函数迭代曲线如图4，体积分数迭代值曲线如图5，经过30 步优化迭代后，最终趋向稳定，拓扑优化得到收敛。最终拓扑优化结果如图6 所示，拓扑优化后结果是以单元密度0～1 来显示，图中深色单元的密度趋近于1，而浅色单元密度趋近于0，单元密度越大表明该构件需要设置加强筋，相反单元密度越小则表明该处的材料可以去掉。因此，横梁方管刚度需要加强，而底下支架材料有盈余，根据拓扑优化结果对横梁进行结构优化设计。

3.3 结构改进设计及分析

根据拓扑优化结果，对横梁结构进行以下改进:在横梁两三角座中间设置加强筋，厚度为5 mm，减小底下支架厚度，由3 mm 变为2.5 mm，优化前后横梁性能参数如表3 所示，在质量基本保持不变的情况下，横梁Y 方向静刚度提高了17.8%，一阶固有频率增加了4.98%，优化效果显著。

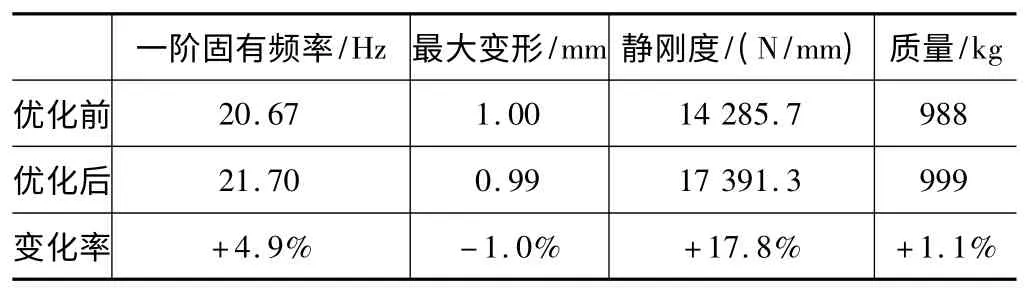
表3 拓扑优化前后横梁性能参数对比

4 结语

本文以数控转塔冲床横梁为研究对象，通过加权欧氏距离法把柔度最小化和模态频率最大化两个目标函数转化为横梁多目标拓扑优化问题，并采用变密度法进行优化求解，基于拓扑优化结果对横梁结构进行改进，提高了横梁静刚度与固有频率，主要结论如下:

(1)针对数控转塔冲床横梁结构的特点，建立了准确的有限元模型，并通过实验验证了有限元模型的正确性，为后续优化设计奠定了基础。

(2)针对单目标拓扑优化无法同时考虑多个目标函数的缺陷，利用加权欧氏距离法将多目标转化为单目标，并建立了多目标拓扑优化的目标函数。

(3)对横梁进行结构改进设计，改进后的横梁在质量基本保持不变的情况下，横梁静刚度提高了17.8%，一阶固有频率增加了4.9%，优化效果显著。

［1］Bendsoe M P，Sigmund O.Topology optimization:theory，methods and applications［M］.Berlin:Springer，2003.

［2］Liu Xinjun，Li Zhidong，Chen Xiang.A new solution for topology optimization problems with multiple loads:the guid-weight method［J］.Science China，2011，54(6):1505-1514.

［3］朱剑峰，林逸，陈潇凯.汽车变速箱壳体结构拓扑优化设计［J］.吉林大学学报，2013，43(3):584-589.

［4］王童，那景新，徐梓雯.基于拓扑优化的某客车空气弹簧支座改进研究［J］.汽车工程，2013，35(9):827-831.

［5］曾金玲，雷雨成，李康.发动机排气制动阀支架的频率优化设计［J］.机械工程学报，2007，43(8):235-238.

［6］Hassania B，Hintona E.A review of homogenization and topology optimization［J］.Computers and Structures，1998，69(6):707-717.

［7］Zbigniew，Sekulski.Multi-objective topology and size optimization ofhigh-speed vehicle-passeng catamaran structure by genetic algorithm［J］.Marine Structures，2010，23(4):405-433.

［8］扶原放，金达峰，乔蔚炜.微型电动车车架结构优化设计方法［J］.机械工程学报，2009，45(9):210-213.

［9］周克明，李俊峰，李霞.结构拓扑优化研究方法综述［J］.力学进展，2005，35(1):69-76.