笼型感应电动机断条故障前后转子电磁力计算及结构静力学分析

谢 颖 冯春爽 杨忠学 刘海松 王 泽

(1.哈尔滨理工大学电气与电子工程学院 哈尔滨 1500802.东北石油大学电气信息工程学院 大庆 163318)



笼型感应电动机断条故障前后转子电磁力计算及结构静力学分析

谢 颖1冯春爽1杨忠学2刘海松1王 泽1

(1.哈尔滨理工大学电气与电子工程学院 哈尔滨 1500802.东北石油大学电气信息工程学院 大庆 163318)

以Y802-2型笼型感应电动机为例，对转子断条故障时的转子电磁应力及结构静力学进行研究。以二维瞬态磁场结果为基础，结合麦克斯韦张量法及洛伦兹力原理，计算得到转子所受磁应力，并给出故障前后转子磁应力随时间的变化规律，此外通过将计算所得转矩均值与实验均值相比较，验证了该电磁力计算结果的准确性。以所得电磁力为载荷，进行电动机稳态情况时转子结构静力学的研究，得到转子故障形变分布。根据故障前后转子电磁力及形变位移的变化可推测出断条故障的进一步演化趋势。

感应电动机 断条故障 有限元法 电磁力 结构静力学 故障形变

0 引言

笼型感应电动机转子导条故障包括导条的断裂和开焊，导致故障的主要原因之一是电动机长期运行中受到的各种力的作用，包括热应力、电磁应力、残余应力和动态应力等，这些力共同作用可导致断条故障的发生。电动机正常运行时，在各种力的作用下，转子导条会出现一定的结构损伤，而断条故障的发生将导致电动机磁场畸变及转子电磁力的分布改变，从而使转子结构形变发生变化，长期如此会使电动机出现疲劳断裂现象，导致多根导条断裂。因此对故障前后转子局部电磁力以及该应力引起的结构形变的研究非常有必要。

目前为止，在电磁力的计算及结构静力学分析方面，国内外学者已做了大量研究工作。文献[1，2]以磁场结果为基础，通过多种算法(包括麦克斯韦张量法、虚位移法及磁化电流法等)求解模型电磁力，分析对比了各种算法的优缺点，并得出磁场计算结果是影响电磁力计算结果准确性的重要因素的结论。文献[3]分析了极化模型电磁力算法的理论推导及物理意义，并以继电器为例进行了研究。文献[4，5]以不同算法计算得到的电磁力为载荷进行了结构形变计算，并比较了得到的结果。文献[6，7]基于虚位移原理对汽轮发电机的局部电磁力进行了计算，并提出了一种新算法。文献[8]通过麦克斯韦张量法建立了无轴承开关磁阻电动机的电磁力数学模型。文献[9]运用麦克斯韦张量法计算了永磁及铁磁材料电磁力，论述了电磁力密度与单元空间电磁力的意义。文献[10]计算了汽轮发电机端部的电磁场分布，采用三维有限元法对端部力密度进行了计算，得到了端部电磁力的精确分布，为后续优化工作奠定了基础。文献[11，12]计算了大型感应电动机单相短路故障时的动态电磁力以及某笼型感应电动机径向电磁力。文献[13]利用有限元法对电动机进行了动力学及应力位移仿真，根据所得数据进行了转子的强度和刚度校核，并分析了转子的主要破坏形式和危险位置；此外结构静力学分析可进一步深入到强度分析及结构优化设计中[14，15]。

本文以笼型感应电动机磁场计算结果为基础，利用麦克斯韦张量法和洛伦兹力原理对电动机断条前后的转子局部电磁力进行求解，并分析了故障前后电磁力随时间的变化规律。基于转子局部电磁力计算结果，利用有限元法对转子结构静力学进行研究，得到了健康及故障转子的形变图及形变曲线，进而预测出转子导条进一步的断裂位置。

1 转子电磁力计算与分析

1.1 样机测试平台

本文以一台Y802-2型笼型感应电动机为例进行研究，对样机进行了转矩测量实验，分别测量转子健康和两根断条时的转矩均值，图1a、图1b给出了健康转子及断条转子，实验平台如图1c所示，实验使用转矩转速测试仪测量样机输出转矩，测试过程中保证正常及故障电动机输出功率均为额定功率。

图1 测试平台Fig.1 Test table

1.2 样机参数及电磁场计算方程

样机主要参数如表1所示。计算中忽略磁场在轴向方向的变化，将三维空间磁场简化为二维问题，磁矢量方程如式(1)所示[16]，该模型不计定、转子铁心产生的涡流，且认为转子硅钢片和导条之间没有电流通过。

表1 样机参数Tab.1 Parameters of the prototype motor

(1)

根据文献[16]，通过修正模型中导条的磁导率和电导率计及转子斜槽和端环对二维磁场的影响，公式为

(2)

(3)

式中：σ′为修正后的转子导条电导率；σ为实际铸铝电导率；R′2b为导条电阻值；R′2r为端环电阻值；μ′2为修正后的转子导条磁导率；μ0为空气磁导率；x′2b为转子槽漏抗；x′2r为转子端部漏抗；x′2k为斜槽漏抗。

1.3 磁场计算结果及分析

图2为样机额定负载运行时故障前后的磁通密度分布，图中已标出断条位置。健康电动机磁场呈对称分布，故障发生后磁场的对称性被破坏，且断条位置附近出现了较高的磁饱和现象。

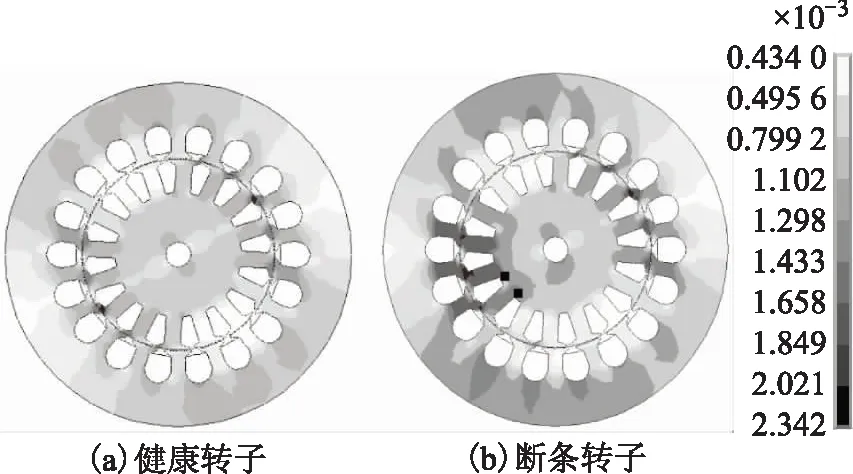
图2 样机额定负载运行时断条前后磁通密度分布Fig.2 Distribution of magnetic flux density of the motor operating under rated load before and after broken bars

1.4 感应电动机转子电磁力计算

1.4.1 电磁力计算分类

根据转子受力部位和受力处交界面不同，本文将转子所受电磁力分为3类：第1类为转子硅钢片与导条交界处产生的电磁力，称之为槽一周法向力，如图3a、图3b所示fn1、fn2；第2类为转子硅钢片与空气交界处产生的电磁力，称之为转子径向力，即图6中的fr1和fr2；第3类为转子导条受到的洛伦兹力，如图8中的fbr和fbt。规定样机运行方向为顺时针方向。

1.4.2 电磁力计算方法

麦克斯韦张量法是用等效的面积力代替体积力来计算交界面上的电磁应力，本文利用该方法计算铁磁媒质受到的电磁力，如式(4)所示[16]；利用式(5)计算转子导条所受洛伦兹力[16]。

(4)

式中：B1n、B2n为不同媒质交界面处的法向磁通密度值；B1t、B2t为切向磁通密度值；μ1、μ2为两种媒质的磁导率；s代表物体的外表面。

Fe=lSeJe×Be

(5)

式中：Fe为单元所受洛仑兹力矢量；l为导条轴向长度；Se为单元面积；Je为单元电流密度矢量；Be为单元磁通密度矢量。

1.5 转子电磁力计算结果及分析

1.5.1 实验值与仿真值对比

由转子电磁力的计算结果，可得到作用在电动机转子上的整体转矩值。为了验证仿真的准确性，将电动机在健康及断条情况运行时的转速及转矩的计算均值与实验均值进行对比，如表2所示，为了便于比较，实验测试过程中保证样机在各种情况下输出功率均为1.1 kW，此条件下故障情况时的转速有所降低，且电磁转矩增加，表中计算及实验得到的结果符合这一情况。

表2 电磁转矩及转速值对比Tab.2 Comparison of electromagnetic torque and speed value

1.5.2 转子槽一周法向力分布

图3为转子槽一周法向力的分布示意图。图3a中，将ab、bc、cd及do区分别定义为槽口、靠近槽口、靠近槽底及槽底，图3b中，ef、fg、gh及ho区定义同图3a。图4、图5中标出了a～h及o点的位置，在各拐点处电磁力变化较大。图4为额定负载运行时断条前后转子槽前侧电磁力分布。由图4a可知，健康情况时转子槽前侧的ab及bc区所受电磁力较大，其他区域除a、b、c、d点外受力不大；图4b为故障后顺时针临近断条处的转子槽前侧受力情况，相较于图4a可知，ab区受力有所变化，bc及do区受力变化不大(除拐点外)，cd区磁应力明显增大。图5为断条前后转子槽后侧所受电磁力分布，断条后磁应力变化规律与前侧相似，但与前侧受力情况相比，数值较小。

1.5.3 转子径向力分布

图6为转子径向力的作用位置。图7为断条前后转子径向电磁力的分布，图中标出了图6中关键点的位置，其中图7b为顺着样机旋转方向断条和临近断条之间圆弧上的径向电磁力分布情况。由图7可知，靠近槽前侧圆弧所受应力值大于槽后侧，即ia段受力大于ej段，断条时转子径向力大于健康情况。

图3 转子槽一周法向力分布位置示意图Fig.3 Schematic diagram of normal electromagnetic force distribution on the border of the rotor slots

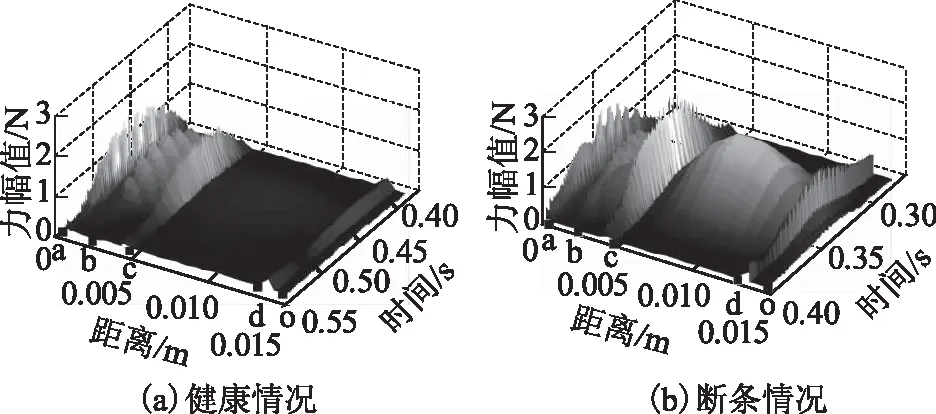
图4 断条前后转子槽前侧槽一周法向力分布Fig.4 Distribution of normal electromagnetic force on the front side border of the rotor slots before and after broken bars

图5 断条前后转子槽后侧槽一周法向力分布Fig.5 Distribution of normal electromagnetic force on the rear side border of the rotor slots before and after broken bars

图6 转子径向力分布位置示意图Fig.6 Schematic diagram of radial electromagnetic force on rotor

图7 断条前后转子径向力分布Fig.7 Distribution of radial electromagnetic force on rotor before and after broken bars

1.5.4 转子洛伦兹力分布

图8 转子洛伦兹力的切向和法向力Fig.8 Tangential and normal of the rotor lorentz force

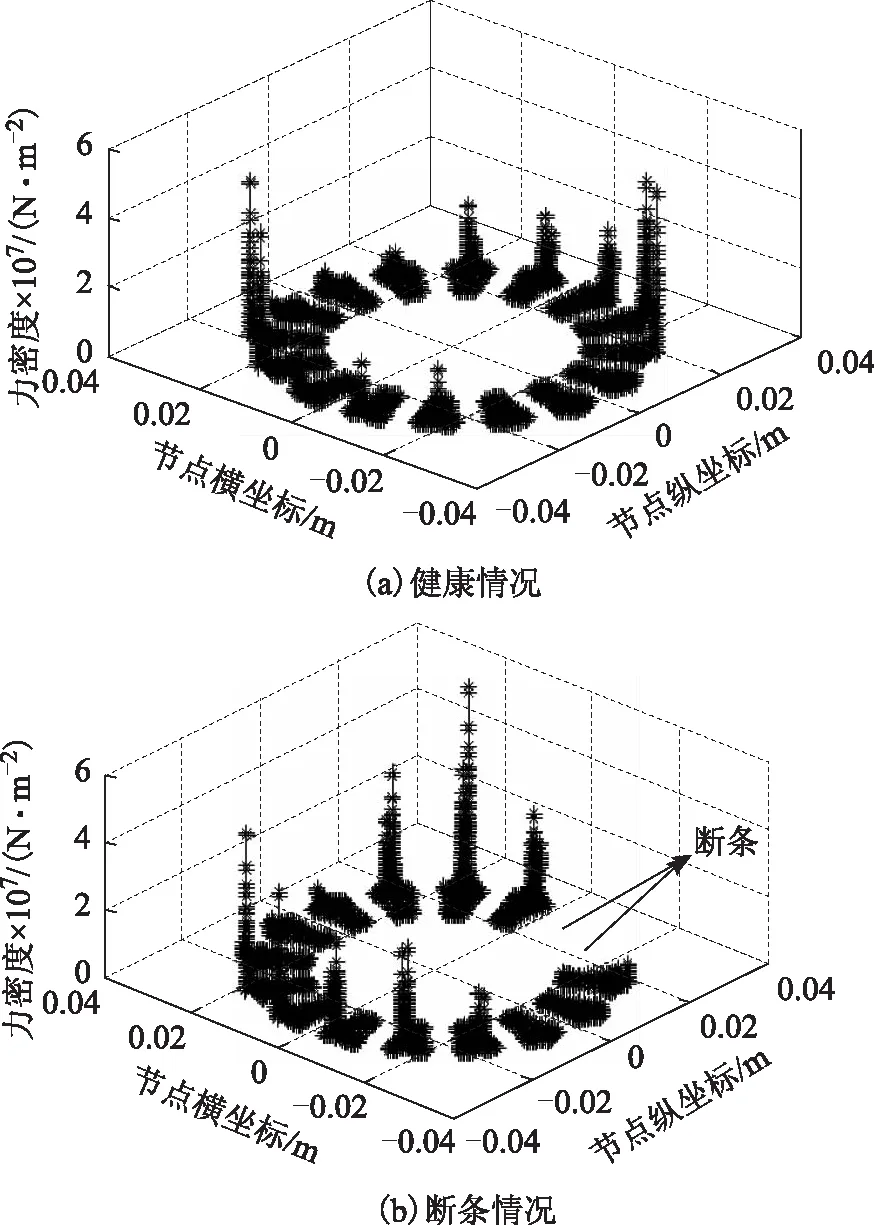
图9 断条前后转子洛伦兹力分布(t=0.38 s)Fig.9 Distribution of the rotor lorentz force before and after broken bars (t=0.38 s)

转子洛伦兹力的切向和法向力如图8所示。图9为电动机在额定负载运行情况下，0.38 s时断条前后转子导条洛仑兹力密度分布情况。由图9可知，某一时刻下各导条所受洛仑兹力并不相同，且每一根导条受力幅值较大的位置出现在导条顶部。转子健康运行时洛伦兹力分布对称，故障发生后断条处没有该力的作用，断条位置顺着旋转方向一侧的导条产生了不同程度的洛仑兹力畸变，且非对称性明显，即与断裂导条相邻的导条所受洛伦兹力增加明显，这种交替变化且增加明显的洛伦兹力将会增大导条疲劳断裂的可能性。

2 转子结构静力学有限元计算及分析

2.1 结构力学

结构静力学分析是指不考虑惯性和阻尼特性，不考虑随时间变化的载荷等因素的条件下，系统在稳定载荷作用下对结构进行应力、应变和位移的分析，但允许有如重力和离心力等稳定的惯性载荷作用，随时间变化的载荷可等效为静态载荷，进行静态分析。本文对笼型转子结构静力学进行研究，以上述计算结果中某些时刻的电磁力作为三维结构静力学载荷，从而得到故障前后转子的形变情况。

结构静力学模型中建立了端环，完善了转子模型。本文并未深入研究端环的受力情况，主要原因有电动机端部区域边界和电流分布较为复杂，且端部磁场是时变场，它在有关部件中会感应涡流，且端部磁场在计算时会由于一系列原因而产生误差，包括模型简化、计算方法、网格剖分不够精确等，这样更降低了端部磁场计算的准确性，另端部电磁力作用较小，对模型的形变影响不大，因此本文不单独计算端部的受力情况[17，18]。此外在二维电磁场计算过程中，通过式(2)、式(3)计及了端部的影响，参见文献[16]。

在工程计算中对于刚体的微小形变通常视为弹性形变，因此本文应力和形变的关系遵循弹性力学的规律。结构静态分析的整体平衡方程如式(6)或式(7)所示，通过方程(6)便可得到节点位移矢量u。

Ku=F

(6)

或

Ku=Fa+Fr

(7)

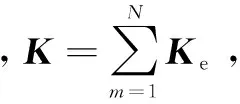
2.2 结构静力学计算模型

对有限元分析来说，确定有限元单元类型非常重要，单元类型的选择不仅影响网格的合理划分，而且对求解的精度影响很大。考虑到转子模型的复杂程度、精度要求以及计算求解时间等实际因素，采用Solid186空间实体单元，以电磁场计算的二维模型网格为基础，运用延伸分网的方法生成三维模型和网格，以此实现载荷加载时节点的对应，建立端环并分网，在导条与端环接触的位置添加接触单元，以达到使两者形变连续的目的。在转子铁心内圆表面施加面约束，以代替转轴的作用。

为了缩短计算时间，分别计算槽一周法向力和径向力共同作用及洛伦兹力单独作用的情况。选取0.395s时健康和断条电磁力数据进行计算，载荷施加示意图如图10、图11所示。

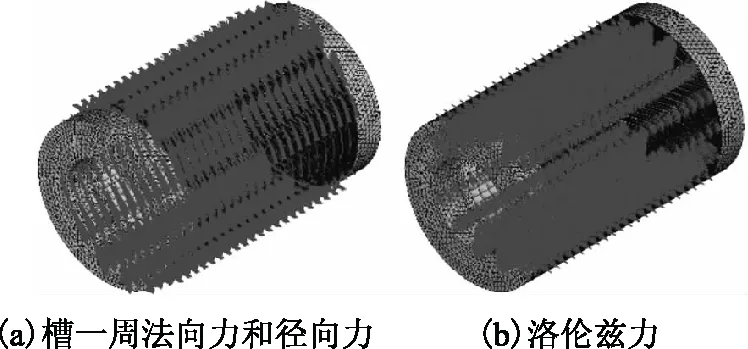
图10 转子电磁力载荷轴向示意图Fig.10 Axial direction schematic diagram of electromagnetic force on the rotor

图11 转子电磁力载荷x、y方向示意图Fig.11 x、y direction schematic diagram of electromagnetic force on the rotor

2.3 转子结构静力学结果分析

2.3.1 计及槽一周法向力和转子径向力的计算结果

图12为槽一周法向力和转子径向力共同作用下转子断条前后形变图，图中健康转子形变对称，断条发生后，顺时针临近断条的区域形变加大，从端环处也可看出形变失去对称性。转子导条及端环形变如图13所示，导条和端环连接处形变连续，此处也是形变较大位置，断条后这一现象更加明显，形变最大值为1.11×10-7m。

为了更清楚的观察转子的形变大小和趋势，取图12模型的部分数据点做成周向和轴向位移曲线图，所取数据点如图14所示。周向图分别取每根导条上各槽相同位置点，图15为断条前后转子槽前侧A1、B1、C1三点的形变曲线，健康时形变呈两极对称分布，因此曲线表现为周期变化，A1及B1处形变较大，C1处形变相对较小。断条后槽前侧形变大于健康情况，断条及靠近断条处各点的形变明显增大，其中A1及B1形变增量大于C1处，形变曲线呈非周期变化。断条前后转子槽后侧的形变曲线的变化趋势与槽前侧相近(见图16)。轴向图取包括端环在内的同一轴向上的数据点，如图17所示，导条和端环连接处形变较大，且断条情况下的形变大于健康情况。

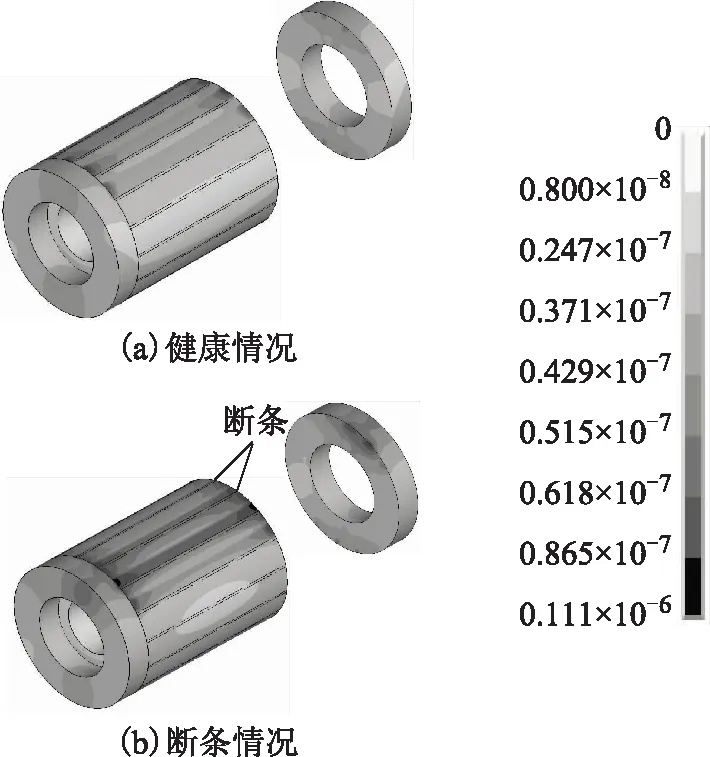
图12 断条前后转子形变云图Fig.12 The displacement of the rotor before and after broken bars

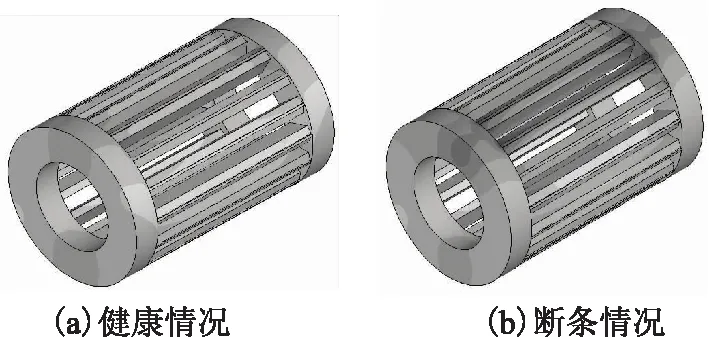
图13 断条前后转子导条及端环形变云图Fig.13 The displacement of the rotor bar and ending before and after broken bars

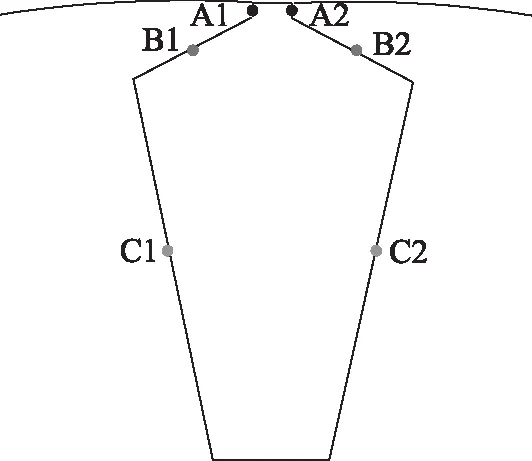
图14 位移曲线数据点的选取Fig.14 The data points of the displacement curve

图15 转子槽前侧周向形变曲线Fig.15 Circumferential displacement curve of the front side of rotor slots

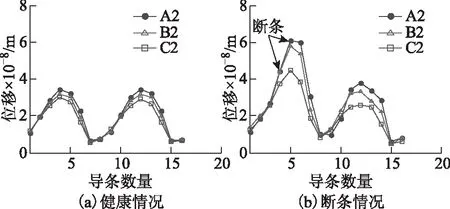
图16 转子槽后侧周向形变曲线Fig.16 Circumferential displacement curve of the rear side of rotor slots

图17 转子轴向形变曲线Fig.17 Axial displacement curve of the rotor

2.3.2 计及洛伦兹力计算结果

洛伦兹力单独作用的转子断条前后形变图如图18、图19所示，由图可知，断条后形变大于断条前，且呈不对称分布，断条附近导条形变增加，最大形变仍出现在端环和导条连接处，大小为8.84×10-10m，所以洛伦兹力作用明显小于另两种力共同作用。

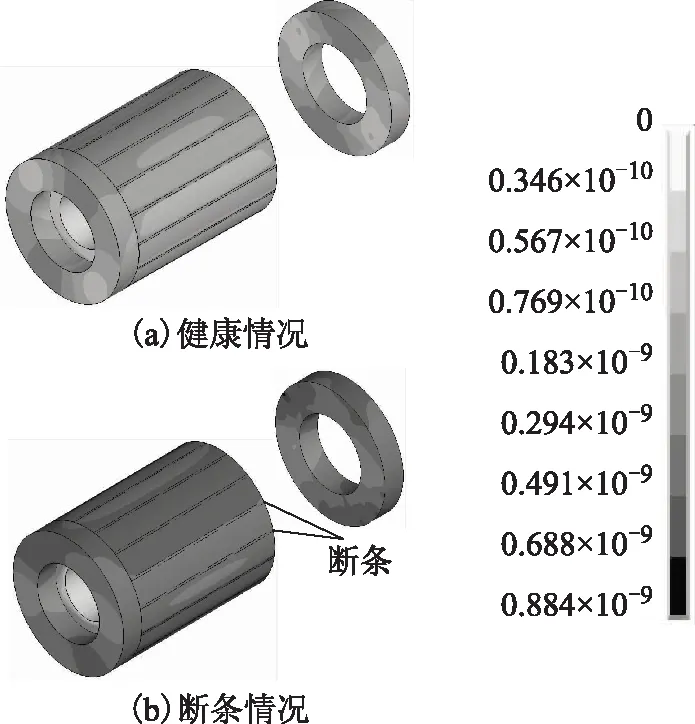
图18 断条前后转子形变云图Fig.18 The displacement of the rotor before and after broken bars

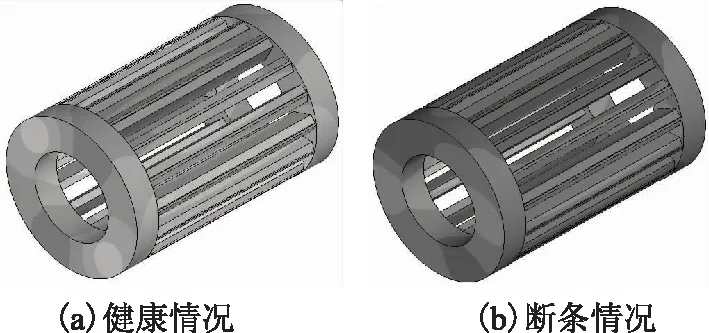
图19 断条前后转子导条及端环形变云图Fig.19 The displacement of the rotor bar and ending before and after broken bars

图20为洛伦兹力形变曲线所取数据点的位置，周向和轴向形变曲线如图21、图22所示。图21中，断条处不受洛伦兹力作用，但会因模型形变产生的压力作用而发生一定的变形，转子健康时形变较小，故障后断条附近导条形变发生变化破坏了形变周期性。图22中，槽口及靠近槽口区域在断条发生后形变明显变大。

图20 位移曲线数据点的选取Fig.20 The Selection of data points of displacement curve

图21 洛仑兹力转子周向形变曲线Fig.21 Circumferential displacement curve of the rotor by the lorentz force

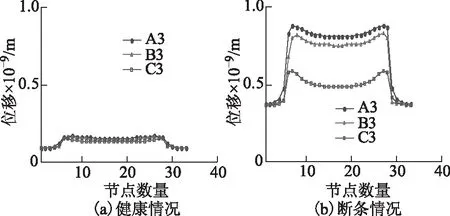
图22 洛仑兹力转子轴向形变曲线Fig.22 Axial displacement curve of the rotor by the lorentz force

3 结论

本文结合麦克斯韦张量法和洛伦兹力原理，运用有限元法计算了笼型异步电动机转子断条前后的电磁力，通过转矩计算值与实验值的比较，确定了电磁应力结果的正确性。将计算所得电磁力作为载荷分析笼型转子断条故障前后形变规律。根据上述计算和分析得出针对Y802-2型2极电动机的结论如下：

1)电动机非故障运行时，在转子槽的槽口两侧圆弧、槽口及靠近槽口处所受电磁力较大，槽前侧受力大于槽后侧，故障后顺时针临近断条的转子槽口及靠近槽底处受力增加；洛伦兹力在导条顶部作用明显，正常运行时应力呈两极对称分布，故障后断条附近导条所受应力发生畸变且增大明显。

2)在转子槽一周法向力和转子径向力的共同作用下，健康转子形变对称，槽口及靠近槽口处形变较大，端环和导条连接处形变连续且形变量大于轴向其他位置，故障后断条附近导条的转子槽口及靠近槽口处形变增加，轴向上形变也有所增加；洛伦兹力单独作用下，健康转子形变较小，故障后断条附近的导条顶部形变明显增加。

3)电动机正常运行时，转子槽口及靠近槽口处所受应力和形变较大，故障发生后这一情况更加明显，尤其电动机在起动过程中转子电磁应力和形变的增量远大于稳定运行时，在应力低于材料屈服应力和强度极限的前提下，这种增加明显的电磁力和形变将会增大导条顶部疲劳断裂的可能性，造成连续断条的发生。

4)基于转子电磁力及结构静力学的研究和分析，可推测出进一步断条位置为顺时针临近断条的导条顶部，且易发生在端环和导条连接处，此结论与工程实际情况相符合。

继本文研究内容之后，将对转子进行瞬态动力学的计算，以得到转子形变随时间的变化及应力应变关系。结合转子导条材料的S-N曲线及疲劳损伤规则等对转子进行疲劳分析，以得到本文笼型感应电动机的疲劳损伤系数及疲劳寿命分布，估测笼型感应电动机的使用寿命，为工程实用提供参考。

[1] Mizia J，Adamiak K，Eastham A R，et al.Finite element force calculation comparison of methods for electric machines[J].IEEE Transactions on Magnetics，1988，24(1)：447-450.

[2] Ren Z.Comparison of different force calculation methods in 3d finite element modelling[J].IEEE Transactions on Magnetics，1994，30(5)：3471-3474.

[3] Kovanen T，Tarhasaari T，Kettunen L.Computation of local electromagnetic force[J].IEEE Transactions on Magnetics，2011，47(5)：894-897.

[4] Lee S H，Park I H，Lee K S.Comparison of mechanical deformations due to different force distributions of two equivalent magnetization models[J].IEEE Transactions on Magnetics，2000，34(4)：1368-1372.

[5] Lee S H，Han S J，Choi H S，et al.Magnetic force distributions in saturated magnetic system using magnetic charge method and other methods[J].IEEE Transactions on Applied Superconductivity，2004，14(2)：682-685.

[6] 李志强，罗应立，蒙亮.基于有限元的虚位移原理在汽轮发电机局部电磁力计算中的应用[J].中国电机工程学报，2007，27(15)：47-52. Li Zhiqiang，Luo Yingli，Meng Liang.The calculation of local magnetic force in turbo-generator with FEM based virtual work principle[J].Proceedings of the CSEE，2007，27(15)：47-52.

[7] 李志强，罗应立.基于有限元和虚位移原理的电机内电磁力密度计算新方法[J].中国电机工程学报，2009，29(3)：71-77. Li Zhiqiang，Luo Yingli.New method of magnetic force density computation for turbo-generator based on finite element method and virtual work principle[J].Proceedings of the CSEE，2009，29(3)：71-77.

[8] 曹鑫，邓智泉，杨钢，等.无轴承开关磁阻电机麦克斯韦应力法数学模型[J].中国电机工程学报，2009，29(3)：78-83. Cao Xin，Deng Zhiquan，Yang Gang，et al.Mathematical model of bearingless switched reluctance motors based on maxwell stress tensor method[J].Proceedings of the CSEE，2009，29(3)：78-83.

[9] Kovanen T，Tarhasaari T，Kettunen L.Localization of electromagnetic force based on material models[J].IEEE Transactions on Magnetics，2012，48(1)：13-17.

[10]Stancheva R D，Iatcheva I I.3-D electromagnetic force distribution in the end region of turbogenerator[J].IEEE Transactions on Magnetics，2009，45(3)：1000-1003.

[11]梁艳萍，刘金鹏，陈晶.大型感应电动机单相短路故障动态力计算[J].中国电机工程学报，2012，32(9)：109-115. Liang Yanping，Liu Jinpeng，Chen Jing.Dynamic electromagnetic force calculation for single-phase short circuit fault of large induction motors[J].Proceedings of the CSEE，2012，32(9)：109-115.

[12]王荀，邱阿瑞.笼型异步电动机径向电磁力波的有限元计算[J].电工技术学报，2012，27(7)：109-117.Wang Xun，Qiu Arui.Finite element calculation of radial electromagnetic force wave in squirrel-cage asynchronous motors[J].Transactions of China Electrotechnical Society，2012，27(7)：109-117.

[13]毛文贵，傅彩明，谭加才.大功率立式电机转子有限元结构分析和优化[J].电机技术，2007(1)：22-24. Mao Wengui，Fu Caiming，Tan Jiacai.FEM structure analysis and optimization of vertical motor rotor[J].Electric Motor Technology，2007(1)：22-24.

[14]程文杰，耿海鹏，冯圣，等.高速永磁同步电机转子强度分析[J].中国电机工程学报，2010，32(27)：87-94.Cheng Wenjie，Geng Haipeng，Feng Sheng，et al.Rotor strength analysis of high-speed permanent magnet synchronous motors[J].Proceedings of the CSEE，2010，32(27)：87-94.

[15]王剑，胡锡幸，郭吉丰.基于柔性板簧的三自由度球形超声波电机静力学建模与分析[J].电工技术学报，2014，29(3)：125-131. Wang Jian，Hu Xixing，Guo Jifeng.Statics modeling and analyzing of three-degree-of-freedom spherical ultrasonic motors with the spiral spring[J].Transactions of China Electrotechnical society，2014，29(3)：125-131.

[16]汤蕴璆.电机内的电磁场[M].2 版.北京：机械工业出版社，1998：265-278，341-367.

[17]梁艳萍，王鸿鹄，张建涛.空冷汽轮发电机端部电磁场与涡流损耗研究[J].电机与控制学报，2010，14(1)：29-34. Liang Yanping，Wang Honghu，Zhang Jiantao.Research of end fields and eddy current losses for air-cooling steam-turbo-generator[J].Electric Machines and Control，2010，14(1)：29-34.

[18]黄涛，阮江军，张宇娇，等.多相异步电机端部绕组电磁与结构耦合场分析[J].大电机技术，2011(3)：1-4. Huang Tao，Ruan Jiangjun，Zhang Yujiao，et al.Magneto-structural coupling field analysis on the end winding of multi-phase asynchronous motor[J].Large Electric Technology，2011(3)：1-4.

Electromagnetic Force Calculation and Structural Static Analysis on the Rotor of Squirrel-cage Induction Motors Before and After the Broken Bars Fault

XieYing1FengChunshuang1YangZhongxue2LiuHaisong1WangZe1

(1.School of Electrical & Electronic Engineering Harbin University of Science and Technology Harbin 150080 China 2.School of Electrical Engineering&Information Northeast Petroleum University Daqing 163318 China)

Takingthe Y802-2 type squirrel-cage induction motor asan example，the electromagnetic force and structural static on the rotor are researched when the motor operates with the broken bars fault.Based on the results of the two-dimensional transient magnetic field，the magnetic force iscalculated by the Maxwell tensor method and the principle of the Lorentz force.Then the change patterns with time of the rotor electromagnetic force are given before and after the broken bars fault.In addition，the validity of the calculated results is confirmed through comparing with the ones measuredin the experiments.Using the calculated electromagnetic forceas the load，the structural static of the rotor in the steady state is studied afterwards.The fault deformation distribution on the rotor is then achieved.The further evolution trend of the broken bars fault can be speculated by the rotor electromagnetic force and the change of displacement before and after the fault.

Induction motor，broken bars fault，finite element method，electromagnetic force，structural static，fault deformation

国家自然科学基金(51107022)、黑龙江省政府博士后科研启动项目(LBH-Q12061)、黑龙江省普通高等学校新世纪优秀人才培养计划(1252-NCET-015)、黑龙江省自然科学基金(E201443)、人社部留学人员科技活动项目择优资助项目和哈尔滨市科技创新人才研究专项资金项目(RC2014QN007005)资助。

2015-01-30 改稿日期2015-06-02

TM343

谢 颖 女，1974年生，教授，硕士生导师，研究方向为电机内电磁场、温度场、振动噪声计算及感应电动机故障诊断及检测。(通信作者)

冯春爽 女，1991年生，硕士研究生，研究方向为故障电机电磁场、结构学、疲劳断裂分析。