全数字硬件化正交锁相环建模与分析
刘亚静 范 瑜
(北京交通大学电气工程学院 北京 100044)
全数字硬件化正交锁相环建模与分析
刘亚静 范 瑜
(北京交通大学电气工程学院 北京 100044)
针对FPGA/ASIC的全定制特性带来的字长优化问题,提出一种基于FPGA/ASIC的全数字硬件化正交锁相环字长建模方法。首先,利用稳定性判据和卷积分别建立系数和内部变量的整数字长模型;然后,依据系统灵敏度及L2范数理论分别对系数和内部变量的小数字长建模,从而只需设定系数准确度指标ε和变量准确度指标ζ,即可设计出满足要求的全数字硬件化正交锁相环,保证在消耗最少资源的前提下,有效避免溢出错误和抑制有限字长效应;最后通过实验,验证了所提模型的可靠性。
正交锁相环 全数字硬件化 字长模型 有限字长效应
0 引言
数字正交锁相环已成为电网电参数检测、电机位置检测与估计等应用领域的标配算法,主要分为基于DSP/MCU的全数字软件化方案和基于FPGA/ASIC的全数字硬件化方案。后者因具有全定制及并行等特性而成为实现高性能锁相环的首选。文献[1-3]对全数字硬件化进行了初步研究,但仍未引起足够重视。全数字硬件化的难点是算法模块参数化,即对算法模块进行包含时序、字长等属性的参数化,使其运算时间、资源消耗等参数明确化,避免设计的盲目性[3]。
字长属性参数化的首要问题是实现方式的选择。定点实现比浮点具有更快的速度、更低的功耗及更小的芯片面积,是实现全数字硬件化算法的首选。但一定字长所表示的动态范围和准确度是一对矛盾体,存在有限字长效应。当采用较高的离散化频率或实现较高阶数的算法时,有限字长效应会使系统性能明显下降,增加字长可削弱有限字长效应的影响,但会占用较多资源[3],因此非常有必要对其进行分析,以使在满足性能要求的前提下,FPGA/ASIC消耗的资源最小化。
微电子领域的学者采用基于分析和仿真的定点化方法,借助各种优化算法进行字长优化[4-6]。文献[4]提出采用区间算术进行信号动态范围分析,采用仿真方法确定信号准确度。文献[5]采用仿射算术分析信号范围和准确度,但在处理反馈循环次数未知或无限的闭环反馈算法时仍存在困难。控制领域的相关学者从系统的角度研究数字控制器的有限字长效应,通过不同的测度和设计方法对数字控制器的结构进行优化设计[7-9]。文献[8]提出了一种新的稳定性度量对数字控制器进行优化设计,能更准确地衡量系统的稳定性及有限字长效应。文献[9]提出了闭环系统的ML2测度,通过求取其最小值实现系统结构的优化。但主要是从理论角度寻找有限字长效应最小的控制器结构,缺少具体实现的讨论。电机控制领域的学者从工程实践角度探索电机控制算法的FPGA实现,包括无位置传感控制[10]、交流伺服控制[11]、电机电流预测控制器[12]以及数字电源的控制[13],文献[14,15]甚至提出了FPGA应用于工业控制时的设计指导思想。但相关学者主要研究FPGA在电机控制方面的应用,基本未考虑实际应用中如何描述和抑制有限字长效应。
文献[1,2]针对上述问题,从系统、综合的角度对一种全数字闭环算法(锁相环)进行详细分析,文献[1]建立了全数字硬件化轴角转换模型,确定了不同模数转换准确度时的系数整数字长和变量小数字长。文献[2]指出降低离散周期T可减小延迟,提高系统带宽,但会增加表示字长,意味着消耗更多的寄存器和布线资源,这样就要求实现跟踪性能和芯片资源消耗之间的最佳平衡,而前提就是要能够完备、定量的描述资源消耗模型,为全数字硬件化锁相环优化设计提供基础。
本文提出一种全数字硬件化正交锁相环建模方法:考虑反馈滞后一拍现象,利用稳定性判据建立系数整数字长模型;依据实际输入信号性质,利用卷积描述变量整数字长模型;依据系统灵敏度理论,建立系数小数字长模型;利用L2范数建立变量小数字长模型,从而完备地描述了锁相环的字长消耗情况。最后通过实验,证明了所提模型的可靠性。
1 全数字硬件化锁相环计算图
采用计算图对锁相环进行建模。计算图H(V,S,A)将基本计算单元(如加、减、乘等)及模型的输入及输出端口定义为节点vi(i 计算图中的S在FPGA中可由布线单元或逻辑单元实现,对应的集合分别为S1、S2,且满足S1⊂S,S2⊂S。布线资源事先铺设在路由通道,本文不将其作为资源消耗的主要指标。逻辑单元通常由一定数量的寄存器、查找表以及选择器组成。为了减小竞争冒险,一般采用同步设计方法,需要利用寄存器对相关有向连线(变量信号)进行缓存,大量实践表明,相关算法最消耗寄存器资源,而寄存器消耗量与所有变量信号的表示字长是对应的,因此,只需求出内部所有信号的表示字长即可。锁相环的计算图如图1所示,图中仅标示出集合S2内的元素。 图1 全数字硬件化锁相环模型框图Fig.1 Block diagram of all-digital full-hardware PLL 根据锁相环内部信号性质的不同,将其分为系数信号和变量信号,本文分别对其建立字长模型。 2.1 整数字长建模分析 本节研究系数整数字长和变量整数字长模型。整数字长主要由动态变化范围决定,而系数整数字长和变量整数字长的确定略有区别。本文首先利用稳定性判据确定系数整数字长,然后依据卷积求得内部变量的整数字长。 2.1.1 系数整数字长模型 当锁相环进行物理实现时,反馈通道会引入滞后一拍效应,依据文献[2],得离散锁相环表达式为 (1) 式中:b0=kpT/2+kiT2/4,b1=kiT2/2,b2=kiT2/4-kpT/2,a1=kpT/2+kiT2/4-2,a2=kiT2/2+1,a3=kiT2/4-kpT/2;kp为比例增益;ki为积分增益;T为离散周期。 根据Z域稳定性判据,得系统的稳定性条件为 (2) 可得比例和积分系数的整数字长表达式为 (3) 2.1.2 变量整数字长模型 内部变量发生上溢错误有可能使系统在较大初始条件下无界,甚至引起系统的不稳定,因此必须对系统内部变量的取值范围进行分析,以确定各变量的整数字长,防止产生向上溢出。 内部变量sj(j (4) 式中:hIj(n)为输入v1到内部变量sj的脉冲响应函数;Z域传递函数为HIj(z)。 本文仅考虑物理可实现的因果系统,当n<0时,hIj(n)=0。 对于正常的系统,阶跃信号已经是非常苛刻的输入信号了,因此本文选择输入信号为 v1(n-k)=QI (5) 式中QI为输入信号幅值。 则可将式(4)转换为 (6) 依据式(6)可得内部变量sj的整数字长为 (7) 由图1可知,锁相环的内部变量有8个。输入为两相正交信号,定义为一个矢量信号s1,字长由前一级决定。锁相环输出变量为s8,s2和s3分别表示比例与积分系数,其余4个为系统内部信号,且s7的整数字长等于s4和s6的最大值,则从输入到各变量的Z域脉冲传递函数HIj(z)以及在式(2)的约束下的各变量所需最大字长(IWsj)max如表1所示。 表1 内部变量整数字长Tab.1 The integer word-lengths of the state variables 2.2 小数字长建模分析 当算法进行全数字硬件化实现时,不同的实现结构会产生不同的结果,这主要是由控制器系数的量化误差和信号的量化误差引起。系数的大小决定了系统的结构特性,量化误差可看作是系数的摄动,可利用系统灵敏度理论研究系数的量化误差,信号的量化误差则用概率模型来完整地描述。 2.2.1 系数小数字长模型 当进行实际物理实现时,将kpT与kiT2作为系统的两个系数。依据灵敏度的定义,可得两个系数的微小变化引起的锁相环的极点变化分别为 (8) 式中:n为离散系统阶数;pi、pj为式(1)的极点。 系数变化所引起的极点变化要求满足 (9) 式中ε为系统极点变化的相对误差。 将式(8)带入式(9)可得比例系数和积分系数的变化需满足 (10) 式中 可得比例和积分系数的小数字长表达式为 (11) 由式(10)和式(11)可知,需确定δPi和δIi的最小值以及ε。ε是根据系统性能指标设置的,则本文主要阐述δPi、δIi最小值的确定方法。 首先求得式(1)的极点,然后将其带入δPi、δIi的表达式中,如表2所示。 表2 δPi、δIi表达式Tab.2 The expressions of δPi,δIi 表2中,p1为实根,p2、p3为共轭复根,则应有δP2=δP3,δI2=δI3。δPi、δIi是kpT、kiT2的函数,经分析可知在边界取最小值。本文根据系统稳定性来确定边界,所得到的kpT和kiT2可保证在整个稳定范围内均能满足极点准确度要求,然后求得在此边界约束下,δPi、δIi的最小值分别为 (12) 2.2.2 变量小数字长模型 当采用定点格式进行数字实现时,为避免字长“爆炸式增长”,需要截断或舍入操作,从而产生量化误差,通常将其等效为与信号序列不相关的白噪声,然后采用概率模型来描述。设量化前的数字量为(IW1,FW1),量化后的数字量为(IW1,FW2),当采用二进制补码表示运算的数据时,可得内部信号变量的量化误差的方差为 (13) 在实际系统中,各变量之间存在数据交换,造成上一级信号变量的量化误差影响下一级信号变量,使得信号变量的准确度不等于分辨率。通常根据文献[2]所提的误差传播路径范数来确定数据传输过程中受到的影响。因此,为了描述误差源i对系统输出端的影响,不但需要误差源i的误差表达式(13),还要有误差的传播模型公式,为 (14) 将式(13)带入式(14)中,可得内部变量si的小数字长满足 FWsi=[log2(rimax/ζ)] (15) 式中:FWsi为系统内部变量的小数字长;ζ为设定的准确度指标。 由图1可知,s2和s3分别表示比例与积分系数,小数字长已由前面的系数小数字长模型确定,因此只需确定变量s1、s4、s5、s6、s7、s8的小数字长即可。当对上述变量进行量化操作时,会产生相应的误差e1、e4、e5、e6、e7、e8。 锁相环的HOi(z)表达式如表3所示,设定ζ=10-3时,内部各变量的小数字长如表3所示。 表3 内部变量小数字长Tab.3 The fraction word-lengths of state variables 为验证本文所提模型的正确性,需排除与本文研究无关的影响因素(如模数之间相互转换时引入的误差),因此,首先利用Matlab分别验证各模型的正确性,然后,按照所提模型设计锁相环,并利用Xilinx的XC3S1200E实现,得到实验结果,从而验证建模方法的正确性。 本文所提的模型中主要包括两个参数ε和ζ,其中,通过设定式(9)中的极点相对变化误差的极值ε来间接确定系统系数的准确度。ζ代表算法内部各误差源对输出的影响强弱,是概率统计意义的一个参数,ζ越小,意味着误差源对输出的影响越小,如ζ=10-3时,代表算法内部误差源使系统输出产生0.1%的误差。 3.1 仿真验证结果分析 图2 锁相环稳定性仿真验证图形Fig.2 The simulation result of PLL’s stability 给锁相环输入阶跃信号,遍历满足式(2)的kpT与kiT2,得到与之对应的内部各变量值,然后将其分别与表1所确定的字长表示范围相比较,验证所提变量整数模型的正确性。由前面分析可知,本部分只需确定s4、s5、s6、s8的整数字长。图3给出了内部各变量值关于kpT与kiT2的曲线。图中的设定值即为2(IWsj)max-1,可见,在稳定域范围内,内部变量值均小于设定值,变量整数字长模型可保证不会发生向上溢出错误。 图3 变量整数字长仿真验证结果Fig.3 The integer word-lengths of state variables 3.2 小数字长模型的仿真验证 图4 kpT的微小摄动引起的极点相对误差的验证结果Fig.4 The error ε caused by the perturbation of kpT 图5 kiT 2的微小摄动引起的极点相对误差的验证结果Fig.5 The error ε caused by the perturbation of kiT 2 为验证变量小数字长模型,将表3确定的各变量的小数字长带入式(13)中,得到各变量进行量化操作时所存在的误差方差值,然后据此产生相应的白噪声信号,输入给所设计的锁相环中的相应误差源端,采集锁相环的输出信号,分别求取方差值,与设定的准确度指标ζ比较,若小于ζ,则证明所提模型正确。图6分别给出了误差e1、e4、e5、e6、e7、e8对输出的影响曲线。设定准确度曲面是模型中所给定的准确度指标ζ,本文取ζ=1×10-3,可见,按照表3所选取小数字长表示各变量时,所存在的量化误差对锁相环输出的影响都控制在设置准确度之内,从而保证锁相环在全数字硬件化实现时变量表示准确度满足要求。 图6 变量小数字长验证结果Fig.6 The fraction word-lengths of state variables 3.3 实验验证分析 本文建立了锁相环的整数字长和小数字长模型,其中整数字长模型主要是保证设计不出现上溢错误,小数字长模型主要是将有限字长效应控制在设定范围内。 对于整数字长验证,设计如下验证思路:首先,依据所提模型,设定ε=0.006 7,ζ=1×10-3,求得内部信号的表示字长,用FPGA实现,然后,遍历所有输入取值,记录对应的内部所有信号值,其都在所选整数字长可表示的范围内,说明信号不会发生向上溢出,证明了整数字长模型的正确性,由于数据过多,限于篇幅,在此不予给出。 对于小数字长模型的验证,设计如下验证思路:选定一组kpT和kiT2值,则此时系数量化误差将不对系统输出误差产生影响,输出误差主要来自变量的量化误差,从而得到变量小数字长模型验证结果如图7所示。图中的CH4误差信号为理想模型的输出值与实际模型输出值之差经过数模转换后的电压值,其中,理想模型为定点实现时,内部算法不进行截断操作的锁相环,实际模型即为按照ε=0.006 7,ζ=1×10-3所进行设计的锁相环,两者之差即可认为是实际模型输出受有限字长影响而产生的误差。数字1对应为模拟量的5 V,排除干扰毛刺影响后,输出误差的峰值为20 mV,误差准确度为4×10-3,再考虑数模转换时的误差,基本可验证本文的变量小数字长模型的正确性。 图7 实验结果Fig.7 The experimental result of QPLL 本文提出一种基于FPGA/ASIC的全数字硬件化锁相环的建模方法,通过建立锁相环的整数字长和小数字长模型,为锁相环的全数字硬件化设计提供理论依据。得到如下结论: 1)分别利用稳定性判据和卷积确定了系数和变量的动态范围,利用系统灵敏度理论和L2范数确定了系数和变量的稳态准确度,从而得到锁相环的整数和小数字长模型。 2)上述模型中的可配置参数为系数准确度指标ε和变量准确度指标ζ,通过设置两个准确度指标,可得到相对应的内部各信号的表示字长,从而使基于FPGA/ASIC的全数字硬件化正交锁相环的实现变得非常简单。 3)上述设计方法可推广到全数字硬件化闭环算法的实现中,具有重要的应用价值。 [1] 刘亚静,范瑜.全数字伺服电机轴角转换单元建模与分析[J].中国电机工程学报,2013,33(3):148-154. Liu Yajing,Fan Yu.Modeling and analysis of an all-digital magnetic encoder-to-digital converter for servo motors[J].Proceedings of the CSEE,2013,33(3):148-154. [2] 刘亚静,范瑜.离散周期对伺服系统用全数字硬件化锁相环的影响机理分析[J].电工技术学报,2014,29 (9):153-160. Liu Yajing,Fan Yu.Effect of discrete period on all-digital full-hardware phased locked loop using in servo system[J].Transactions of China Electrotechnical Society,2014,29(9):153-160. [3] 刘亚静.多轴电机控制的集成技术研究[D].哈尔滨:哈尔滨工业大学,2011. [4] Cmar R,Rijinders L,Schaumont P.A methodology and design environment for DSP ASIC fixed point refinement[C].Proceedings of automation and test in europe conference,Munich,Germany,1999:271-276. [5] Fang C F,Rutenbar R,Chen T.Fast,accurate static analysis for fixed-point finite-precision effects in DSP design[C].International conference on computer-aided design,San Jose,CA,2003:275-282. [6] Ozer E,Nisbet P,Gregg D.A stochasitic bitwidth estimation technique for compact and low-power custom processors[J].ACM Transactions on Embedded Computing Sysetm,2008,7(3):1-30. [7] Williamson D,Kadiman K.Optimal finite wordlength linear quadratic regulation[J].IEEE Transactions on Automatic Control,1989,34(12):1218-1228. [8] Wu J,Chen S,Li G,et al.An improved closed-loop stability related measure for finite-precision digital controller realizations[J].IEEE Transactions on Automatic Control,2001,46(7):1162-1166. [9] Li G,Gevers M.Optimal finite precision implement- ation of a state-estimate feedback controller[J].IEEE Transactions on Circuits and Systems,1990,37(12):1487-1498. [10]Cheng K Y,Tzou Y Y.Design of a sensorless commu- tation IC for BLDC motors[J].IEEE Transactions on Power Electronics,2003,18(6):1365-1375. [11]周兆勇,李铁才,高桥敏男.基于矢量控制的高性能交流电机速度伺服控制器的FPGA实现[J].中国电机工程学报,2004,24(5):168-173. Zhou Zhaoyong,Li Tiecai,Toshio Takahashi.FPGA implementation of the high-performance vector- controlled speed servo controller of AC drivers[J].Proceedings of the CSEE,2004,24(5):168-173. [12]Jung S L,Chang M Y,Jyang J Y.Design and implementation of an FPGA-based control IC for AC-voltage regulation[J].IEEE Transactions on Power Electronics,1999,14(3):522-532. [13]Naouar M W,Naassani A A,Monmasson E.FPGA-based predictive current controller for synchronous machine speed drive[J].IEEE Transactions on Power Electronics,2008,23(4):2115-2126. [14]Naouar M W,Monmasson E,Naassani A A.FPGA-based current controllers for AC machine drives—a review[J].IEEE Transactions on Industrial Electronics,2007,54(4):1907-1925. [15]Monmasson E,Cirstea M N.FPGA design methodology for industrial control systems—a review[J].IEEE Transactions on Industrial Electronics,2007,54(4):1824-1842. Modeling and Analysis of All-digital Full-hardware Quadrature Phase-locked Loop LiuYajingFanYu (School of Electrical Engineering Beijing Jiaotong University Beijing 100044 China) The word-length modeling method for all-digital full-hardware (ADFH) quadrature phase-locked loop (QPLL) that is implemented with field programmable gate array (FPGA) or application specific integrated circuits (ASICs) is proposed for word-length optimization brought by full-customized FPGA/ASIC. The integer word-length model of the coefficients and the internal variables are built using stability criterion and convolution respectively. Then,the coefficient and internal variable fraction word-length model are constructed in accordance with the system sensitivity theory and norm2 separately. So the ADFH QPLL can be designed using the proposed method with predefined coefficient precision parameterεand variable precision parameterζ. The method can effectively avoid overflow errors and finite-word-length effect with minimum cost. Simulation and experiment results verify the validity of the proposed model. Quadrature phase-locked loop (QPLL),all-digital full-hardware (ADFH),word-length model,finite-word-length effect 国家自然科学基金(51407005,51377009),高等学校博士学科点专项科研基金(20130009120032)和中央高校基本科研业务费(2013JBM084)资助。 2014-12-11 改稿日期2015-05-25 TM315 刘亚静 男,1981年生,博士,讲师,研究方向为电机数字控制系统集成化设计,伺服系统,运动控制IP核等。(通信作者) 范 瑜 男,1954年生,教授,博士生导师,研究方向为磁悬浮与特种电机及其控制。
2 全数字硬件化锁相环建模


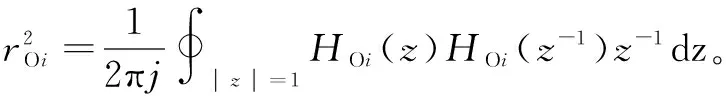

3 实验结果分析
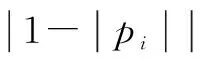








4 结论

