基于功率灵敏度的线路过载划区域紧急控制策略

徐 岩 郅 静

(新能源电力系统国家重点实验室(华北电力大学) 保定 071003)



基于功率灵敏度的线路过载划区域紧急控制策略

徐 岩 郅 静

(新能源电力系统国家重点实验室(华北电力大学) 保定 071003)

为避免切除因潮流转移导致过载的线路，提出一种基于功率灵敏度的线路过载划区域紧急控制策略。以电流相关度系数矩阵为基础，推导出线路功率变量与节点注入功率变量之间的功率灵敏度矩阵，令平衡机参与到紧急控制中，同时将复杂的矢量运算简化为实数运算。根据电网拓扑结构划分广义潮流转移区域，证明区域外节点和区域连接割点对区域内线路有极其接近的功率灵敏度，使计算范围从全网简化到过载线路所属的广义潮流转移区域。将局部灵敏度计算法和稀疏矢量技术结合，大幅度减少了计算量和内存量。利用综合灵敏度选择控制节点组，采用反向等量调整法，并结合正常线路冗余量约束计算功率调整量，有效避免了潮流校验，提高了紧急控制速度。在IEEE39和IEEE118节点系统中验证了该方法的正确性和优越性。

电力系统 线路过负荷 功率灵敏度 广义潮流转移区域 局部灵敏度计算法

0 引言

电力系统中故障线路切除引起潮流转移，易导致其他线路过载，引起过载保护动作切除线路，导致连锁跳闸，甚至大停电事故[1，2]。当电网中发生潮流转移时，快速准确地判断出某些线路是由于潮流转移导致过负荷后备保护的启动，快速闭锁其后备保护，并采取相应的紧急控制措施消除线路过载，对保证系统的安全运行具有重要意义[3]。

以往多数方法[4-8]中，采取紧急控制措施消除线路过载时，平衡机都不参与调节，这极易导致无法得到最优控制方案。例如，某线路过载，电网中对该线路有最佳减载调节效果的发电机是平衡机，但由于在求取控制方案时不考虑平衡机，因而无法得到最优控制方案。以往方法计算节点对线路潮流的灵敏度时，都采用直流潮流法[4-10]，需依赖于平衡机的选择，令平衡机对所有线路的灵敏度为0[5]，同时，当平衡机不同时，得到的紧急控制方案也可能不同[11]。

在文献[3，12]的紧急控制中，平衡机参与了调节。文献[3]推导了支路电流与节点注入电流之间的电流相关度系数矩阵，该矩阵中相关度系数都是复数，且描述的是电流矢量之间的关系，在计算控制节点需要调整的功率量时，还需要进行功率与电流矢量之间的变换，这涉及到复数与矢量之间的复杂运算。文献[12]利用潮流跟踪算法确定控制节点，该方法计算量较大，且当电网规模较大或因线路断开导致电网拓扑发生变化时，该方法的适用性较差。以上两种方法虽然令平衡机参与紧急控制，但未考虑平衡机在电网运行中需要担负的调频任务[13]及平衡电网微小功率差额的任务[12]，未对平衡机的可调节量进行适当限制。

另外，以往方法在选择控制节点或计算功率调整量时，计算范围涉及全网的所有节点和线路，当电网规模较大时，计算量大，控制速度慢，有可能无法满足紧急控制的时间要求[6]。

本文提出一种基于功率灵敏度的线路过载划区域紧急控制策略。以电流相关度系数矩阵为基础，推导出线路功率变量与节点注入功率变量之间的功率灵敏度矩阵，将复杂的电流矢量运算简化为功率之间的实数运算，同时可得到平衡机对各线路的灵敏度，令平衡机参与到紧急控制中。根据电网拓扑结构划分广义潮流转移区域，证明区域外节点和区域连接割点对区域内线路有极其接近的功率灵敏度，将计算范围从全网简化到过载线路所属的广义潮流转移区域。将局部灵敏度计算法和稀疏矢量技术结合，大幅度减少了计算量和内存量。考虑节点对过载线路和接近极限线路的共同作用，利用综合灵敏度筛选得到控制节点组；采用反向等量调整法，考虑节点可调量、线路过载量及正常线路冗余量确定功率调整量，有效避免了潮流校验，提高了紧急控制速度。

1 基于广义潮流转移区域的功率灵敏度

1.1 电流相关度系数矩阵

高压输电网络中线路的电抗值远大于电阻值，因此分析计算中可用电抗值代替阻抗值[14]。将电网中的发电机、负荷都作为节点注入电流来表示，当不考虑电网中的电力电子等非线性元件时，网络的节点电压方程为

IN=YNUN

(1)

式中：IN为节点注入电流列矢量(以流入节点的方向为正方向)；UN为节点电压列矢量；YN为节点电纳矩阵。

网络支路电流与节点电压之间的关系为

IB=YBATUN

(2)

式中：IB为支路电流列矢量；YB为支路电纳矩阵；A为节点关联矩阵。

根据式(1)和式(2)可得

(3)

由式(3)可知，支路电流和节点注入电流之间为线性关系，定义电网相关度系数矩阵C(λ)为

(4)

对于一个含有n个节点、b条支路的网络，C(λ)是b×n阶实数矩阵，且C(λ)仅与网络参数及拓扑结构有关[3]。以支路k为例，其电流矢量Ik,B是各节点注入电流的线性组合

Ik,B=λk-1I1,N+…+λk-iIi,N+…+λk-nIn,N

(5)

1.2 功率灵敏度矩阵

实际运行中进行紧急控制时，需确定的是能有效消除线路过载的控制节点及其功率调整量，式(3)中描述的是支路电流与节点注入电流之间的关系，需对其进行处理，得到支路功率与节点注入功率之间的关系。对式(5)进行处理得到

(6)

式中：Uk,B为第k条支路的首端电压矢量；Ui,N为第i个节点的电压矢量。将式(6)展开得

(7)

式中：Pk,B和Qk,B分别为支路k的有功功率和无功功率；Pi,N和Qi,N分别为第i个节点的注入有功功率和注入无功功率；Uk,B和φk,B分别为支路k首端电压模值和相角；Ui,N和φi,N分别为第i个节点电压模值和相角。

将式(7)展开，得到实数部分为

(8)

紧急控制中，只调节控制节点的有功，不改变其无功，因此，将式(8)中支路有功功率和节点注入有功功率取变量形式，将节点注入无功功率的变量取为0，可得

(9)

定义矩阵D(β)为支路功率变量与节点注入功率变量之间的功率灵敏度矩阵，其中支路k功率变量与节点i注入功率变量之间的功率灵敏度βk-i为

(10)

1.3 广义潮流转移区域

搜索开断线路的潮流转移危险线路时，对电网进行潮流转移区域划分可有效减少计算量[15，16]。其划分原理是，根据广域测量系统(Wide Area Measurement System，WAMS)得到的电网拓扑结构，可将电力系统抽象成一个无向图G(V，E)，V表示节点集合，E表示线路集合。无向图中，如果任意两点之间都存在路径，该无向图称为连通图[17]。连通无向图中，如果去掉1个节点及与该节点相关联的边，图不再连通，称该节点为图的割点。含有割点的图为可分图，可分图可看作由有限个割点连接起来的各个块组成，图中任何一条回路不可能跨越2个或2个以上的块，即构成一条回路的所有支路一定在同一块中[15]，连通图中的块即对应电网中的潮流转移区域。图1中，点2和点4是割点，它们把电网G分为3个潮流转移区域，各区域包含的节点分别是{1，2}、{2，3，4}和{4，5，6}。

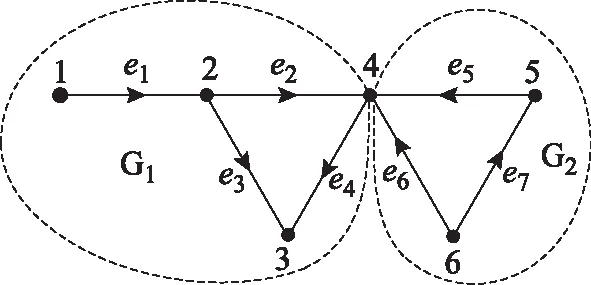
图1 广义潮流转移区域示意图Fig.1 Sketch map of generalized power flow transferring zone

紧急控制中，重点不再是潮流转移路径的搜索，而是确定能够消除线路过载的最佳控制节点和功率调整量，因此需要对潮流转移区域进行扩展得到广义潮流转移区域，扩展原则为：

1)若某节点为邻接节点数目为1的发电机或负荷节点，则将该节点归入其邻接节点所属的广义潮流转移区域中。

2)若某线路断开会导致系统解列为两部分，且这两部分均不是发电机——母线系统，则将这两部分归为不同的广义潮流转移区域。

因此，图1所示的电网结构包括两个广义潮流转移区域，分别是G1和G2，各区域包含的节点分别是{1，2，3，4}和{4，5，6}。

本文利用深度优先搜索方法搜索割点和块来确定广义潮流转移区域。

1.4 基于广义潮流转移区域的电流相关度系数特点

以图1为例，计算支路电流与节点注入电流之间的电流相关度系数矩阵，图中线路的箭头方向为其支路电流方向。

支路电纳矩阵YB=diag[y1，y2，y3，y4，y5，y6，y7]，节点关联矩阵A为

(11)

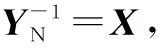
(12)

根据式(4)可计算得到电流相关度系数矩阵C(λ)，见附录中式(A)。根据式(3)可得到支路电流与节点注入电流之间的关系，以支路3为例，其支路电流为

I3,B=λ3-1I1,N+λ3-2I2,N+λ3-3I3,N+
λ3-4I4,N+λ3-5I5,N+λ3-6I6,N

(13)

式中：λ3-1=y3(x21-x31)，λ3-2=y3(x22-x32)，λ3-3=y3(x23-x33)，λ3-4=y3(x24-x34)，λ3-5=y3(x25-x35)，λ3-6=y3(x26-x36)。

利用电抗值代替阻抗值分析计算时，节点电抗矩阵X中元素的物理意义是：自电抗xii表示电网中只有节点i有单位注入电流，其他节点都没有注入电流时节点i的电压；互电抗xij表示电网中只有节点j有单位注入电流，其他节点都没有注入电流时节点i(i≠j)的电压[13]。

节点4注入电流对支路3电流的相关度为λ3-4=y3(x24-x34)，其中(x24-x34)表示当电网中只有节点4有单位注入电流，其他节点都没有注入电流时，节点2与节点3的电压差。节点5注入电流对支路3电流的相关度为λ3-5=y3(x25-x35)，其中(x25-x35)表示电网中只有节点5有单位注入电流，其他节点都没有注入电流时，节点2与节点3的电压差。

观察图1，节点4是割点，因此当电网中只有节点5有单位注入电流，其他节点都没有注入电流时，在不考虑线路损耗的情况下，对于支路3上的电流，其效果与只在节点4有单位注入电流，其他节点都没有注入电流时相同，因此λ3-4=λ3-5。利用以上分析过程可知，在不考虑线路损耗的情况下，对于广义潮流转移区域G1中任一条线路，区域G2中的所有节点与节点4具有相同的电流相关度。

实际电网中，考虑到线路损耗的存在，对于广义潮流转移区域中任一条线路，区域外节点和区域连接割点对区域内线路有极其接近的电流相关度。

1.5 基于广义潮流转移区域的功率灵敏度特点

以图1为例进行说明，由1.4节可知对于支路3，节点4和节点5的电流关联度相同，令λ3-4=λ3-5=λ，其功率灵敏度分别为

(14)

(15)

将式(14)和式(15)作差得

(16)

式(16)中U4，N与U5，N相差不大，且cosφ3,B(cosφ4,N-cosφ5,N)+sinφ3,B(sinφ4,N-sinφ5,N) 很小，因此，β3-4-β3-5≈0，即对于支路3，节点4和节点5的功率灵敏度十分接近。因此，对于广义潮流转移区域G1中任一条线路，区域G2中的所有节点与节点4具有极其接近的功率灵敏度。

综上所述，对于广义潮流转移区域内线路，区域外节点和区域连接割点的功率灵敏度十分接近。制定紧急控制策略时，基于广义潮流转移区域的功率灵敏度有很大优势，体现在如下几方面：

1)选择控制节点时，只需计算过载线路所属的广义潮流转移区域中各节点的综合灵敏度(见2.1.1节)，其他区域中节点的功率灵敏度与相应割点的功率灵敏度十分接近。

2)考虑正常支路冗余量对功率调整量的约束时，只需计算控制节点组对过载线路及控制节点所在的广义潮流转移区域中正常线路的功率灵敏度(见2.2节)。

3)功率灵敏度矩阵描述的是支路功率变量与节点注入功率变量之间的线性关系，将文献[3]中电流之间的矢量计算简化为功率之间的实数运算，简化了计算过程。

4)功率灵敏度的计算不依赖于平衡机的选择，且能准确计算出平衡机对各线路的功率灵敏度，令平衡机参与到紧急控制中。

5)当电网因线路断开导致拓扑结构发生变化时，根据WAMS提供的实测信息对YB、A和YN进行局部修正，并结合电压量通过简单计算即可得到功率灵敏度矩阵，和文献[12]中方法相比，计算量大大减少。

2 紧急控制策略

支路最大传输功率既受到热稳定功率极限的限制，也受到其后备保护整定值所对应的最小传输功率的限制，应将支路最大允许传输功率取为上述二者中的最小值[18]。本文将支路热稳定功率极限作为其最大传输功率，实际电网运行中依情况而定。

制定防止线路连锁过载跳闸的紧急控制策略主要包括两方面：①控制节点的选择；②功率调整量的计算。

2.1 控制节点的选择

2.1.1 综合灵敏度

根据式(9)可知，为了使系统的功率调整量最少，应优先调节对过载线路功率灵敏度较大的节点，同时应保证不出现新的线路过载。以往多数方法仅依据对过载线路的灵敏度选择控制节点[4，5，9]，这时如果所选的控制节点对过载线路和接近极限线路(如大于线路热稳定极限的90%[19])的作用相反，可能会造成更加严重的过载情况。本文根据节点i对过载线路和接近极限线路的控制作用定义其综合灵敏度为

(17)

式中：fL-i为节点i的综合灵敏度；L为过载线路及接近极限线路集合；αk为线路k的过载率，对于过载线路αk>1，对于接近极限线路0.9<αk<1，线路过载程度越大，其在综合灵敏度计算公式中的重要性权重越大。综合灵敏度充分考虑了节点对过载线路及接近极限线路的综合控制作用，避免了调整过程中接近极限线路功率增加导致新的线路过载。

2.1.2 控制节点组

计算过载线路所属的广义潮流转移区域中各节点的综合灵敏度，将该区域中的边界割点看作发电机，对节点进行分类处理：

1)若f(i)>0且节点i为可调发电机，说明减少该节点的发电机出力可以降低过载线路和接近极限线路的整体过载程度，将该节点归入减出力节点集合Jm。

2)若f(j)<0且节点j为可调发电机或可切负荷，说明增加该节点的发电机出力或减少该节点的负荷可降低过载线路和接近极限线路的整体过载程度，将该节点归入加出力节点集合Jp。

将Jm中节点按照综合灵敏度从大到小进行排序，将Jp中节点按照综合灵敏度从小到大进行排序，同时，为了尽量避免切除负荷，采取发电机优先调节原则，即将Jp中的发电机节点排在所有负荷节点之前。排序时，将割点看作发电机节点，且当两个同类型节点(两个发电机节点或者两个负荷节点)拥有相同的灵敏度时，按照可调量降序排列。

为了保证系统功率平衡，本文采用反向等量配对调整法[5]：为每个减出力节点都找到一个与之配对的加出力节点，同时，每个控制节点组的加减出力调整量相等。

按节点排序分别从Jm和Jp中选择一个减出力节点A和加出力节点B，利用2.2节中方法得到的调整量进行调整，利用WAMS测量的调整后系统中的支路功率判断过载是否消除，若已消除，则紧急控制结束；若过载依旧存在，则A或者B中有不再可调节点，则从不再可调节点所属的集合中按顺序选择下一节点，继续进行下一轮调整，直至过载消除。

上述过程中，有以下两点需要说明：

1)式(10)计算功率灵敏度所需要的物理量中，λk-i只与电网拓扑结构有关，而电压模值、相角与系统的运行状态有关，考虑到调整前后系统的节点电压变化很小[3]，为了节省紧急控制时间，每一轮调整后，不再重新计算各节点的功率灵敏度。

2)当割点被选作减出力节点(或加出力节点)时，计算与该割点相连接的其他广义潮流转移区域中各节点的综合灵敏度，并将这些节点加入到Jm(或Jp)中进行排序，按照排序选择控制节点，并用该控制节点代替A(或B)。

2.2 功率调整量的计算

根据反向等量配对调整法，每个控制节点组中减出力节点i和加出力节点j的调整量都相等，其调整目标是在控制节点i和j的可调量范围内，消除过载线路的过载量，同时保证没有新线路过载。

当减出力节点i和加出力节点j配对调整时，对于任一条线路k，其控制节点组的功率灵敏度是ηk-(i-j)=βk-i-βk-j，当ηk-(i-j)>0时，表示控制节点组i-j会使线路k功率减少；当ηk-(i-j)<0时，表示调整i-j会使线路k功率增加。

对于过载线路集合M中任一条过载线路m，设其功率为Pm，热稳定功率极限为Pmmax，考虑到灵敏度及调整量计算误差等因素，定义可靠系数ξ<1，要消除线路m过载，控制节点组i-j需要调整的功率量为

ΔPm-(i-j)=(Pm-ξPmmax)/ηm-(i-j)

(18)

本文取ξ=0.95，实际电网中根据情况适当取值。

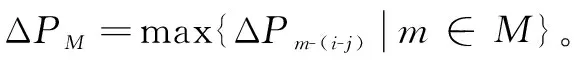
为避免紧急控制过程中出现新的支路过载，要考虑控制节点组i-j对正常线路(包括接近极限线路)的控制作用。对于正常线路集合N中任一条线路n，若ηn-(i-j)<0，说明控制节点组i-j会使正常线路n的潮流增加，将线路n归入潮流增加线路集合Z，并根据其功率冗余量对i-j的调整量进行限制，即调整量不能超过

ΔPn-(i-j)=(Pn-Pnmax)/ηn-(i-j)

(19)

综上所述，控制节点组i-j的最终调整量为

ΔPij=min{ΔPM, ΔPZ, ΔPi, ΔPj}

(20)

需要注意：

1)若加出力节点j是平衡机，考虑到平衡机需要担负调频等任务，在计算其可调量时，预留一定裕度，可调量计算公式为

ΔPj=Pjmax-Py-Pj

(21)

式中：Pjmax为平衡机的最大发电量；Py为平衡机预留裕度；Pj为平衡机目前的发电量。本文取Py=10 MW，实际电网运行中可根据情况适当取值。

2)正常线路集合N是过载线路和控制节点所在的广义潮流转移区域中所有正常线路的并集。

3)每一轮调整后，修正控制节点组的可调量，并利用WAMS刷新电网所有支路功率，判断线路过载是否消除，若需要继续进行下一轮紧急控制，则根据刷新后的新一轮控制节点组可调量及支路功率计算新一轮调整量。

2.3 局部灵敏度计算法

利用本文方法制定紧急控制策略时，不需要计算全网所有节点与所有线路之间的功率灵敏度，只需计算部分节点对部分线路的功率灵敏度，即局部灵敏度计算法：在选取控制节点时，只需计算过载线路所属的广义潮流转移区域中各节点对过载线路及接近极限线路的灵敏度；在考虑正常支路冗余量对功率调整量的约束时，只需计算控制节点组对过载线路及控制节点所在的广义潮流转移区域中正常线路的功率灵敏度。

观察矩阵YB、A、X及附录中的C(λ)，计算所有节点对某支路k的电流灵敏度时，只需保留AT中的第k行元素，其他元素均可置0；计算某节点i对所有支路的电流灵敏度时，只需保留X中的第i列元素，其他元素均可置0。利用以上方法可方便求得电网中部分节点与部分线路之间的电流灵敏度，进而得到功率灵敏度。

同时，在采用局部灵敏度计算法时，矩阵中大部分元素为0，利用稀疏矢量技术可极大地提高计算速度和减少内存量。

3 紧急控制步骤及流程图

当潮流转移导致某些线路过载时，立即闭锁其过载后备保护并采取紧急控制措施消除过载。紧急控制步骤总结如下：

1)计算过载线路所属的广义潮流转移区域中各节点的综合灵敏度，根据综合灵敏度将节点分为减出力节点集合Jm和加出力节点集合Jp，并对集合中节点排序，按顺序分别从两个集合中选择减出力节点A和加出力节点B，构成控制节点组A-B。

2)若A(或B)为割点，则计算与该割点相连接的其他广义潮流转移区域中各节点的综合灵敏度，并将这些节点加入到Jm(或Jp)中进行排序，按照排序选择控制节点，并用选中的控制节点D代替A(或B)，构成控制节点组D-B(或A-D)。为描述方便，以下步骤中，将控制节点组统一称为i-j。

3)利用2.2节中方法计算控制节点组i-j的调整量ΔPij。

4)根据节点i减出力ΔPij、节点j加出力ΔPij(或切负荷ΔPij)，对控制节点的可调量进行修正，利用WAMS测量并刷新调整后系统中的支路功率，判断过载是否消除，若是，则紧急控制结束；若过载依旧存在，则i或j中有不再可调节点，则从不再可调节点所属的集合中按顺序选择下一节点，构成新的控制节点组。重复步骤2)～步骤4)直至过载消除。

紧急控制流程图如图2所示。

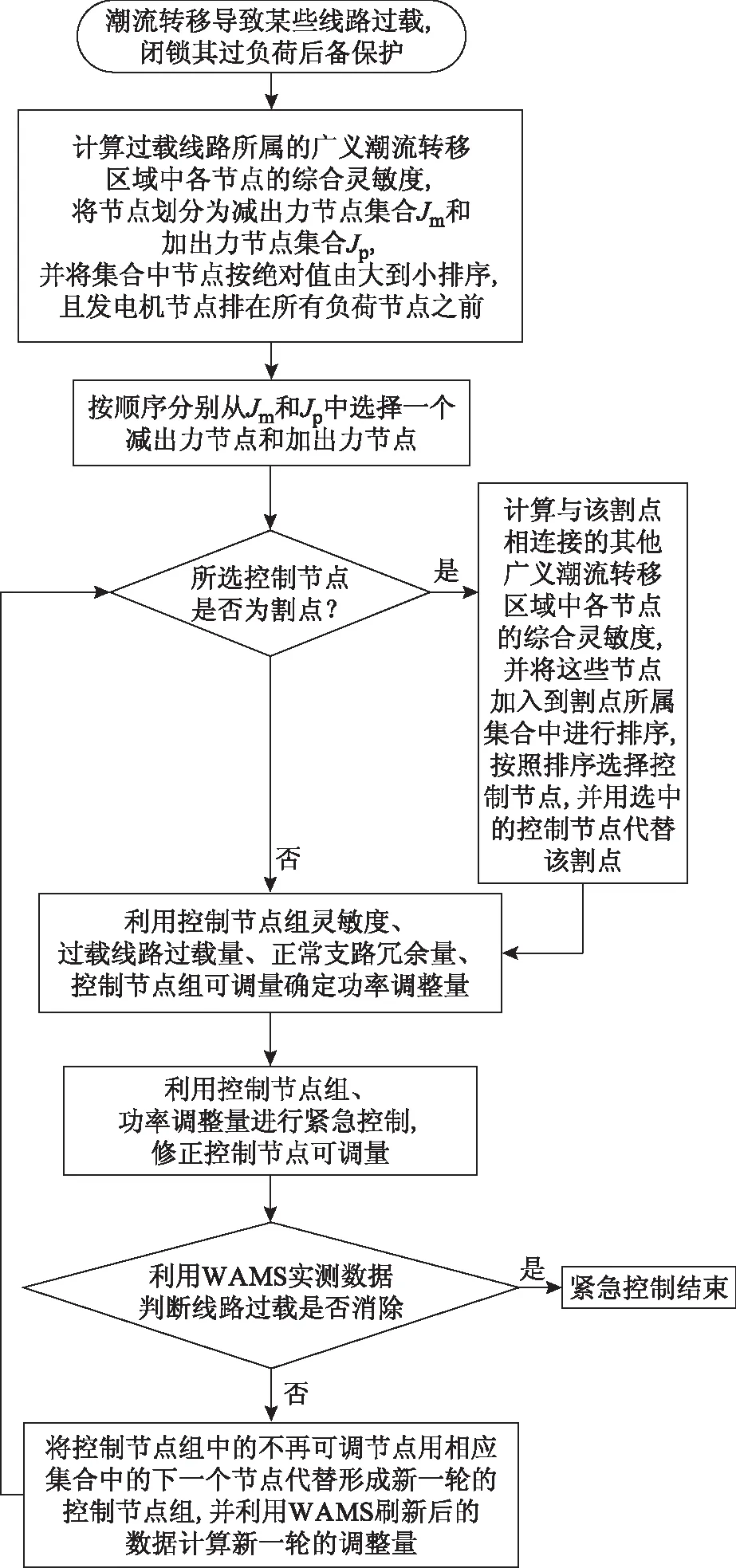
图2 紧急控制算法流程图Fig.2 Flow chart of the emergency control algorithm

4 仿真算例

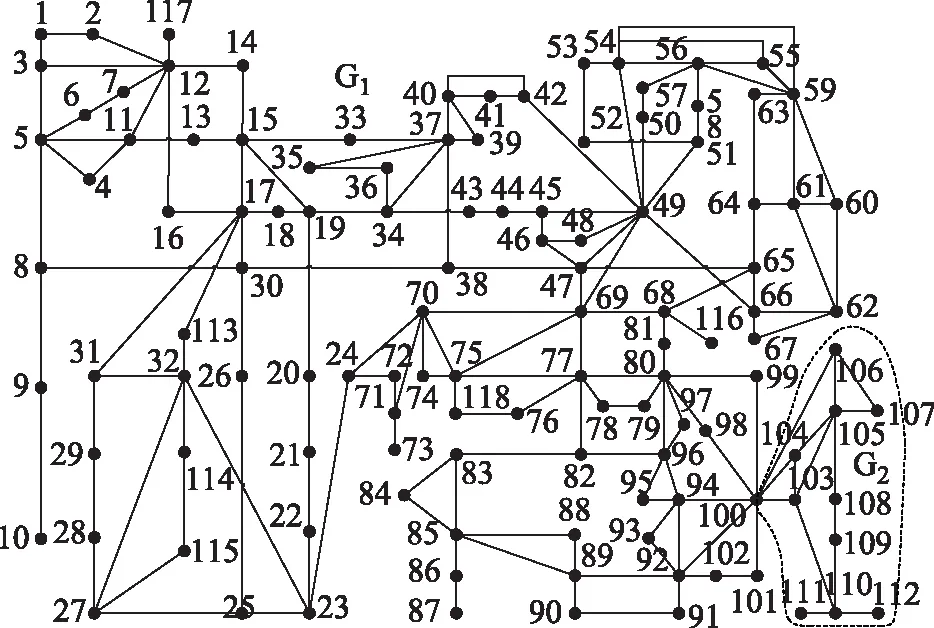
利用PSASP软件在IEEE39和IEEE118节点系统中对本文方法进行验证。IEEE39节点系统包括4个广义潮流转移区域，分别是G1、G2、G3和G4，如图3所示。IEEE118节点系统包括2个广义潮流转移区域，分别是G1和G2，如附录中图B所示，因IEEE118节点系统规模较大，附录中图B未显示出发电机及负荷标志，IEEE118节点系统的详细示意图见文献[20，21]。IEEE39节点系统中节点31是平衡机，IEEE118节点系统中节点69是平衡机，本文仿真中在计算平衡机节点出力可增量时均已留出10 MW的裕度量。

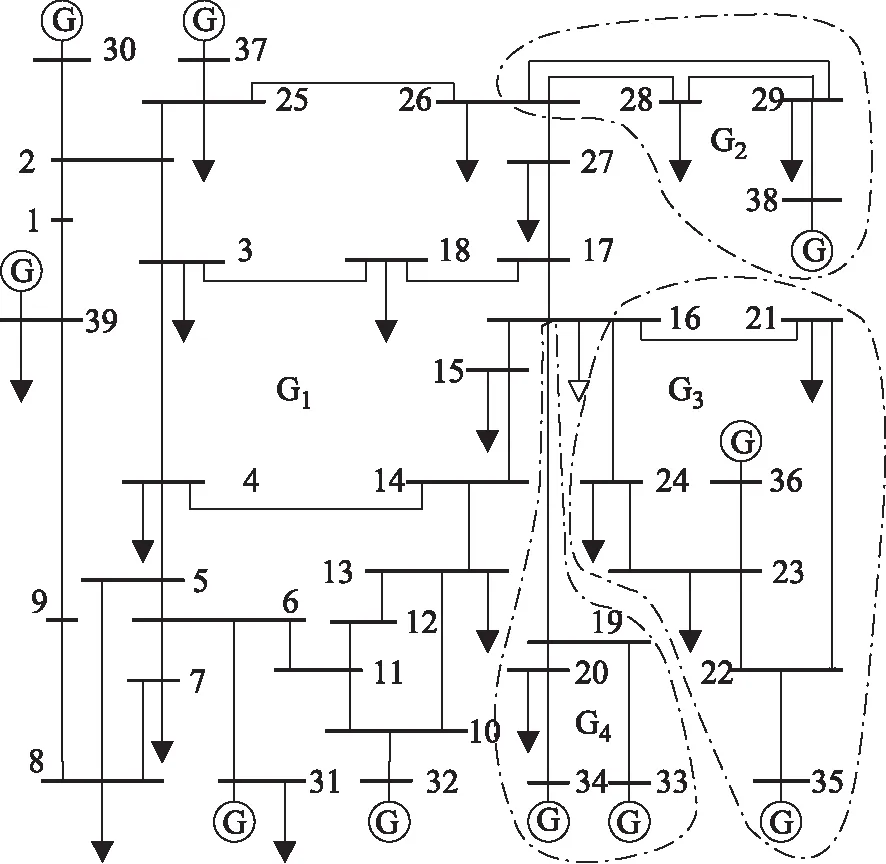
图3 IEEE39节点系统Fig.3 IEEE39 bus system

4.1 仿真一

IEEE39节点系统中，线路11-6因故障断开，导致线路10-13、13-14和14-4过载，无接近功率极限线路，此时过载线路功率如表1所示。

表1 IEEE39节点系统线路11-6断开时过载线路功率Tab.1 Power of overload lines with line 11-6 removal in IEEE39 bus system

开断线路和过载线路均位于广义潮流转移区域G1中，计算该区域中各节点的综合灵敏度，并对节点进行分类排序形成减出力节点集合Jm和加出力节点集合Jp。因篇幅有限，列出每个集合中的前3个节点，如表2所示。

表2 仿真一的Jm和JpTab.2 Jm and Jp of simulation 1

按节点排序分别从Jm和Jp中选择减出力节点32和加出力节点31，计算控制节点组32-31对区域G1内所有正常线路的灵敏度，根据2.2节所述方法计算得到调整量为58.08 MW，调整后线路10-13、13-14 和14- 4的功率分别为561.9 MW、582.09 MW和497.36 MW，均在热稳定功率极限范围内。

仿真分析：

本文方法可计算平衡节点31对过载线路的灵敏度，并在仿真一中，平衡节点31是最佳加出力节点，利用控制节点组32-31进行一轮调整即可消除线路过载，调整量为58.08 MW。若利用文献[4，5，7]中方法，平衡机不参与紧急控制，采用直流潮流法计算灵敏度，得到控制节点组为32-39，该节点组对线路10-13、13-14和14- 4的灵敏度分别为0.960、1.008和0.741，一轮调整即可消除线路过载，但需要调整功率93.85 MW。

4.2 仿真二

IEEE39节点系统中，线路2-1和26-27因故障同时断开时，会导致线路2-3和25-2过载，无接近极限线路。此时过载线路功率如表3所示。

表3 IEEE39节点系统线路2-1和26-27断开时过载线路功率Tab.3 Power of overload lines with line 2-1 and 26-27 removal in IEEE39 bus system

开断线路和过载线路均位于区域G1中，计算该区域中各节点的综合灵敏度，并对节点进行分类排序形成减出力节点集合Jm和加出力节点集合Jp。集合中部分节点如表4所示。

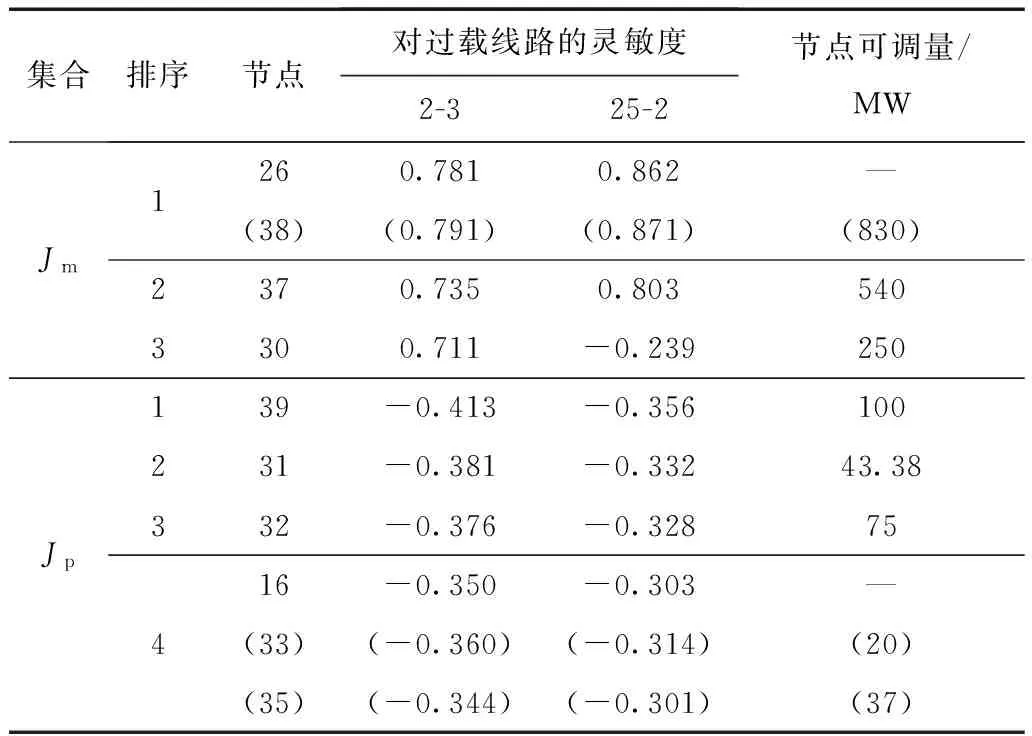
表4 仿真二的Jm和JpTab.4 Jm and Jp of simulation 2

按节点排序从Jm和Jp中选中最佳减、加出力节点分别为26和39，节点26为割点，通过该割点与G1相连接的广义潮流转移区域是G2，因割点26为减出力节点，所以只需计算G2中发电机节点的综合灵敏度，并将其按灵敏度排序插入到Jm中，按顺序代替节点26作为控制节点。区域G2中只有节点38为发电机节点，用38代替26，得到控制节点组38-39，计算该控制节点组对G1和G2内所有正常支路的灵敏度，并根据2.2节所述方法计算得到调整量为100 MW，调整后线路2-3依旧过载，而节点39已不可调。

按顺序从Jp中选择31为加出力节点，构成第二轮控制节点组38-31，计算得到功率调整量为43.38 MW，调整后线路2-3依旧过载，而节点31已不可调。按顺序从Jp中选择32为加出力节点，构成第三轮控制节点组38-32，计算得到调整量为75 MW，调整后线路2-3依旧过载，而节点32已不可调。按顺序从Jp中选择16为加出力节点，但节点16为割点，通过该割点与G1相连接的广义潮流转移区域是G3和G4，计算G3和G4中各节点的综合灵敏度，并将其按灵敏度排序插入到Jp中，且发电机节点排在所有负荷节点之前，按顺序代替节点16作为控制节点。得到第四轮控制节点组38-33，计算得到调整量为20 MW，调整后线路2-3依旧过载，而节点33已不可调。按顺序从Jp中选择35为加出力节点，构成第五轮控制节点组38-35，计算得到调整量为37 MW，线路过载消除，紧急控制结束。各轮紧急控制如表5所示。

表5 仿真二紧急控制策略Tab.5 The emergency control strategy of simulation 2

仿真分析：

1)割点26为减出力节点，说明区域G2中各节点的综合灵敏度均为正值，因此只需计算G2中发电机节点的综合灵敏度，并将其按灵敏度排序插入到Jm中，依次代替节点26作为控制节点。

2)节点34的综合灵敏度比节点35的综合灵敏度小，但节点34已是最大发电出力，即出力可增量为0，因此该节点不属于Jp。

4.3 仿真三

IEEE118节点系统是国际通用仿真系统，但该系统参数中不含支路热稳定功率极限及各发电机发电上限等参数，同时该系统中部分发电机的发电量为0，且各线路传输的功率量都较小[20，21]。本文规定该系统支路热稳定功率极限如附表1所示，同时，规定系统中各发电机的出力可增量均为25 MW。虽然IEEE118节点系统中支路热稳定功率极限及各发电机出力可增量由本文人为设定，但不影响在该系统中对本文方法可靠性和优越性的验证。

IEEE118节点系统中，线路103-110因故障断开，导致线路103-105和105-108过载，无接近功率极限线路，此时过载线路功率如表6所示。

表6 IEEE118节点系统线路103-110断开时过载线路功率Tab.6 Power of overload lines with line 103-110 removal in IEEE118 bus system

开断线路和过载线路均位于区域G2中，计算该区域中各节点的综合灵敏度，并对节点进行分类排序形成减出力节点集合Jm和加出力节点集合Jp。集合中部分节点如表7所示。

表7 仿真三的Jm和JpTab.7 Jm and Jp of simulation 3

按节点排序从Jm和Jp中选中最佳减、加出力节点分别为103和110，计算控制节点组103-110对区域G2内所有正常线路的灵敏度，根据2.2节所述方法计算得到功率调整量为25 MW，调整后线路103-105和105-108的功率分别为57.49 MW和60.20 MW，均在热稳定功率极限范围内。

仿真分析：

1)仿真三中，利用式(18)分别计算为使线路103-105和105-108消除过载时控制节点组103-110需要调整的功率量，计算结果为29.54 MW和12.398 MW，但本算例中节点110的出力可增量为25 MW，因此功率调整量最终确定为25 MW。式(18)中ξ=0.95，即利用控制节点组103-110将线路103-105的功率由68.52 MW降为0.95×60 MW时需要的调整量是29.54 MW，当调整量为25 MW时，线路103-105的功率降为57.49 MW，满足消除过载的要求。可靠系数ξ<1，其作用是防止计算误差导致所选的调整量不满足消除过载的要求，实际运行中根据情况适当取值。

2)仿真一、二、三中均未出现接近极限线路，但同时考虑控制节点对过载线路和接近极限线路作用的综合灵敏度的优势在文献[19]中已显著体现。

3)计算量分析：在IEEE39节点系统进行的仿真中，仿真一只需计算区域G1中各节点对过载线路及接近极限线路(共3条)的灵敏度，且只需计算控制节点组(共2个节点)对G1中正常线路的灵敏度，G1中节点数目占全网的66.7%，线路数目占全网的67.4%；仿真二在选取控制节点组时虽然需要计算全网节点对过载线路及接近极限线路(共2条)的灵敏度，但在每一轮的紧急控制中只需计算控制节点组(每一轮紧急控制中控制节点数为2)对电网部分区域中正常线路的灵敏度。在IEEE118节点系统进行的仿真中，仿真三只需计算区域G2中各节点对过载线路及接近极限线路(共2条)的灵敏度，且只需计算控制节点组(共2个节点)对G2中正常线路的灵敏度，G2中节点数目占全网的9.3%，线路数目占全网的8.1%。因此，通过划分广义潮流转移区域，使紧急控制计算涉及到的节点数目及线路数目大量减少。

本文方法只需计算电网中部分节点对部分线路的功率灵敏度，利用2.3节中所述的局部灵敏度计算法及稀疏矢量技术可大幅度减少计算量及内存量，同时，该方法在计算调整量时考虑了正常支路冗余量，有效避免了潮流校验，计算过程快速有效，提高了紧急控制速度。

文献[4，7]在选取控制节点及考虑正常支路冗余量对功率调整量的约束时，计算范围涉及全网所有节点及线路；文献[8，19]利用优化规划算法求解紧急控制方案，迭代次数较多；文献[12]利用潮流跟踪算法计算每台发电机、每个负荷对各条线路的占用率，然后按比例切机、切负荷以消除线路过载，计算过程复杂。以上方法运算量大，计算时间较长，本文方法计算范围只涉及电网中部分节点和线路，同时，局部灵敏度计算法及稀疏矢量技术的应用使得计算量大幅度减少，提高了紧急控制速度，满足在线应用的要求。

5 结论

本文提出一种基于功率灵敏度的线路过载划区域紧急控制策略。该方法的主要特点为：

1)以电流相关度系数矩阵为基础，推导出线路功率变量与节点注入功率变量之间的功率灵敏度矩阵，可计算出平衡机对各线路的灵敏度，令平衡机参与到紧急控制中，同时，将电流之间复杂的矢量运算简化为功率之间的实数运算。

2)根据电网拓扑结构划分广义潮流转移区域，证明区域外节点和区域连接割点对区域内线路有极其接近的功率灵敏度，从而将计算范围从全网简化到过载线路所属的广义潮流转移区域。

3)采用局部灵敏度计算法，只需计算电网中部分节点对部分线路的功率灵敏度。将局部灵敏度计算法和稀疏矢量技术结合，大幅度减少了计算量和内存量。

4)利用综合灵敏度选择控制节点，采用反向等量调整法，并结合正常线路冗余量确定功率调整量，有效避免了潮流校验，提高了紧急控制速度。

[1] 杨文辉，毕天姝，马强，等.基于广域电压相角信息的输电断面快速识别方法[J].电力系统保护与控制，2013，41(24)：58-63. Yang Wenhui，Bi Tianshu，Ma Qiang，et al.A method for searching transmission section based on wide-area voltage phasors[J].Power System Protection and Control，2013，41(24)：58-63.

[2] 王增平，李刚，任建文.基于前K最短路径的输电断面搜索新算法[J].电工技术学报，2012，27(4)：193-201. Wang Zengping，Li Gang，Ren Jianwen.A new search algorithm for transmission section based on K shortest paths[J].Transactions of China Electrotechnical Society，2012，27(4)：193-201.

[3] 徐慧明，毕天妹，黄少锋，等.基于广域同步测量系统的预防连锁跳闸控制策略[J].中国电机工程学报，2007，27(19)：32-38. Xu Huiming，Bi Tianshu，Huang Shaofeng，et al.Study on wide area measurement system based control strategy to prevent cascading trips[J].Proceedings of the CSEE，2007，27(19)：32-38.

[4] 程临燕，张保会，郝治国，等.基于综合灵敏度分析的快速控制算法研究[J].电力自动化设备，2009，29(4)：46-49. Cheng Linyan，Zhang Baohui，Hao Zhiguo，et al.Fast control algorithm based on integrative sensitivity analysis[J].Electric Power Automation Equipment，2009，29(4)：46-49.

[5] 邓佑满，黎辉，张伯明，等.电力系统有功安全校正策略的反向等量配对调整法[J].电力系统自动化，1999，23(18)：5-8. Deng Youman，Li Hui，Zhang Boming，et al.Adjustment of equal and opposite quantities in pairs for strategy of active power security correction of power systems[J].Automation of Electric Power Systems，1999，23(18)：5-8.

[6] 李刚，王增平，任建文，等.基于图论分区与改进 BFS算法搜索安全约束集的防联锁过载控制策略[J].电工技术学报，2012，27(11)：219-229. Li Gang，Wang Zengping，Ren Jianwen，et al.A control strategy to prevent cascading overload with security constraint set searched by graph theory partition and improved BFS algorithm[J].Transactions of China Electrotechnical Society，2012，27(11)：219-229.

[7] 姚峰，张保会，周德才，等.输电断面有功安全性保护及其快速算法[J].中国电机工程学报，2006，26(13)：31-36. Yao Feng，Zhang Baohui，Zhou Decai，et al.Active power security protection of transmission section and its fast algorithm[J].Proceedings of the CSEE，2006，26(13)：31-36.

[8] 姜臻，苗世洪，刘沛，等.一种基于粒子群优化算法的转移潮流控制策略[J].电力系统自动化，2010，34(18)：16-20，31. Jiang Zhen，Miao Shihong，Liu Pei，et al.A particle swarm optimization based power flow transferring control strategy[J].Automation of Electric Power Systems，2010，34(18)：16-20，31.

[9] 袁晓丹，张会强.多支路开断潮流转移识别及防连锁过载策略研究[J].现代电力，2014，31(5)：74-79. Yuan Xiaodan，Zhang Huiqiang.Study on power flow transferring identification of multi-line tripping and the strategy to prevent cascading overload strategy[J].Modern Electric Power，2014，31(5)：74-79.

[10]吴际舜.电力系统静态安全分析[M].上海：上海交通大学出版社，1985.

[11]沈瑜，夏清，康重庆.发电联合转移分布因子及快速静态安全校核算法[J].电力系统自动化，2003，27(18)：13-17. Shen Yu，Xia Qing，Kang Chongqing.Generation jointly shift distribution factor (GJSDF) and fast security analysis algorithm in economic dispatch[J].Automation of Electric Power Systems，2003，27(18)：13-17.

[12]任建文，李莎，严敏敏，等.基于潮流跟踪算法的线路过负荷紧急控制策略[J].电网技术，2013，37(2)：392-397. Ren Jianwen，Li Sha，Yan Minmin，et al.Emergency control strategy for line overload based on power flow tracing algorithm[J].Power System Technology，2013，37(2)：392-397.

[13]陈珩.电力系统稳态分析[M].北京：中国电力出版社，2007.

[14]沈瑞寒，刘涤尘，赵洁，等.基于加权网络模型的电网潮流转移下危险线路识别[J].电网技术，2012，36(5)：245-250. Shen Ruihan，Liu Dichen，Zhao Jie，et al.Weighted network model based recognition of dangerous lines under power flow transferring[J].Power System Technology，2012，36(5)：245-250.

[15]苗世洪，马帅，尚亚男，等.基于割点和路径搜索的输电断面快速识别方法[J].电力系统自动化，2014，38(2)：39-45. Miao Shihong，Ma Shuai，Shang Yanan，et al.A fast recognition method of transmission section based on cut-vertex and path search[J].Automation of Electric Power Systems，2014，38(2)：39-45.

[16]杨文辉，毕天姝，薛安成，等.基于图论的潮流转移路径的快速搜索[J].电网技术，2012，36(4)：84-88. Yang Wenhui，Bi Tianshu，Xue Ancheng，et al.An approach for quickly searching power transferring paths based on graph theory[J].Power System Technology，2012，36(4)：84-88.

[17]郭志忠.电力网络解析论[M].北京：科学出版社，2008.

[18]杨文辉.预防连锁跳闸的关键线路后备保护与紧急控制策略研究[D].北京：华北电力大学，2012.

[19]程临燕，郝治国，张保会，等.基于内点法消除输电断面过载的实时控制算法[J].电力系统自动化，2011，35(17)：51-55. Cheng Linyan，Hao Zhiguo，Zhang Baohui，et al.Fast elimination of overload in transmission line section based on simplified primal-dual interior point method[J].Automation of Electric Power Systems，2011，35(17)：51-55.

[20]王凯.基于复杂网络理论的电网结构复杂性和脆弱性研究[D].武汉：华中科技大学，2011.

[21]鞠文云.基于复杂网络理论的电力系统脆弱元件辨识指标研究[D].武汉：华中科技大学，2013.

附 录

(A)

A Zone-divided Emergency Control Strategy for Overload Lines Based on Power Sensitivity

XuYanZhiJing

(State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources North China Electric Power University Baoding 071003 China)

To avoid removing the overload lines caused by power flow transferring，a zone-divided emergency control strategy for overload lines based on power sensitivity is put forward.Based on the current correlation coefficient matrix，the power sensitivity matrix between line power variables and nodal injection power variables is derived.The balance machine is introduced to the emergency control.Then the complex phasor calculation is simplified to real number calculation.The power system is divided into generalized power flow transferring zones according to the network topology.The nodes outside of the zone and the zone connecting cut point are proved to be with very closed power sensitivity for lines inside the zone.So the computational area can be simplified to the generalized power flow transferring zone to which the overload lines belong.With the combination of the local sensitivity calculation and the sparse vector techniques，the amount of calculation and memory are greatly reduced.The control node group is obtained by comprehensive sensitivity.Considering the redundant power of normal lines，the reverse equal amount adjustment method is used to determine the adjustment power amount，which avoids the tidal flow check and improves the emergency control speed.The validity and the superiority of the method are verified with IEEE39 and IEEE118 bus systems.

Power system，overload lines，power sensitivity，the generalized power flow transferring zone，local sensitivity calculation

附图1 IEEE118节点系统App.Fig.1 IEEE118 bus system

线路编号线路起点线路终点热稳定功率极限/MW线路编号线路起点线路终点热稳定功率极限/MW1109600915310029210010092542003941001009349501004100981009449511005100991009551521006101100100965253100710210110097(双回线)49541008921021009854531009100103200995455100101001041001005456100111031041001015655100121031056010250571001310410510010357561001410010610010451581001510510610010558561001610510710010659541001710610710010759551001810510880108(双回线)5956100191081091501095615020411100110605910021511100111615910022103110100112616020023109110100113626010024111110100114616210025110112100115646320026171131001166538250273211310011765642502832114100118(双回线)6649600291141151001196662100302711510012067621003168116250121666710032121171001226568100337511810012369471003411876100124694910035111210012567100361221001267024100

续附表1

国家自然科学基金(50777016)和中央高校基本科研业务费专项资金(NO.12MS110)资助项目。

2014-12-17 改稿日期2015-03-17

TM711

徐 岩 男，1976年生，博士，副教授，研究方向为电力系统保护与安全控制、新能源发电和智能电网。

郅 静 女，1990年生，硕士研究生，研究方向为电力系统保护与安全控制。(通信作者)